基于DNN 的OFDM 系统非线性失真补偿
2021-03-08刘步花
刘步花,丁 丹,杨 柳
(1.航天工程大学 研究生院,北京 101416;2.航天工程大学 电子与光学工程系,北京 101416)
0 引 言
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)能有效地抑制频率选择性衰落且具有较高的频谱利用率,在如今通信系统中有着重要的应用前景。高功率放大器(High Power Amplifier,HPA)是通信系统中不可缺少的组成部分,具有固有的非线性特性。OFDM 的多个独立子载波叠加造成信号峰均比较高,再经过HPA 放大,使信号造成严重的畸变,影响系统的误比特率(Bit Error Rate,BER)性能。
经典的线性化技术主要有反馈技术[1]、前馈技术[2]、预失真技术[3]等。它们的局限是需要精确获知射频前端的输入信号,但与发射端不同,接收前端的输入信号是很难获取的。实际研究时往往采用一种简单的“盲”线性化技术——功率回退法(Input Back⁃Off,IBO)[4],在确保接收前端效率的情况下,用此方法提高射频前端的线性度。机器学习(Machine Learning,ML)的本质是得到样本中输入与输出的映射关系,而深度神经网络(Deep Neural Network,DNN)作为 ML 的分支,同样具有拟合输入输出非线性关系的能力[5]。文献[6]运用了1 个隐含层和9 个神经元组成的前馈神经网络,设置了一个预失真,在一定程度上改善了传输质量,提高了系统的BER性能。文献[7]采用了一个双输入双输出的前向神经网络,包括1 个隐含层和9 个神经元,同时简化了更新神经网络权重的学习算法,该方法加快了收敛速度提升了系统的BER 性能。然而,此类非线性消除方法都是利用神经网络作为预失真器,而不是在接收端进行处理,同样存在数据获取的难题。
本文针对加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道下OFDM 系统的射频发送带来的非线性失真问题,提出一种基于DNN 的非线性时域补偿和频域补偿的方法,并讨论了时域补偿和频域补偿下DNN 不同的非线性拟合能力。在接收端对信号进行非线性补偿避免了传统算法和神经网络预失真法的数据获取难度,同时也提升了系统数据传输的准确率。
1 基于DNN 的OFDM 系统模型
1.1 非线性失真下的OFDM 系统
图1 是非线性失真下的OFDM 系统框图。发送端进行信号处理的过程是:首先进行正交相移键控(Quadrature Phase Shift Keying,QPSK)调制,然后进行逆傅里叶变换(Inverse Fast Fourier Transform,IFFT),再加入循环前缀(Cyclic Prefix,CP),最后射频放大发送数据,此时信号产生了非线性失真。接收端进行发送端的逆过程,首先去循环前缀,再进行FFT 变换和QPSK解调,最后判决得到比特流。由于是在AWGN 信道下仿真,所以在IFFT 变换之前不需要插入导频。HPA的输出信号表现为调幅⁃调幅(AM⁃AM)和调幅⁃调相(AM⁃PM)效应,采用无记忆非线性放大的Saleh 模型[8]的幅度和相位为:

式中:r(m)是信号的幅度;ϕ(m)是信号的相位;a1,b1,a2,b2为 Saleh 模 型 的 参 数 。
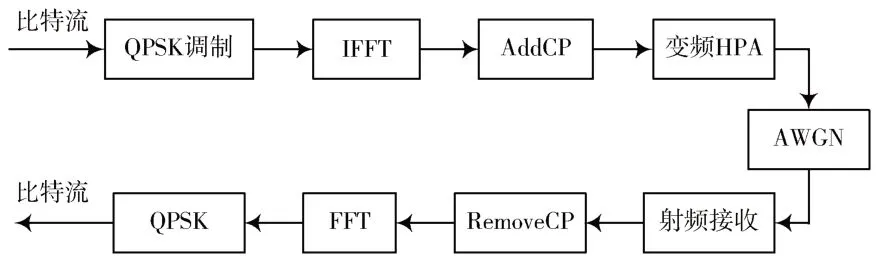
图1 非线性失真下的传统OFDM 系统
在传统OFDM 接收端加入DNN 的数据处理模块,即为本文设计的AWGN 信道下OFDM 系统接收机,图2,图3 是DNN 作为非线性补偿器的OFDM 系统接收端结构图。将其设计为二输入二输出的含两层隐含层的全连接网络,各层神经元个数为2,10,10,2,取名“Com⁃Net”。
1.2 DNN 模型训练和数据的产生
图4 为Com⁃Net 网络结构图,输入输出为复数信号的实部和虚部,各占一个神经元。Com⁃Net 作为不同的非线性补偿器时,输入样本和输入标签不一致。作为时域信道补偿器时,输入样本为OFDM 系统中接收端去CP 之后的信号,标签为OFDM 系统中加CP 之前的信号;作为频域信道补偿器时,输入样本为FFT 解调后的信号,输入标签来自于IFFT 变换之前的信号。

图2 DNN 时域补偿器
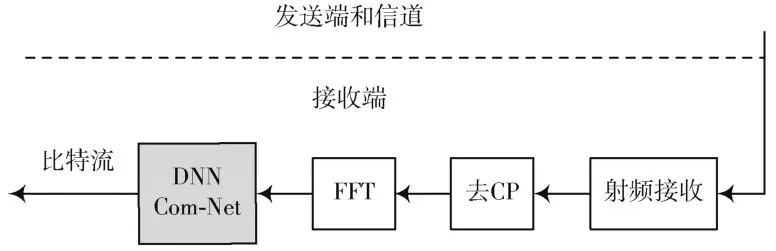
图3 DNN 频域补偿器

图4 Com⁃Net 结构图
发送端在每一次仿真时首先随机生成0,1 序列作为OFDM 系统的输入数据流,因为在AWGN 信道下仿真无需进行信道估计,不需要插入导频,所以设置OFDM一帧为两个数据符号,如图5 所示,每个符号长度为64。DNN 训练样本的数据生成如图6 所示,OFDM 参数设置和神经网络训练参数设置见表1。

图5 发送端OFDM 帧结构
2 仿真分析
2.1 非线性失真仿真分析
在AWGN 信道下进行仿真,放大器的非线性放大的参数有三组,代表三种非线性特性,图7为它们的AM⁃AM和 AM⁃PM 转换曲线。

图6 数据产生流程

表1 训练参数设置
第一组非线性参数[9]:
a1=2,b1=1,a2= π 6,b2=1
第二组非线性参数[8]:
a1=2.158 7,b1=1.1517,a2=4.003 3,b2=9.104 0
第三组非线性系数[8]:
a1=1.963 8,b1=0.994 5,a2=2.529 3,b2=2.816 8
三组非线性参数的AM⁃AM 转换(最大值归一化)曲线和 AM⁃PM 转换曲线如图 7 所示,以 AM⁃PM 相位变换来看,其中第一组非线性参数相位变换范围最小,最大值为15°;第二组非线性参数下相位变换最大值为22°;第三组非线性参数下相位变换最大为34°。
2.2 Com⁃Net 非线性补偿性能分析
图8~图10 为在三组非线性参数下,Com⁃Net 时域补偿和频域补偿的BER 性能比较。
从图8 可以看出,DNN 时域补偿器的性能与IBO=-2 dB 时接近,说明此非线性参数下Com⁃Net 时域补偿非线性可以避免2 dB 的功率损失,而DNN 频域补偿器性能未见明显优势。
从图9 来看,DNN 时域补偿器的性能与IBO=-6 dB时接近,DNN 频域补偿器的性能在信噪比低于20 dB 时优于IBO=-3 dB 时的性能,在20 dB 之后性能优势降低。说明在第二组非线性参数下,Com⁃Net 时域补偿器能避免6 dB 的功率损失,频域补偿时低信噪比下能避免3 dB 的功率损失。

图 7 AM⁃AM 和 AM⁃PM 非线性放大

图8 第一组非线性参数
从图10 来看,DNN 时域补偿器的性能与IBO=-6 dB 时接近,DNN 频域补偿器的性能优于IBO=-3 dB的性能,说明第三组非线性参数下,Com⁃Net 时域补偿非线性能避免6 dB 的功率损失,频域补偿非线性能避免3 dB 的功率损失。
综上可以得出,Com⁃Net 具有可观的非线性拟合能力,且能避免一定程度的输入功率损失。
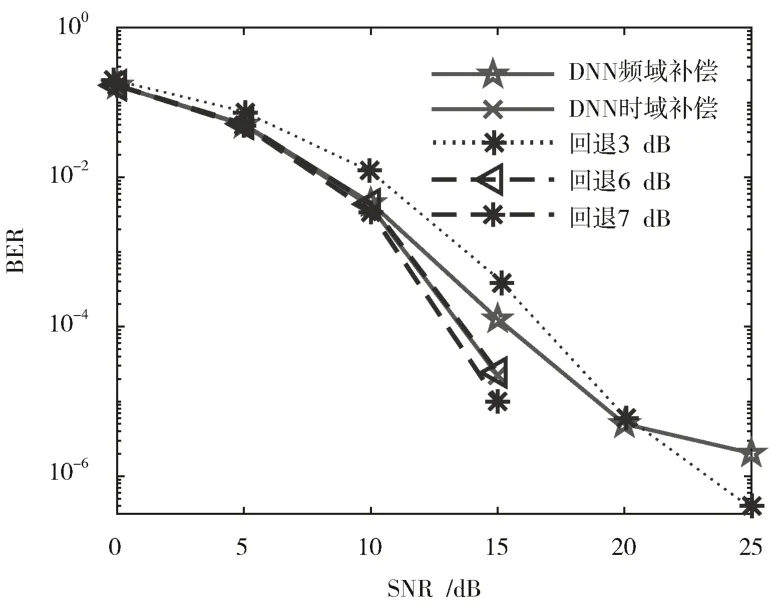
图9 第二组非线性参数
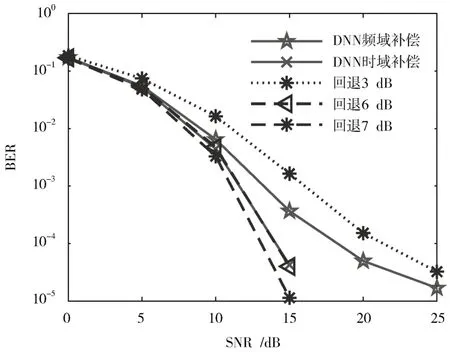
图10 第三组非线性参数
由图8 结合图7 非线性特性分析可知:图7a)中,在第一组非线性参数下,DNN 时域补偿器只能避免2 dB的功率损失,DNN 非线性拟合的性能优势不明显;从图7b)和图7c)可知,第二组和第三组非线性特性相位失真比第一组严重,而此时Com⁃Net 时域补偿可以避免6 dB 的功率损失。说明随着非线性AM⁃AM 和AM⁃PM强度的加深,DNN 拟合的性能优势逐渐显现。
此外,从图8~图10 仿真结果可以看出DNN 时域频域补偿的训练样本来自于加CP 和去CP 之间,少了频域补偿时的 IFFT 和 FFT 的数据转换步骤,Com⁃Net 只需要始终优于DNN 频域补偿。从数据生成来看,Com⁃Net 拟合放大器的非线性失真,省略拟合IFFT 和FFT 变换的非线性函数的工作量,所以在同样的神经网络结构和训练超参数下,Com⁃Net 时域补偿器的BER 性能优于频域补偿器的BER 性能。因此,神经网络将通信系统数据处理模块模拟成一个“黑盒”[5],“黑盒”越大,要获得足够的性能优势,就越需要找到合适神经网络结构去拟合这个“黑盒”。
3 结 语
本文针对AWGN 信道下射频发送时放大器导致的非线性失真问题,利用双输入双输出的深度神经网络将非线性补偿放在接收端,避免了射频发送端的数据获取的难度和非线性功率回退时带来的功率损失。同时,从Com⁃Net 时域补偿优于频域补偿角度来看,对于不同的输入与输出数据,要找到合适的网络结构和网络参数,才能发挥神经网络非线性拟合能力,将“黑盒”透明化。
