钢筋混凝土空心剪力墙体系抗震性能分析

张朴睿，关群 （合肥工业大学土木与水利工程学院，安徽 合肥 230009）

0 前言

随着近现代工业技术的不断发展，人们对于建筑物的模式、种类、风格提出了更多样、复杂的要求。低碳、环保、节能的理念成为许多行业，尤其是建筑行业的追求目标。混凝土空心剪力墙体系就是在这样的背景下被提出的一种新型剪力墙体系。

混凝土空心剪力墙是指将典型的钢筋混凝土剪力墙内部的部分混凝土挖除一部分，形成竖向空心孔洞，从而达到减轻结构自重、减小地震效应与结构刚度、增强结构抗震性能的一种剪力墙结构形式；同时其内部形成密闭的空气层，还能达到良好的保温隔热效果。

针对各类空心剪力墙体系，目前已有大量学者对此开展了研究。杨永哲等对四片不同轴压比不同、剪跨比的空心剪力墙试件进行低周往复加载试验，并通过ANSYS有限元软件对试验过程进行模拟，其结果表明与实心剪力墙体系相比，空心剪力墙体系承载力以及刚度均有所下降，但空心剪力墙后期刚度更加稳定。彭博等介绍了一组适用于低层建筑的装配式圆孔剪力墙结构，对其进行受力性能影响因素分析，其结果表明剪跨比和轴压比对圆孔剪力墙力学性能影响较大，与实心剪力墙相比，圆孔剪力墙结构自振周期长、层间剪力小、刚度小、层间位移大，整体抗震性能良好。王琼梅等对空心剪力墙进行了缩尺的拟动力试验研宄，研宄表明空心剪力墙结构在水平地震作用下具有较高的抗震能力，且具有较好的延性。

基于此，本文提出了一组开孔形式为四块矩形孔的钢筋混凝土空心剪力墙体系，运用ABAQUS有限元软件进行滞回模拟，通过对模拟结果的分析，探究方孔空心剪力墙与实心剪力墙的抗震性能对比，以及开孔率对于混凝土空心剪力墙力学性能的影响。

1 有限元模型的建立

1.1 混凝土材料本构关系

本研究中混凝土的本构关系模型曲线采用Hognestad建议的公式，曲线的上升段为二次抛物线，下降段为斜直线，曲线方程式如式（1）（2）所示，应力应变曲线如图1所示。混凝土受拉应力应变关系采用上升段斜直线接下降段斜直线的模型，应力应变曲线如图2所示。

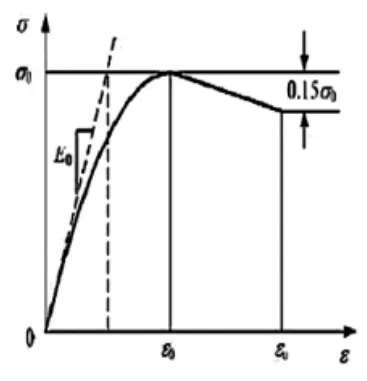
图1 混凝土受压应力-应变曲线

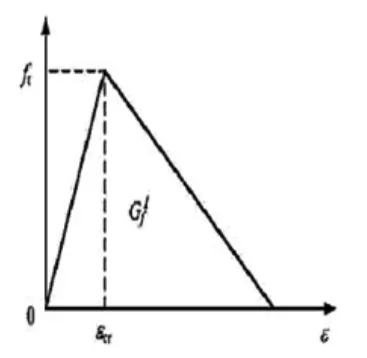
图2 混凝土受拉应力应变曲线

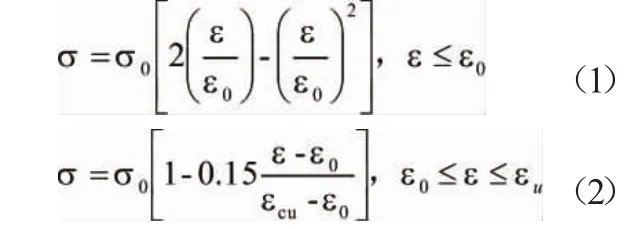
式中：σ，ε分别表示混凝土的应力、应变；σ，ε分别表示混凝土峰值应力及峰值应变，ε为混凝土的极限压应变。取值：ε=0.002，ε=0.0038。

本文选取ABAQUS软件中自带的混凝土塑性损伤模型，该模型需要用户依次输入膨胀角、偏心率、双轴极限抗压强度与单轴极限抗压强度之比（f/f）、第二应力不变量在拉伸子午线上取值与在压缩子午线是取值的比值（K）、粘性系数，由参考文献 [5]分别取为30、0.1、1.16、0.667、0.001。

1.2 钢筋本构关系

考虑到试件在低周水平反复加载下达到屈服点之前，近似于理想弹性体，因此在模拟中钢筋本构关系选用描述弹塑性的双斜线模型，其应力-应变表达式为：

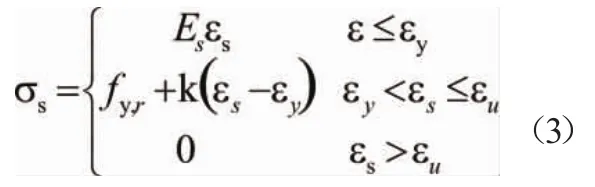
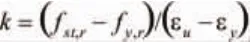
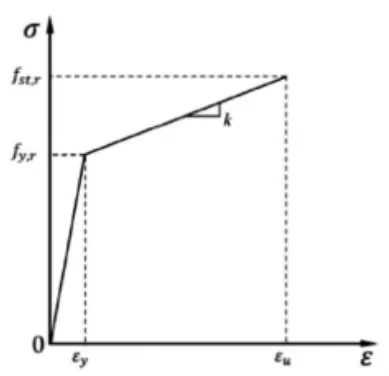
图3 钢筋的应力应变双斜线模型

1.3 模型算例

为了验证本文本构关系选取的适用性及参数的有效性，选用文献[6]中实心剪力墙构件SW-1进行非线性模拟。

文献[6]试验的剪力墙构件SW-1配筋及尺寸如图4所示。剪力墙截面为一字型，剪力墙两端设置约束边缘的暗柱构件，墙体厚度为140mm，宽度为1650mm，高度为2600m；边缘暗柱尺寸为200mm×140mm下部地梁截面为400mm×450mm，每侧延伸出墙板外侧600mm；加载梁的截面尺寸为250mm×400mm，长度与墙体相同，为1650mm。墙体中所有钢筋均为HRB400级钢筋，水平及竖向钢筋间距均为600mm，轴压比为0.2。

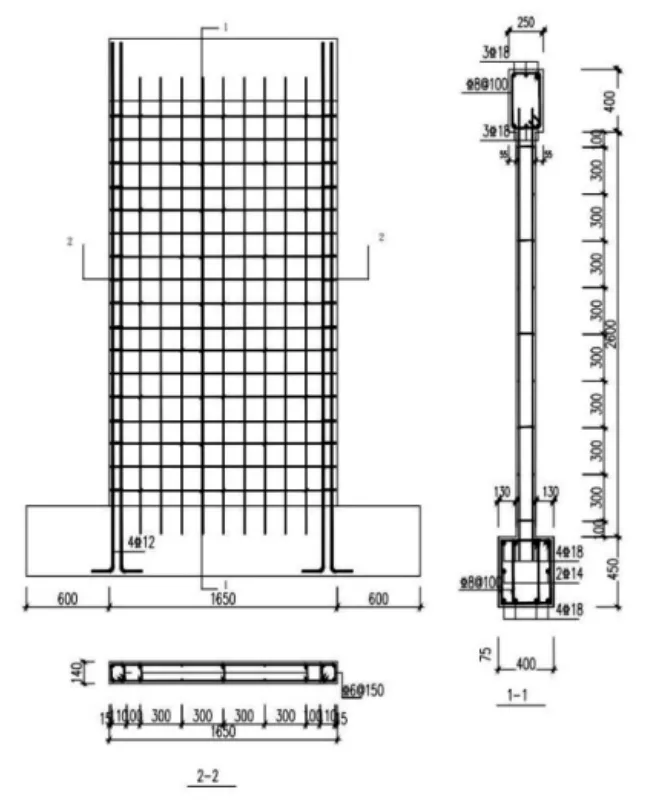
图4 SW-1试件尺寸及配筋

试件分析结果对比如图5，数值模拟计算结果表明，所选取的钢筋和混凝土本构关系以及建立的模型尚能较好地刻画试件的受力变形特征，对剪力墙在反复荷载作用下的力学性能模拟精度较高。

图5 SW-1数值计算结果与试验结果对比

2 空心剪力墙体系数值模拟

2.1 分析模型试件

为对自重更轻、抗震性能更优、保温性能更良好的钢筋混凝土空心剪力墙进行进一步研究，基于文献[6]设计了三片不同孔洞率的混凝土空心剪力墙。三片剪力墙模型的尺寸及配筋均与SW-1相同，编号分别为 S-1、S-2、S-3。模型中混凝土均选用C30级混凝土，弹性模量E=3×10MPa，泊松比 μ=0.2。模型中选取钢筋的墙体截面尺寸见表1，截面配筋图见图6。

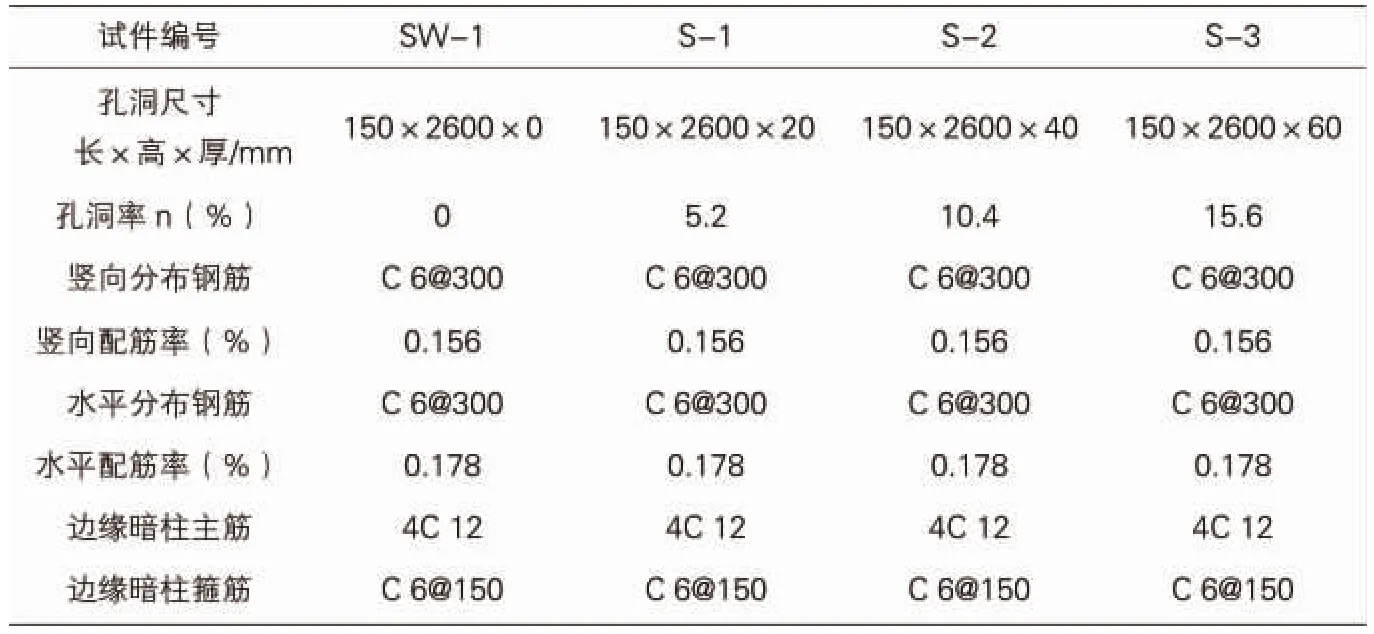
试件参数 表1

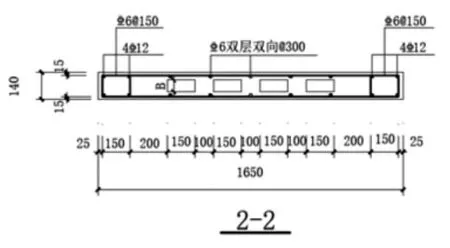
图6 S-1～S-3空心剪力墙截面配筋图

在此配筋基础上，利用ABAQUS有限元软件，通过低周反复加载的方式来模拟地震荷载，以假定的第一振型为基础，将低周反复循环作用下的位移或荷载施加给研究对象，结构自身周期远小于每次加载的周期。水平位移反复加载曲线如图7所示。

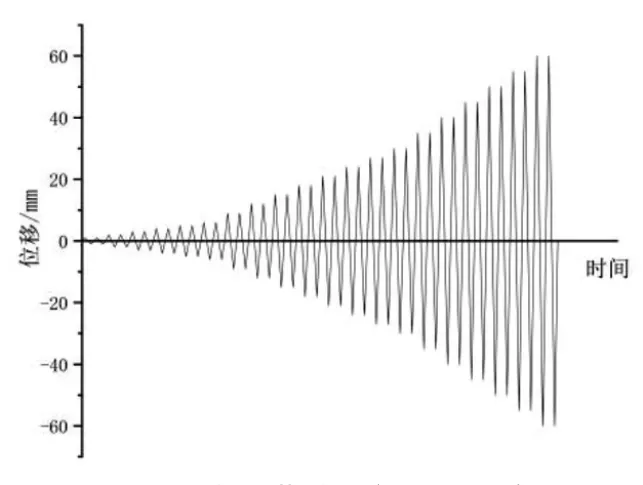
图7 水平荷载反复加载制度

2.2 荷载位移曲线

在低周反复加载试验中，以构件水平反力和位移为变量，绘制的荷载-位移曲线能有效地反映构件在模拟地震荷载的作用下不同阶段的变形性能。

空心剪力墙构件荷载-位移曲线如图8所示，可以看出，与实心剪力墙相比，空心剪力墙的极限承载力随着孔洞率的增加略微下降，但从荷载峰值到极限位移所经历的过程可以看出，空心剪力墙结构具有更强的抗变形能力。

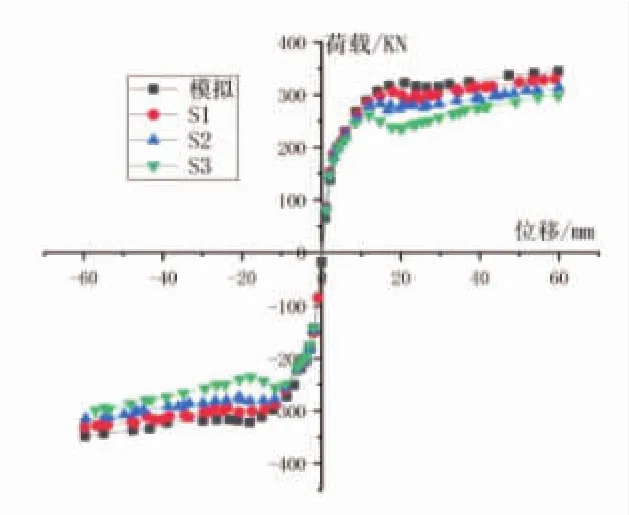
图8 荷载-位移曲线对比

2.3 延性性能

延性是指结构从屈服到破坏这一阶段的变形能力，发生延性破坏时结构达到最大承载力，随着荷载继续作用，其承载力缓慢降低并伴随着较大变形，具有可预见性。

本文采用位移延性系数μ来衡量试件的延性，按式（4）来计算：

式中：Δ为试件的极限位移；Δ为试件的屈服位移。

根据骨架曲线结合“R.Park”法确定结构屈服点，计算的位移延性系数见表2。

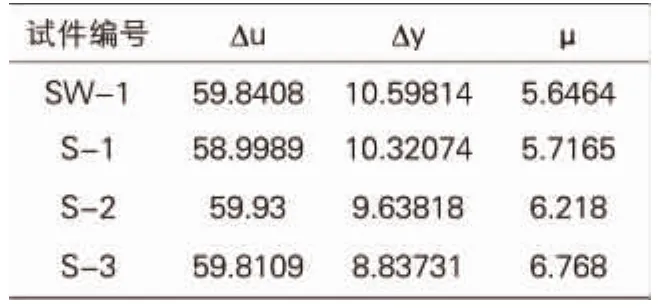
位移延性系数对比 表2

由表2可以看出，相对于实心剪力墙，混凝土空心剪力墙具有更好的延性，S-1、S-2与 S-3的位移延性系数较SW-1都有所提高。而随着空心剪力墙孔洞率的增加，结构的延性性能进一步提高。

3 不同轴压比下空心剪力墙骨架曲线及延性对比

轴压比是影响剪力墙抗震性能的主要因素之一。基于以上分析，拟选用空心剪力墙S-1为标准构件，进行不同轴压比作用下的力学性能模拟，得出试件的延性性能和骨架曲线变化趋势如表4和图9所示。

由表3以及图9可以看出，随着荷载的增大，模型的刚度退化现象并不明显。试件轴压比从0.1增大至0.4的过程中，结构极限承载力逐渐提升，但位移延性系数也随之降低。说明随着轴压比的增大，结构更显“脆性”，因此在进行结构设计时，应合理控制轴压比参数。

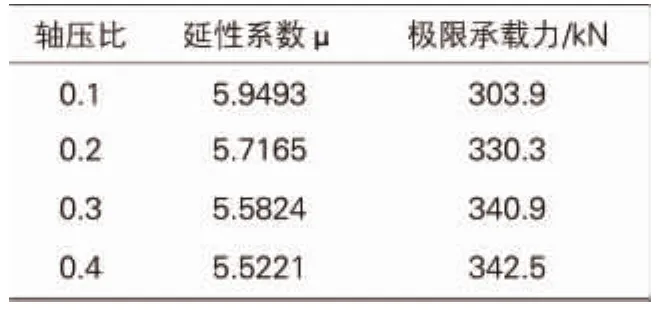
不同轴压比下构件延性及承载力 表3

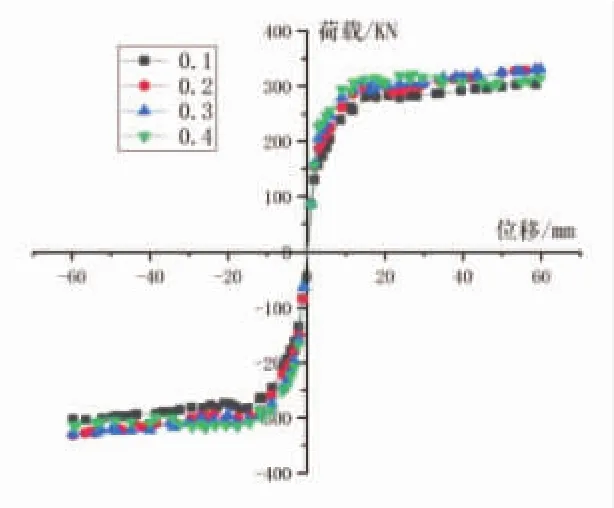
图9 不同轴压比下荷载-位移曲线对比

4 结论

通过ABAQUS有限元软件对混凝土空心剪力墙抗震性能的数值模拟，建立了本构单元模型，分别赋予钢筋和混凝土合理的本构参数。通过与现有试验的对比，验证了模型的适用性，并对空心剪力墙在孔洞率不同的情况下以及轴压比不同的情况下的抗震性能进行了研究分析，结果表明：

①在ABAQUS中，选择的混凝土塑性损伤模型和钢筋的双折线模型，得出计算结果尚能较好地模拟试验结果，说明选择的材料本构关系能较好地模拟混凝土空心剪力墙的抗震性能；

②通过对不同孔洞率剪力墙的模拟及与文献[6]对比可以得出，在剪力墙中配置空心孔洞能够有效提高剪力墙的承载能力，并且通过各模型的骨架曲线来看，配置竖向空心孔洞也可以提高结构的延性，使结构具有更好的抗震能力；

③轴压比对结构的极限承载力有着较为显著的影响，随着轴压比的增大，空心剪力墙承载力均不断提升，但其延性却有所下降。在轴压比从0.1增加到0.3的过程中，延性系数衰减较快，而从0.3增加到0.4的过程中衰减变慢。综上，在进行结构设计时，应通过结构轴压比进行合理控制，保证结构的抗震性能。