自适应平方根球型卡尔曼滤波下的SOC估计

刘 楠，叶望博，李 明，吕 甜，张雪霞

(1.中车唐山机车车辆有限公司，河北唐山063000；2.西南交通大学唐山研究生院，河北唐山063000)

锂电池荷电状态(SOC)的估算对于电池管理系统而言，是至关重要的一环。电池的SOC 代表锂电池当前剩余容量。在有轨电车运行过程中，锂电池作为一种电动机供能装置，具有很高的能量密度，并且锂电池的当前状态与有轨电车的运行方式密切相关。因此，对锂电池的SOC 进行估算，能较好地反映锂电池当前剩余容量，从而预测有轨电车的运行状态。

当前对锂电池SOC 估算的方法主要包括安时积分法，开路电压法，卡尔曼滤波法(KF)以及人工神经网络法，深度学习等等[1-4]。其中安时积分法较为依靠SOC 初值的准确性，以及电流测量的精度，容易产生累计误差。而开路电压法，其开路电压的获取方法需静置电池较长时间，无法实时获取。人工神经网络法则要求庞大的关于锂电池SOC 的数据，包含各种状况下SOC 的变化状况，因此不太实用。针对锂电池这种非线性系统而言，无迹卡尔曼滤波方法[5]常被用于锂电池SOC 的估算，其计算速度以及精度均能达到较好的效果。

本文以2.7 V/20 Ah 的钛酸锂电池作为研究对象，通过实验及仿真验证，并分析其工作特性，最终建立了一阶Thenevin等效模型。此模型的计算量较少，且精度较高，能够很好地反映锂电池的工作特性。利用MATLAB 对等效模型的各个元件参数进行辨识。最后，针对标准UT 变换中设定参数较多且难以确定，以及因噪声统计特性未知而造成估算精度下降的两个问题，本文提出了在传统平方根无迹卡尔曼滤波方法下做球形变换，加入噪声自适应因子[6-8]的估算方法，对锂电池SOC 进行估算，提升了其估算的准确性和鲁棒性，使估算的误差不超过1%。

1 锂电池等效模型及参数辨识

1.1 等效模型

为模拟电池充放电特性，需对锂电池进行等效电路建模。通过不断地测试仿真，考虑到SOC 估算的准确性及计算量，本文采用一阶Thenevin 电路模型[9]作为钛酸锂电池的等效模型。此模型由三个部分组成：(1)电压源Uoc；(2)欧姆内阻R0；(3)极化内阻Rp和极化电容Cp组成的并联部分，见图1。

图1 一阶Thenevin模型

图1 中，极化部分可模拟锂电池的极化效应，而在充放电时，电压骤变过程的瞬态反应可由R0表示。通过基尔霍夫定律，得该模型电路方程式：

式中：UL为电池端电压；I 为总电流，以电池放电方向为正；Up为极化模块两端电压。

利用安时积分法，可得锂电池SOC 计算式：

式中：η 为库仑效率；Qa为锂电池标称容量。

1.2 参数辨识

锂电池等效模型的参数辨识主要包括4 个部分：开路电压Uoc，欧姆内阻R0，极化内阻Rp以及极化电容Cp。辨识的步骤为，将锂电池SOC 从100%到0%分成20 等份，每隔5%，均对锂电池进行一次HPPC 循环脉冲实验[10]，从而获得锂电池电压变化曲线，如图2。通过式(3)～(7)可辨识出不同SOC 值下的参数值。

图2 HPPC实验曲线图

锂电池在静置一段时间后，电压值会逐渐趋于稳定状态，此时电压即电池的开路电压值。因此，根据不同SOC 状态下所得到开路电压值，利用多项式拟合，可得OCV-SOC 之间的关系见式(3)：

极化模块的辨识方法，则可根据电池在静置时间段内，所发生零状态响应得出：

通过MATLAB 中cftool 工具箱，利用最小二乘法，输入每个SOC 点所对应的Ut，Uoc，It，R0值，可得到对应的极化内阻Rp以及时间常数τ 的值。最后，与开路电压拟合方法一样，利用多项式拟合，将R0，Rp，Cp均拟合成关于SOC 的7 次多项式，见式(6)～(7)：

式中：内阻均为mΩ级，极化电容为kF 级。

1.3 模型验证

利用等效电路模型以及参数辨识的结果，在MATLAB/Simulink 软件中搭建一阶仿真电路。选取脉冲充放电测试实验验证模型的可行性。

以脉冲充放电实验为例，以3 C 倍率对电池放电10 s，静置40 s，然后以3 C 倍率充电10 s，静置40 s，再以1 C 倍率放电3 min，直至放电到截止电压，其仿真电压曲线与实验电压曲线进行对比，见图3(a)。从图中可看出仿真端电压与实际端电压的区别很小，可以反映出电池在工作时电压的变化情况。由图3(b)误差曲线可知，前中期模型仿真效果最好。随着容量逐渐减少，即在后期时，其模型仿真值与实际值的差别较大，但最大误差仍未超过0.15 V，误差较小。因此表明，一阶RC 模型满足要求，为SOC 的估算提供了基础。

图3 脉冲充放电下电压对比图

2 锂电池SOC 的估计算法

2.1 平方根无迹卡尔曼滤波算法(SRUKF)

SRUKF 是在传统UKF 的基础上，运用协方差矩阵的平方根取缔原有的协方差矩阵参与到迭代的过程，通过QR 分解以及Cholesky 一阶更新获取协方差平方根，保证协方差矩阵的半正定性，并且此举能够提高其算法的精度。

SRUKF 的具体步骤如下：

(1)对状态变量的均值xˉ0和协方差矩阵平方根S0进行初始化操作：

(2)对k-1 时刻的状态变量进行sigma 化：

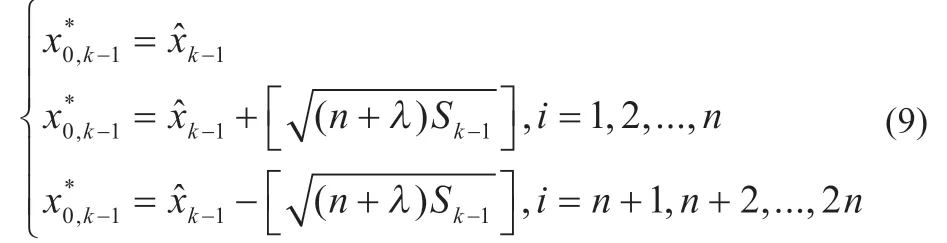
Sigma 化即将一个n 维的状态变量，利用对称采样取点的方法，得到2n+1 个与初始状态变量相同的统计特性。并且每个Sigma 点具有不同的权重系数，其权重值计算方法如下：

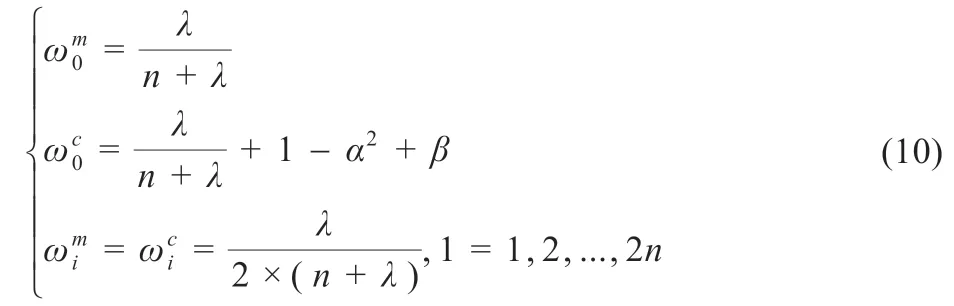
式中:λ 为缩放尺度因子，λ=α2(n+k)-n；n 为维数；α 为sigma 点以均值xˉ0为中心所分布的范围大小，一般取范围在10-6～1 之间的值；β 能够减小高次项所造成的影响，一般取β=2；k 即辅助尺度参数，一般k+n≠0。适度改变α 以及k 的值可以提高估算的准确性。

(3)时间更新

利用xk-1与uk的值，利用状态方程式对xk进行预测，首先对sigma 点进行更新，得：

依照sigma 点的预测对状态变量的误差协方差矩阵采取QR 分解，并利用Cholesky 分解保证误差协方差矩阵的半正定性，从而消除由α 或k 的取值差异所导致权值系数出现负值的情况。Sx,k表征状态变量协方差矩阵的平方根，其k 时刻具体更新方程如式(13)：

(4)量测更新

(5)状态更新

卡尔曼增益的精确性会直接影响SOC 的估算准确度，而影响卡尔曼增益的因素主要是状态变量和观测量的互协方差，其计算方法为：

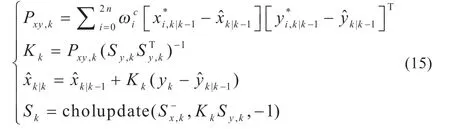
式中：Kk为卡尔曼增益；yk为k 时刻下所测得的端电压值；Sk即误差协方差的平方根。

2.2 球形UT 变换

在上述SRUKF 算法中，其UT 变换的权值计算包含过多需要设定的参数，例如α，β，k等。并且其参数的设定对最后估算结果会产生较大的影响，所以，在调整参数的环节，需要根据经验进行不断的尝试后，才有可能获得更好的结果。而这个调节的步骤一般较为复杂，为避免调整参数过程的繁复性，故选择球型UT 变换方法。球型UT 变换可将sigma 点从2n+1个点降至为n+2个点，从而减小了计算量。具体步骤如下：

(1)确定权值系数：

式中：ωi既表示状态变量均值的权值系数，也表示协方差矩阵的权值系数，且ω0通常取0。

(2)sigma 化：

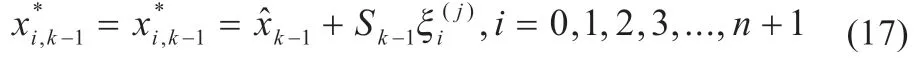
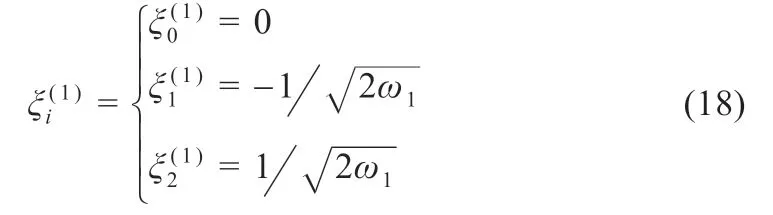
若j=2,3,4,…,n 时，对ξ(1)

i 则可知：

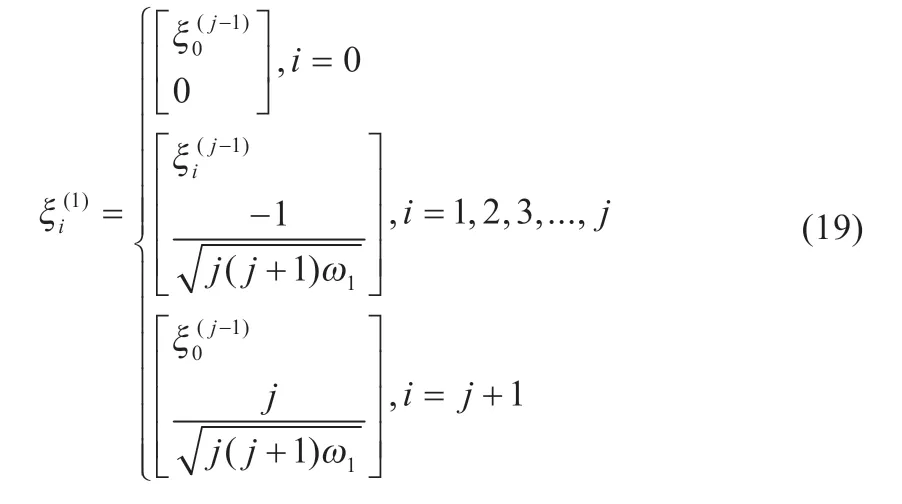
利用球形UT 变换则可替代传统SRUKF 中sigma 点的选取方式，简化计算量。

2.3 噪声自适应

在实际的工作状态中，无论在计算过程或是测量过程都会带来难以估计的噪声，并且这些噪声的实际分布极难获取。因此，在一般的操作过程都会将噪声的协方差矩阵设置为一定值，方便计算。但是，若取得的协方差矩阵不准确，则会导致精度问题，严重时会使迭代发散。对此，本文引入自适应因子，对噪声的协方差自行进行匹配，并不断更新协方差的值。

计算自适应调节因子矩阵Dk如下：

其中：

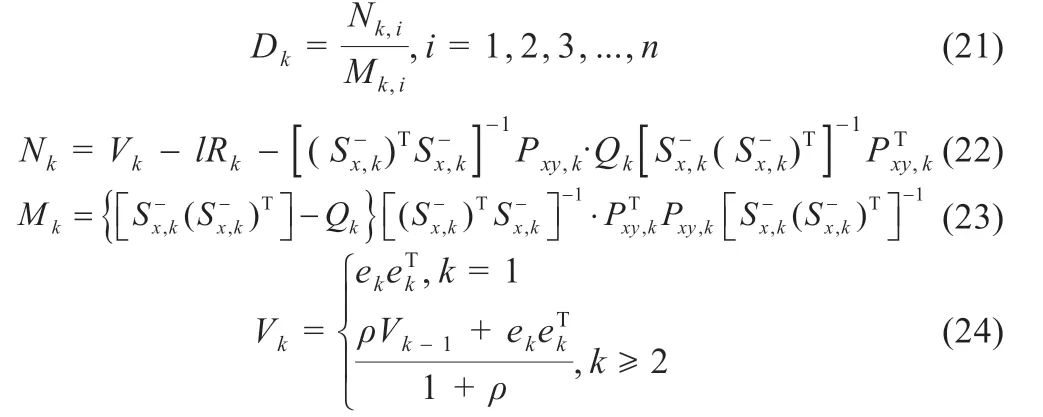
式中:ek为观测误差，即ek= yk- ŷk|k-1。

在引入自适应调节因子后，则式(17)可改写为：

3 仿真分析

验证平方根球型无迹卡尔曼滤波方法对锂电池SOC 估计的准确性。本文以2.7 V/20 Ah 规格的钛酸锂电池作为研究对象，其截至电压在1.8 V。在标准条件下分别进行不同的工况测试，主要包括恒流充放，HPPC 充放电测试。并通过EKF，传统SRUKF 与ASRUKF 进行仿真结果对比。

首先，为检验算法的鲁棒性，分别设置SOC 初始值为1，0.8 和0.1 三种情况下的算法收敛程度，如图4 所示。在放电初期，由于初始噪声的设定可能与实际噪声差别太大，导致算法的震荡较为严重，但很快趋于稳定，并收敛到可接受的误差范围内。在放电平台区，算法对SOC 的估算基本与实际理论值重合，并一直到放电终止。

图4 SOC初值在不同状态下估算结果图

由图4 可见，当设定的SOC 初始值与真实值较为接近时，收敛的时间较短，其最大估计误差不超过2%，而放电平台区至放电结束，其误差在0.7%左右。这是由于电流较为稳定，对算法干扰较少，因此算法具有很好的效果。且即使SOC 初始值设置偏离实际值，但算法依然能够很快地收敛到真实值附近，并保持稳定的跟随。这说明，该算法具有很好的滤波作用，且具有较强的鲁棒性，对锂电池SOC 估算效果很好。

图5(a)为3 C 恒流放电下，SOC 理论值与EKF，SRUKF，以及ASRUKF 的估计值对比。图5(b)则为误差曲线图。由图5 可知，EKF 的效果最差，误差在5%左右，SRUKF 的效果在后期也逐渐变差，误差在不断增大，最大误差为2.5%。而ASRUKF 方法的估计值最接近理论值，其误差基本维持在1%左右。因此，ASRUKF 的精度较之其余两种方法更佳。

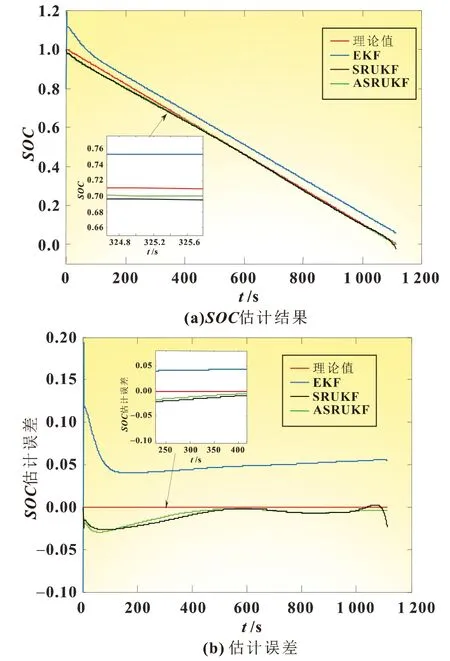
图5 恒流放电下SOC估计结果对比

根据图6 HPPC 测试条件下SOC 估算结果及误差对比，其具体操作流程可见前文参数辨识。由图可见传统SRUKF

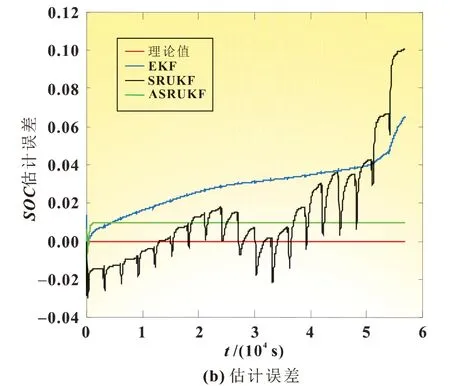
图6 HPPC 测试下SOC估计结果对比

在后期误差明显增大，且波动较为明显，而EKF 虽在后期误差也不断增大，但其波动幅度比SRUKF 算法小。经过自适应处理后的ASRUKF 算法，基本在测试1 000 s 之内，算法趋于稳定状态，误差始终保持在1%之内，算法稳定性很高。

4 结论

通过实验仿真说明，一阶Thenevin 模型能够满足本文所用钛酸锂电池的等效模型要求。并且，自适应平方根球型卡尔曼滤波方法相较于传统的SRUKF 方法而言，添加了自适应因子后，提高了SOC 的估算精度以及鲁棒性，即使在极为复杂的工况下，仍能使其最大误差不超过1%，且收敛速度较快，无论SOC 初始值偏离多少，能够很快收敛到真实值周围，滤波效果不错。