砂土中裙式吸力基础复合承载特性数值模拟
2021-03-07张雨坤王冲冲李大勇亓义菘
张雨坤, 王冲冲, 李大勇,2*, 亓义菘
(1.山东科技大学, 山东省土木工程防灾减灾重点实验室, 青岛 266590;2.福州大学土木工程学院, 福州 350108)
风能相对于其他能源形式来说,具有相对清洁而且可再生的优点。目前人们主要利用风能进行陆地风力发电和海上风力发电。与陆上风电相比较可知,海上风力发电具有资源丰富、占用陆地资源少、无噪音和视觉影响等特点[1]。1985年,丹麦建成了世界第一座海上风电场[2]。截至2018年,全球海上风电装机容量达22 GW。中国能够开发利用的海上风电约750 GW。然而,截至2018年,中国累计建设海上风电容量仅为3.63 GW。海上风力发电在中国有着广阔的发展前景。海上风电基础在服役过程中,主要承受的荷载是上部风机结构向下传递的竖向荷载以及海上因风、波浪等导致的竖向荷载和弯矩作用。这些荷载往往同时作用于风电基础,导致基础的承载特性非常复杂。截至目前,海上风电基础有多种形式,分别是:重力式基础、单桩基础、多桩基础和吸力基础。吸力基础是一种类似桶形的基础,它上部是封闭的、下部是敞开的,由于其具有承载性能好、造价低、可回收利用等优点已逐渐引起了人们的关注,并成功作为海上风力发电工程的基础得以应用[3-4]。丹麦分别于2002、2009年建成滩海风电机组和海上测风塔的基础[5]。2010年6月29日,中国在道达海上风电研究院建成的海上测风塔,所选用的基础形式都是吸力桶基础。
目前,中外学者针对吸力基础在不同土质和不同加载条件下的承载力进行了研究。武科等[6-7]采用极限分析中的上限法,建立了吸力桶基础承载力分析的上限极限分析模型,发现横向各向异性、不排水抗剪强度、基础的长径比是影响其竖向承载力的主要因素。Hung等[8]通过分析发现,长径比越大吸力基础的水平及竖向承载力越大,并提出了计算水平及竖向承载力的公式。Zhan等[9]通过采用数值模拟的方法,研究了不同长径比、不同偏心率等工况下吸力基础受竖向荷载、水平荷载以及扭矩荷载单独作用和组合作用时的承载性能。Monajemi等[10]通过开展数值模拟,将吸力基础受倾斜荷载时的受力状况转换为受组合荷载作用,研究发现当不排水抗剪强度越大时V-M和H-M包络线范围越大(V、H、M分别为竖向、水平、弯矩荷载)。Byrne[11]通过采用数值模拟和理论分析的方法,研究了不同方向长期循环荷载之间的相互影响关系,得到了吸力基础二维及三维破坏包络面,并拟合了相关参数。Zhong等[12]针对传统吸力基础和内部具有十字形壁舱的新型吸力基础,采用数值模拟的方法研究了其在单调荷载和组合荷载作用下的承载性能,得到了H-M破坏包络线。Gourvenec等[13]开展数值模拟,通过对不排水极限状态下均质和非均质地基中不同长径比的研究,得出了其在复合荷载作用下的承载力规律,同时绘制出了基础破坏包络面,提出了计算吸力基础在组合荷载作用下极限承载力的方法。

图1 裙式吸力基础Fig.1 Modified suction caisson
综上所述,目前中外的学者对于吸力基础的研究主要侧重在不同土质和不同加载条件下的承载力。然而对于吸力基础在砂土中的复合加载条件下的承载性能的研究较少。为了对现有传统吸力基础进一步改进,李大勇等[1]提出了一种新的吸力基础形式——裙式吸力基础,如图1所示。裙式吸力基础是在传统吸力基础之上增加了裙结构。研究表明裙式吸力基础在砂土中有较好的沉贯性[14-15];裙结构的增加能够有效地提高基础的承载能力和限制基础的侧移[16-22];在使用同样用钢量和单调荷载作用下,裙式吸力基础的水平承载力比传统吸力基础要高,大约提高28.6%[17]。但是前人研究仅是在单调加载条件下得出的结论,而对裙式吸力基础复合加载条件下承载力的研究尚鲜见报道。
开展数值模拟,分别对裙式吸力基础在V-M、H-M、V-H-M等复合加载条件下的承载性能进行研究,分析吸力基础周围土体的变形规律,得出吸力基础的破坏包络线,同时研究裙式吸力基础与传统吸力基础承载特性的区别,以供工程实践借鉴。
1 有限元模型
采用刚体对吸力基础进行模拟,其参数参考文献[18]。“裙结构”尺寸大小对吸力基础的承载特性有很大的影响,为了研究这一特性,建立4种不同“裙结构”尺寸的裙式吸力基础模型。不同工况下吸力基础的尺寸如表1所示,砂土地基采用摩尔-库伦弹塑性模型,利用吸力基础数值模拟结果与模型试验结果反演出土体参数,吸力基础及土体参数如表2所示。
考虑到吸力基础结构的几何形状,同时为了降低计算成本,取土体与吸力基础的1/2进行有限元数值分析。为消除边界效应,结合课题组取得的研究成果,土体计算范围如下:水平方向选取15倍的主桶直径(15D1),竖直方向选取6倍的基础高度(6H1),如图2所示。

表1 吸力基础模型尺寸Table 1 Dimensions of suction caissons

表2 材料参数设置Table 2 Parameters used in FEM
为更准确得到破坏包络线,采用改进的Swipe加载法,如图3所示。位移和位移作用点位于桶体轴线顶部参考点O上,如图4所示,并规定如图4所示的运动方向为正向。
以桶直径120 mm,桶高240 mm的传统吸力基础为参照对象,分别进行加载高度和桶径之比为1.5、2的两种工况(即工况A、工况B)的承载力数值比较,比较数值模拟和试验结果,如图5所示,二者误差较小,数值模拟结果可靠。

图2 裙式吸力基础有限元模型Fig.2 Finite element model for modified suction caisson

图3 Swipe加载试验法Fig.3 Loading procedure of swipe test

u、w、θ分别表示水平、竖向和转角位移图4 作用在桶形基础上的荷载和位移Fig.4 Loads and resulting displacements of suction caisson

图5 吸力基础水平荷载与水平位移的有限元和试验结果Fig.5 Results between the finite element method and experiment for suction caisson
2 计算结果分析
2.1 V-H、V-M、H-M二维复合荷载作用下的结果分析
图6分别为相应复合荷载(V-H、V-M、H-M)作用下所得到的二维复合荷载无量纲化破坏包络线(γ′为饱和砂土的有效重度)。通过比较分析可以发现,相比较而言,裙式吸力基础包络线范围较大,传统吸力基础包络线范围较小。由图6(a)可知,裙式吸力基础有更大的竖向-水平组合承载力,裙宽裙高越大其破坏包络线包含的范围越大。分别比较工况2与工况3、工况2与工况4可知,裙宽对破坏包络线的影响大于裙高对破坏包络线的影响。由图6(b)可知,裙式吸力基础能承担更大的竖向-弯矩组合荷载的作用,比较不同尺寸的裙式吸力基础破坏包络线发现,裙宽裙高越大其破坏包络线包含的范围越大。由图6(c)可知,裙式吸力基础能承受更大的水平-弯矩组合荷载的作用,比较不同裙式吸力基础的破坏包络线发现,裙宽、裙高越大,破坏包络线的范围越大,进一步说明了“裙结构”的设置对提高吸力基础的承载力有积极影响。

图6 V-H、V-M、H-M荷载下承载力无量纲破坏包络线Fig.6 V-H,V-M and H-M normalized failure envelope
图7分别为相应复合荷载(V-H、V-M、H-M)作用下所得到的二维复合荷载承载力归一化破坏包络线。由图7(a)可知,不同裙式吸力基础的破坏包络线变化规律类似,裙宽裙高的改变对破坏包络线的变化影响较小。由图7(b)可知,在0≤V/Vult≤0.4范围内(下标“ult”表示极限承载力),破坏包络线斜率近似为零,即竖向荷载的变化对弯矩承载力的影响很小;在0≤M/Mult≤0.5范围内,破坏包络线斜率近似于无穷大,即弯矩荷载的改变对竖向承载力的影响很小;由图7(c)可知,当0≤H/Hult≤0.8时,弯矩承载力随着水平荷载的增大而增大。传统吸力基础的弯矩承载力增幅最大,最大值为1.35Mult;对裙式吸力基础,裙宽裙高的改变对弯矩承载力的影响规律不明显。当-1≤H/Hult≤0时,弯矩承载力随着水平荷载的增大而减小,此外工况2和工况3、工况4和工况5的包络线几乎重合,说明此时裙宽对吸力基础的承载力比裙高吸力基础的承载力影响更大。

图7 V-H、V-M、H-M荷载下承载力归一化破坏包络线Fig.7 V-H,V-M and H-M normalized failure envelope
为了能够进一步地研究吸力基础的承载特性,参考文献[20],并根据图7(a)、图7(b)结果得到吸力基础承载力归一化破坏包络线表达式为
(1)
(2)
式中:V、H分别为竖向、水平荷载;Vult、Hult为对应方向的极限承载力;α1、β1、α2、β2为相关拟合参数,不同工况下,拟合相关参数值如表3所示。
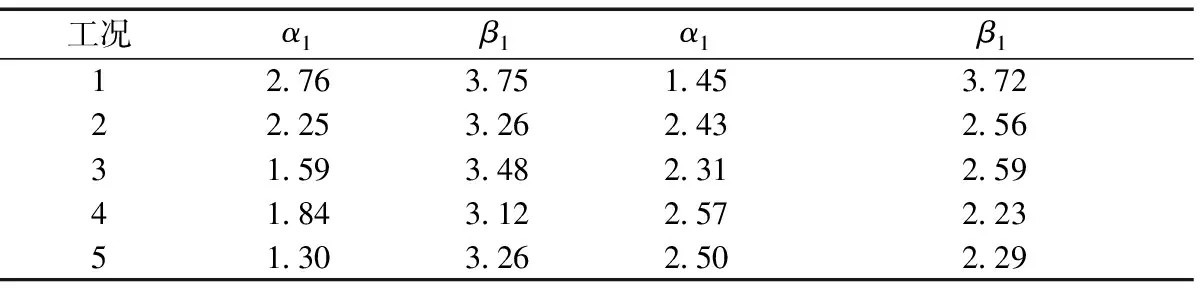
表3 α1、β1、α2、β2 取值Table 3 α1,β1,α2,β2 values
2.2 V-H-M三维复合荷载作用下的结果分
竖向荷载分别为V=0、V=0.4Vult、V=0.7Vult和V=0.9Vult时,在两种荷载复合加载(H-M)作用下不同吸力基础破坏包络线。由图8可知,随着竖向荷载的增大,H-M包络线的范围逐渐减小。
根据图8,绘制不同吸力基础在V-H-M组合荷载作用下三维破坏包络面。由图9可知,破坏包络面近似可以看作是一个1/4椭球体形状。通过对比数值模拟得出的空间破坏包络曲面和实际荷载下的吸力基础的承载特性,就可以准确了解此时地基上的吸力基础的受力状态。当实际所受荷载在曲面里面的时候,吸力基础是稳定的;当实际所受荷载在曲面外面的时候,吸力基础失稳破坏;当实际所受荷载在曲面上时,吸力基础处于极限平衡状态。

图8 H-M平面上不同竖向荷载的破坏包络线Fig.8 Failure envelopes of foundation in the H-M plane for different V

图9 V-H-M三维破坏包络面Fig.9 3D failure envelope of foundation in the V-H-M loads pace
进一步地,根据有限元模拟得出的组合荷载作用下基础失稳三维破坏包络面,参考Taiebat等[21]提出的经验公式并加以修正,提出裙式吸力基础在V-H-M荷载空间内的失稳破坏三维包络面的数学表达式为

(3)
式(3)中:M为施加的弯矩荷载;Mult为对应的弯矩极限荷载;α、β为相关拟合参数。通过验算,各工况吸力基础的拟合参数α、β取值如表4所示。
3 结论
通过数值模拟,分析得到裙式吸力基础和传统吸力基础再复合荷载作用下的承载能力特点,得到如下的结论。

表4 α和β取值Table 4 α and β values
(1)在V-H、V-M、H-M二维复合荷载作用下裙式吸力基础相比较传统吸力基础而言,其承载能力更大,不容易失稳破坏。
(2)裙结构尺寸对裙式吸力基础复合承载力有影响,裙宽、裙高越大,裙式吸力基础的复合承载力越大,裙宽对裙式吸力基础的复合承载力影响大于裙高。
(3)绘制了V-H、V-M、H-M二维复合荷载无量纲化破坏包络线和归一化破坏包络线及V-H-M三维复合荷载作用下承载力三维破坏包络面,并对其进行拟合,得到了椭圆曲线方程,可供工程实际使用。
