高中数学教师专门内容知识的调查研究

齐 春 燕

(岭南师范学院 数学与统计学院，广东 湛江 524048)

一、问题的提出

数学教师的数学教学知识自20世纪80年代起就受到数学教育工作者的重视[1-2]，国内外已有许多关于数学教师教学知识的文献，其中美国Michigan大学的Ball及其研究团队[3-4]，经过多年的探索提出了面向教学的数学知识(Mathematical Knowledge for Teaching，简称MKT)理论，该理论把数学教师的教学知识(MKT)划分为六部分，“专门内容知识(Specialized Content Knowledge，简称SCK)”是其重要的成分之一，是指从事数学教学的个体所具有的独特的知识，并通过实践研究总结了SCK可通过八个方面的能力体现出来。Bair等人[5]在该文的基础上对数学教师的SCK进行了进一步的研究，提出了数学教师SCK新的理论框架，SCK包括四部分：能够正确地解决任务，解释他们的工作，证明他们的推理并建立连接；使用多重表征的能力；识别、使用和概括概念上相似问题之间的关系的能力和问题提出的能力,并给出了SCK的五级水平划分标准。

通过学习数学史可以提高教师MKT的研究近年来也受到数学教育学者的关注[6-8]，其实，对于许多“为什么”的回答，需要教师拥有专门化的知识，而数学史就是这样的专门化知识。对于数学概念、公式和定理的形成和来源都需要通过数学史的知识来丰富教师的专门内容知识，数学教师SCK掌握的多少和水平直接影响到MKT的其他几个方面。我们将SCK中与数学史相关的部分定义为“基于数学史的专门内容知识”(History-based Specialized Content Knowledge，简称 HSCK)。比如高中三角学的内容(三角函数、三角恒等变换和解三角形)就包含着丰富的数学史内容，对于三角学的起源、单位圆的背景、任意角及弧度制引入的必要性等知识的缺乏直接影响着教师对三角学内容的理解和对学生有关知识的传播。本研究的问题是：高中数学教师拥有三角学HSCK的现状是怎样的。

二、研究设计与实施

(一)问卷的编制

最近，国内外已有很多从不同领域来测量SCK的研究[9-10], 这些研究领域涉及有代数、统计和分数乘法等，Ball团队开发了测量小学数学职前教师教学的问卷，Bair等人开发了有关代数推理和数论方面的问卷，黄友初[11]105-120在庞雅丽、苏意雯、李国强等人问卷的基础上开发了有关初中内容的问卷。但这些问卷涉及高中内容的很少，尤其通过某个确定的单元来考察教师SCK的问卷很缺乏。

本研究基于HPM 理论和 SCK 理论，确立了HSCK的六个组成成分：“回应与解释知识(KRE)”“探究与运用知识(KIA)”“表征与关联知识(KRC)”“编题与设问知识(KPP)”“评估与决策知识(KAD)”和“判断与修正知识(KJR)”，并对每个成分分别建立了四级水平的评价指标，如表1所示。

表1 HSCK六种成分水平划分表

为了保证问卷的信度和效度，首先通过7位一线的高中数学教师的预测后，请了一位数学史与数学教育专家和7位数学教育的博士进行审阅，根据修改建议修改后形成了有关“高中三角学SCK问卷调查”。

问卷由18个问题构成，其中前14题是选择题，主要考察教师的“回应与解释知识”“探究与运用知识”“评估与决策知识”和“判断与修正知识”，每题都有四个选项，教师对问题的理解不同就会选择不同的答案，每一个答案对应着不同的水平划分；后四题是主观题，主要考察教师的“表征与关联知识”和“编题与设问知识”。

(二)被试

为了考察高中数学教师HSCK的现状，本研究中在条件便利的情况下选择浙江省、江苏省、上海市和广东省市中学的高中数学教师作为调查对象，这些教师所在学校来自不同的等级，有些是本地区的重点高中，有些是普通高中，还有某师范大学攻读教育硕士、教龄为2年的58名师范生作为研究对象，这58名师范生来自全国各地的20多个省市，绝大部分毕业于数学系。本研究共收到311份问卷，有效问卷300份。按教龄、学位和接触数学史的经历对教师进行分类的情况如表2所示。

表2 300名被试的基本情况(N=300)

三、结果与分析

从不同教龄、不同学位和不同数学史经历三个不同视角分别分析教师HSCK六个成分的掌握情况。

(一)对不同教龄教师问卷的分析

300名教师按照教龄分为：0-5年、6-10年、11-15年、16-20年和21年以上五个阶段，在每一个阶段教师对三角学内容的理解和掌握的程度是不同的。研究者使用SPSS 19.0软件通过单因素方差检验分别分析六种成分的差异显著性。表3是对不同教龄教师HSCK各成分的描述统计。

表3 不同教龄教师HSCK描述统计

通过SPSS19.0对300名教师KRE、KIA、KAD和KJR总体均分的方差齐性检验结果可知：显著性概率Sig.值(即P值)为0.070，即P>0.05。这表明各教龄组的方差在0.05的显著性水平上差异不显著，即各组方差为齐性。所以选择用LSD法进行各组均值之间的多重比较，可以看出0-5年和11-15年、0-5年和16-20年教龄进行比较的P值分别为0.004和0.016，都小于0.05，这说明0-5年教龄的教师与11-15年和16-20年教龄教师KRE、KIA、KAD和KJR总体平均成绩在0.05显著性水平上差异显著。

而KRC和KPP总体均分的方差齐性检验结果是：显著性概率Sig.值(即P值)为0.422，即P>0.05。这表明各教龄组的方差在0.05的显著性水平上差异不显著。选择用LSD法进行各组均值之间的多重比较后可以看出各组教龄教师KRC和KPP总体平均成绩在0.05显著性水平上差异不显著。

(二)对不同学位教师问卷总的分析

300名教师中有学士学位和硕士学位两种，硕士学位是指获得了教育硕士的教师。研究者使用SPSS 19.0软件通过单因素方差检验分别分析六种成分的差异显著性。表4是不同学位教师HSCK成分现状的SPSS19.0分析的结果。

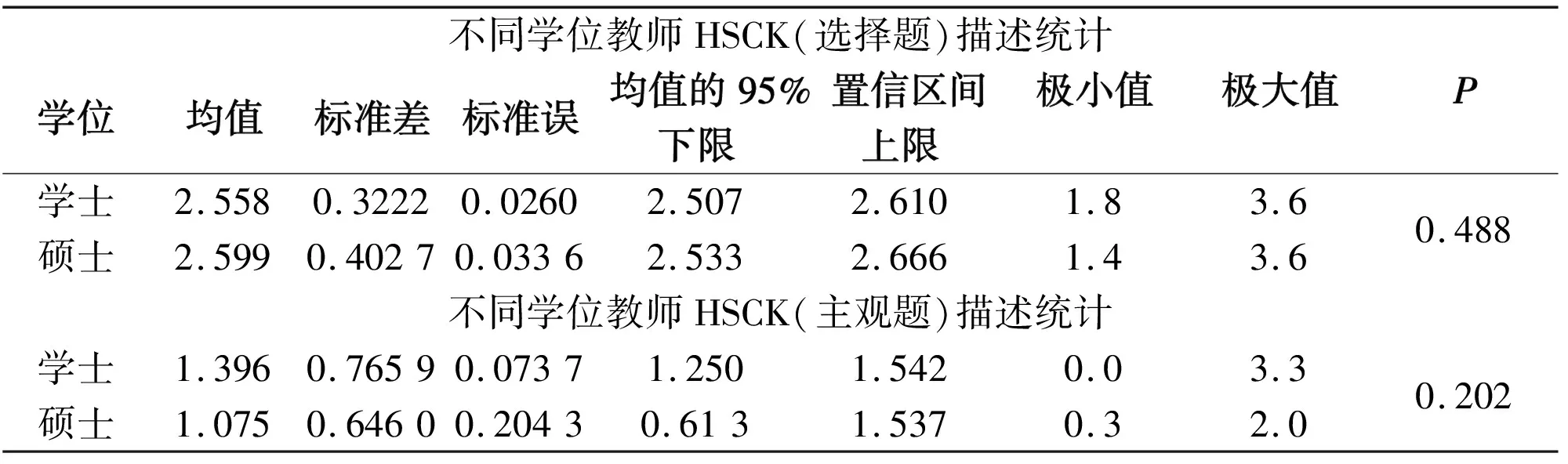
表4 不同学位教师HSCK描述统计

通过SPSS19.0对300名教师KRE、KIA、KAD和KJR总体均分的方差齐性检验结果可知：具有学士学位教师HSCK总体均值为2.228，具有硕士学位教师HSCK总体均值为2.599，进行比较的P值为0.488大于0.05，这说明具有学士学位和硕士学位教师HSCK的总体平均成绩在0.05显著性水平上差异不显著。

而KRC和KPP总体均分的方差齐性检验结果是P值为0.202大于0.05，这说明具有学士学位和硕士学位教师HSCK的总体平均成绩在0.05显著性水平上差异不显著。

(三)对不同数学史经历教师问卷总的分析

研究者把接触数学史的经历分成了四个部分，本节是对不同数学史经历教师HSCK掌握的现状进行的分析。表5是不同数学史经历教师关于HSCK成分现状的SPSS19.0分析的结果。

表5 不同数学史经历教师HSCK描述统计

通过SPSS 19.0对300名教师KRE，KIA，KAD和KJR总体均分的方差齐性检验结果可知：显著性概率Sig.值(即P值)为0.176，即P>0.05.这表明各教龄组的方差在0.05的显著性水平上差异不显著，即各组方差为齐性。所以选择用LSD法进行各组均值之间的多重比较，从表10中可以看出数学史经历不同的四组教师HSCK的总体平均成绩在0.05显著性水平上差异不显著。

通过SPSS 19.0对300名教师KRC和KPP总体均分的方差齐性检验结果可知：显著性概率Sig.值(即P值)为0.376，即P>0.05.这表明各数学史不同经历组的方差在0.05的显著性水平上差异不显著，即各组方差为齐性。所以选择用LSD法进行各组均值之间的多重比较，从表5中可以看出数学史经历不同的四组教师HSCK的总体平均成绩在0.05显著性水平上差异不显著，但数学史经历丰富的教师在“表征与关联知识”和“编题与设问知识”的表现上要比其他数学史经历阶段的教师要好。

四、结论与启示

通过以上分析可得到高中数学教师拥有三角学HSCK的现状是：

其一，不同教龄的高中数学教师对于HSCK中“回应与解释知识”“探究与运用知识”“评价与决策知识”“表征与关联知识”和“编题与设问知识”的表现水平上没有显著性差异。因教学经验丰富的教师已形成了自己的教学风格，对教材的处理已有自己的各种策略，所以在“判断与修正知识”方面反而是新手教师表现得更好，原因是新手教师大部分学习过有关数学史的课程，对三角学的历史发展脉络较清楚，所以在“判断与修正知识”的表现上比其他教龄段的教师要好；

其二，具有学士和硕士学位的教师，HSCK的水平无显著性差异；

其三，数学史经历丰富的教师在“表征与关联知识”和“编题与设问知识”的表现上要比其他数学史经历阶段的教师要好；

其四，HSCK的六个成分之间存在着紧密的、相互制约、相互促进的关系。

从以上结论中可得到以下启示：

首先，在教师教育培训中可以增加数学史料的学习，通过了解学科的历史发展过程能提升教师的专业素质；

其次，在教材编写中可以适当增加概念、命题的历史发展过程，通过学习概念、命题的来龙去脉提高教师对数学本质的理解；

最后，根据课程标准的要求，加大在高考中对数学文化的考核，加强教师对数学史料的更深理解，把数学文化融入课堂当成常态课进行教学。