受春秋战国史实启发的帝国竞争改进算法

王贵林，李 斌

（福建工程学院交通运输学院，福州 350118）

（*通信作者电子邮箱whutmse2007_lb@126.com）

0 引言

Gargari 等［1］于2007 年提出了帝国竞争算法（Imperialist Competitive Algorithm，ICA），其灵感源于人类社会帝国殖民竞争机制，是一种完全受社会行为启发的群体随机优化搜索算法。该算法自提出后，已在不同领域得到广泛研究应用。例如，Bernal 等［2］探讨了ICA 在数学函数优化中的应用；陈孟辉等［3］、Liu 等［4］、张清勇等［5］分别运用ICA 求解旅行商问题、非线性约束优化问题和异构工厂分布式并行机调度问题；Fan等［6］、Khalilnejad 等［7］、颜波等［8］基于ICA，分别对起重机金属结构、风力/光伏混合电解槽和多产品供应链设计过程进行了优化；Hasanzade-Inallu 等［9］、刘敬浩等［10］将ICA 与神经网络结合，分别用于预测混凝土梁的抗剪强度、构造入侵检测模型；Illias等［11］、李明等［12］使用ICA估算微变压器参数、实现高维多目标柔性作业车间调度。原始ICA 局部搜索能力较强，收敛快，但由于群体多样性在迭代过程中降低过快、帝国之间缺乏有效的信息交互等问题，容易“早收早敛”，特别是在优化高维多模问题时，易陷入局部最优。

针对上述问题，国内外已有许多学者对ICA 的性能改进以及实际应用进行了大量的研究，也取得了一定的进展。例如，算法的提出者Gargari［13］给出了改进算法的Mathlab 源代码，调整了殖民地的权值，增加了殖民地革命和帝国合并机制；郭秀萍等［14］引入变邻域搜索，增加了种群多样性，改善了解的质量并提高了算法效率；Bahrami等［15］利用混沌映射来调整殖民地向帝国位置的运动角度；Lin等［16］用人工产生国家取代较弱的帝国主义国家，以此来增强帝国之间的信息交互；Ardeh 等［17］通过引入探索者和保留策略的概念，采用动态种群机制对原算法进行了改进；Xu 等［18］引入高斯变异、柯西变异和莱维变异等变异算子来改变帝国主义者行为；郭婉青等［19］采用微分进化算子和克隆进化算子增强殖民地之间、帝国之间的信息交互。这些改进方案主要采用调整算法流程、引入随机因素、融合其他算法等方式实现，虽然在不同程度上提升了算法的寻优性能和稳定性，但普遍缺乏对核心运行机制的研究改进，难以从根本上解决ICA 存在的问题；没有加入判断并跳出局部最优的方案，限制了算法对高维多模函数的适用性；同时，个别复杂因子的引入也在一定程度上降低了算法的运行效率。

本文借鉴中国历史上春秋战国时期诸侯国竞争称霸的行为对ICA 进行改进，命名为受春秋战国史实启发的帝国竞争改进算法（Improved ICA Inspired by Spring and Autumn Period，SAICA），探索解决原始ICA 受初始国家影响大、帝国间缺乏有效信息交互、容易早收早敛等问题。通过在标准函数和CEC2017 测试函数上进行实验对比，验证了改进算法的全局搜索、稳定性及跳出局部最优能力。经Kendall相关性分析显示，改进算法与原始算法具有显著差异性，且同化过程的改进措施发挥了关键的作用。

1 帝国竞争算法

ICA 的基本流程如图1 所示，可归纳为国家初始化、殖民地同化、帝国竞争、国家汇聚四个流程。

1.1 国家初始化

定义初始国家为：

与遗传算法每一个向量代表一个染色体不同的是，数列中的每一维代表国家的一个特征。

国家的势力值由所求的函数值来表示，即：

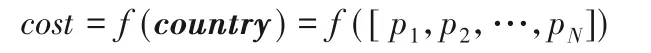
算法开始时，随机产生Npop个初始国家，并根据势力大小划分为两种类型：势力最大的前Nimp个国家为宗主国，其余的为殖民地国家，按照下列流程，根据宗主国的势力来划分殖民地的归属国。

1）根据各个帝国对应的函数值cn，计算帝国主义国家的归一化势力值Cn：

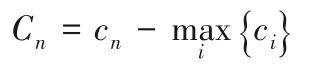
2）计算归一化势力的相对值Pn，以此得出每个帝国占有殖民地的初始数量NCn：

其中：Ncol表示殖民地国家的数目；round{}为四舍五入取整函数。

3）将所有殖民地国家随机分配到各宗主国，组成初始的Nimp个帝国。

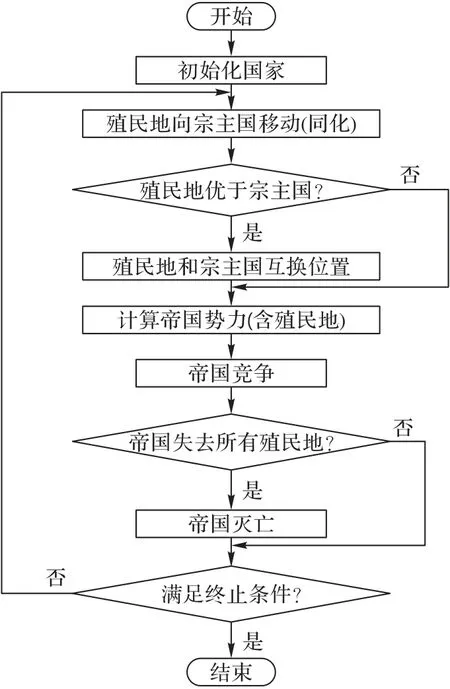
图1 帝国竞争算法流程Fig.1 Fowchart of ICA

1.2 殖民地同化

宗主国为了便于管辖其拥有的殖民地国家，需要在政治、经济、文化等各方面进行殖民同化，算法通过殖民地向宗主国移动来表示，其移动过程如图2所示。

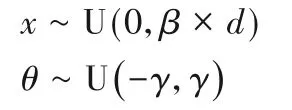
其中：x表示移动距离；d表示殖民地和宗主国间的距离；β为移动参数，取值大于1 使殖民地国家能从前后方向朝宗主国靠近；为了扩大搜索范围，加入一个随机的角度偏移参数θ，其中γ值一般为π4。

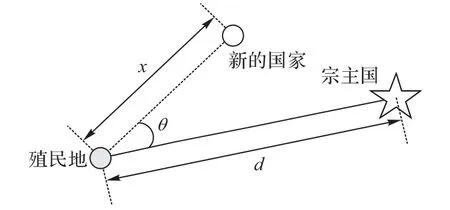
图2 殖民地移动过程Fig.2 Colony moving process

在同化过程中，如果移动后某个殖民地势力大于其宗主国，则殖民地和宗主国互换位置，帝国中的其他殖民地向新宗主国的位置移动。这个过程确保了宗主国的位置在寻优过程中始终保持相对最优。

1.3 帝国竞争

所有宗主国都想要占领其他宗主国的殖民地以增强帝国的势力，这种竞争机制使强大的帝国更加强大，弱小的帝国将逐渐衰落，直至消亡。原始ICA 选取最弱帝国中的最弱殖民地作为帝国竞争的对象，所有帝国都有机会占有这个殖民地国家，且帝国势力越大，占有的概率越大。

帝国势力值TCn的计算方法如下：

其中：Cost(imperialistn) 为宗主国的归一化势力值；Cost(colonies)为帝国所辖殖民地的归一化势力值；mean{}为均值函数；ξ表示殖民地占帝国势力的权重值。可以看出，帝国总势力值为宗主国及其所辖殖民地的势力值之和。

1.4 国家汇聚

竞争过程中，势力较弱的帝国因失去殖民地而越发弱小，直至所有殖民地被其他帝国所占有，则该帝国灭亡。

经过多次迭代，帝国相继灭亡，在理想状态下，最后仅留存唯一一个统辖所有殖民地的国家。此时，所有国家都汇聚于一点，宗主国和殖民地的势力值完全相同，算法结束。

2 受春秋战国史实启发的帝国竞争改进算法

2.1 春秋战国历史背景

春秋战国时期（公元前770 年—公元前221 年）又称东周时期。周朝初期，周王朝把宗室和功臣分封到各个战略要地或王室周围，以达到屏藩王室和开疆拓土的职责，从而形成了上千之多的诸侯国。春秋初期，平王东迁洛阳，周室开始衰微，中原各国也因社会经济条件不同，国家间争夺霸主的局面逐渐显现。大国依靠强大的政治军事力量，不断侵吞兼并小国，强化势力范围；小国也通过变革、合并等方式以期获得一定的生存空间。经过二三百年，至春秋后期，仅剩下几十个较大的诸侯国。到战国时期，形成七雄争霸的格局，直至秦灭六国，统一天下。

在这段历史时期，一种奇特的外交策略应运而生——“合纵连横”。即在国家斗争过程中，较弱的国家为了生存，互相联合借以抵抗强大国家的侵袭。抵抗一经失败，又纷纷投靠强国以图自保，形成了“合众弱以攻一强”的“合纵”策略及“事一强以攻众弱”的“连横”策略。

2.2 改进的帝国竞争算法

ICA 模拟帝国竞争机制，通过非最优解向较优解靠近、较优解的位置更新、竞争汇聚等实现寻优能力。SAICA 在保留ICA核心思想基础上，提出了三种改进措施，具体步骤如下：

1）初始化设置，包括初始国家数量Npop、帝国数量Nimp、殖民地数量Ncol、移动参数值β、迭代次数。

2）随机产生初始国家，按照归一化势力值区分强国和弱国，强国直接保留，弱国联合产生新的国家。新国家势力值的大小将决定其取代已有强国或被淘汰，最后留存的国家进入帝国竞争。

3）由势力最强的Nimp个国家担任宗主国分别组成帝国，并占有相应比例的殖民地。帝国内部的每个殖民地各特征向量分别向宗主国对应的特征向量移动靠近，移动过程中如果殖民地势力值大于宗主国，则取而代之，其他殖民地向新的宗主国移动。

4）计算帝国总归一化势力值，最弱帝国的最弱殖民地将被其他帝国占有，占有概率与帝国势力成正比。殖民地为零的帝国将淘汰灭亡。

5）连续出现相同最优值则判断是否陷入局部最优，根据设定的跳出方案摆脱困境。

6）反复迭代，直至达到设定的最大迭代次数。

改进算法的流程如图3所示。

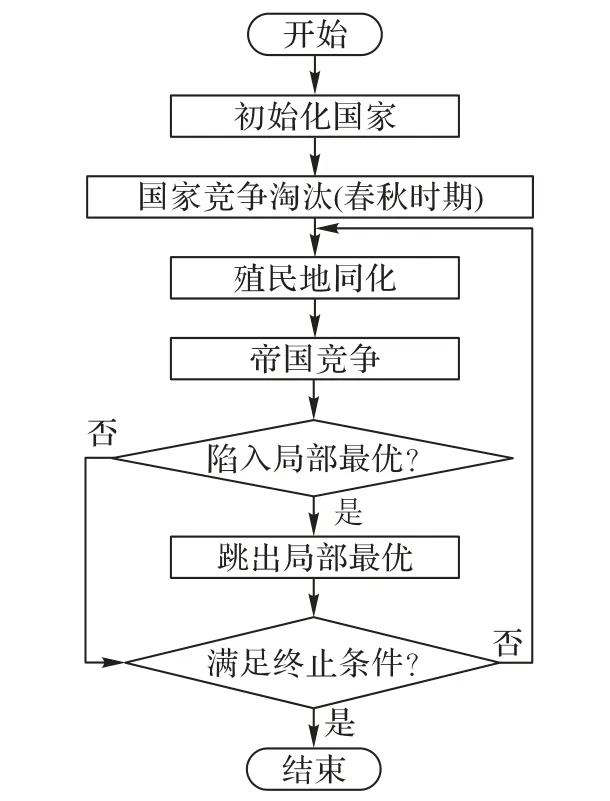
图3 SAICA流程Fig.3 Flowchart of SAICA

2.2.1 改善初始国家产生机制

根据ICA 的原理分析，初始国家随机产生导致难以保证种群的优质性和稳定性。本文借鉴春秋战国时期诸侯国竞争淘汰的历史情况，尝试一种新的初始国家产生机制，具体流程如图4所示。

图4 初始化国家流程Fig.4 Flowchart of country initialization

算法开始时，随机产生较大数量的国家，一般为ICA 国家数量的2～4倍，这样既能通过竞争筛选保留质量较好的国家，又不会对算法的复杂度及运行效率产生较大影响。其中，一部分势力较强的国家留用，其余相对弱小国家为避免淘汰，联合其他国家增强势力以图自保。具体步骤如下：

1）按照一定数量随机选择联合的国家。

2）计算各国家的势力大小，获得权值。

3）依据权值取各个国家的位置信息组建合并成新的国家，如果新国家势力值超过留用国家，则取而代之，否则淘汰出局。

上述竞争筛选过程增强了国家间的信息交流，保留了优良的位置信息，形成了较好的算法初始种群。

2.2.2 改进帝国同化方式

ICA 帝国同化过程通过殖民地向宗主国整体移动实现，移动参数β值取2.0 确保殖民地从前后两个方向向宗主国靠近。在现实世界中，殖民同化一般伴随政治、经济、文化等各层面渗透转变。借鉴这一思想，将殖民地国家移动过程变更为各特征分量向宗主国对应的特征分量移动过程，如图5所示。

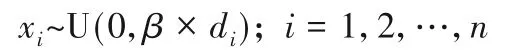
各特征分量单独移动，若移动参数值为β，则其最大的移动距离为：

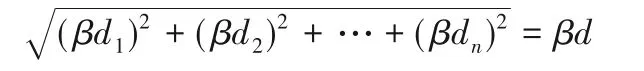
其中，di(i=1，2，…，n)为殖民地各特征分量与帝国对应特征分量间的距离。为确保从正反两面向目标靠近，β取值应大于1.0。经反复测实验证：当β取值由1.0 逐步增大时，求解精度逐渐提升；不同的测试函数在β值取1.5～1.8 时，能够获得最佳的寻优精度；β取1.8 之后，求解精度又随β值增大而逐渐降低。因此，针对不同的目标函数，将移动参数β值限定在1.5～1.8 区间能获得较好的效果。在实验或实际应用中，可先进行简单的代入测试，明确参数值。

图5 特征分量单独移动Fig.5 Feature components moving separately

为便于比较改进算法与原算法移动机制的区别，图6 展示了二维平面上两种算法的搜索范围差异。ICA 的搜索范围是以2d为半径的扇形，改进算法则是以各个分量的最大移动范围为边构成的矩形。一方面，各特征分量单独移动增强了灵活性和随机性，开发能力更强；另一方面，矩形搜索范围相对较小，改善了多个目标靠近时搜索区域的重叠与覆盖问题（见图7），效率更高。

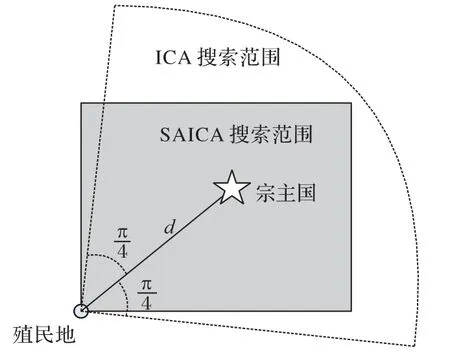
图6 搜索范围对比Fig.6 Search scope comparison

2.2.3 增加跳出局部最优的策略

针对原ICA 的“早熟”问题，提出了一种跳出局部最优的策略：如果连续多次出现相同的最优值，则判定陷入局部最优，此时，宗主国按照选定的方案跳出局部最优。

跳出局部最优的方案有多种，本文给出了三种方案并进行测试：一是取各宗主国的算术平均值作为新的移动目标点，本文记为SAICA-Ⅰ；二是按照各个宗主国的势力取加权平均值作为新的移动目标点，本文记为SAICA-Ⅱ；三是宗主国自身一定比例的位置信息随机发生改变，本文将这一比例设定为10%，记为SAICA-Ⅲ。前两种方案构建的新移动目标点都包含了其他宗主国的信息，增强了信息交互；第三种方案通过随机变化跳出局部最优，提高了种群多样性。

图7 搜索区域交叉和覆盖Fig.7 Search area crossing and covering

2.3 改进算法的开发、勘探能力及二者的平衡性分析

ICA 在平衡开发和勘探能力方面有所不足，缺乏有效的信息交互，帝国的合并、覆灭使种群多样性快速降低，高维函数适用性不强。针对上述问题，SAICA 在初始化国家阶段利用竞争淘汰机制增强信息交互，保留优势种群；在多次迭代后种群多样性大幅降低阶段增加跳出局部最优的机制，为种群多样性的恢复提供了一条路径，二者前后呼应配合。同时，同化机制的改进，增强了搜索的灵活性和效率，在不影响勘探能力的前提下，提升了开发能力。因此，总体来看，改进算法相较ICA，开发和勘探能力同时得到增强，且勘探能力提升的措施相对更多，二者的平衡性更趋于合理。

3 基准测试函数实验对比

3.1 改进有效性验证

为了测试SAICA 的性能，本文首先选取8 个经典标准函数进行实验，如表1 所示，其中前两个为单模函数，其余为多模函数。

表1 标准测试函数Tab.1 Benchmark test functions

该实验对SAICA-Ⅰ、SAICA-Ⅱ、SAICA-Ⅲ与遗传算法（Genetic Algorithm，GA）、粒子群优化（Particle Swarm Optimization，PSO）算法、原始ICA 进行对比分析。各种算法在相同的硬件条件下分别独立运行50 次，每次运行最大迭代次数Max_Iter为1 000，统计计算各算法运行结果的最小值、均值及标准差，测试函数的维度分别取30、50 和100，实验结果如表2～4所示，其中最优结果用粗体标出。由分析可知，在30 维条件下，SAICA 对所有测试函数的寻优能力优于GA、PSO 和ICA；随着维数的增加，各算法的寻优精度均有所下降，但改进算法仍保持一定的精度优势。

各算法在测试函数上的收敛曲线如图8 所示，可以看出，SAICA 的曲线陡峭，且陡峭曲线到相对水平的转折点出现得比较早，说明算法收敛快，与ICA 差别不大，相较GA和PSO算法有较大优势。测试的8 个标准函数均能在500 次迭代内收敛至相对优值，其中5 个能够在100 次迭代内完成。例如Sphere、Rastrigin函数，SAICA用50次迭代就能达到GA和PSO算法1 000次迭代得到的最优解。另外，SAICA 的收敛曲线呈现或多或少的起伏波动，其中Rastrigin、Michalewicz、Schwefel函数尤为明显，这是陷入局部最优后，跳出机制发挥了作用。

从SAICA 三种跳出局部最优的方案对比分析可以看出，三者实验结果差别不大，特别是单模函数CF1、CF2 由于不存在局部最优，跳出机制不影响搜寻精度。对多模函数CF3～CF6，SAICA-Ⅲ相较前两种方案，随机因素的引入有利于提升种群多样性，勘探能力更强一些，特别在求解高维函数时，可通过迭代次数的增加，提高其寻优精度。因此，后续的实验均采用第三种方案。

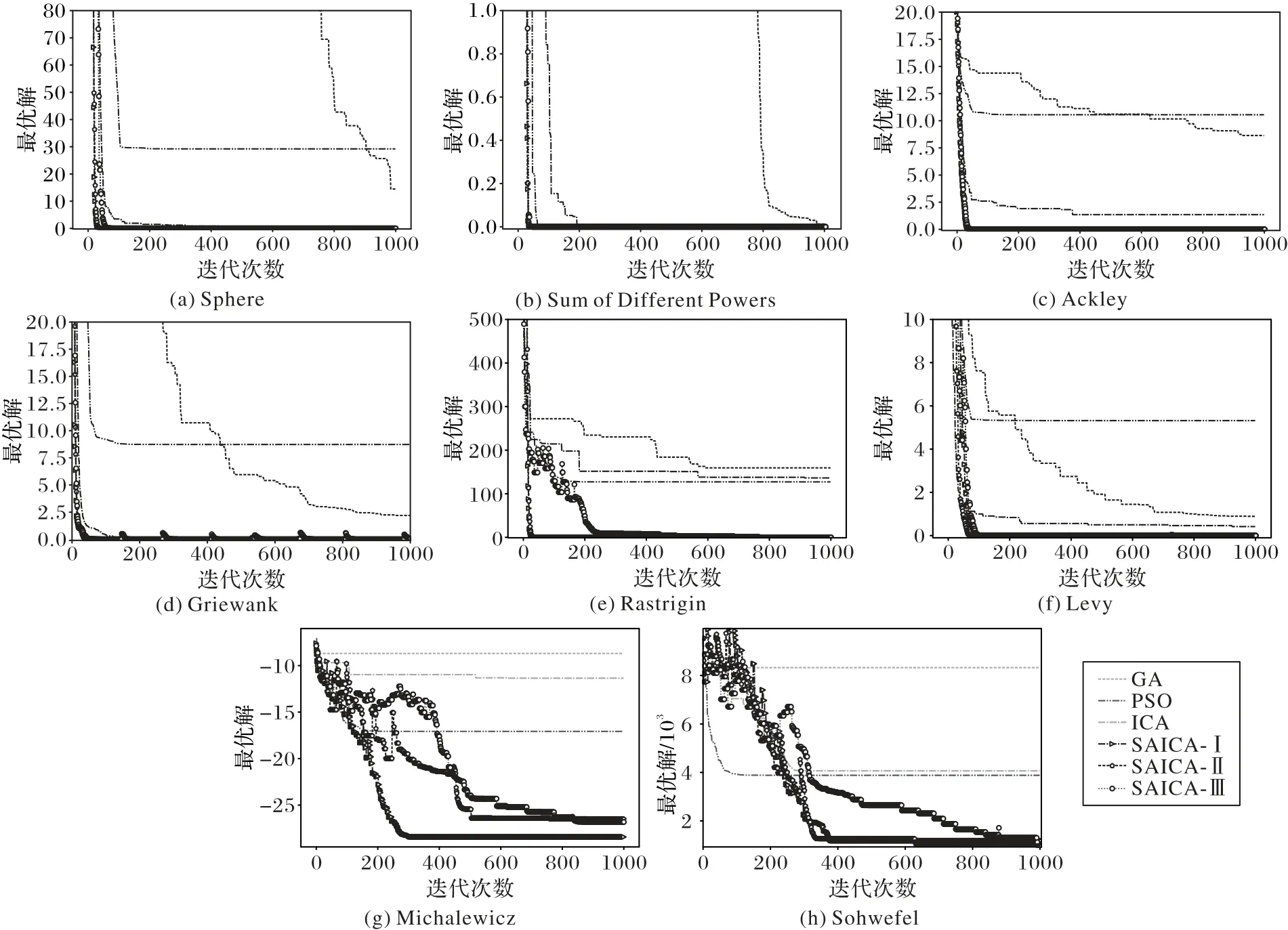
图8 算法收敛曲线Fig.8 Algorithm convergence curves

3.2 改进性能测试

为了验证改进算法的寻优性能和稳定性，选择CEC2017中的6 个测试函数（表5），与5 个具有代表性的先进算法对比分析，分别为：策略自适应差分进化（Differential Evolution algorithm with Strategy adaptation，SaDE）算法、球形搜索进化（Spherical Evolution，SE）算法、郊狼优化算法（Coyote Optimization Algorithm，COA）与 灰 狼 优 化（Grey Wolf Optimizer，GWO）算法的混合算法（Hybrid COA with GWO，HCOAG）、基于精英学习策略的动态多群粒子群优化（Dynamic Multi-Swarm Particle Swarm Optimization based on an Elite Learning Strategy，DMS-PSO-EL）算法以及基于多精英采样和差分搜索的分布估计算法（Estimation Distribution Algorithm based on Multiple elites sampling and individuals Differential Search，EDA-M/D）。其中，SaDE 引入了自适应学习机制，根据进化的不同阶段匹配向量生成策略及其控制参数；SE 在传统的超立方体搜索基础上衍生出一种球形搜索模式，并引入了进化算法；HCOAG 采用正弦交叉策略，将COA和GWO 的两种改进算法融合运用；DMS-PSO-EL 把进化过程划分为前后两个阶段，采用动态多群和学习策略实现勘探和开发能力的提升；EDA-M/D 借助多精英采样与差分搜索的自适应协同提升算法的寻优性能和稳定性。这些对比算法既包含经典的进化算法、粒子群算法的改进型，又包含郊狼算法、分布估计等新型算法的优化，涵盖了策略调整、自适应学习、算法混合等常用的改进方案，且在仿真测试中都取得了较好的实验结果，具有较高的代表性。

表5 中f1 为单峰函数，f4、f9 为简单多峰函数，f12、f16 为混合函数，f29 为复合函数，所有函数均经过偏移翻转。运行迭代次数设置为1 000，每个测试函数至少运行50 次，取运行结果与最优解差值的算术平均值和均方差进行比较。其中，测试结果的算术平均值可以比较算法的寻优能力，标准差可以比较算法的稳定性。实验结果如表6 所示，所有算法计算结果的最优值以粗体显示。其中SaDE、SE 的实验数据来自文献［20］，HCOAG 的实验数据来自文献［21］，DMS-PSO-EL的实验数据来自文献［22］、EDA-M/D 的实验数据来自文献［23］，符号#表示文献作者未提供。

分析可知，SAICA 对所有测试函数的求解均值和标准差都优于对比算法，其中，f1、f9 函数搜寻到最优解，显示本文算法有更好的寻优精度和稳定性。

表2 SAICA与GA、PSO、ICA性能对比（Max_Iter=1000，D=30）Tab.2 Performance comparison of SAICA and GA，PSO，ICA（Max_Iter=1000，D=30）

表3 SAICA与GA、PSO、ICA性能对比（Max_Iter=1000，D=50）Tab.3 Performance comparison of SAICA and GA，PSO，ICA（Max_Iter=1000，D=50）

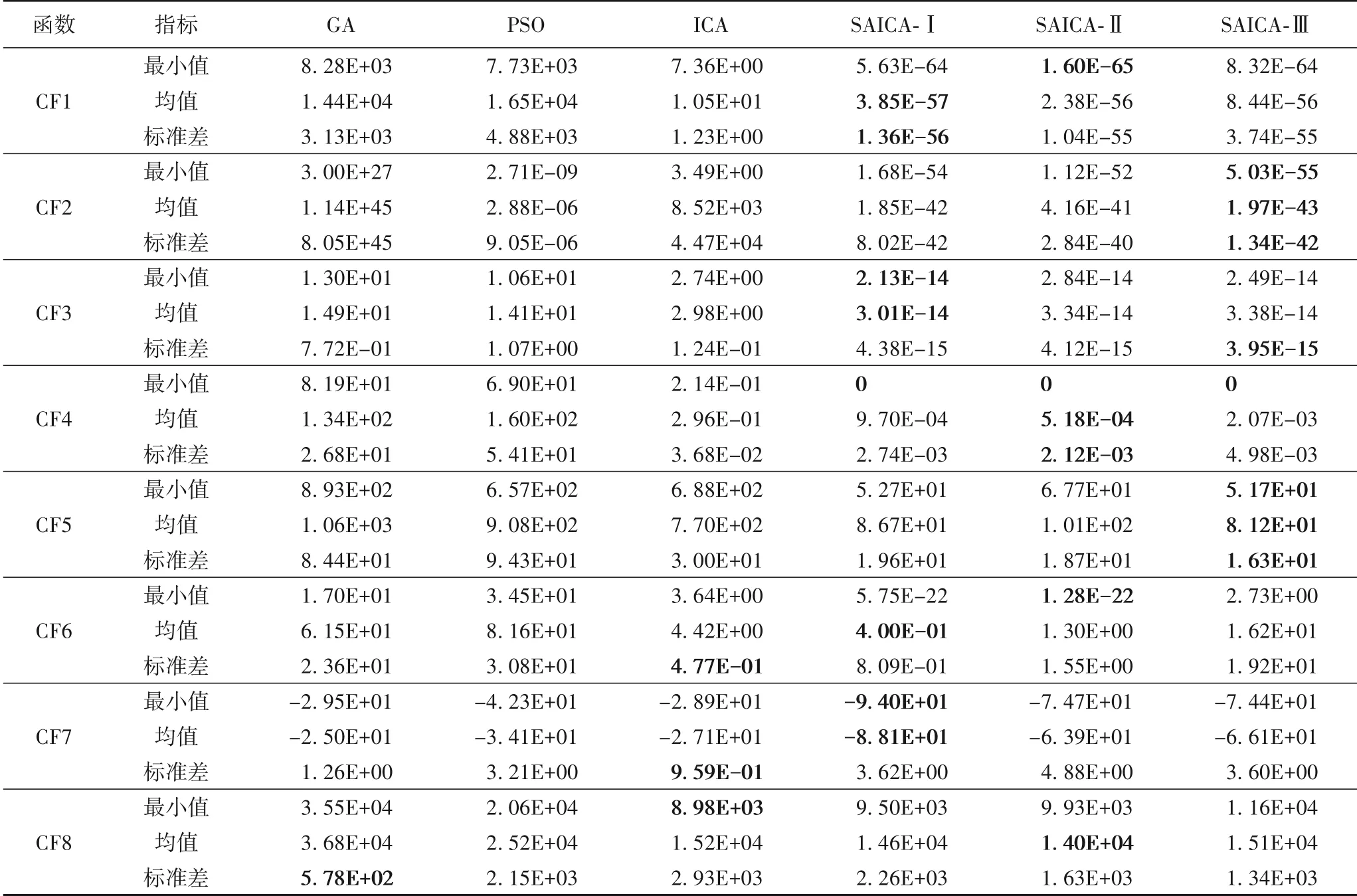
表4 SAICA与GA、PSO、ICA性能对比（Max_Iter=1000，D=100）Tab.4 Performance comparison of SAICA and GA，PSO，ICA（Max_Iter=1000，D=100）

表5 CEC2017测试函数Tab.5 CEC2017 test functions

表6 SAICA与其他先进算法性能对比（D=30）Tab.6 Performance comparison between SAICA and other advanced algorithms（D=30）

3.3 相关性检验

为了判断SAICA 与ICA 在寻优性能上是否存在显著性差异及各种改进措施的贡献度，采用Kendall相关系数法对算法的计算结果进行显著性检验。选取16 个经典测试函数，分别用ICA、SAICA 及SAICA 的三种改进措施（依次表示为SAICAA、SAICA-B、SAICA-C）进行实验，30次实验结果的均值如表7所示。

用IBM SPSS Statistics 22.0 版本对以上数据进行Kendall相关分析，结果如表8 所示。分析可知：SAICA 和ICA 之间的相关系数值为0.100，接近于0，且显著性p值为0.589＞0.05，表明SAICA 和ICA 之间没有相关关系，即SAICA 和ICA 在求解性能上存在显著差异性。SAICA 和SAICA-B 之间的相关系数值为0.783，且呈现接近于0 的显著性，表明SAICA 和SAICA-B 之间有着显著的正相关关系，即第二种改进措施发挥的作用最大。SAICA 和SAICA-A、SAICA-C 之间的相关系数值分别为0.017、0.126，从分析结果上看没有相关性，但实验数据显示SAICA 的求解精度高于仅加入一种改进措施的SAICA-B，表明另外两种改进措施能发挥一定的辅助作用。

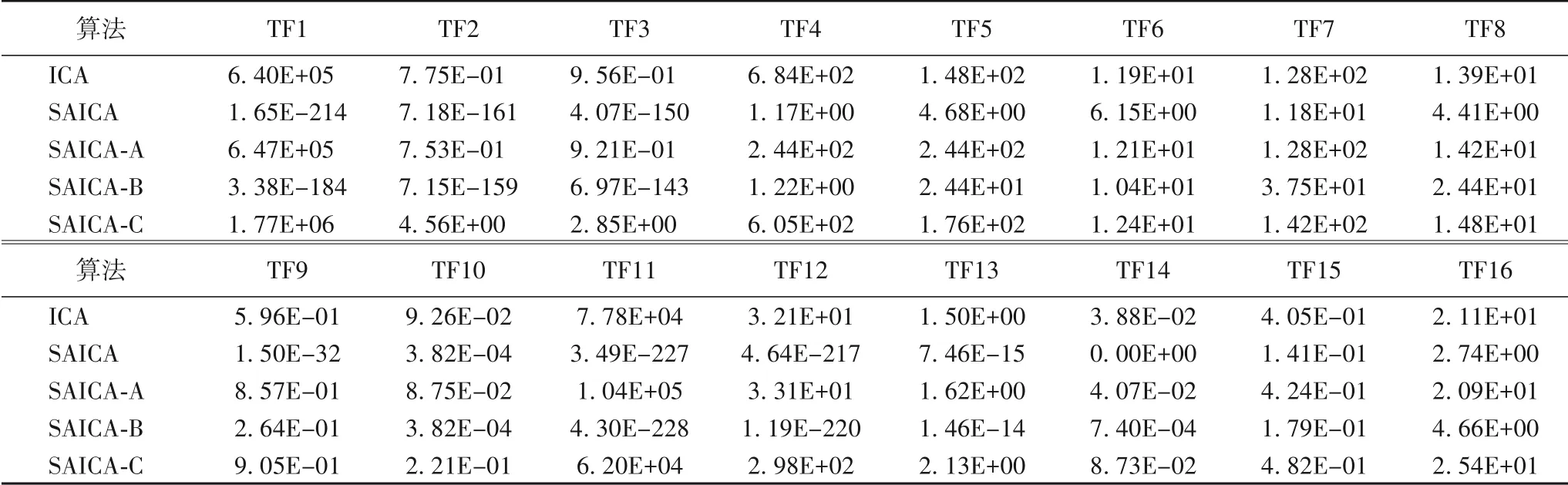
表7 ICA、SAICA及SAICA三种改进措施的实验结果Tab.7 Experimental results of ICA，SAICA and three improvement measures of SAICA

表8 Kendall相关分析结果Tab.8 Kendall correlation analysis result

4 结语

本文在ICA 框架上，基于春秋战国史实，引入“合纵连横”初始化策略、分量移动同化机制、自更新跳出局部最优方案，对原算法进行改进优化。8 个国际通用标准函数和CEC2017测试函数实验比较结果表明，本文提出的SAICA 在提高求解精度和求解效率上具备一定优势，且方法简单、复杂度低，对解决现实寻优问题有实际意义。经Kendall 相关系数分析可知，改进算法与原算法具有显著差异性。同时，在实验过程中也发现，SAICA 存在对个别高维函数寻优准确度提升不高、跳出局部最优后仍然无法寻得全局最优解等问题。下一步，将在本文研究基础上，进一步优化算法，寻求改进跳出局部最优的策略，提升对高维函数的寻优性能和覆盖面，并在解决实际问题中加以研究应用。