基于Multisim的抽样定理验证电路设计

袁宗文 唐静

摘要：抽样定理是信息传输技术的重要定理，通常验证该定理的硬件电路固化，缺少分析和设计过程，不利于理解定理的本质内容。基于Multisim仿真平台进行抽样定理的验证电路设计，首先基于信息传输理论进行系统设计，其次对设计出的系统进行仿真，最后对仿真结果进行分析，并结合仿真结果修改系统参数后再次仿真。结果表明这种做法不仅有利于全面理解抽样定理所涉及的相关理论，而且还锻炼了系统分析和设计的能力。

关键词：抽样定理;频谱;电路设计;仿真

中图分类号：TP391.9    文献标识码：A

文章编号：1009-3044（2021）36-0175-04

开放科学（资源服务）标识码（OSID）：

Circuit Design for Verification of Sampling Theorem Based on Multisim

YUAN Zong-wen， TANG Jing

（School of Electronic Engineering， Chaohu University， Hefei 238024， China）

Abstract： Sampling theorem is an important law of information transmission technology. Usually， the hardware circuit to verify the theorem is solidified. The lack of analysis and design process is not conducive to understanding the essence of the theorem. Based on the Multisim simulation platform to design the verification circuit of the sampling theorem， firstly design the system based on the information transmission theory， secondly simulate the designed system， finally analyze the simulation results， and modify the system parameters based on the simulation results and then simulate again. The results show that this approach is not only conducive to a comprehensive understanding of the relevant theories involved in the sampling theorem， but also exercises the ability of system analysis and design.

Key words： sampling theorem; spectrum; circuit design; simulation

1 引言

信號与系统课程是大学电气信息类重要的专业基础课，该课程数学要求较高，理论复杂抽象，为掌握好课程理论知识，必须辅以必要数量的实验项目。信号与系统实验通常通过实验箱完成，然而实验箱的固定化电路结构限制了学生动手能力和创新思维的培养，而且实验箱电路因为各种原因容易损坏，维修也不方便，因此软件仿真是极好的补充。Multisim软件具有强大的电路仿真能力，且易学易用，为当今高校电路教学和学习普遍使用的仿真平台[1-2]。

抽样定理是信号与系统课程重要的定理，其推导和结论都比较抽象难懂，本文在Multisim平台通过选择合适的元器件搭建出抽样定理的验证电路[3]，为便于对比分析，搭建的电路尽量与实验箱实际电路一致，仿真过程表明，该虚拟电路完全可替代实际电路，让学生掌握抽样定理的本质。

2 抽样定理理论分析

2.1 信号的频谱

傅里叶分析是分析信号的基本工具，它从另一个视角——频域来观察和理解信号，获得信号更为本质的一些特征[4]。傅里叶分析包括傅里叶级数和傅里叶变换，周期信号[f（t）]的傅里叶级数如式（1）。

[f（t）=A0+n=1∞Ancos（nω0t+?n）]                （1）

其中[A0]为直流分量，[An]为第n次谐波的振幅，也称之为振幅谱，[ω0]为基波的角频率，[T0=2π/ω0]为基波周期，[nω0]为第n次谐波的角频率，[?n]为第n次谐波的初相位，也称之为相位谱。设[Cn=1T00T0f（t）e-jnω0tdt]，则式（1）中的[An=2Cn]，[?n=?Cn]，根据这些关系可以求出周期信号展开成傅里叶级数的具体形式。本实验将对方波和三角进行抽样，它们的波形及傅里叶级数展开如下：

方波的时域波形如图1所示，其傅里叶级数展开如式（2）所示，其振幅谱如图2所示。

[fsqua（t）=4Aπcosω0t-13cos3ω0t+15cos5ω0t-17cos7ω0t+…]   （2）

三角波的时域波形如图3所示，其傅里叶级数展开如式（3）所示，其振幅谱如图4所示。

[ftria（t）=8Aπ2cosω0t+19cos3ω0t+125cos5ω0t+149cos7ω0t+…]      （3）

2.2 时域抽样定理

若带限信号[f（t）]的最高频率为[ωm]，当抽样频率[ωs≥2ωm]时，则信号[f（t）]可以用其样本值唯一地表示。

信号的抽样过程可用图5简单地描述，其中[δT（t）]为周期性冲激串，其周期[T=2π/ωs]， [fs（t）=f（t）·δT（t）]，称之为抽样信号。

如果让抽样信号[fs（t）]通过一截频[ωc]满足[ωm≤ωc<ωs-ωm]的理想低通滤波器[H（jω）]，如图6所示，则滤波器的输出就是原信号[f（t）]。

3 抽样定理验证电路设计

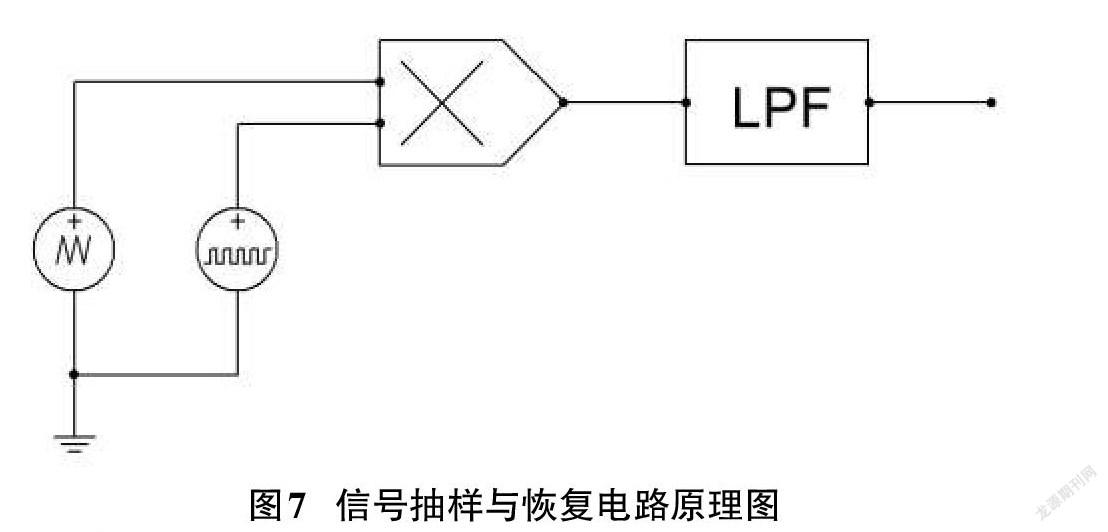
根据抽样定理，信号的抽样与恢复电路原理图可以如图7所示，其中乘法器用模拟开关代替，信号源分别是周期电压信号和脉冲电压信号，滤波器为有源低通滤波器[5-6]。

①信号源

周期信号分别选择方波信号与三角波信号，频率皆为1 KHz，振幅皆为1 V;脉冲信号的占空比为50%，幅度为5 V，其频率即为抽样频率。

②乘法器

为实现本实验的乘法功能，可以用模拟开关代替，这里选用开关速度高、宽电压范围、低噪声、低成本的4路模拟开关MC74HC4066D。

③低通滤波器

为简单、调节方便、易实现起见，选择二阶有源低通滤波器，其实现电路如图8所示。

当[R1=R2=R]、[C1=2C2=C]时，则滤波器截止频率[ωc=1.414RC]或[fc=0.225RC]。实际电路中为保证[R1=R2]，这里的[R1]、[R2]由双联调电位器取代。

3.1 方波的抽样与恢复

根据上述要求，设计出的方波信号抽样与恢复电路如 9所示，其中，V1为被抽样的方波信号，V2为周期性脉冲信号，U1A的输出为恢复信号，为降低抽样电路对滤波电路的影响，在此之间插入跟随器U1B，其他元器件参数如图9所示。

理论上方波信号的最高频率为无穷大，但根据频谱图可知其分量的振幅是随频率增加而逐渐衰减的，这里不妨令其最高频率[fm=7f0]，即[fm=7KHz]。分别改变图9电路中周期性脉冲信号频率（即抽样频率）、滤波器截止频率（通过改变双联调电位器[R1]、[R2]的阻值），得到如表1所示的结果。

在前述假定[fm=7KHz]情况下，若[fs=10KHz]，则显然[fs<2fm]，不满足抽样定理，抽样后频谱发生混叠，方波的恢复情况如表1的第一次测量结果。

若[fs=16KHz]，则[fs>2fm]满足抽样定理，且[fc=8KHz]也满足[fm≤fc

若[fs=16KHz]，[fc=12KHz]，虽然满足[fs>2fm]但不满足[fm≤fc

3.2 三角波的抽样与恢复

三角波的抽样与恢复电路完全同方波，只是将信号源的方波改成三角波即可。这里同样设三角波的最高频率[fm=7f0]，即[fm=7KHz]。然后做如表1一样的三次测量，得到如表2的结果。

如同方波的抽样与恢复，三角波的抽样与恢复也存在混叠失真和镜像失真。但因为三角波的分量随频率增加，其幅度衰减速度要大于方波，所以同样设置[fm=7KHz]情况下，三角波混叠失真要小得多，比如表2的第二次测量，在同样条件[fs>2fm]和[fm≤fc

4 结论

抽样定理是信号与系统课程重要的内容，一般都会在该课程的实验课里开设这个定理的验证实验，但多数是硬件实验，即电路已经设计好，基本上连接导线就完成了实验，从而导致对定理本身并没有很好理解和掌握。该文从频谱分析到电路设计，然后再通过Multisim软件搭建虚拟电路、设计实验条件，最后给出仿真结果并结合原理解释实验现象，通过较固定的硬件电路既灵活方便又安全可靠，既加深了对专业知识的理解又锻炼了电路设计的能力，既可作为独立的实验项目又可作为硬件实验的补充，类似的其他电路实验也可以这样完成。

参考文献：

[1] 吕波，王敏.Multisim 14电路设计与仿真[M].北京：机械工业出版社，2016.

[2] 张辉，何春燕，王玮.Multisim在模拟电路和数字电路课程中的应用[J].电子制作，2021（4）：17-19.

[3] 冷文，刘高华.Multisim在单管放大电路失真分析中的验证和辅助作用[J].实验科学与技术，2021，19（3）：106-111.

[4] 陈后金.信号与系统[M].3版.北京：高等教育出版社，2020.

[5] 康华光，华中科技大学电子技术课程组.电子技术基础-模拟部分[M].5版.北京：高等教育出版社，2006.

[6] 童诗白，华成英.模拟电子技术基础[M].5版.北京：高等教育出版社，2015.

【通联编辑：梁书】