船厂管子车间的新CONWIP控制系统设计

何 磊，王 岳

(江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003)

0 引 言

现代化的船厂管子车间已逐渐从加工车间(Job Shop,JS)生产转型为流水车间(Flow Shop,FS)生产，一些具备能力的管子JS已实现混合流水车间(Hybrid flow shop,HFS)的生产加工模式[1]。HFS往往在加工时间较长的工序安排更多的工位，加工时间较少的工序安排更少的工位，因此能在一定程度上避免生产过程中发生工位阻塞和工位空闲的情况。但仅仅只是工位的增加而不采取符合船厂管子HFS生产模式的生产控制系统，则难以实现降低产品生产周期、提高产品产出速率及维持工位负荷平衡等目标。

传统生产控制系统，例如看板管理(Kanban)和定量在制品法(Constant Work-In-Process,CONWIP)，在处理船厂管子这种加工时间可变性大的订单时都不能有效解决各工位间的负荷平衡问题；此外，这2种控制系统的研究对象通常并非HFS[2]。近年来，THÜRER等[3]提出一种能够控制工位间负荷平衡的卡片导航平衡控制(Control of Balance by Card Based Navigation,COBACABANA)系统，该系统在生产领域主要运用于JS，在FS的有效性[4]方面也有文献加以探讨，但未曾有文献证实该系统在HFS中是否有效。综合考虑上述控制系统的优缺点，结合船用管件的加工特点，以某船厂管子HFS为研究对象，对CONWIP的环路设置方案进行改进，提出以工序为单位对同一工序的工位纵向设置环路；在此基础上，融合COBACABANA系统的思想，设置工位负荷平衡表和订单池，从而控制各工位的负荷平衡。最后，通过在仿真软件中建模并加载不同控制系统进行试验和对比，验证新控制系统在控制工位负荷平衡方面的有效性及优越性。

1 新控制系统描述

1.1 基于HFS的CONWIP改进方案

CONWIP由SPEARMAN等[5]提出，该系统通过从FS中选择一条出口工位到入口工位的反馈环路来限制环路中的在制品数量，从而实现环路中系统的负荷控制。CONWIP能够很好地解决生产系统内在制品的控制问题，然而面对船厂管子生产这一多品种、小批量、加工时间可变性大的柔性生产模式却不具备工位间的负荷平衡能力，因为该系统仅仅只是在加工时间可变性较小的情况下控制环路中系统的负荷，并不考虑单个工位的负荷平衡。对于FS，即每道工序只含1个工位的流水线，当面对加工时间可变性较大的船厂管子时，则可能由于不同管子或同一管子的不同工序导致加工时间差距较大，出现大量管子堵塞于某一工序或者某一工序长期空闲的状态。传统CONWIP解决这一问题的有效方法只能是不断缩小环路中工序的数量，但环路中工序数越少就越接近Kanban控制系统，当环路只含有1道工序时即为Kanban控制系统[6]。

船厂管子HFS根据管子生产的特点，在不同工序设置不同数量的工位，可以有效避免由于工位不足而造成的工位堵塞现象，但由于没有对生产系统内的在制品数量进行有效控制，造成在制品积压，不仅增加现场管理工作的负担，也延长产品的生产周期[7]。通常，CONWIP在FS中以横向设置环路的方式来控制不同工序的在制品数量[8]，而在HFS中的在制品，在前道工序完工后可以选择后道工序的任何空闲工位进行加工，所以不适用于横向设置CONWIP环路。因此，以工序为单位纵向设置环路，环路设置可以是包含1道工序的单工序环路，也可以是包含多道工序的多工序环路，1条混合流水线可以设置1个环路，也可以设置多个环路[9]。环路设置方式如图1所示，假设该HFS有n道工序，每道工序有k个并行工位，其中Mi,j代表第i道工序的第j个工位。

图1 基于纵向CONWIP环路设置的HFS

1.2 考虑工位负荷平衡的新CONWIP控制系统

该方案对每道工序设置1个订单池和该工序各工位的负荷平衡表。订单池存放按加工顺序排列的投放卡；各工位的负荷平衡表显示工位的实时负荷情况。理论上，每张投放卡的大小由工件在该工序加工时间的大小按比例缩小后决定。当工件在该工位加工完成后便将投放卡取出，放置在代表该工位的负荷平衡表中，如此该工位在每加工完1个工件后就累加1张大小代表工件加工时长的投放卡，直到最后1个工件达到或刚刚超过工位设定的负荷最大界限，就关闭该工位不再接收工件。订单池和工位负荷平衡表的具体原理如图2所示。实际操作中，投放卡可以记录工件的加工时间和其他需要附加的生产信息，每当1个工件开始进入该工序的某个工位，就把该工件对应的投放卡放置在工件上。加工完成后，将带有加工时长信息的投放卡取下，在计算机端输入相应的加工工时，直接在电子屏幕或者电子看板上显示该工位工时累加的过程。

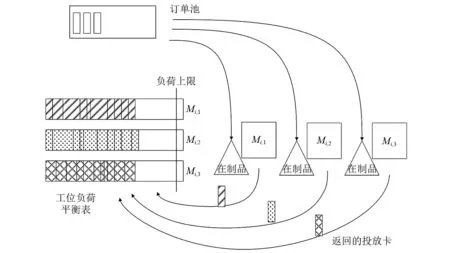
图2 某工序的订单池与工位负荷平衡表

其中，各工位加工工时负荷的上限，基于按工位性能平均分摊的思想并根据每批待加工工件的加工工时，由式(1)决定：

(1)

式中：Si为工序i的工位总数；Ti为生产计划中所有工件在工序i的加工时长；δi,j为工序i中工位j的加工性能系数；Li,j为工序i中工位j的负荷上限时长。

2 船厂管子HFS仿真

2.1 船厂管子HFS建模及环路设定

以某船厂管子HFS为例，使用生产仿真软件Plant Simulation 12建立无控制系统、传统CONWIP控制系统和新CONWIP控制系统等3种模型，各控制系统的工艺流程相同。图3为考虑工位负荷平衡的纵向CONWIP环路模型。在HFS中，管子只能从初始工序进入，从最后一道工序离开，并严格按照工序进行加工，每个工件在每道工序只需选择1个工位加工，加工完成后即可移动至后道工序，每个工位1次只能加工1个工件[10]。工件的加工原则是先到先加工，依次优先分配给空闲机器。假定各工位加工能力相同，且不考虑机器故障率和机器的休息时间。

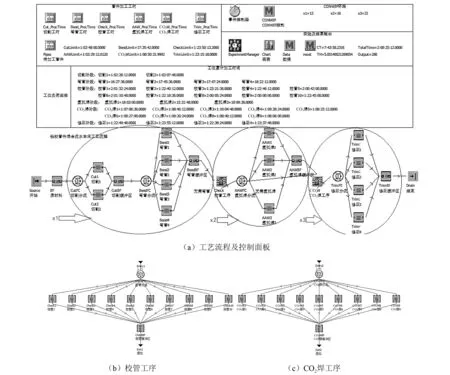
图3 船厂管子HFS仿真模型

随机选取某批管子订单共286根，按照排产顺序进行仿真。表1中显示部分待加工管子的加工工时信息。

表1 部分待加工管子在各工序的额定工时 h

待加工的管子在各工序的总加工时长分别为：切割，53 h 36 min；弯管，70 h 22 min 48 s；校管，478 h 22 min 12 s；氩弧焊，82 h 27 min 36 s；CO2焊，295 h 34 min 48 s；修正，189 h 1 min 12 s。综合考虑各工序工位数量及管子在各工序的平均加工时间后，将切割工序和弯管工序设置为环路1，校管工序和氩弧焊工序设置为环路2，CO2焊工序和修正工序设置为环路3，共3条环路。

2.2 仿真模型参数设置

CONWIP环路需要输入每个工序纵向环路的最大在制品数量。如图3(a)所示，x1、x2、x3分别为环路1、环路2、环路3的最大在制品数量。在此基础上，考虑各工位负荷平衡的CONWIP环路需要输入上述工序各工位的负荷上限时间，各工序的限定值对应模型的输入变量依次为CutLimit、BendLimit、CheckLimit、AAWLimit、CO2WLimit、TrimLimit。考虑每道工序各工位的生产能力相同，因此根据式(1)及各工序的总加工时间得出各工序的负荷上限值分别为：切割，26 h 48 min；弯管，17 h 35 min 42 s；校管，47 h 50 min 13 s；氩弧焊，27 h 29 min 12 s；CO2焊，32 h 50 min 32 s；修正，47 h 15 min 18 s。

3 仿真分析

3.1 仿真试验设计

规定无控制系统为方案1，传统CONWIP控制系统为方案2，考虑工位负荷平衡的新CONWIP控制系统为方案3。需要分析的仿真结果包括：产品产出速率(TH)；产品平均生产周期(CT)；总产量(Output)；全部工件完工时间(TotalTime)；各工位的负荷(WorkLoad)。对于方案2和方案3，为分析各环路中不同在制品数量对模型输出结果的影响，运用仿真软件中基于试验设计(Design of Experiment,DOE)理论的Experiment Manager(试验管理器)来定义试验。

船厂HFS每道工序包含多个并行工位，环路中在制品数量可根据工位数量进行设置，因此在试验时设置环路1的在制品数量从6开始，以1个工件为增量增至16；环路2的在制品数量从13开始，以1个工件为增量增至23；环路3的在制品数量从14开始，以1个工件为增量增至24。即，x1的取值范围为6～16，x2的取值范围为13～23，x3的取值范围为14～24，共计1 331场试验。

3.2 各控制系统对比与分析

对各方案的仿真结果进行汇总和统计。方案1的TH为5根/h，CT为28.3 h，TotalTime为2.4 d。方案2的TH最优值为5.2根/h，最差值为4.9根/h；CT最优值为6 h，最差值为9.2 h；TotalTime最优值为2.3 d，最差值为2.4 d。方案3的TH最优值为5.1根/h，最差值为4.5根/h；CT最优值为5.8 h，最差值为9.1 h；TotalTime最优值为2.3 d，最差值为2.6 d。

以方案2和方案3的CT为例，绘制如图4所示的散点图进行分析，可以发现：方案3在各试验场次的CT结果总体优于方案2。随着在制品投入量的增加，2种方案的CT值呈现出逐渐增大的趋势。这表明在制品的数量应该控制在一个较低的范围，才能缩短生产系统内在制品的等待时间。

为确定方案3在控制工位负荷平衡方面的有效性，随机选取方案2和方案3中结果较为接近的试验场次Exp 889进行分析。各方案的仿真结果如表2所示，工位负荷情况如图5所示。

由图5可以发现：在方案3控制下的各工序工位负荷总体趋于平稳；在切割工序中，方案3的工位负荷最为平衡，其次为方案1，最差为方案2；在弯管工序中，方案1与方案3的工位负荷平衡能力相当，都优于方案2；在校管工序中，方案1的工位负荷最为平衡，其次为方案2和方案3；在氩弧焊工序中，方案3的工位负荷最为平衡，其次为方案2，最差为方案1；在CO2焊工序中，方案3的工位负荷最为平衡，其次为方案1，最差为方案2；在修正工序中，方案1的工位负荷最为平衡，其次为方案3和方案2。

图4 方案2和方案3的CT曲线

由上述仿真结果发现：当设定环路使生产系统内在制品数量维持在合理范围时，方案2和方案3的CT、TH、TotalTime指标均优于方案1；方案2的TH和TotalTime指标略优于方案3；方案3的CT、WorkLoad指标总体优于方案2。这表明：当考虑CT和WorkLoad为最优目标时，采用方案3进行生产控制能取得更好的效果。

表2 各方案的仿真结果

图5 各方案的工位负荷对比

4 结 语

所设计的新CONWIP控制系统方案通过试验设计和仿真验证，整体反映出在总加工时间和产出速率保持小范围浮动的情况下，可以有效降低船厂管子HFS的产品平均生产周期并保持各工位的负荷平衡，有利于缓解工位阻滞现象，提升有效作业时间占比，使生产更为精益化。

传统CONWIP控制系统结构简单，对于多品种、小批量生产的HFS，其生产平衡难以保障，不符合船厂管子车间多工序、多工位生产的实际需求。新CONWIP控制系统方案扭转此局面，在保障工位负荷平衡和调控生产节拍等方面均有明显优势。然而，新方案在优化平均产出速率和总加工时间等方面仍有不足之处，今后可以对纵向环路的划分方法开展进一步研究，并结合新CONWIP控制系统方案，运用仿真技术在计划阶段准确预估系统的产能情况，为精益造船的深入推进提供新的有效途径。