小问题 2021-1

《小问题》栏目欢迎来稿出题(请自拟题目或注明题目来源)，题目及解答请寄《力学与实践》编辑部，采用后将致薄酬。

2021-1如图1 所示，已知平面上质点A 和B的运动rA(t)， rB(t)。C 点为A 和B 速度(速度大小不为零，方向不平行) 方向延线的交点。

(1) 求点C 的运动方程和速度；

(2)已知点A 的运动为rA(t)=ti+t2j/2，质点B 点质量为m，作用在B 上的作用力为f。若将随点A 运动的自然坐标系作为动系，求点B 的相对运动动力学方程；

(3)已知点A 的运动为rA(t)=ti+t2j/2，点B的运动为rB(t)=2ti+t2j/2，求点C 的加速度。(供稿：宝音贺西，清华大学航天航空学院)

图1

《小问题》栏目开展有奖竟答啦！2021 年4 月10 日前将题目解答发送到lxsj@cstam.org.cn，解答正确者即可获赠《力学与实践》2021 年第1 期期刊1 本(来信时请注明邮寄地址)。期待您的参与！

*《小问题》2020-6 解答*

问题：质量为m 的匀质矩形薄板ABCD，边长，且a ＞b，板可绕其位于水平位置的对角线AC 轴转动，轴承A、C 间的距离近似等于对角线长度。试用刚体定点运动知识：(1) 若板以匀角速度ω 转动(如图1 所示)，求板的动能及轴承A 和C 处的动反力；(2)若板在静止时，AC 轴上作用一力偶，力偶矩为M(如图2 所示)，求初瞬时板的角加速度及轴承A 和C 处的动反力。(问题及以下答案供稿：张孝祖，江苏大学)

图1

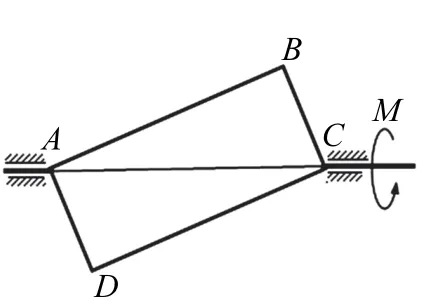
图2

解答：

(1)设想矩形板绕其质心O 作定点运动，如图3所示，建立板的惯性主轴坐标系Oxyz。

Oyz 为板平面，Ox 轴垂直于板面，i，j，k 分别为Ox 轴、Oy 轴及Oz 轴的单位矢量，板对Oy 轴及Oz 轴的转动惯量分别为

有几何关系

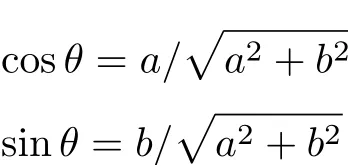
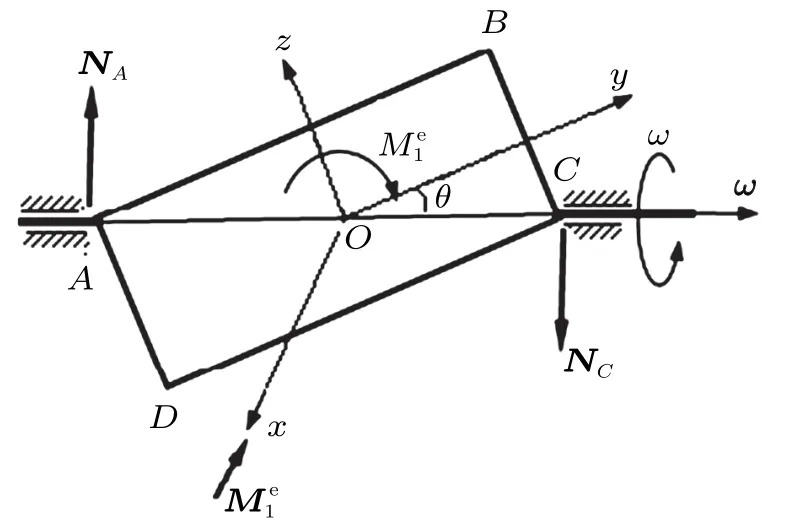
图3

板的角速度矢

板的动量矩

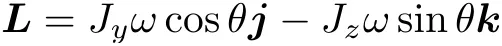
由动量矩定理，作用在板上的外力矩

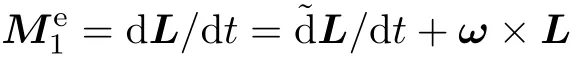
因为板匀角速度转动，故~dL/dt=0，而ω×L=ω2sin θ cos θ(Jy-Jz)i，代入计算，得

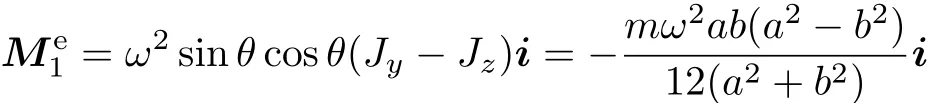
外力矩Me1由轴承A 和C 处的动反力NA和NC产生，NA和NC作用于板所在平面，方向垂直于AC 轴(见图3)，产生的力偶矩矢指向与Ox 轴相反，动反力大小

板的动能

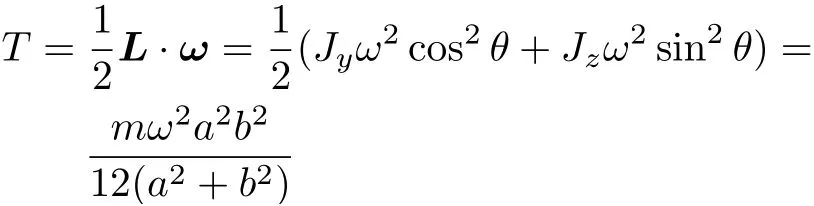
又因板绕AC 作定轴转动，动能T = JACω2/2，其中JAC为板绕AC 的转动惯量，上两式相比，可得

(2)参见图4，板绕AC 作定轴转动，有JACε=M，于是得板的角加速度

图4

仿 (1) 题的分析，作用在板上的外力矩 Me2=dL/dt = ~dL/dt+ω×L。注意到初瞬时板静止，角速度为0，故有ω×L=0，而~dL/dt=Jy˙ω cos θj-Jz˙ω sin θk=Jyε cos θj-Jzε sin θk。将有关量代入计算，得

在板面取ξ 轴垂直于AC，η 轴平行于AC，指向如图4 所示。

Me2在η 轴方向分量Me2η= M，此即为初瞬时AC 轴上作用的力偶矩。Me2在ξ 轴方向分量Me2ξ= M(a2-b2)/(2ab)，Me2ξ由轴承A 和C 处的动反力NAx和NCx产生，NAx和NCx方向垂直于板平面(见图4)，产生的力偶矩矢指向与ξ 轴一致，动反力大小为