旋转构件变形的完备性论证与分析1)

付靖宇 赵增辉，†，2)

*(山东科技大学能源与矿业工程学院，山东青岛266590)

†(矿业工程国家级实验教学示范中心山东科技大学，山东青岛266590)

问题处于重力场中的工程机械主机上安装的旋转部件如图1 所示：四根质量均为m、长度均为L的杆件以铰接构成菱形，竖直固定主轴与其一条对角线重合，菱形最上方的点被锁定而最下方的点是一个可在主轴上自由滑动的轴套且此两点间连接有一根刚度系数为k、自然长度为2L 的螺绕弹簧(密布缠绕在主轴上)。电动机驱动菱形结构绕主轴旋转，杆件与主轴夹角60°时体系达额定工作状态。忽略一切摩擦耗散。取k = 23mg/L，EI = Eb4/4。其中EI 是杆件的抗弯刚度。已知重力加速度g。

(1) 暂不考虑杆件的变形，求额定转速ω。

(2)当转速恒定于ω 时，只考虑杆件弯曲变形的影响，试计算∠OAO′相对于把杆件视为刚体的情况而言的变化量。

解答本题为第九届全国周培源大学生力学竞赛初赛试题，第(1)问基于刚体静力学和动静法给出解答，第(2)问的原解答首先通过作差分析得出两杆夹角变化量是惯性离心力载荷单独作用时杆件端截面转角的两倍。为此，需要求出杆件在惯性离心力这种线变载荷作用下的端截面转角。将实际载荷分布分解为以下两种分布的叠加：正对称均布载荷+ 反对称自相似线变载荷，如图2 所示。

图2 三角形载荷分解

该解法巧妙之处在于图2(b)情景下的端截面转角是常规的结论而无需计算，图2(c) 中点处亦可视为铰支座(由反对称性不难判定约束趋势)。因此可以利用线性叠加原理求出端截面转角。图2(c) 情景下的端截面转角必然与图2(a) 相似(成比例)，这样便可只通过一个方程直接解出答案。

笔者认为本题还存在一处细节值得思考，如图3 所示，设OA 两点连线与竖直方向的夹角为θ。在第二问求解中原解答只计算了杆件端截面转角Δα，这并非完整的角度变化量，还相差一项杆件与竖直固定主轴夹角的变化量Δβ，以下给出该问题的其他两种解答。

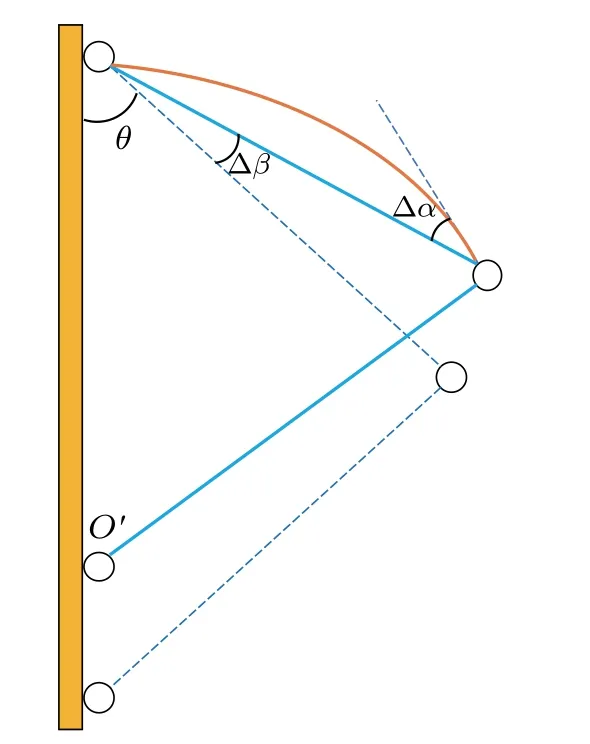
图3 杆件角度变化量示意图

第一种解法：基于拉格朗日分析力学。

暂不考虑弯曲变形，在随主机一起旋转的非惯性参考系中系统势能V 由以下三部分组成[1]

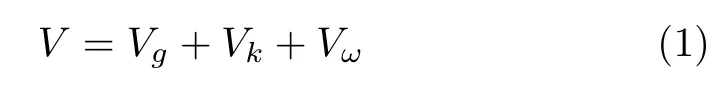
式中，重力势能Vg=-4mgL cos θ。

弹簧储存的弹性势能

惯性离心势能

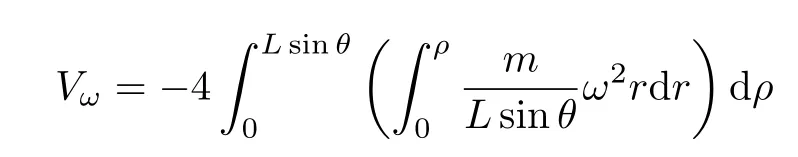
由式(1) 可得系统总势能

平衡状态势能取极值(即势能V 对θ 的导数为零)。由题意知θ =60°处为平衡点，所以

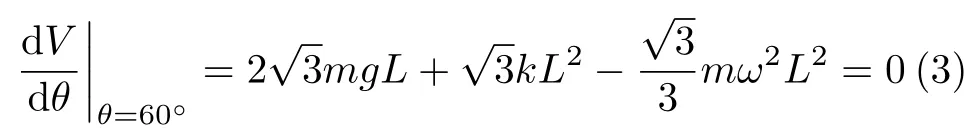
将式 (3) 代入 k = 23mg/L，即得主机旋转角速度

现在考虑弯曲变形的影响。记直线OA 与竖直方向的夹角为θ。如图4 所示，以O 点为坐标原点，沿着OA 方向建立x 轴，则OA 杆任意截面x 上的弯矩为

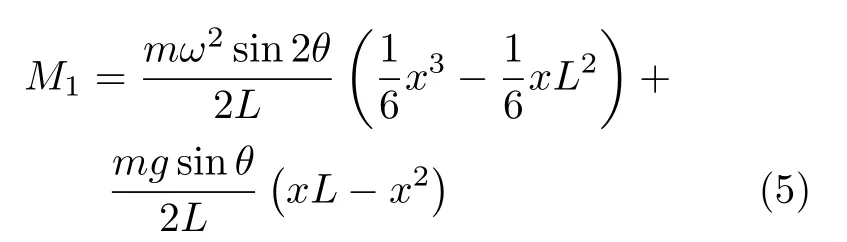
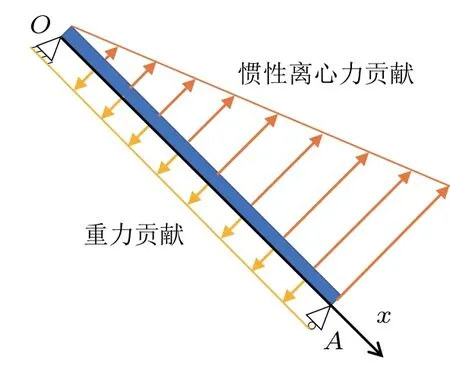
图4 杆件OA 受力图

同理，对于O′A 杆的弯矩方程为

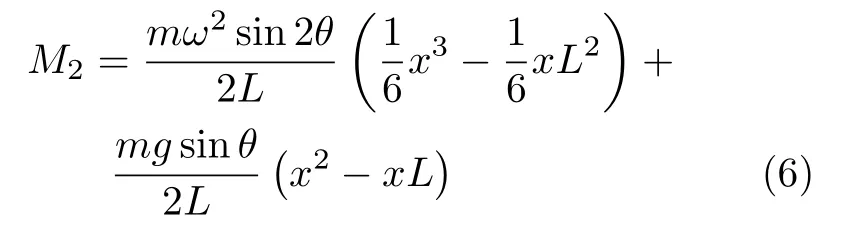
利用梁的挠曲轴微分方程和式(5)，可得OA 杆挠曲线解析式为

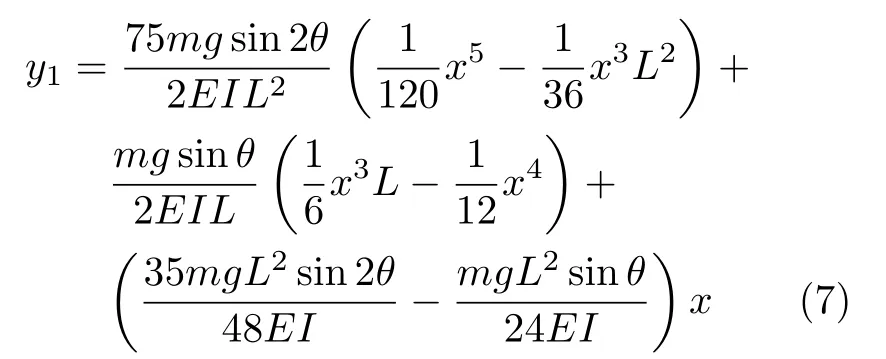
O′A 杆挠曲线的解析式为

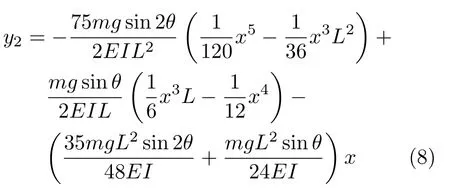
弯曲引起的系统惯性离心势能增量为

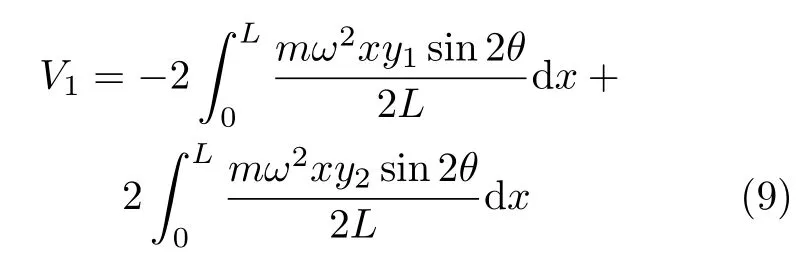
系统重力势能增量为

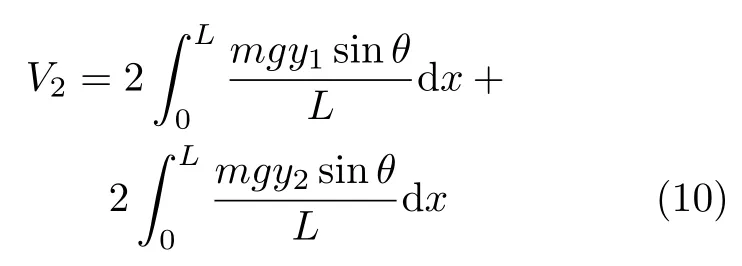
这是一个单自由度体系(挠曲线可看作一个以θ为参数的几何分布)。平衡态满足势能极值原理，即

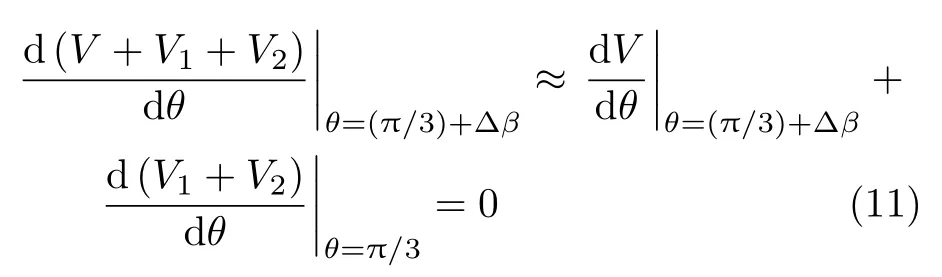
因为V1和V2自身就是比V 小一个量级的小量，所以式(11) 第二项导数在θ = π/3 处的值与在θ = Δβ + π/3 处的值相差二阶小量，故用前者近似代替了后者。将式(2)、式(9) 和式(10) 代入可计算出式(11) 中两个导数

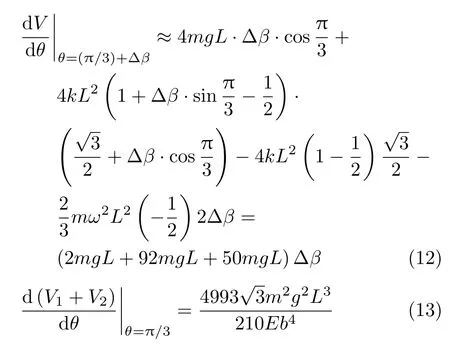
注意式 (12) 运用了展开到一阶小量的泰勒公式。

将式(12) 和式(13) 代入式(11) 可得直线OA与竖直方向夹角的变化量

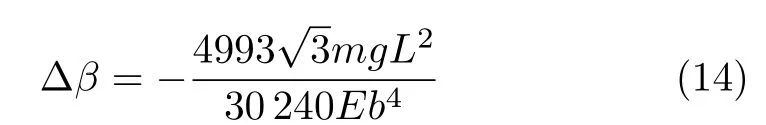
它实质上是由于为体系势能补加一项微小弯曲驱动能而引起的广义坐标θ 的平衡点的偏移。所以，由几何关系易知本题最终答案应该为

第二种解法：基于牛顿矢量力学。

上述基于能量解法，下面再利用牛顿矢量力学加以论证[2]。设OA 杆和O′A 承受的重力和惯性离心力对铰点O 和O′的力矩之和分别为T1和T2，则

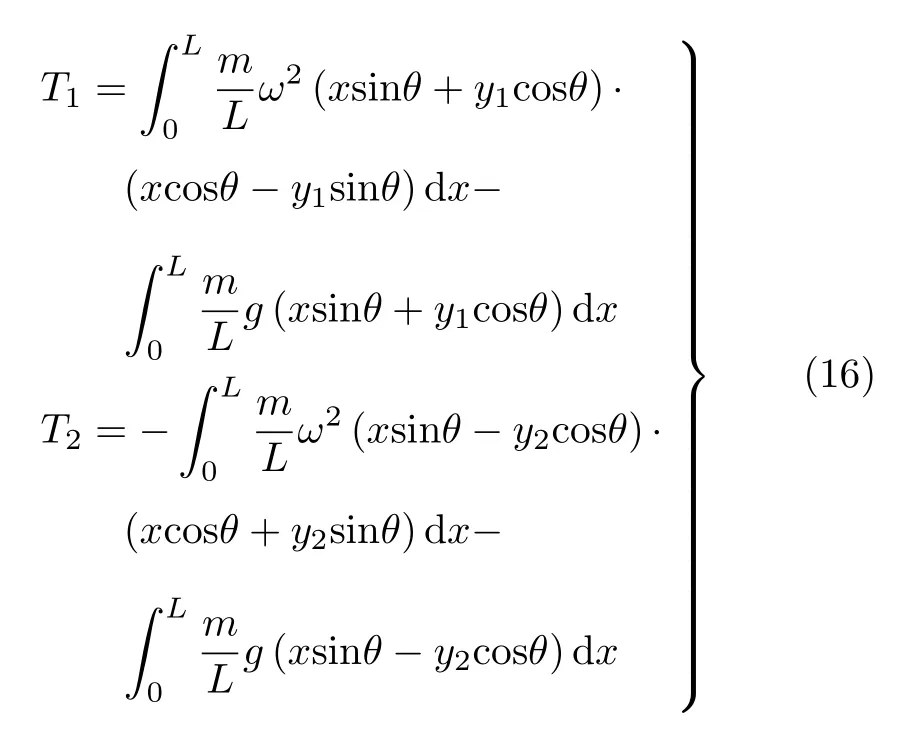
将式(7) 和式(8) 代入，略去二阶小量，得

设A 铰处对杆的约束反力为(fx，fy)，则对OA、O′A杆可列平衡方程

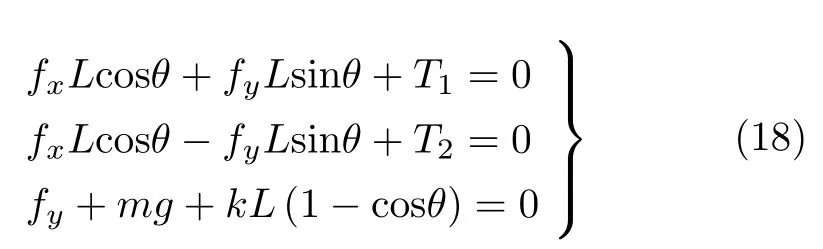
式(18)是关于θ 的三角方程组，不易直接得出θ。我们的目标是求以上3 个平衡方程中θ 相对60 度的偏移量。为此，令θ =π/3+Δβ，代入方程组并展开到关于Δβ 的一阶小量(系数中存在EI 的项无需展开，因为系数本身即是小量)。相对应地，约束反力也要写成零阶量附加一阶小量的形式。为此，可先求出约束反力的零阶量(即不考虑杆件变形时的约束反力值) 为

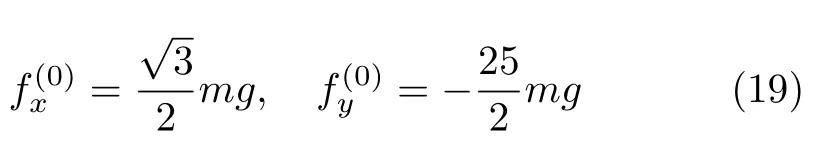
由此可得到最低阶近似后的线性方程组

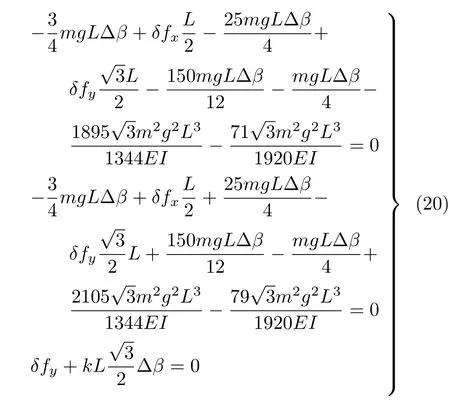
联立求解可得与式(14) 相同的解答。

最后讨论原解答的完备性。原解认为两杆夹角变化(指本文章中的Δα) 与重力无关，在书写弯矩方程时直接略去了重力力矩这一项，本文着重计算的修正角度是与重力相关的，文中式(5)和式(6)计入了重力以及受重力影响的支反力的贡献。

第二问原解答本文进一步补充了由于系统平衡点的偏移杆件角度的变化量Δβ，易知

这说明Δβ比Δα小一个数量级。从论证过程来看求解Δβ的过程显然比求解Δα的过程困难许多。因此，从数值量级来看是可以忽略Δβ的。该题作为全国大学生力学竞赛试题所给出的解答从本科生知识架构来讲是完全合理的。但从科学的严谨性角度考虑，本问题解答应更加完备。事实上，本题若控制额定转速为单一变量，即控制不考虑弯曲变形时杆件与竖直方向夹角θ为单一变量，可导出Δβ/Δα与θ的关系，进一步可讨论θ取哪些值时可以忽略Δβ，限于篇幅，不再讨论。