实心橡胶自行车胎动力学特性及影响因素分析
2021-03-05初红艳洪英洁
初红艳,王 瑞,陈 其,洪英洁
(先进制造技术北京市重点实验室,北京工业大学先进制造与智能技术研究所,北京100124)
1 引言
随着共享单车的逐渐发展,自行车越来越多样化,仅在轮胎这一方面,就存在许多差异,如材料的不同、实心与空心的区别以及尺寸的不同等。由于实心轮胎具有寿命比较长、不用打气、不怕扎胎等优点,所以市面上使用实心轮胎的自行车企业越来越多。除此之外,轮胎作为自行车的重要组成部分,其材料的选择和尺寸大小对它本身的使用寿命以及自行车的平稳运行至关重要。在实际工作状况下,由于其材料以及尺寸选择不当,会导致轮胎部分位置所承受应力应变过大,中心轴垂直方向跳动明显,从而使轮胎寿命减少和自行车运行稳定性降低,所以有必要针对自行车轮胎进行瞬态动力学仿真分析,以便得出比较合理的优化方案。
文献[1]运用拉格朗日微分方程研究自行车轮的运动状态,研究了车身转弯时处于倾斜状态,在重力作用下不致倾翻的问题;文献[2]研究了自行车稳定性传统理论受到质疑和新理论提出的过程,解释影响自行车稳定性的离心力效应、陀罗效应和新提出的脚轮效应的力学原理;文献[3]基于聚氨酯弹性体优异的性能,建立了不同密度的蜂巢式塑料轮胎模型,运用有限元软件分析了稳定滚动下轮胎的接地性能和应力分布;文献[4]以ANSYS Workbench软件为工具,分析了蜂巢轮胎静态工况下的承载能力和等效应力分布,得出该轮胎承载能力、接地印迹和等效应力分布均与蜂巢密度密切相关;文献[5]在合理假设的基础上建立了轮胎三维有限元分析模型,其中橡胶材料模拟为Mooney Rivlin 模型的超弹性材料,计算了不同载荷、速度条件下负重轮的应力-应变场,为负重轮实心轮胎的设计及其温度场的计算提供重要的理论依据。上述关于自行车稳定性的研究,多应用理论推导,对于轮胎与地面滚动接触的研究,大多为较大尺寸的汽车轮胎与地面的接触,关于实心自行车轮胎与地面接触研究较少。
本研究结合实心自行车轮胎的实际受载情况,实地测量某品牌自行车实心轮胎尺寸作为基准,利用ANSYS Workbench 瞬态动力学模块对其加载求解,得出轮胎应力、应变分布情况以及中心轴垂直方向的跳动。而后对不同材料、尺寸的轮胎进行仿真,得出材料、尺寸等因素对应力应变和稳定性的影响,对比结果得出优化方案。
2 自行车轮胎与地面有限元模型
2.1 自行车轮胎与地面的三维建模
自行车轮胎与地面滚动接触的结构简图,如图1 所示。主要由实心橡胶圈和地面组成,实测橡胶圈内径502mm,厚度25mm,地面尺寸分别为长8000mm,宽150mm,厚100mm。由于仿真中地面设置为刚体,其厚度对计算影响不大,长度、宽度保证轮胎稳定运行(3~4)s(1~4 圈)即可。在三维建模过程中,为了缩短ANSYS 仿真计算时间以及确保计算的准确性,只建立车轮橡胶圈部分的模型,省去了钢圈结构,其重量用向下的压力代替,由于只研究轮胎部分的应力、应变以及中心轴的跳动情况,故省略钢圈结构对试验结果影响不大。

图1 车轮与地面结构简图Fig.1 Schematic Diagram of Wheel and Ground Structure
2.2 自行车轮胎与地面有限元模型的建立
2.2.1 材料设置
在有限元分析之前,需要先定义材料参数,本研究通过将橡胶超弹模型和黏弹模型进行叠加,研究轮胎在行驶过程中的变形情况。其中用Moony-Rivlin 模型来表征超弹模型中大变形特性,经验公式表示为:

式中:C10、C01、D1—材料系数;为橡胶材料变化后体积比。
文献[6-7]给出橡胶等效弹性模量与超弹模型参数比C01/C10、橡胶材料硬度之间的关系,本研究所选用的邵氏硬度为40 和50 的橡胶材料C10、C01取值,如表1 所示。橡胶可以看作不可压缩材料,故J=1,近似取0 值,本次设定为0.000001。

表1 C10、C01 选定数据Tab.1 Selected Data of C10、C01
黏弹模型选用广义Maxwell 模型,采用Prony 级数形式拟合黏弹参数以表征橡胶黏弹特性。Prony 级数可表示为:

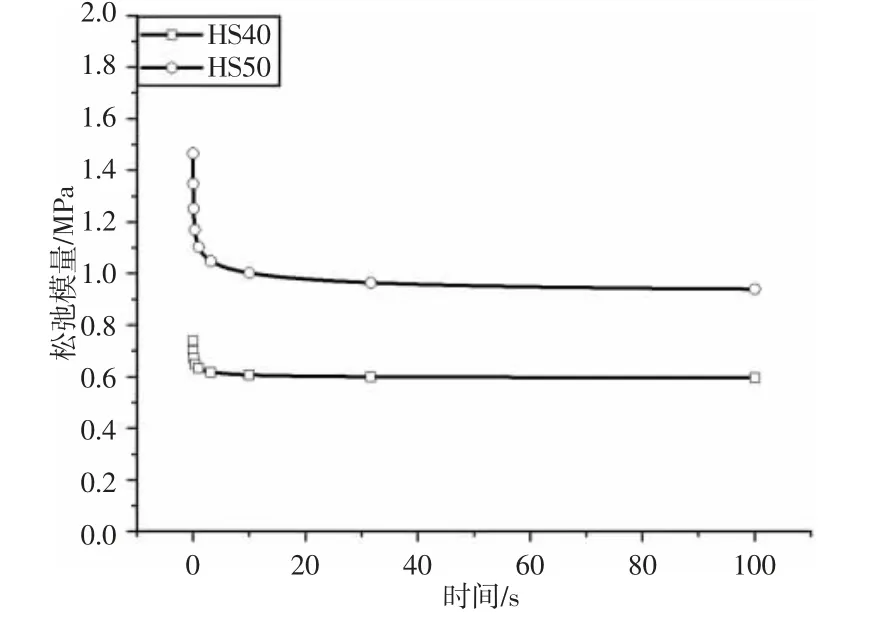
图2 HS40 和HS50 松弛曲线Fig.2 Relaxation Curves of HS40/HS50 Materials
由于地面刚度远远大于轮胎,因此可以用标准钢来定义地面材料。本研究共使用邵氏硬度40、邵氏硬度50 两种橡胶材料做仿真实验。运用SolidWorks 建模型后,将模型以“.x_t”导入ANSYS Workbench 中,选用自动网格划分法,设置网格尺寸时关联值为61,单元尺寸设置为默认,网格类型设置为四面体单元[9]。最终有限元模型,如图3 所示。
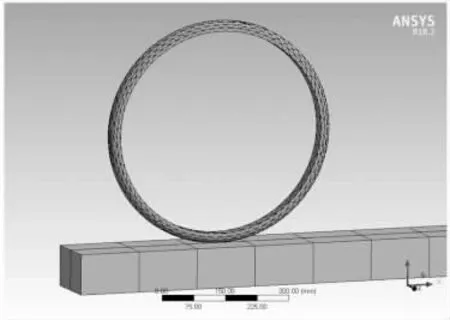
图3 有限元模型Fig.3 Finite Element Model
2.2.2 载荷与边界条件
设置轮胎中心轴处Z 方向位移为0 且可转动(以确保轮胎在Z 方向不产生滑动),X、Y 方向自由,对地面施加固定约束,如图3 所示。给轮胎施加向下压力400N(成人体重65kg 与自行车自重15kg 总和的一半)和5rad/s 的角速度,设置轮胎在(0~1)s 完成下压以及匀加速。考虑轮胎与地面的摩擦作用,摩擦系数设为0.2。
3 瞬态动力学特性分析
将所建模型进行瞬态动力学仿真,提取轮胎运动过程中最大等效应力、等效应变的值以及中心轴的跳动情况,表征轮胎稳定性的方法有很多种,此处我们用中心轴的跳动即其在竖直方向的位移来表征。在轮胎稳定运行1s 之后,可以提取中心轴在Y 方向的位移变化来表征它的跳动情况。此处以邵氏硬度50,速度5rad/s,内径502mm,厚度25mm 为例,此模型轮胎运行时间为4s(3.2 圈),最后时刻轮胎等效应力、等效应变云图,如图4、图5 所示。中心轴在Y 方向的位移,如图6 所示。

图4 等效应力云图Fig.4 Equivalent Stress Nephogram

图5 等效应变云图Fig.5 Equivalent Elastic Strain Nephogram
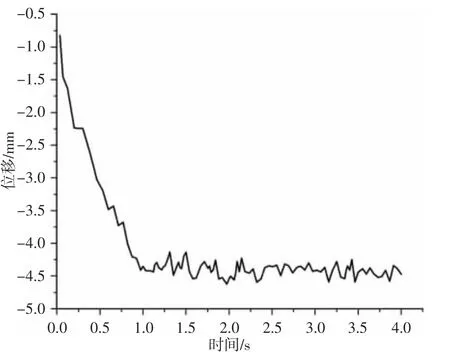
图6 中心轴在Y 方向位移Fig.6 The Central Axis Y-Displacement
在图4 与图5 中,为了方便观察自行车轮胎的变形,隐藏了地面的模型,提取其中等效应力、应变的最大值,可以看出最大应力与最大应变均发生在轮胎与地面接触处,最大应力为0.3612MPa,最大应变为0.1672。在图6 中,(0~1)s 由于力匀速增大下压,故位移越来越大。在其稳定运行后,位移量在4.1347mm 与4.62mm 之间波动。
4 轮胎影响因素分析
4.1 材料对轮胎的影响
材料对比的仿真结果,如表2 所示。其中位移方差为提取轮胎在1 秒以后的波动情况,即轮胎受力稳定后中心轴在Y 方向的位移方差,如图6 所示。
由表2 可知,在相同工况下,邵氏硬度40 的实心橡胶轮胎的最大应变普遍大于邵氏硬度50,最大应力则相反。由于橡胶材料硬度的提升,其抵抗变形的能力也随之增大,故得到以上结果。邵氏硬度40 的实心橡胶轮胎中心轴的位移方差普遍大于邵氏硬度50,说明随着橡胶硬度的提升,实心橡胶轮胎产生变形逐渐均匀,中心轴跳动变小,稳定性变优。

表2 影响因素对比Tab.2 Comparison of Influencing Factor
4.2 尺寸对轮胎的影响
为了研究轮胎尺寸的影响,从直径、厚度两个方面来做分析。
4.2.1 直径与厚度影响比重分析的正交试验设计
为识别轮胎尺寸中直径和厚度等因素对轮胎运行平稳性影响权重,以邵氏硬度50 的实心橡胶轮胎为例(因为硬度50 的材料性能较优),选用三水平三因素正交试验规划仿真,其中选用车轮行驶速度来作为第三因素来辅助完成试验,提取仿真计算值对优选参数等影响权重进行排序。正交试验所选因素及水平,如表3 所示。各因素取值范围以实测数据为基准做小范围变动[10]。

表3 试验因素水平表Tab.3 Table of Experiment Factors and Levels
试验设计好后,严格按照每个试验要求进行试验,对仿真结果做好记录。对没有列入正交试验表的因素(如橡胶材料参数等)要保持在固定状态,以便得到准确的试验对比结果。试验设计方案及其中邵氏硬度50 的最大应变试验结果,如表4 所示。

表4 试验设计及HS50 最大应变试验结果Tab.4 Design of Experiment and HS50 Maximum Strain Experiment Results
RA=max(KA1,KA2,KA3)-min(KA1,KA2,KA3),(RA 即为R 行、A 列对应数值,KA1 即为K1 行、A 列对应数值,KA2、KA3与KA1 类似);RB=max(KB1,KB2,KB3)-min(KB1,KB2,KB3),(RB,KB1,KB2,KB3 各含义同上),RC=max(KC1,KC2,KC3)-min(KC1,KC2,KC3),(RC,KC1,KC2,KC3 各含义同上)
在表4 中,KA1,KA2,KA3 的差异反映了因素A 三个水平(A1,A2,A3)的差异,其中KA1 最小,说明转速为3rad/s 时,最大应变值最小;KA3 最大,说明转速为7rad/s 时,最大应变值最大。KB1,KB2,KB3 的差异反映了因素B 三个水平(B1,B2,B3)的差异,其中KB3 最小,说明轮胎直径为527mm 时,最大应变值最小;KB2 最大,说明轮胎直径为502mm 时,最大应变值最大。KC1,KC2,KC3 的差异反映了因素C 三个水平(C1,C2,C3)的差异,其中KC3 最小,说明轮胎厚度为27.5mm 时,最大应变值最小;KC1 最大,说明轮胎厚度为22.5mm 时,最大应变值最大。
通常情况下,极差的大小反映了相应因素作用的大小。极差大的因素,意味着其不同的水平会给指标造成的差别比较大,通常是主要因素;而极差小的因素,意味着其不同的水平会给指标造成的差别比较小,一般是次要因素。本例中,按极差的大小,影响最大应变因素的主次顺序为C(厚度)、A(行驶速度)、B(轮胎直径)。用相同的方法找出其余指标的结果,如表5~表7 所示。
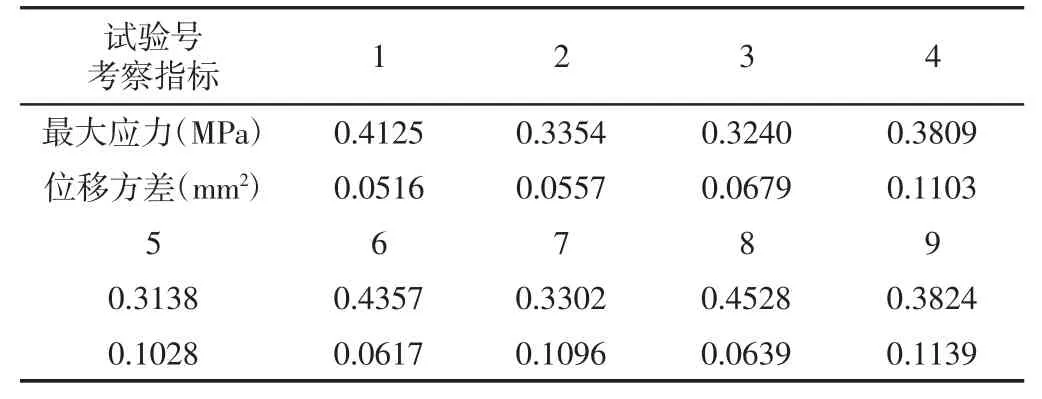
表5 其余两个指标试验结果Tab.5 The Other Two Indicator Experiment Results

表6 最大应力试验结果Tab.6 Maximum Stress Experiment Results

表7 位移方差试验结果Tab.7 Displacement Variance Experiment Results
由表5 至表7 可以得出轮胎厚度对应力、应变和位移的影响均比直径大。
4.2.2 厚度对轮胎性能的影响
次要因素与主要因素相比,对所要考察的指标影响较小,为了找出所考察指标与主要因素之间的关系,即轮胎最大应变、最大应力、中心轴位移分别与轮胎厚度之间的关系,需保持次要因素(行驶速度、轮胎直径)恒定不变,选择行驶速度3rad/s,轮胎直径502mm 作为固定不变值,在相同的工况下进行仿真,提取数据并对位移求方差,得出结果,如表8、图7 所示。

表8 HS50 不同厚度的仿真结果Tab.8 HS50 Simulation Results of Different Thickness
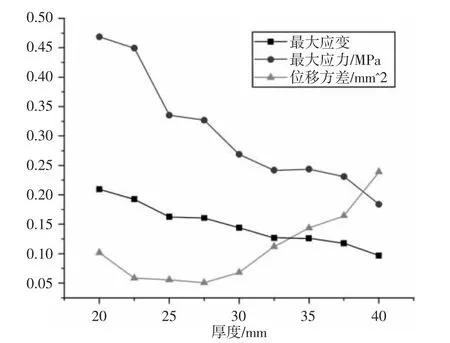
图7 考察指标与厚度的关系Fig.7 The Relation between Indexes and Thickness
从图7 可以看出,在轮胎厚度为(20~40)mm 区间内,随着轮胎厚度的增大,应力应变最大值逐渐减小;在中心轴位移方面,轮胎厚度为(20~27.5)mm 时,随着厚度增大位移方差整体为减小趋势,其中(22.5~27.5)mm 区间内,方差趋于稳定;在轮胎厚度为(22.5~27.5)mm 区间内,随着轮胎厚度的增大,中心轴位移方差逐渐增大,稳定性变差。在实际自行车轮胎设计中,为了延长其使用寿命,应力、应变以及中心轴在Y 方向的位移方差均不能过大,故轮胎厚度应在30mm 左右为宜。
4.2.3 直径对轮胎性能的影响
此处以邵氏硬度50 的轮胎为例,速度设为正常骑行速度约5rad/s,厚度为前文提到的某品牌自行车轮胎实测厚度25mm。结果,如表9 所示。

表9 直径试验结果表Tab.9 Table of Diameter Experiment Results
由表中5 组数据可以看出,在(452~552)mm 区间内,直径尺寸的改变对应力、应变以及中心轴在Y 方向的位移影响不大(与上一小节得出结论吻合)。
5 结论
本研究通过对不同材料、不同尺寸实心橡胶自行车轮胎和地面进行建模和瞬态动力学仿真,获得其最大应力、应变值以及中心轴跳动情况与轮胎材料、尺寸之间的关系,结论如下:
(1)在轮胎材料方面,对比邵氏硬度40 与50 两种硬度的橡胶,发现随着硬度的增大,轮胎抵抗变形的能力增大,故最大应力值增大,最大应变值减小且轮胎中心轴垂直方向跳动减弱。
(2)在轮胎厚度方面,橡胶材料硬度为50,在所测厚度25mm 左右,从图7 可以看出,在轮胎厚度为(20~40)mm 区间内,随着轮胎厚度的增大,应力应变最大值逐渐减小;在中心轴位移方面,轮胎厚度为(20~27.5)mm 时,随着厚度增大位移方差整体为减小趋势,其中(22.5~27.5)mm 区间内,方差趋于稳定;在轮胎厚度为(22.5~27.5)mm 区间内,随着轮胎厚度的增大,中心轴位移方差逐渐增大,稳定性变差。在实际自行车轮胎设计中,为了延长其使用寿命,应力、应变以及中心轴在Y 方向的位移方差均不能过大,故轮胎厚度应在30mm 左右为宜。
(3)在轮胎直径方面,橡胶材料硬度为50,在所测直径502mm 左右,发现直径尺寸在(452~552)mm 区间内的改变对应力、应变以及中心轴在Y 方向的位移影响不大。
(4)在设计实心橡胶自行车轮胎时,应优先考虑橡胶材料的选择,优先选择硬度较大的橡胶材料;其次考虑轮胎的厚度,较优的选择为30mm 左右为宜;最后考虑轮胎直径,直径尺寸的设计可更多的结合实际工况。
