一种适用于应急工程车液力传动匹配的逆向算法

贺福强，刘泰隆

（贵州大学机械工程学院，贵州 贵阳 550025）

1 引言

应急救援排障工程车是一种可以快速高效完成多种抢险救援任务的救援设备，对动力性能要求极高，有最大爬坡角度和最高时速要求指标。发动机与变矩器匹配是否合理是影响车辆动力性能的关键因素，目前工程车发动机与变矩器多采用低速大转矩匹配方案[1]。

国外匹配方式为首先确保整机协调，再解决发动机与变矩器匹配矛盾，如D.Ecarte 和A.GAneyne 设计了一种轮式工程车动力系统控制器，通过仿真利用该控制器调节动力系统能量对二者匹配进行优化。而国内为从二者匹配入手，继而考虑整机协调：如王国彪用数值方法计算二者匹配共同工作点；李春蒲与陈慧演利用N 分法、牛顿法、直接求根法求解其共同工作点。之后很多学者用数学分析，牛顿插值法等手段计算出评价参数，常绿提出了满意度函数，并基于满意度函数对二者匹配进行优化；高久好根据上述数值计算设计了匹配计算程序[2]。以上算法步骤均为首先根据车辆相关参数确定发动机型号，获取发动机外特性曲线，再由人为确定变矩器型号并获取原始特性曲线，利用多种算法计算两者共同工作点，获得共同工作输出特性曲线，根据匹配原则或评价参数等判断匹配是否合理，不合理则再次选取不同型号变矩器进行计算。但其存在以下问题：第一在选取变矩器型号时需要人为经验，导致误差较大，尤其面对新型发动机很难准确选择相应变矩器；其次如果匹配不合理，则需要多次循环计算，效率较低。为解决以上问题，提出一种适用于应急工程车的液力传动逆向匹配算法，该算法通过获得车辆指标及选取特殊工况进行计算，一次得出理想的变矩器原始特性曲线，据此优选出最合理的变矩器型号。为验证算法可行性，对实际车型进行计算，并搭建整车数学模型，通过Recurdyn 软件与Matlab/Simulink 软件对整车动力传动系统在两种极限工况下联合仿真，得出发动机和变矩器共同工作输出曲线，确定其满足车辆动力性指标要求。

2 逆向匹配算法

获取工程车参数，确定车身重量G（N），最大载重G′（N），最高速度Vmax（km/h），迎风面积A（m2），车轮半径rd（m），机械系统总传动比i 总（变速器，驱动桥、分动箱总传动比）六项必需参数。选择性获取风阻系数Cd（默认取1，正常空气密度ρ）、滚动阻力系数f（默认取0.02，为略旧轮胎在松软路面行驶阻力系数）[3]、传动效率η总以及转矩储备系数四项特殊参数，特殊参数可以参考默认值。

2.1 发动机选型及获取外特性曲线

首先用（1）式计算发动机功率理论值，选择发动机型号，并通过生产厂家获取发动机试验数据进行拟合，得到发动机外特性曲线。

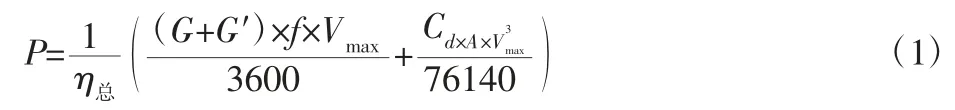
然后选取应急救援排障工程车的特殊工况，根据匹配原则确定相关工作参数，计算变矩器相关参数。

2.2 最高速行驶工况

以工程车最高速行驶作为第一个特殊工况点，匹配原则为高速行驶时变矩器锁住，高效率传递动力：变矩器处于闭锁状态，即车速V=Vmax（km/h），转速比i=1。

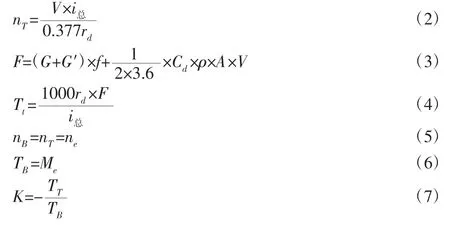
式中：nT—涡轮转速；F—整车牵引力（kN）；Tt—涡轮扭矩（Nm）；nB—泵轮转速（r/min）；ne—发动机转速（r/min）；TB—泵轮扭矩（Nm）；Me—发动机扭矩（Nm）；η—变矩器传动效率；λB—泵轮系数。

由此获得第一组i、K、η、λB数据。

2.3 最大牵引力工况

以整车牵引力最大状态为第二个特殊工况点，匹配原则为车辆起步瞬间，车速为零，负荷最大，理想情况为此时液力变矩器输入特征曲线经过发动机最大扭矩点。根据实验统计得出工程车起步加速度a 平均值0.4m/s2。工程车在松软路面最大爬坡角度上启动时整车牵引力最大，此时nT=0，i=0：

式中：μ—松软路面滑动摩擦系数（根据实验统计取0.6）[4]；θ—最大爬坡角度（根据工程车指标定义）。再根据上述式（4）、式（7）～式（9）求出K、η、λB。确定第二点对应数值。

2.4 效率最高工况点

以高效工作为第三种特殊工况，匹配原则为能够充分发挥柴油机的最大有效功率，使得变矩器的高效范围处于发动机的最大功率点附近[5]。根据工程车用变矩器一般原始特性曲线变化规律令i=0.7，取工程车在松软路面中速行驶工况，确定发动机最大功率点的转速与转矩。

式中：f松—松软路面滚动摩擦系数（根据实验取0.037）。

根据上述式（4）、式（7）～式（9）求出K、η、λB。确定第三点对应数值。

2.5 换挡点工况

以换挡点作为其余特殊工况点，匹配原则为车辆应具有良好的经济性，液力变矩器与发动机的共同工作行驶时换挡点应该靠近经济性换挡点附近。工程车档位数均大于等于7 档，根据经济性换挡原则，油耗最低点附近为最佳换挡点，根据以下公式确定各档位传动比及理论换挡速度V。

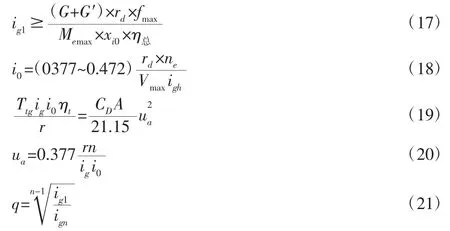
式中：ig1—一档减速比；i0—主减速比；q—各档位公比；Ttq—发动机最大扭矩；ig—最高档减速比。

根据发动机负荷特性曲线，确定油耗最低点发动机转速，再根据发动机外特性曲线确定该转速下的发动机扭矩，即ne、Me已知；

根据式（2）、式（4）、式（7）～式（9）、式（16）式求出i，K、η、λB、nT、Tt。确定各个换挡点时刻的i、K、η、λB。一共可以得出7 组以上数据。

对所得多组数据进行曲线拟合，获得变矩器特性曲线并以其为参考选择变矩器。

3 实例计算

项目提供的车型参数，如图1 所示。根据图中整车参数使用上述算法进行计算。

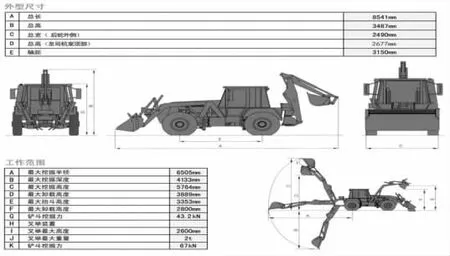
图1 整车参数Fig.1 Data of Vehicle

整车质量为20t，斗容为0.8m3，车轮半径约为0.6m，最大爬坡指标为30°，档位为8 档，土壤密度取1.5g/cm3，总机械传动效率取0.96，空气阻力系数取1（正常空气密度），车辆有效迎风面积按图1 尺寸参数进行估算，该车最大车速设计指标为大于90km/h，为保证动力性充足，按100km/h 进行计算。根据式（1）计算的发动机功率为205.28kW，初步确定型号为ISDe285-30，额定功率为210kw，最大扭矩为970Nm。液力传动油用8 号传动油，密度为860kg/m3，变矩器有效直径选择约0.8m。根据车辆参数及发动机参数通过式（17）～式（21）得主减速比为7.1，一档减速比为9.4，最高档传动比为0.7，各档位公比为1.45，最终得各档位传动比为i1=9.4，i2=6.5，i3=4.5，i4=3.1，i5=2.1，i6=1.4，i7=1，i8=0.7。如上文所述计算共获得表1 中的10 组数据。

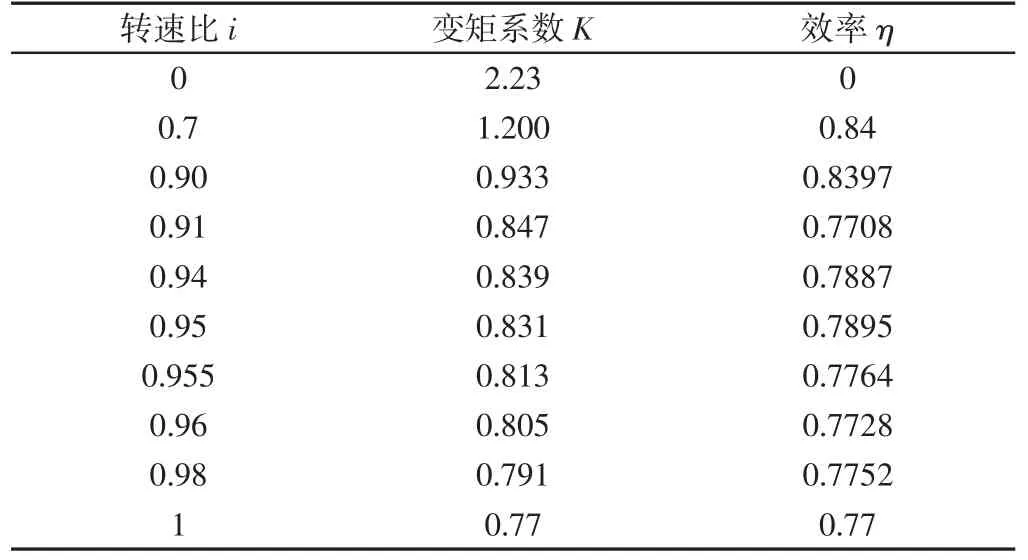
表1 计算结果数据Tab.1 Computational Data

将上表数据利用Matlab 进行曲线拟合，得出图2 曲线，并以此为根据选择变矩器，最终变矩器型号选择ME2842B 型变矩器，该型号变矩器原始特性曲线，如图3 所示。

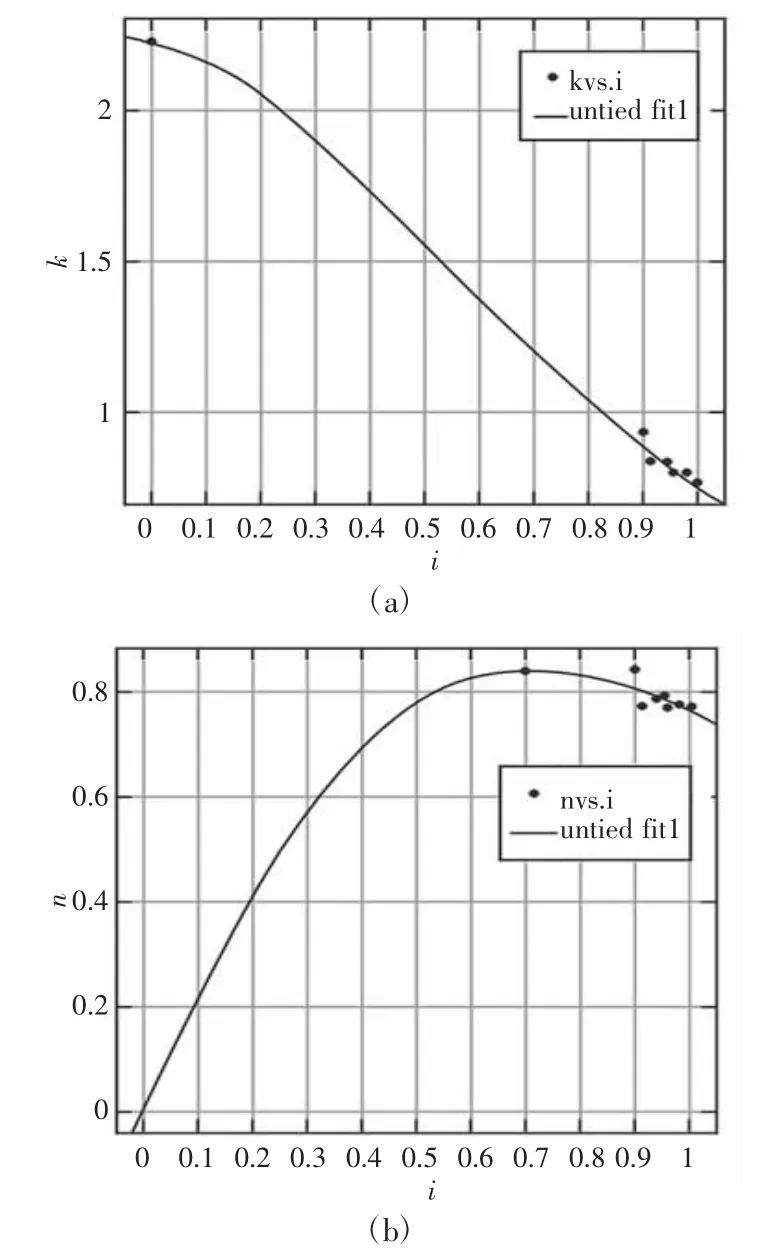
图2 理论变矩器原始特性曲线Fig.2 Theoretical Converter Primitive Characteristic Curve

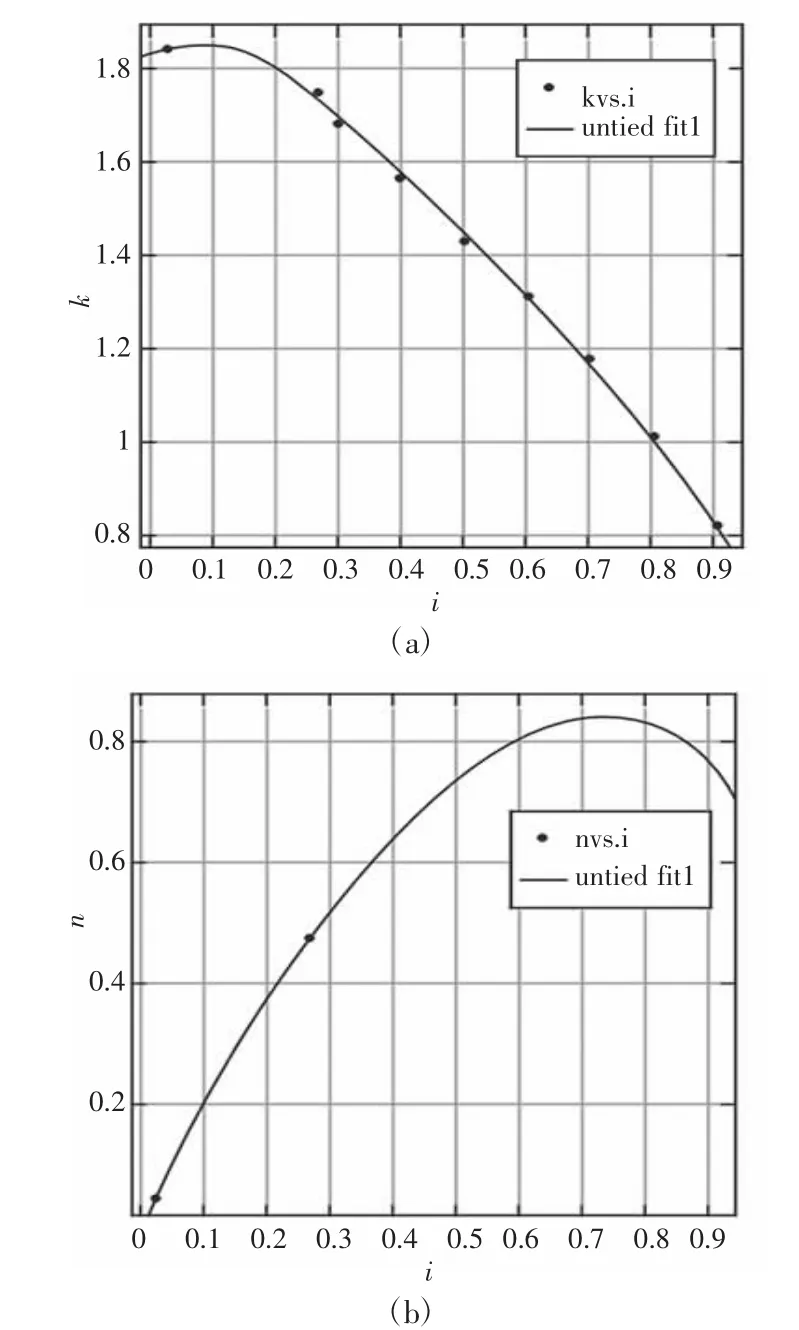
图3 ME2842B 型变矩器原始特性曲线Fig.3 Converter Primitive Characteristic Curve of ME2842B

4 仿真验证

为验证实例计算结果是否满足实际要求，建立整车数学模型及三维模型，将计算所得发动机与变矩器型号的参数输入模型中进行仿真。

4.1 柴油机数学模型建立

上述型号发动机转速与扭矩试验数据，如表2 所示。

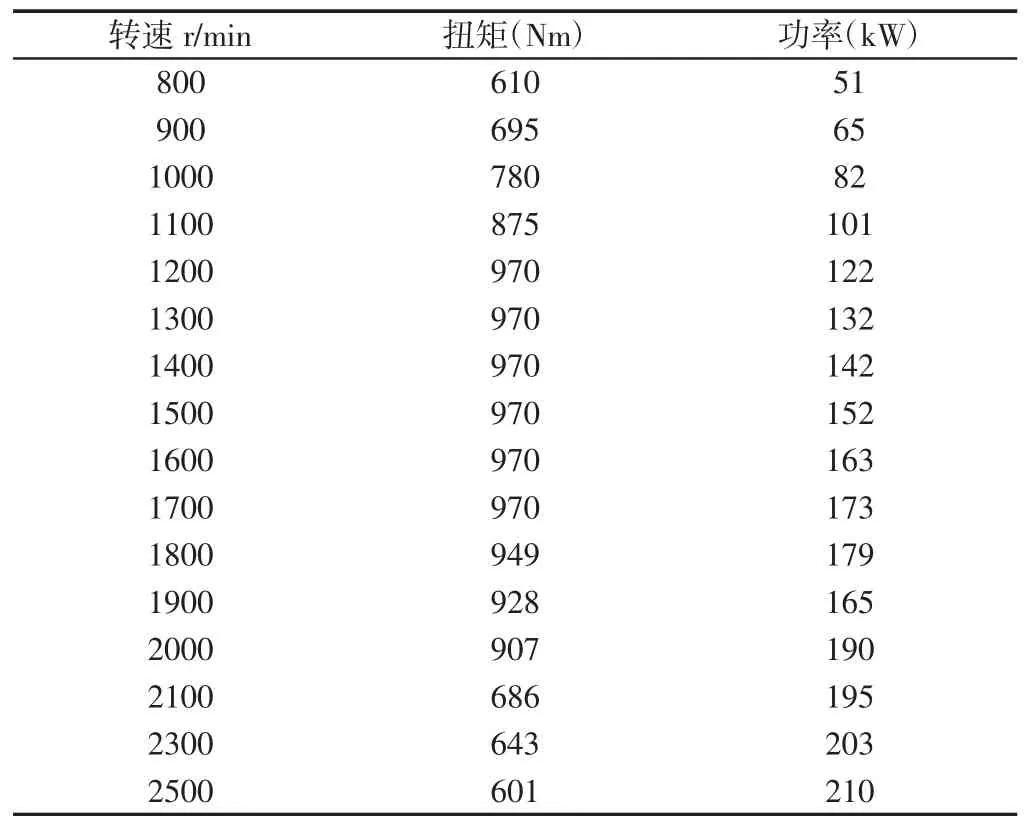
表2 ISDe285-30 型发动机外特性数据Tab.2 External Characteristic Data of ISDe285-30

对上表数据进行拟合，得到发动机外特性数学模型如下：

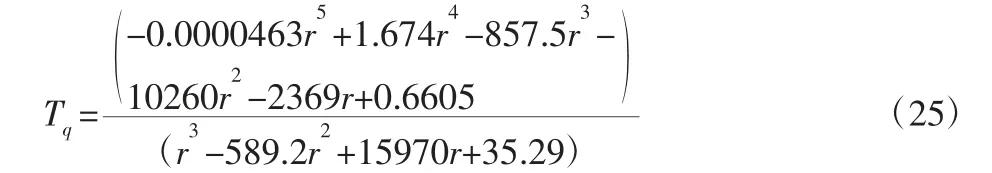
式中：Tq—发动机扭矩；r—发动机每分钟转速。

4.2 液力变矩器原始特性数学模型

原始特性曲线是由泵轮转矩系数、变矩系数、效率随着转速比变化的规律组成，这三个无因次特性曲线共同反映了液力变矩器的原始特性[6]。根据液力变矩器原始特性数据建立数学模型如下：

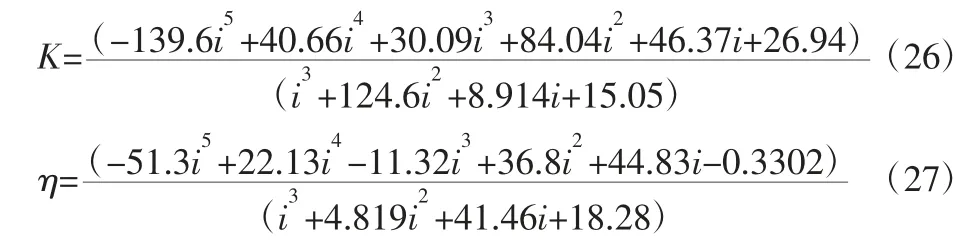
式中：K—变矩系数；η—变矩器效率；i—转速比。

4.3 车辆行驶方程

以车辆斜坡起步及最高速行驶两种极限工况作为研究对象。汽车行驶方程为：

式中：Ft起—起步驱动力；FtV—最高速行驶驱动力；Fd—滚动阻力；Fg—坡度阻力；Fj—加速阻力。其中空气阻力为：

坡度阻力为：

式中：α—坡度（deg）。

加速度阻力位：

式中：δ—汽车旋转质量换算系数。

滚动阻力部分采用基于土壤动力学所建立的弹性轮胎模型[7-8]，如图4 所示。

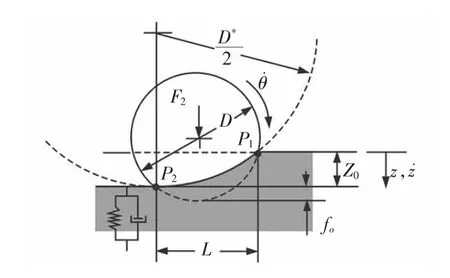
图4 土壤动力学-弹性轮胎模型Fig.4 Soil-Tire Model

车轮载荷与沉陷量关系如下：

运动阻力为：

剪切应力为：

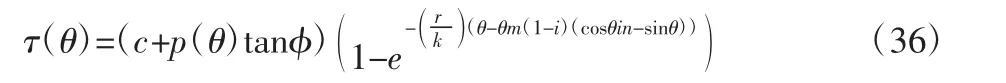
最终可求出滚动阻力合力为：

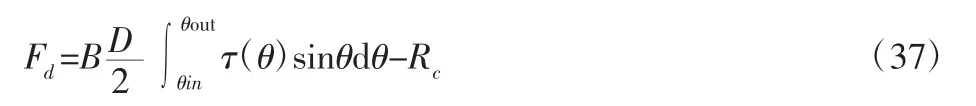
式中：B—轮胎宽度；D—轮胎直径；r—车轮半径；c—内聚力；φ—剪切角；K—剪切变形模量；i—滑移率；θ—轮胎与土壤接触角；kstat、kdyn、m、n—四个轮胎压力下沉参数；f0—轮胎形变；z0—下沉参数；Fz—车轮载荷；AA、BB—前后轮轮胎气压参数。

4.4 建模仿真及结果

液力传动仿真模型应用最为广泛的方法是应用Matlab 中Simulink 模块进行仿真[9]。但其忽略了行驶过程中滚动阻力系数变化问题，因此选择使用Simulink 分别搭建发动机与变矩器子模型并进行封装[10]，而Recurdyn 是目前比较快捷可以搭建土壤—弹性轮胎模型的软件，使用该软件搭建两种工况的车辆及道路模型，如图5 所示。Simulink 模型进行连接建立整车模型，如图6所示。

图5 行驶工况三维模型Fig.5 3D Model of Driving Conditions

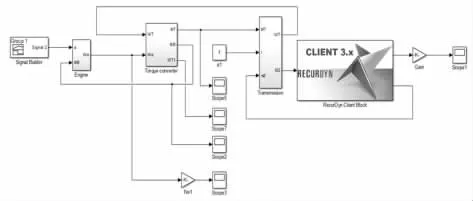
图6 整车联合仿真模型Fig.6 Co-Simulation Model of Vehcle

仿真初始条件为：油门开度线性增加，起步工况变速器为1挡传动比，最大车速工况取8 挡传动比，发动机初始转速为怠速转速800r/min，两种工况仿真时长分别为10s 和180s。仿真结果如下列各图。

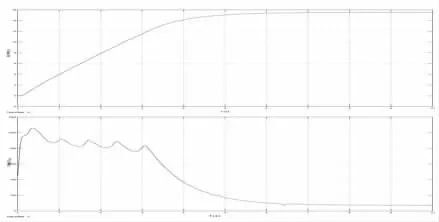
图7 起步工况车速与输出扭矩随时间变化曲线Fig.7 V-Time & T_T-Time at Starting

图8 高速工况车速与变矩器转速比随时间变化曲线Fig.8 V-Time & i-Time at High Speed

由仿真结果图7 知，30°坡度起步工况下，车辆起步瞬间变矩系数接近最大值，使输出扭矩在（900～1100）Nm 之间，接近该型号变矩器峰值。4s 时达到相对稳定速度。

最高速行驶状况下，从图8 可以看出车速可达100km/h，变矩器转速比及接近1，即变矩器为闭锁状态。

5 结论

（1）对发动机与液力变矩器的传统算法及匹配原则进行分析，针对其存在问题提出了适用于应急救援排障工程车的发动机和变矩器逆向匹配算法，提高了两者匹配的精确度与效率。

（2）获取实际工程车参数，应用新算法计算得出发动机与液力变矩器型号，建立数学模型并搭建仿真模型，应用Matlab/Simulink 和Recurdyn 软件联合仿真并输出结果。由仿真结果可知，当车辆起步瞬间变矩器低速大扭矩输出，使车辆在软土斜坡路况获得较大的起步加速度，短时间内车速达到平稳状态。在高速行驶状态下变矩器处于闭锁状态，将发动机转速直接传递到变速箱，车辆最高速度达到100km/h，满足应急救援排障工程车的特性。验证了此算法对于应急救援排障工程车的可行性，提高了该类工程车发动机与变矩器匹配的效率与准确度。