机械加工过程中轴承故障诊断方法研究
2021-03-05杨婧婷
杨婧婷
(沈阳航空航天大学工程训练中心,辽宁 沈阳 110136)
1 引言
在科技竞争日益激烈的当今世界,大型机械设备发展水平关系一个国家的综合实力和核心竞争力。轴承作为大型机械设备的关键零部件之一,其运行状态关乎整个设备的加工精度。当轴承发生故障时不仅影响加工效率,甚至造成人员伤亡,因此研究轴承故障诊断方法意义重大。
轴承故障诊断主要包括特征信号提取和故障类型辨识两个步骤[1]。特征信号可以分为时域、频域、时频域三类,其中时域特征信号有均值、标准差、均方根、偏度、鞘度、峰值因子等,频域特征信号有傅里叶频谱分析、高阶谱分析、解调谱分析等,时频域特征信号有短时傅里叶变换、小波变换、HHT 变换、局部均值分解等。故障类型辨识方法多种多样,包括专家系统[2]、故障树[3]、支持向量机[4]、神经网络[5]等方法。专家系统借助知识和数据库模仿专家推理过程[6],故障树通过逻辑图表逐层排查分析查找故障原因[7],支持向量机根据不同方法扩展为多类分类器用于故障类型识别[8],神经网络通过相互连接的神经元模拟脑神经,对故障类型进行识别[9],这些方法在不同应用领域都取得了较好的故障诊断结果,但依然没有形成普遍适用的成熟技术,轴承故障位置与故障类型的准确识别依然是当前研究的热点。
为了提高轴承故障诊断准确度,提出了新的能力算子,命名为解析能量算子。相比于Teager 能量算子,解析能量算子无需满足待解调信号瞬时频率和瞬时幅值的带宽远远小于载波这一条件,也不存在高阶近似误差和低阶近似误差。首先对原始信号进行EMD 分解,给出了IMF 分量筛选方法,计算各IMF 分量的解析能量谱样本熵作为特征参数;设计了支持向量机多分类器,经试验验证,基于解析能量谱样本熵的轴承故障诊断准确率达100%。
2 解析能量算子的提出
解调分析是轴承故障诊断中常用的信号处理方法,Teager能量算子解调方法在解调过程中存在低频误差分量和高频误差分量,要想获得较好的解调效果,要求待解调信号瞬时频率和瞬时幅值的带宽远远小于载波,而这一条件在实际故障信号中难以满足。为了解决这一问题,提出了解析能量算子。
2.1 Teager 能量算子及缺陷分析
Teager 能量算子一般记为ψ,对于实信号x(t),定义Teager 能量算子为:

下面使用Teager 能量分离算法估计出信号的瞬时幅值和频率。记任意的调幅调频信号x(t),其时变幅值为a(t),时变相位为φ(t),则x(t)=a(t)cos(φ(t)),将其代入式(1),得:

式中:第一项为期望成分,记为D(t),第二项与第三项为误差成分,记为E(t)。当待解调信号瞬时频率和瞬时幅值的带宽远远小于载波时,有ψ[a(t)]≈0、φ¨(t)≈0,此时E(t)≈0,那么式(2)可以简化为:

同理可求得x˙(t)能量算子为ψ[x(t)]=a2(t)ω2(t),联立式(3)得到瞬时幅值和瞬时频率估计值为:
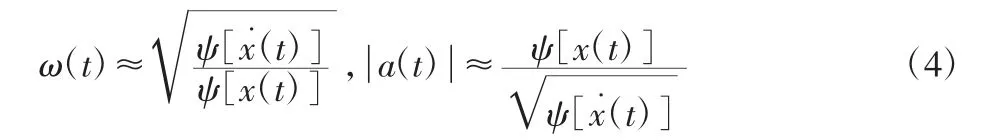
由以上推导过程可以看出,使用Teager 能量算子进行信号解调时,式(2)中出现了低频误差分量和高频误差分量,在满足待解调信号瞬时频率和瞬时幅值的带宽远远小于载波这一条件时,上述推导才能成立,否则就会产生极大的近似误差,而现实故障信号未必满足或难以满足这一条件。为了解决这一问题,提出了解析能量算子。
2.2 解析能量算子的提出

定义离散形式的瞬时幅值为a(n),瞬时相位为φ(n),瞬时角速度为Ω(n)=φ(n)-φ(n-1),则解析能量算子的离散形式为:

下面依据解析能量算子使用能量分离算法估计出信号的瞬时幅值和频率。为了方便计算,使用离散形式进行推导,令:

其中c(n)为:

将c(n)代入式(8),得:

得此信号的解析能量算子为:

将式中Ω(n-0.5)移动半个单位时间,有Ω(n)=Ω(n-0.5),联系式(8)和式(9)可得:

对比Teager 能量算子与解析能量算子的能量分离算法可知,Teager 能量算子在解调过程中,对式(2)的近似要求满足待解调信号瞬时频率和瞬时幅值的带宽远远小于载波这一前提条件,否则就会产生极大的近似误差。而解析能量算子在解调过程中,对R[s(n)]及c(n)的近似是基于数学原理的,不需要任何前提条件,因此提出的解析能量算子克服了Teager 能量算子的缺陷。
2.3 解析能量算子分析故障信号有效性验证
由式(6)可知,解析能量算子的输出为幅值平方与频率之积,与传统能量的定义相比,多乘了信号频率,由于故障信号中冲击信号瞬时频率较高,那么解析能量算子就能够更好地跟踪冲击瞬态特征。基于以上分析,提出基于解析能量算子的故障诊断方法为:首先计算信号的能量算子输出;而后对能量序列进行傅里叶变换,得到解析能量算子的能量谱;然后根据能量谱频率峰值和轴承故障特征频率判断轴承故障类型。

图1 外圈故障轴承振动信号Fig.1 Vibration Signal of Bearing with Outer Ring Fault
为了验证解析能量算子在轴承故障诊断中的有效性,在滚动轴承故障试验台上进行试验,轴承型号为6307E,为了模拟轴承外圈故障,使用激光切割机在轴承外圈切割出宽0.15mm 深0,13mm 的切槽。采集的轴承故障振动信号及其经过EMD 分解的第一个IMF1分量,如图1 所示。
分析两图波形可知,故障振动信号中出现了冲击特征,但是很不明显,无法明确判断是否发生故障,更无法判断故障类型。计算IMF1 分量信号的Hilbert 包络谱、Teager 能量谱和解析能量谱,结果如图2 所示。
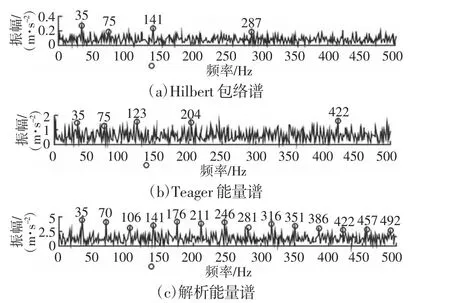
图2 IMF1 分量能量谱分析Fig.2 Energy Spectrum Analysis of IMF1
由IMF1 分量的包络谱和Teager 能量谱中可以看出外圈故障特征频率,但是其倍频信息无法提取;而解析能量谱中不仅可以提取35Hz 的外圈故障特征频率,而且其倍频阶次连续且明确,最高达到了14 阶,故障特征很直观也很明确,证明了提出的解析能量算子在故障诊断中的有效性。
3 特征参数提取及模式识别
滚动轴承故障诊断关键是从非平稳、非线性的振动信号中提取敏感特征信息,并依据敏感特征信息辨识出故障类型,在上节基础上,提出了基于解析能量谱样本熵的特征参数提取方法。
3.1 样本熵
以轴承正常状态、内圈故障、外圈故障三种状态为识别对象,正常状态时轴承的振动状态为随机振动,信号无规则所有熵值较大;当轴承出现故障时,振动信号中包含周期性冲击,信号自相似程度比随机振动高,因此轴承故障时熵值必然比正常状态小;对于外圈故障,由于轴承外圈不随轴转动,所以外圈故障振动信号更加规律,冲击特性更加明显,而内圈随轴转动,冲击特性的方向和幅值不断变化,所以内圈故障比外圈故障振动信号的熵值要大。
与近似熵相比,样本熵的计算不依赖数据长度,且其一致性更好,因此使用样本熵计算振动信号熵值。记原始数据序列为{x(1),x(2),L,x(N)},数据长度为N,则此数据序列样本熵计算方法为:
(1)设定嵌入维数m、相似容限r,将原始序列拆分为m 维向量Xm(i)={xm(i),xm(i+1),L,xm(N+i-m)},1≤i≤N-m+1;
(2)记任意两向量Xm(i)与Xm(j)距离为d[Xm(i),Xm(j)],将两向量距离定义为相应元素差值的最大值,即:
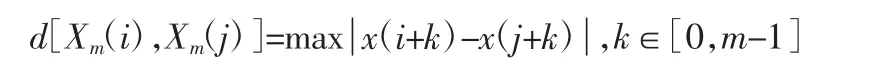
(3)对于给定的向量Xm(i),计算其与其余向量Xm(j)间的距离d[Xm(i),Xm(j)],i≠j。统计d[Xm(i),Xm(j)],i≠j 中小于r 的个数,记为Bi,定义:


(5)将维数增加为m+1,重复步骤(1)~步骤(4),得Bm+1(r),则样本熵定义为:
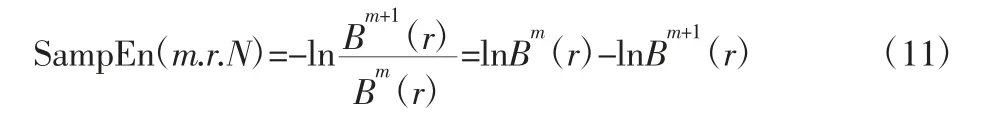
在这里,参数设置为m=2、r=0.2Std,其中Std 为原始数据标准差。
3.2 特征参数提取步骤
基于解析能量谱样本熵的特征参数提取方法为:首先对原始振动信号进行EMD 分解,得到各IMF 分量,依据规则对IMF分量进行筛选;对于筛选出的IMF 分量,计算其解析能量谱样本熵值作为模式识别的特征参数。
EMD 分解原理可以参考文献[10],在此不再赘述。主要给出IMF 分量的筛选方法。鞘度可以表征信号中的周期性冲击成分,因此鞘度越大则信号中的轴承故障信息越多,所有选择鞘度作为一个筛选条件;信号中的冲击成分越多则信号能量相对越大,所以能量也作为一个筛选条件;对于轴承故障信号,噪声分量或虚假分量与原始信号相关性极小,有效信号与原始信号相关性较大,因此选择各IMF 分量与原始信号相关性作为一个筛选条件。因此使用IMF 分量的鞘度Ku、能量E、与原始信号的相关度C 三者乘积作为指标对IMF 分量进行筛选,即:
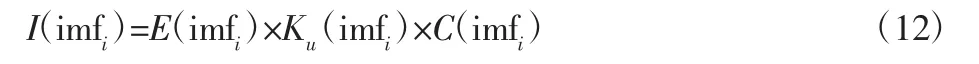
式中:I(imfi)—第i 个imf 分量的筛选指标。依据此指标筛选指标最大的前若干个分量。
3.3 故障模式识别
以支持向量机[11]为理论基础,构造了支持向量机多分类算法。当前较为成熟的支持向量机多分类算法包括有向无环图SVM 分类、投票法SVM 分类、二叉树SVM 分类等,由于二叉树SVM 分类依据输出首先为1 的支持向量机,判断故障类型,容易出现误判;而投票法依据每个支持向量机的输出,根据投票结果确定最终故障类型,出现误判的可能性很小,因此使用投票法SVM 分类器,其结构,如图3 所示。

图3 投票法支持向量机多分类器Fig.3 Support Vector Machine Multi-Classification by Voting
区分轴承的正常状态、内圈故障、外圈故障等三种状态,图中A 代表轴承正常状态,B 代表内圈故障,C 代表外圈故障。依据A、B 状态特征参数训练SVM1,依据A、C 状态特征参数训练SVM2,依据B、C 状态特征参数训练SVM3。而后综合每个支持向量机的输出判断故障类型。与二叉树SVM 分类相比,投票法中每个支持向量机都得到了充分利用,因此其误判概率极小。每个支持向量机输出为正(+1)时为第一个轴承状态,输出为负(-1)时为第二个轴承状态。
3.4 轴承故障诊断流程
依据以上分析,给出轴承故障诊断步骤为:(1)在轴承正常状态、内圈故障、外圈故障三种状态下分别采集振动信号,每种状态下采集N 个;(2)对每一数据样本进行EMD 分解,得到多个IMF分量,依据I(imfi)值筛选出前个IMF 分量;(3)计算每种状态下各样本中筛选出IMF 分量的解析能量谱,计算解析能量谱样本熵作为此状态下的特征向量,记为T=[SampEn1,SampEn2,L,SampEni],这样就得到了每种状态下的N 个特征向量;(4)使用每种状态下n 个特征向量用于训练支持向量机参数,得到三个支持向量机模型;(5)对其余特征向量进行故障模式辨识,根据每个支持向量机的输出结果确定故障类型。
给出轴承故障诊断流程,如图4 所示。

图4 轴承故障诊断流程图Fig.4 Bearing Fault Diagnosis Flow
4 实验验证
为了验证提出的解析能量算子在轴承故障诊断中更加有效,设计了滚动轴承故障试验台,如图5 所示。

图5 轴承故障试验台Fig.5 Bearing Fault Testbed
为了模拟轴承外圈故障和内圈故障,使用激光切割机在轴承外圈和内圈分别切割出宽0.15mm 深0.13mm 的切槽。使用加速度传感器敏感轴承振动信号,在轴承正常状态、内圈故障、外圈故障等状态下分别采集信号各100 组数据,对每种状态下振动信号EMD 分解后保留前4 个IMF 分量并计算其解析能量谱样本熵作为特征参数。
为了比较Teager 能量算子和解析能量算子在轴承故障诊断中的效果,从每种状态中任意抽取5 组数据,计算原始信号的Teager 能量谱样本熵和解析能量谱样本熵,再对5 组样本熵取平均值,其结果,如表1 所示。

表1 原始信号及前4个IMF 分量能量谱样本熵Tab.1 Energy Spectrum Sample Entropy of Original Signal and the Former 4 Order IMF Component
表1 中除了给出原始信号的Teager 能量谱样本熵和解析能量谱样本熵,还给出了前4 阶IMF 分量的解析能量谱样本熵。对比原始信号的Teager 能量谱样本熵和解析能量谱样本熵可以看出,Teager 能量谱样本熵虽然能够区分轴承正常状态、内圈故障和外圈故障,但是不同状态之间的熵值差远小于解析能量谱样本熵,这说明解析能量算子在轴承故障诊断中更加有效。
从表1 中各IMF 分量的解析能量谱样本熵可以看出,不同轴承状态下各分量信号的熵值差别明显,可以用于区分不同的轴承状态。为了进一步对比Teager 能量算子与解析能量算子在故障诊断中的效果,分别将Teager 能量谱样本熵和解析能量谱样本熵应用于支持向量机训练和分类,前50 组数据的特征参数用于训练,后50 组数据的特征参数用于模式识别。
随机从3 种轴承状态中各选取2 组数据,对支持向量机输出数据、投票结果和诊断结果进行说明。基于解析能量谱样本熵的支持向量机输出结果,如表2 所示。投票结果和诊断结果,如表3 所示。
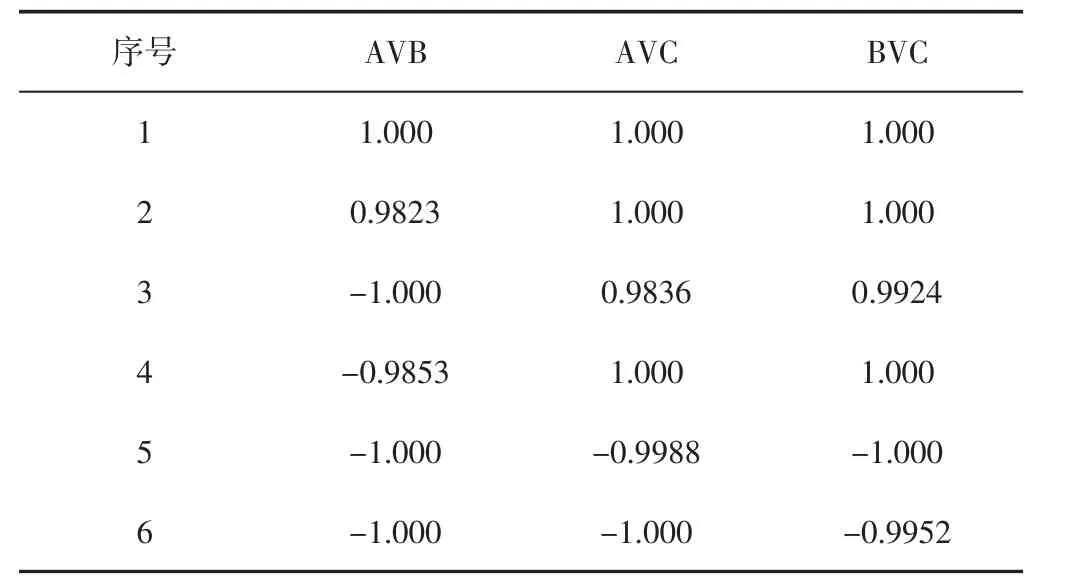
表2 基于解析能量谱样本熵的支持向量机输出Tab.2 SVM Output Based on Analysis Energy Spectrum Sample Entropy
表2 输出结果对应的投票和诊断结果,如表3 所示。

表3 投票结果与诊断结果Tab.3 Voting and Diagnosing Results
5 结论
经过讨论,得到以下结论:(1)提出的解析能量算子无需满足Teager 能量算子的使用条件,既不存在近似误差,又扩大了使用范围;(2)设计了支持向量机多分类器,经试验验证,解析能量算子在轴承故障诊断中的准确率远高于Teager 能量算子。
