带气膜阻尼悬臂平板的振动特性研究

张 鸿，崔东泽，邢海龙，王俊昌

（中国民航大学中欧航空工程师学院，天津300300）

1 引言

航空发动机叶片振动所导致的高周疲劳是造成航空发动机失效的关键因素之一，研究航空发动机的抑振技术不仅能够提高航空发动机的安全性，而且有助于延长航空发动机的维修周期，降低航空发动机的维护成本。

目前，能够有效抑制航空发动机叶片振动的阻尼技术共有四种[1-2]，分别是：干摩擦阻尼，约束层阻尼，冲击阻尼和气膜阻尼。其中，干摩擦阻尼和约束层阻尼为传统的被动式阻尼技术，目前应用广泛但各有缺陷：干摩擦阻尼技术成熟，但适用于较低阶模态；约束层阻尼通过设计能够有效控制不同频率内的振动，但在高离心力载荷下很难适用。冲击阻尼和气膜阻尼为先进的被动式阻尼技术，其中冲击阻尼抑振机理复杂，难以实现；而气膜阻尼结构简单、易于加工、且能对多阶振动进行有效抑制，被认为是在航空发动机叶片抑振方面具有应用前景的阻尼技术。

文献[3]通过气膜内流体运动压力的分布假设建立了粘性流体运动的气膜阻尼理论模型，着重研究了气膜压力和气膜厚度的对阻尼特性的影响；文献[4-8]建立了带气膜阻尼平板模型，并基于有限元对气膜阻尼系统（AFDS）的振动特性进行分析和研究；文献[9]基于平板振动理论建立了可压缩流体的AFDS 简化平板模型，文献[10]基于该模型推导了气膜阻尼结构的等效刚度系数和等效阻尼系数，并分析了气膜阻尼关键结构参数对抑振效果的影响。

国内外针对气膜阻尼的阻尼特性开展了大量研究，但对气膜阻尼的机理研究不够充分，尤其是基于机理建立的气膜阻尼理论模型研究不足。基于国内外现阶段研究成果，将气膜内气体的流动分别等效为牛顿流体的流动和泊肃叶流体的流动，建立了带气膜阻尼悬臂平板的振动模型，并推导出气膜阻尼系统的阻尼比方程。通过气膜阻尼能量耗散机理研究气膜阻尼结构参数对平板振动特性的影响，为航空发动机风扇叶片气膜阻尼结构设计提供理论依据和技术支撑。

2 带气膜阻尼的平板模型

航空发动机风扇叶片薄而长，对其进行振动特性分析时，可将风扇叶片等效为一端固支一端自由的悬臂梁或具有悬臂粱相似振动模态的薄板。带气膜阻尼的悬臂平板模型，如图1 所示。其结构包括平板、吸振薄板以及平板和吸振薄板之间的气膜。图中：2L 和2d—平板的长度和宽度；H—平板的厚度；2l 和h—气膜的长度和厚度，宽度与平板宽度相同，平板的厚度H 和气膜的厚度h 都远小于相应的长度和宽度，图中单位均为mm。计算时，假设悬臂平板左端固支，右端自由。

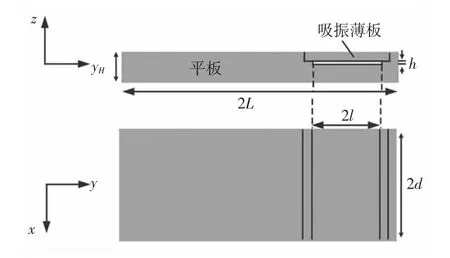
图1 带气膜阻尼的平板模型Fig.1 Schematic Diagram of the AFD Structure

3 气膜阻尼运动模型

带气膜阻尼平板模型含有多种振动能量耗散机制，如图1所示。（1）当叶片受气动力激励时，吸振薄板随平板振动，挤压气膜产生振动，以动能的形式耗散平板振动能量；（2）气膜内流体流动，当流体受挤压流经气膜壁面时，粘性剪切力消耗叶片振动能量；（3）气膜内外流体的流动，当带气膜阻尼平板振动时，由于气膜内外的压力差导致流体吸进或排出气膜，通过做功的形式耗散振动能量。因此，建立外激励所导致的气膜运动模型是建立气膜阻尼力学模型的前提。

3.1 气膜内流体的相对位移

假设图1 模型中气膜开口处的压力为常值，气膜内外没有能量交换，因此在气膜内选取流体运动的控制体[11]，如图2 所示。图1 中平板受激振力作用产生振动，假设n 和m 分别为吸振薄板的振动模态数，气膜由于吸振薄板振动引起的相对位移如式（1）所示：

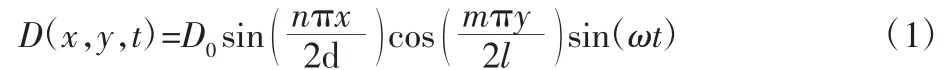
式中：D0—吸振薄板最大相对位移，单位为mm；

ω—吸振薄板振动频率，单位为Hz；

t—时间，单位为s；

（x，y）—气膜中流体任意点的位置。

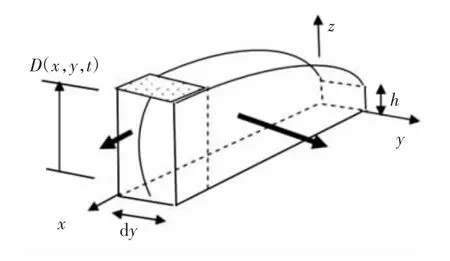
图2 气膜内流体的控制体Fig.2 Control Volume of the Fluid in the Air Film

3.2 气膜内流体的体积流量

由于气膜厚度远小于气膜长度和宽度，因此图2 中，假设x方向和y 方向为流体流动的方向，z 方向流动相对x 方向和y 方向忽略不计，因此进入控制体的流体体积流量为：

假设气膜内流体运动满足连续方程，由式（1）和式（2）可得x方向流体体积流量方程：

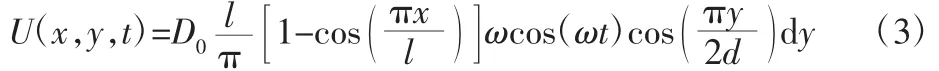
3.3 气膜内流体的运动速度分布

假设气膜内的流体具有牛顿流体的运动特性，流体运动的N-S 方程为：

式中：κ=-jρ0ω/μ—气膜内流体的复粘性系数。

在厚度方向上对式（7）进行积分可得穿过该截面的流体运动速度：

假设沿着x 轴方向运动的流体具有泊肃叶流动特性，因此z轴方向上流体的速度呈抛物线型分布：

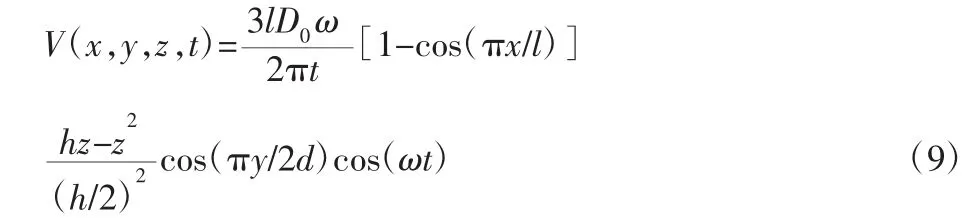
3.4 气膜内流体的压强分布

对于牛顿流体，假设压强p 沿气膜厚度方向（-h/2＜z＜h/2）是一致的。由方程（5）和式（6）可得密度、压力和相对位移之间的关系：

假设气膜内的流体为可压缩粘性流体，为使方程封闭，假设流体处于绝热状态，引入状态方程并用K 来表示复粘性系数κ和气膜厚度h 的关系[3]：

则流体的压强分布方程为：

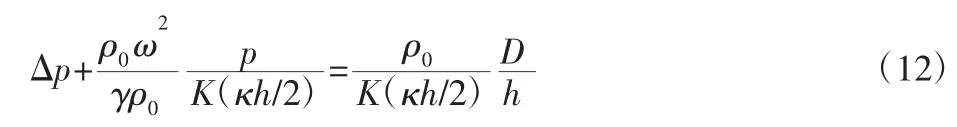
式中：γ—流体比热容。

假设图2 中y 方向流体位移一致且忽略边界处压力的变化，由式（10）和式（12）可得牛顿流体x 方向的压力分布：

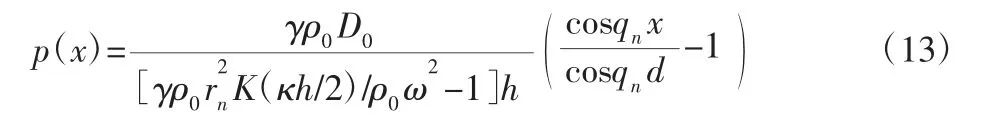
式中：rn—cos（rl）cosh（rl）=1 的n阶正根；qn—x 方向上的波数，由式（14）给出qn的定义[12-13]：

对于泊肃叶流体，假设气膜是一个复杂的弹簧，实部主要来自于可压缩性，虚部主要来自于粘性[12]，可以得到泊肃叶流体x方向的压力分布。

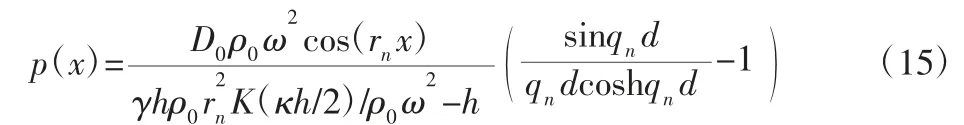
3.5 气膜阻尼平板内部能量耗散

设C 是气膜内部的每个振动周期的能量耗散：

对于牛顿流体，流体中粘性剪切力为主要的能量耗散方式，将式（8）带入式（16）得气膜阻尼内部能量耗散方程：

对于泊肃叶流体，将式（9）带入式（16）得到气膜阻尼内部的能量耗散方程[13]：

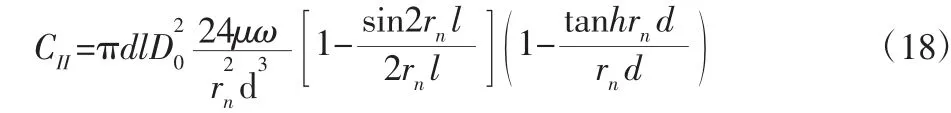
两种流体模型得到的能量耗散比值为：

为方便计算，引入阻尼比F（ω）：

4 带气膜阻尼平板的振动特性

大量研究表明：当吸振薄板与平板固有频率接近时，抑振效果明显[14]，因此这里在计算时，假设吸振薄板与平板固有频率相同。

4.1 不同流体模型的影响

气膜内流体分别采用牛顿流体和泊肃叶流体的计算结果，如图3 所示。由式（19）可得泊肃叶流体和牛顿流体计算得到的能量耗散的比值，如表1 所示。由图3 和表1 可知，无论采用哪种流体，在相同平板振动频率下（f＞300Hz），阻尼比随气膜厚度的增加而减少并最终趋于稳定。与牛顿流体相比，泊肃叶流体在计算振动能量耗散时，不仅考虑流体与板之间粘性剪切力引起的能量耗散，而且考虑了流体内部相互作用引起的能量耗散，因此在相同平板振动频率和相同气膜厚度的条件下，由泊肃叶流体流体计算得到的阻尼比要大于由牛顿流体得到的阻尼比。

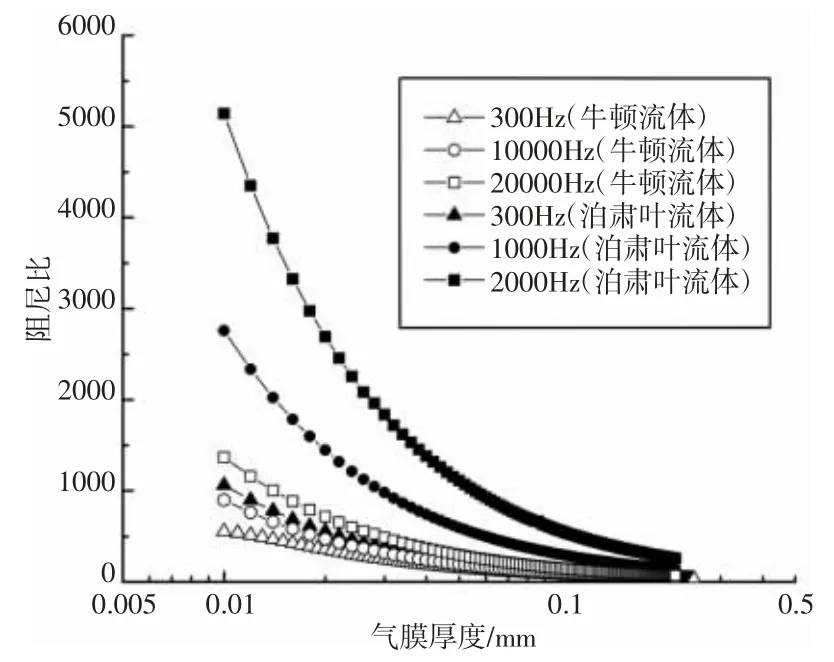
图3 基于不同流体模型的计算结果对比Fig.3 Comparisons of Results Based on Different Fluid Models

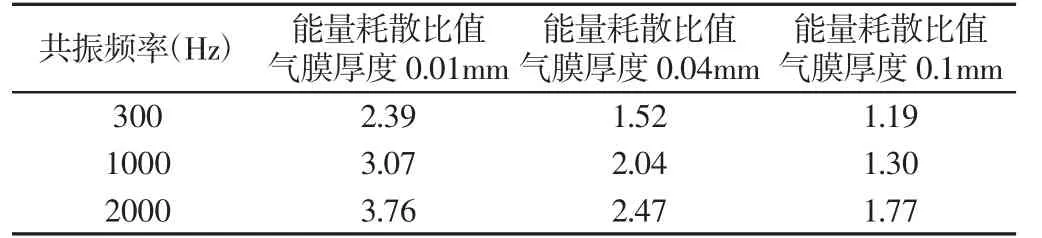
表1 两种模型的能量耗散对比Tab.1 Energy Dissipation Comparison of Two Models

4.2 气膜厚度的影响

不同平板振动频率（f＜300Hz），计算得到气膜阻尼的阻尼比随气膜厚度h 的变化曲线，如图3 所示。

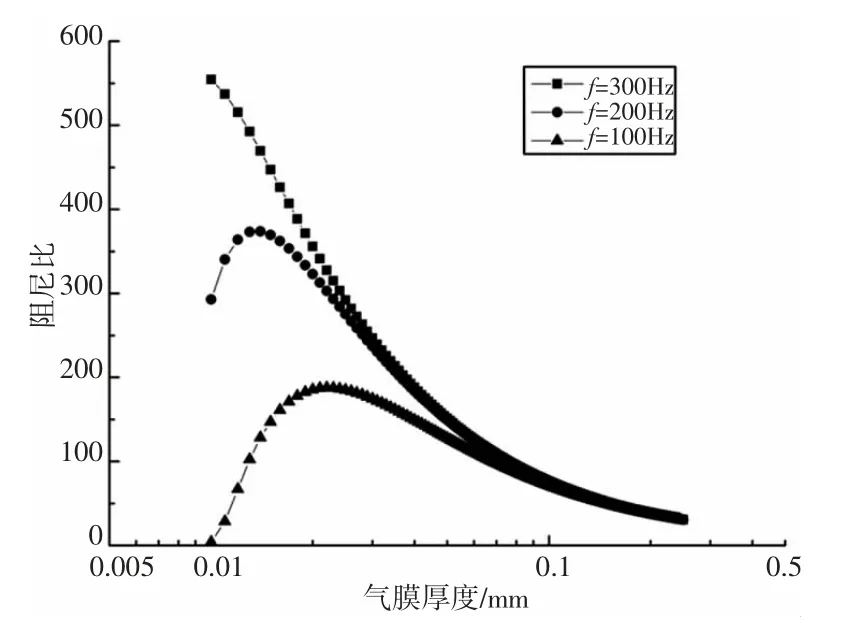
图4 不同频率下气膜厚度对阻尼比的影响Fig.4 Effect of Air Film Thickness on Damping Ratio at Different Frequencies

由图4 可知：平板的振动频率比较高时，气膜阻尼的阻尼比随气膜厚度的增加而降低并趋于稳定；平板的振动频率比较低时，气膜阻尼的阻尼比随气膜厚度的增大先增大后减小，之后趋于稳定。在相同气膜厚度条件下，平板振动频率越大，气膜阻尼的阻尼比也越大，气膜阻尼抑振效果越明显。

此外，当平板振动频率较低时，气膜阻尼存在最优厚度，这主要是在低频振动情况下，流体附面层厚度的影响不能忽略[8]。附面层厚度与平板振动频率的关系如下式（21）：

由式（21），平板振动频率越小，附面层厚度越大。当气膜厚度小于附面层厚度时，随气膜厚度的增加，粘性剪切力做功区域增加，振动能量耗散增加，阻尼比增加；当气膜厚度大于附面层厚度时，随气膜厚度的增加，流体流动时克服粘性剪切力产生的流动损失和能耗损失减小，导致阻尼比下降。

为进一步分析气膜厚度对阻尼比的影响，假设气膜内的空气为常温20℃，且气膜厚度大于流体附面层厚度[15]，求得平板一阶振动响应，如图5 所示。

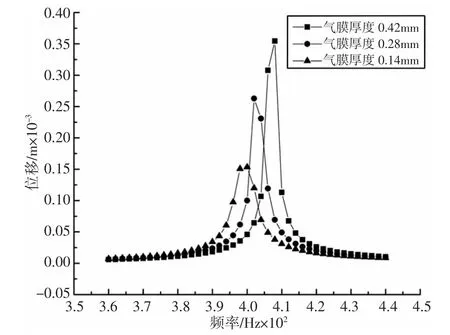
图5 厚度对气膜阻尼抑振效果的影响Fig.5 Effect of Film Thickness on Vibration Suppression Effect

由图5 可知：当气膜厚度大于附面层厚度时，不同气膜厚度计算得到的平板振动响应不同。随着气膜厚度的增加，平板振动位移增大，且最大位移发生的频率向频率增加的方向移动，这与文献[8-9]计算结果趋势一致。

由图4、图5 计算结果，气膜具有最优厚度，在设计航空发动机叶片气膜阻尼结构时，应综合考虑附面层厚度和振动频率，以得到最好的抑振效果。

4.3 气膜长度的影响

改变图1 气膜结构长度，计算得到平板振动响应，如图6 所示。

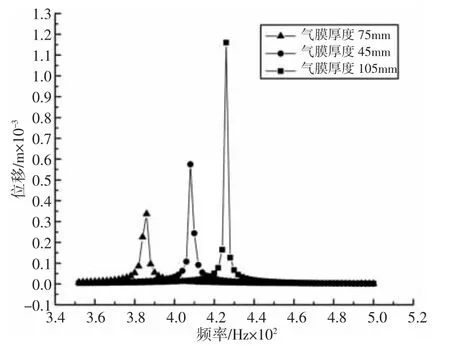
图6 长度对气膜阻尼抑振效果的影响Fig.6 Effect of Length on Vibration Suppression Effect

由图6 可知：当气膜长度为75mm 时，抑振效果最为明显，其他情况下平板振动幅度均有所增加。因此气膜阻尼具有最优长度，超过或低于该长度将降低其抑振效果。

4.4 气膜长度厚度比的影响

气膜的结构尺寸参数是影响气膜阻尼抑振效果的关键因素[9]，不同振动频率下气膜的长度厚度比与阻尼比的变化曲线，如图7所示。由图7 可知：不同振动频率下，阻尼比都随着长度厚度比的增加而增加。振动频率越大，阻尼比的增幅就越大。

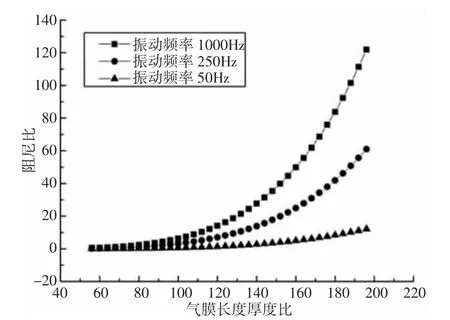
图7 气膜长度厚度比与能量耗散的关系Fig.7 Effect of Film Length-Thickness Ratio on Dimensionless Damping

4.5 安装位置的影响

保持气膜和吸振薄板沿平板厚度方向位置不变，改变其距自由端的距离，气膜阻尼在平板中不同安装位置，如图8 所示。

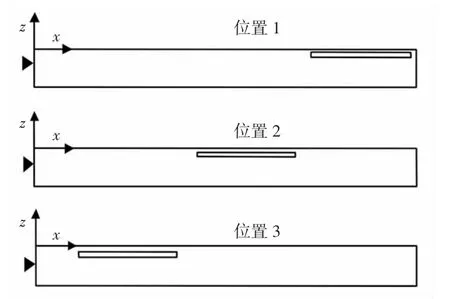
图8 气膜安装位置示意图Fig.8 Schematic Diagram of the Installation of AFD

不同安装位置计算得到的平板的振动响应与振动频率的关系，如图9 所示。

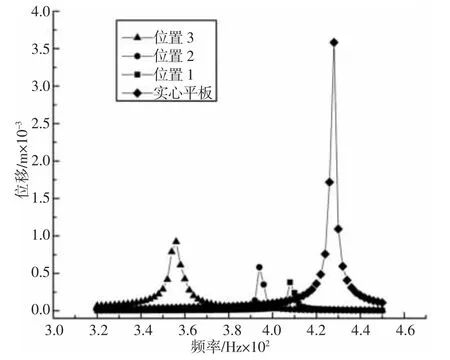
图9 安装位置对气膜抑振效果的影响Fig.9 Effect of Installation Position on Vibration Suppression

由图9 可知，气膜阻尼的安装位置不仅影响其抑振效果，也改变了平板的固有振动特性。平板的振动最大位移出现在自由端，气膜阻尼安装在该位置抑振效果也最为明显。由表2 可知：与实心平板相比，随着安装位置向固支端移动，平板的共振频率也向前移动。

表2 共振频率对比Tab.2 Comparison of Resonance Frequency

5 结论

将气膜内气体的流动分别等效为牛顿流体的流动和泊肃叶流体的流动，建立了带振动能量耗散机制的气膜阻尼理论模型。通过对带气膜阻尼悬臂平板的振动特性研究，确定了不同流动模型对计算结果的影响，以及在设计风扇叶片气膜阻尼时应关注的影响因素。泊肃叶流体能考虑更多的振动能量耗散机制，计算得到的阻尼比大于由牛顿流体得到的阻尼比；当平板振动频率比较低且流体附面层厚度的影响不能忽略时，气膜阻尼存在最优厚度；气膜的厚度、长度等几何尺寸对气膜阻尼的抑振效果有较大影响，在设计时应予考虑；气膜阻尼结构的安装位置不仅影响平板的抑振效果，而且改变了平板的共振频率。