基于固定方差展开的提升机主轴装置可靠性优化设计

任冯斌，曹 爽，卢 昊，2

（1.中国矿业大学机电工程学院，江苏 徐州 221116；2.中国矿业大学江苏省矿山机电装备高校重点实验室，江苏 徐州 221116）

1 引言

提升机主轴装置是提升机中重要的机械装备，其安全可靠是保证矿井高效稳定提升的重要保证，是提高煤炭产量与经济效益的重要前提。由于结构参数和载荷参数等具有不确定性，为保证提升机主轴装置满足预期的可靠性指标，就必须充分考虑不确定性的影响，在设计阶段进行准确的概率分析，从而满足提升机主轴装置初始可靠度的要求[1]。现阶段，可靠性理论已有了一定的发展，如在可靠性算法和可靠性优化理论等方面获得了较为广泛的研究[2—9]。

针对提升机主轴装置开展基于可靠性的结构优化设计，可以在获得各参数最优组合的条件下，满足该类装备零部件的可靠度要求，从而使得整体装备具备抵抗不确定性的能力。在保证结构可靠度求解精度的前提下，通过将结构的可靠性指标作为优化设计模型的约束之一，即可在保证结构得到最优参数的同时，保证结构满足期望的可靠度要求[10-11]。依据提升机主轴装置的实际工况，建立了其强度失效的极限状态函数，并将其通过Taylor 级数展开到二阶，基于固定方差展开方法获得了极限状态函数的前三阶矩。根据可靠性理论和基于矩的鞍点逼近方法计算得到了提升机主轴装置的失效概率。将所求得的结构可靠度作为约束，建立了提升机主轴装置的可靠性优化设计模型。数值算例表明，方法可有效地开展提升机主轴装置的可靠性及可靠性优化设计。

2 基于固定方差展开的高阶统计矩计算

根据可靠性分析的基础理论，首先建立提升机主轴装置的极限状态函数。

一般地，极限状态函数可表示为如下形式：

若使用固定方差展开，上述可靠性功能函数可以写成：

式（3）中的方差展开项可以由下式计算：

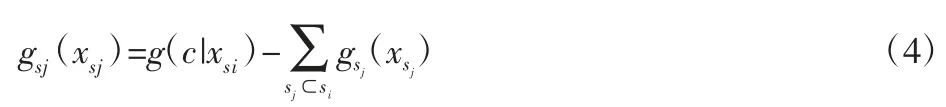
式中：c=［c1，…，cN］—固定点；

g（c|xsi）—在固定点c 代入g（x）所得的计算值。

具体计算过程可参见文献[12]。

根据式（4），功能函数g（x）的均值可以表达为所有展开项的代数和，即：

类似地，功能函数的方差可以表示为所有展开项方差的代数和，即：

3 基于鞍点逼近的可靠性分析

基于矩的鞍点逼近是在获取状态函数前几阶矩的基础上，通过拟合高阶矩得到状态函数的逼近分布函数[13-14]。基于矩的鞍点逼近方法可以表达为：

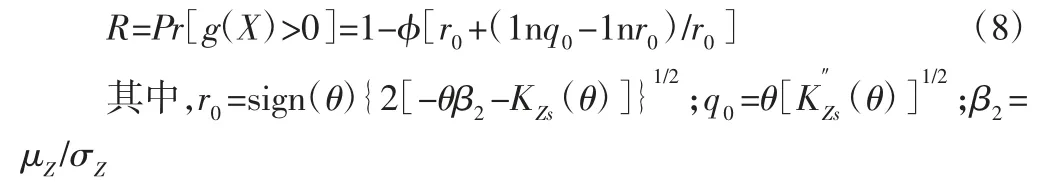
其中，sign 函数有sign（y）=1，-1，or 0（y＞0，y＜0 or y=0）。与传统的鞍点逼近方法相比，式（8）所表述的鞍点逼近方法使用了逼近的累积量母函数，从而避免了随机变量累积量母函数不存在的情况。

所采用的逼近累积量母函数表达为：

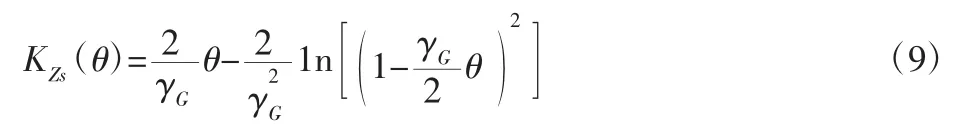
其二阶偏导数表达式为：

当求得结构功能函数的前三阶统计矩后，便可代入到式（8）中进行结构可靠度的计算。

4 可靠性优化设计

在结构可靠性分析的基础上，基于传统的优化设计模型，建立了提升机主轴装置的可靠性优化设计模型如下[15]：

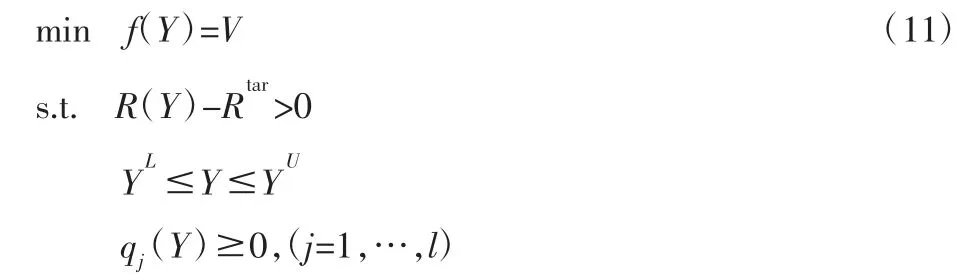
式中：Y—设计变量向量；

V—提升机主轴装置的体积；

R（Y）—提升机主轴装置的强度可靠性；

Rtar—可靠性约束的期望可靠度；

YL和YU—设计变量向量的下限和上限；

qj（Y）—变量需满足的非线性约束。

5 数值算例

提升机主轴装置是提升机中最为关键的机械部件，针对提升机主轴装置的强度可靠性及结构优化问题开展研究。提升机主轴装置的三维模型，如图1 所示。随机变量的统计特性，如表1 所示。

在建立提升机主轴装置仿真模型的基础上，开展了提升机主轴装置随机响应的仿真分析，其应力云图，如图2 所示。由于大型矿井提升机主轴装置的载荷条件复杂、结构参数较多，导致随机仿真分析涉及的参数众多，因此，采用基于拉丁超立方抽样技术进行随机变量的试验设计，结合有限元分析方法开展了提升机主轴装置应力响应的随机仿真分析，从而获得最危险位置结构应力的随机响应。

图1 提升机主轴装置三维结构图Fig.1 Three Dimensional Structure Diagram of Hoist Main Shaft Device

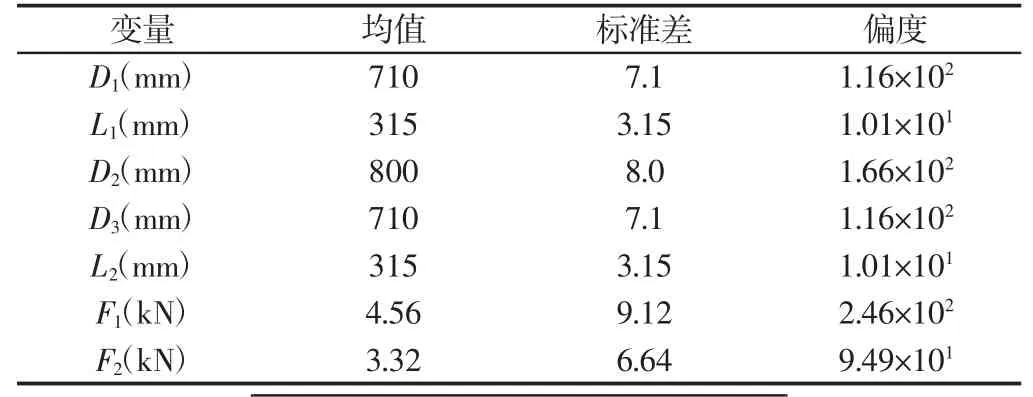
表1 提升机主轴装置随机变量的统计特性Tab.1 Statistical Characteristics of Random Variables of Hoist Main-Shaft Device

图2 提升机主轴装置应力云图Fig.2 Stress Nephogram of Hoist Main Shaft Device

由Kriging 相关理论，将随机变量样本点矩阵及应力响应样本设定为已知信息、回归模型选取为固定值、采用高斯相关方程，建立Kriging 最优模型：

根据广义应力—强度干涉理论，提升机主轴装置强度失效的极限状态方程和可靠性模型可分别表示如下：

应用这里提出的基于固定方差展开的鞍点逼近方法得到提升机主轴装置的失效概率为：

Pf=0.01197

根据这里所提出的可靠性优化设计模型，设期望可靠度为0.99，设计变量为：

Y=［D1，L1，D2，D3，L2］T=［710，315，800，710，315］，通过优化得到优化后的结构参数为Y*=［D1，L1，D2，D3，L2］T=［639.58，347.11，820.92，767.78，324.67］。优化后的提升机主轴装置能够在满足目标可靠度的同时，实现体积的最小化。通过可靠性优化设计能够有效改善提升机主轴装置的现有结构。

6 结论

提出了一种基于固定方差展开的提升机主轴装置可靠性优化设计方法。

（1）采用二阶Taylor 级数展开可靠性功能函数，结合固定方差展开分析获得了功能函数的前三阶统计矩；

（2）根据基于矩的鞍点逼近方法，得到了结构的可靠性指标和失效概率；然后，建立了基于可靠度约束的可靠性优化设计模型；

（3）将所提出的可靠性方法应用于提升机主轴装置的可靠性优化设计中，实现了提升机主轴装置结构参数的优化设计。