带机械臂四旋翼飞行器的控制方法研究

周祖鹏，甘良棋，张晓东

（桂林电子科技大学机电工程学院，广西 桂林 541004）

1 引言

四旋翼无人机是一种结构简单，具有垂直起降和着陆能力的空中机器人。在军事领域、民用领域、商业领域逐渐体现出它特有的优势[1]，例如可用于无人机侦查、航拍、搜寻营救及植保等[2-3]。近些年来，四旋翼无人机在军事研究、无人机爱好者、民用、商业用途等方面越来越受到关注。随着卫星和无人机技术的快速发展，MEMS 技术已经广泛应用于国防，军用和民用产品，工艺和信息技术的各个方面。飞机的小型化导致无人驾驶的广泛使用的急剧增加，这已经成为许多国家研究的一个热门主题。无人机是指在没有飞行员的情况下运动的空中机器，它是利用空气动力驱动来克服自身的重量，可以远程控制或自主飞行，并且可以承受一定的载荷。无人机拥有质量轻，实地勘察，可以做到24h 侦查、监视，目标获取、拦截和战斗现场评估，甚至可以直接攻击重要目标等功能。鉴于无人机广泛的使用和在现代战争中出色的表现，国际社会掀起了一股新的研究浪潮，许多国家越来越重视无人机在军事方面的应用。因为固定翼无人机的控制系统很复杂，并且早期时候不能实现自主飞行控制，同时起飞与降落都需要跑道等，导致固定翼无人机的发展是比较缓慢的。在可以垂直起飞与降落的无人机中，四旋翼飞行器具有独特的结构[4]，同时也拥有起飞与降落、甚至携带很方便的特点，这是固定翼飞行器所不能堪比的。与传统的固定翼无人机相比，四旋翼无人机的结构更加简单，其四个螺旋桨对称布置，通过改变四个螺旋桨的转速，从而使四旋翼无人机达到理想的姿态与位置，实现了各种飞行控制[5-6]。这些优势使得四旋翼无人机在军事和民用应用具有广阔的前景，特别是在低空环境下作业：如室内、野外丛林和繁华都市等侦察、监控和其他特殊任务。文献[7]，提出改进的模糊PID 姿态控制，具有良好的鲁棒性和控制精度。文献[8]，对比经典PD 控制、智能模糊控制、非线性反步法和滑模变结构控制，提出并设计四旋翼姿态和高度控制器，对比仿真结果表明滑膜变结构控制具有更好的动态跟踪特征。文献[9]，提出了一种自适应滑膜控制方法，既提高系统的鲁棒性，又补偿了由模型误差及外界扰动带来的误差。文献[10]，采用双闭环PID 控制飞行器的姿态。文献[11]，采用近似线性化方法得到解耦后的线性化模型，利用该模型分别采用PID、极点配置和线性二次模型最优法三种方法设计了飞行器高度控制算法。文献[12]，提出了一种非线性鲁棒以及在线参数估计算法的控制器，且实验表明该控制器消除了颤振现象。文献[13]，提出了位置式的PID 控制算法比较准确地控制四旋翼飞行器的姿态。文献[14]，设计了一种新的几乎全局稳定非线性姿态控制器，由一个线性PID 控制部分和一个惯性力矩补偿部分组成。文献[15]，对比分析模糊PID 和传统PID 应用在四旋翼无人机的控制，得出模糊PID控制算法更具有优良的动态性和鲁棒性。文献[16]，采用积分分离PID 控制算法对四旋翼飞行器的姿态和位置做闭环控制。文献[17]，验证得出模糊自整定PID 控制算法优于传统PID 控制算法。以上方法可以总结为经典PID 控制，但是其存在抗干扰能力差，鲁棒性弱等缺点；线性二次型调节器具有一定的延迟不足；反步控制算法与神经网络控制法需要有大量的训练数据来进行计算，对微处理控制器有较高的要求。从实际问题出发，结合四旋翼飞行器自身特点，携带机械臂四旋翼无人机可以完成许多具有危险性和困难性的任务，比如江面投放救援器材，灾情的迅速勘探和救灾物资的投放等，所以对于研究携带机械手四旋翼无人机的实际应用有一定的影响。

2 四旋翼无人机建模

2.1 四旋翼无人机坐标系表示

四旋翼无人机是一种欠驱动系统的无人机，四个螺旋桨对称布置，如图1 所示。在四旋翼无人机中，对称布置四个螺旋桨，由他们来提供动力，控制四旋翼无人机的姿态和位置，如图1 所示。通过同时增加或减小四个螺旋桨的转速来控制四旋翼无人机的上升或下降；通过增加或减小前面两个螺旋桨的转速来获得四旋翼无人机的俯仰运动；通过增加或减小左边两个螺旋桨的转速来获得四旋翼无人机的翻滚运动；通过增加或减小两个不相邻的两个螺旋桨的转速来获得四旋翼无人机的偏航运动[18]，具体如下表1 所示，四旋翼基本运动对应的电机需求。

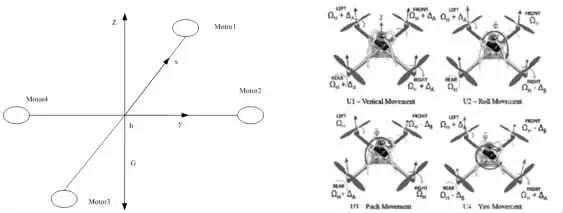
图1 四旋翼无人机坐标系Fig.1 Quadrotor Coordinate System

图中：x，y，z—欧拉角沿着x 轴转动的是翻滚角（Roll），沿着y 轴转动的是俯仰角（Pitch），沿着z 轴转动的是偏航角（Yaw），且转动的角度分别用φ，θ，ψ 表示；定义四个控制量分别是垂直移动控制量U1，翻滚控制量U2，俯仰控制量U3，偏航控制量U4；Ωi（i=1，2，3，4）—四旋翼无人机的四个螺旋桨的转速；“+”，“-”—螺旋桨转速增加和减小。

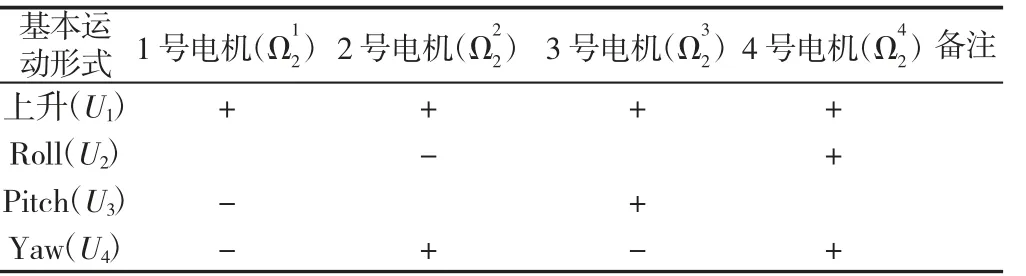
表1 四旋翼无人机基本运动对应的电机需求Tab.1 Motor Requirements for Basic Motion of a Quadrotor

2.2 欧拉方程

物体只有位置变换（平移变换）和朝向变换（旋转变换）发生改变，而形状不便，得到的变化称为刚性变换。

转换方程：式中r 表示质心位置，m 表示刚体质量，根据牛顿第二定律，可以得到：

式中：ξE—惯性系下的速度矢量；υB—机体系下的速度矢量；HΘ—机体系下的速度矢量转换到惯性系速度矢量的转化矩阵。基于牛顿-欧拉方程的四旋翼无人机的动力学方程[19]如下：

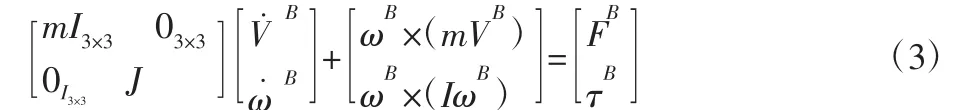
式中：m—四旋翼无人机的质量；J—转动惯量；I3×3—单位阵；ωB和VB—机体系下四旋翼无人机的角速度和四旋翼无人机的线速度；FB和τB—四旋翼无人机的受力和力矩。

2.3 四旋翼无人机的动态建模

下面的假设是为了简化四旋翼无人机的动力学模型：

（1）四旋翼无人机的质心与机体坐标系的原点重合；

（2）四旋翼无人机的惯性轴与机体坐标系轴一致。

根据上面的假设，关于机体坐标系下的加速度可以表示如下：

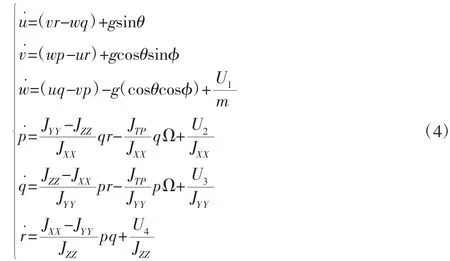
在混合坐标系下得到四旋翼无人机的动态建模方程[20-24]如下：

我国正在推行的最严格水资源管理制度，引起了国内外有关领域和各界广泛关注。作为中国水资源保护、管理以及国际交流与合作的积极推动者，全球水伙伴中国委员会于2012年4月20日在北京举办中国水资源管理制度建设高级圆桌会议。水利部部长陈雷出席会议并致辞，十一届全国人大财经委员会副主任委员、全球水伙伴中国委员会主席汪恕诚主持会议，国家发展改革委副主任杜鹰出席会议并致辞，国务院南水北调工程建设委员会办公室副主任于幼军出席会议。来自不同地区、部门、区域、行业及各相关组织的代表和专家汇聚一堂，共同探讨加强中国水资源管理制度建设的有关问题。

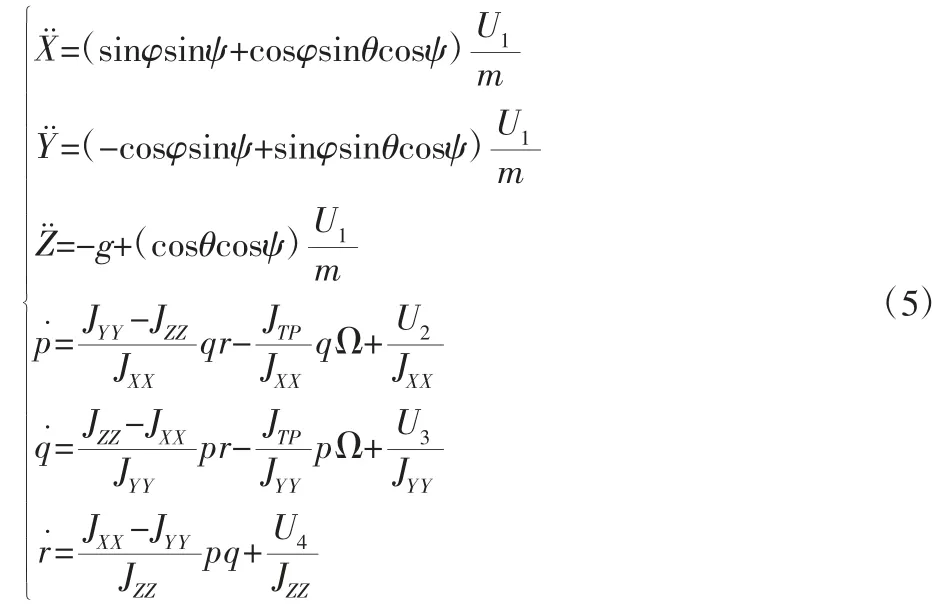
式中：m—四旋翼无人机的质量；

g—重力加速度；

JTP—螺旋桨的转动惯量。

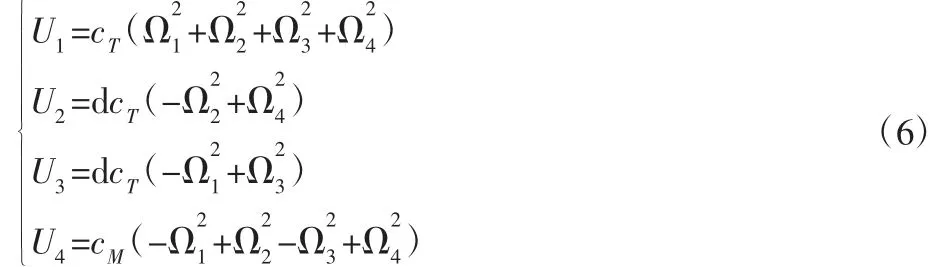
式中：cT—螺旋桨的拉力系数；

cM—扭矩系数；

d—无刷电机的中心轴到四旋翼无人机机体轴的距离。

3 控制模型设计

3.1 控制器结构

通过拉普拉斯变换得到的传统PID 结构表示如下：

式中：e（s）—输入与输出之间的误差；u—控制的输入信号；Kp、Ki、Kd—比例系数，积分常数，微分常数。

由四旋翼无人机的数学模型可知：四旋翼无人有四输入六输出，强耦合，非线性，是典型的欠驱动系统。采用PID 控制器对四旋翼无人机飞行进行控制时，首先需要解决数学模型的解耦线性化处理，实现单通道的控制。在四旋翼无人机的控制系统中姿态控制是核心控制[25]，它与位置控制存在着半耦合关系，并且姿态控制的效果好坏直接影响整个四旋翼无人机系统的飞行质量。本论文把四旋翼无人机的控制系统简化成姿态通道系统和高度通道系统两部分进行控制。

高度通道、翻滚通道、俯仰通道和偏航通道分别使用串联PID 进行独立控制。四个独立的串联比例积分控制器分别用于控制四旋翼飞行器的四个基本运动[26]。这种控制器的优点是，可以尽量消除系统中间产生的误差。串联PID 控制器的一般结构，内环PID 控制姿态角速度，外环PD 控制姿态角度。

调整四旋翼螺旋桨的转速从而实现对四旋翼无人机的姿态与位置的控制。通过式（6）可以得到Ω2与U 之间的转换关系如下所示[27]：

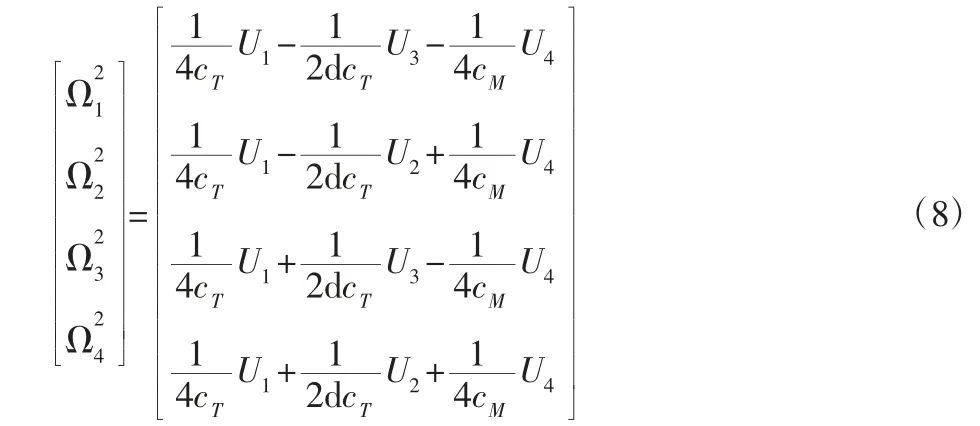
3.2 Simulink 设计

基于matlab/Simulink 设计的仿真结构包括四旋翼无人机的动态模型，控制器模型，螺旋桨模型与可视化模型。我们可以简化四旋翼无人机动态模型的方程如下：

根据PID 系统结构图，搭建模型并仿真，四旋翼建模框图，如图2 所示。

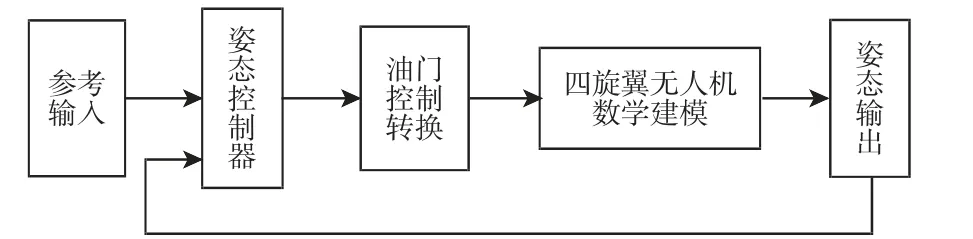
图2 四旋翼无人机仿真建模Fig.2 Simulation Modeling of the Quadrotor

仿真建模参数辨识结果，如表2 所示。

表2 四旋翼无人机参数辨识Tab.2 Parameter Identification of Quadrotor

在matlab/Simulink 中搭建如下模型：四旋翼无人机姿态角加速度，如图3 所示。四旋翼无人机姿态角及位置，如图4 所示。

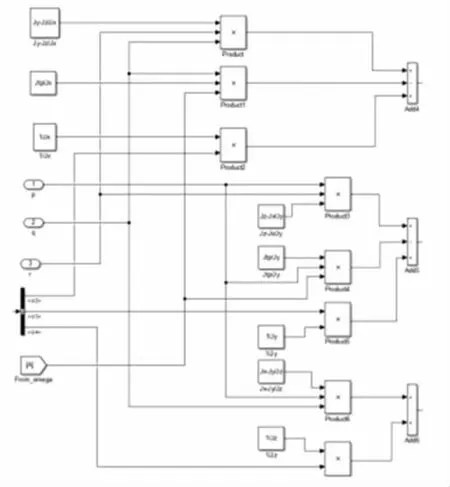
图3 四旋翼无人机姿态角加速度Fig.3 Attitude Angular Acceleration of the Quadrotor

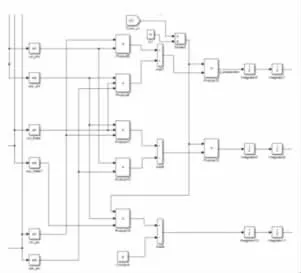
图4 四旋翼无人机姿态角及位置Fig.4 Attitude Angular and Position of the Quadrotor

3.3 仿真结果分析

从仿真结果，分别展示了翻滚、俯仰、偏航和高度信号的阶跃信号响应曲线。我们给定的初始φ=0.087266rad，θ=0.087266rad，ψ=0.087266rad。

每个通道设置了单独的PID 参数辨识，如表3 所示。

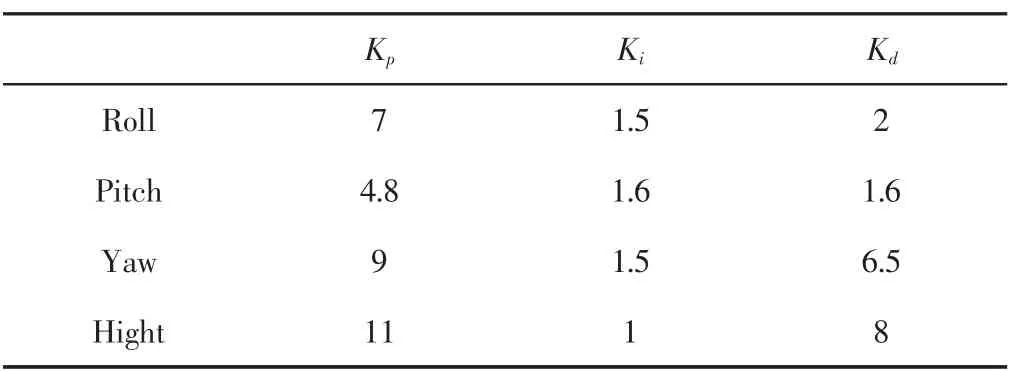
表3 姿态与位置各个通道PID 参数数值Tab.3 Position and Attitude of PID Parameters of Each Channel

如下图所示分别是翻滚角、俯仰角、偏航角的姿态响应曲线，实际输出姿态角与理想姿态角之间的误差曲线。图8 表示的是高度方向上阶跃响应曲线，实际输出与理想输出之间的误差曲线。对于姿态与位置各个通道实际的PID 参数辨识，如表3 所示。利用matlab/Simulink 模块进行了仿真实验，根据以上数据，四旋翼飞行器的仿真实验可以实现姿态与位置的控制要求。从下表可以看出，翻滚角和俯仰角的系统超调小，并且响应速度快；偏航角的控制器系统响应速度快；高度方向系统超调量为0，动态性能好设计效果较好。

仿真结果响应曲线如下：

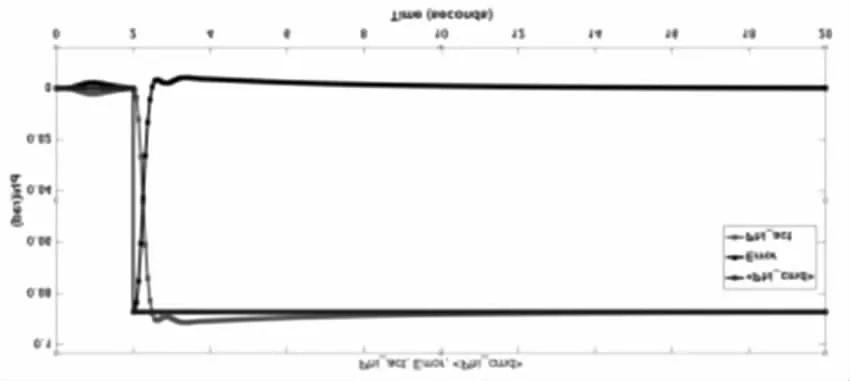
图5 翻滚角输出与误差响应Fig.5 Output of Rolling Angle and Error Response

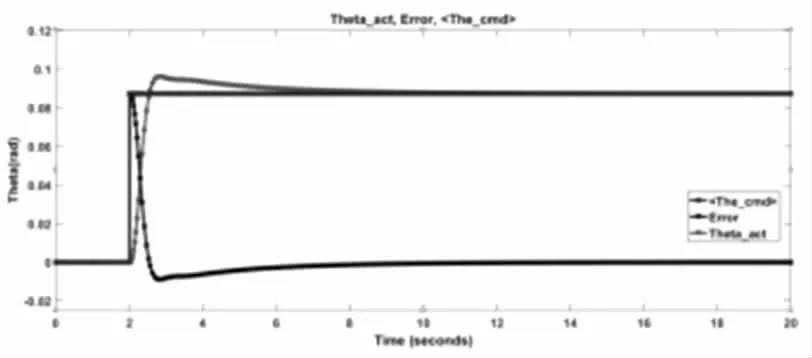
图6 俯仰角输出与误差响应Fig.6 Output of Pitch Angle and Error Response

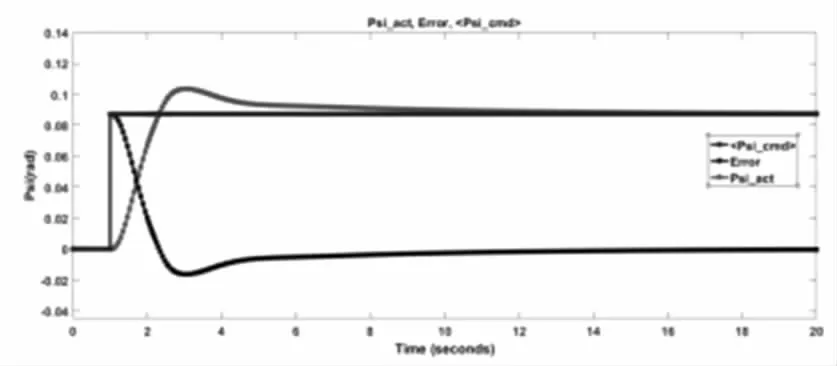
图7 偏航角输出与误差响应Fig.7 Output of Yaw and Error Response

图8 四旋翼无人机起降高度阶跃响应Fig.8 Height Step Response

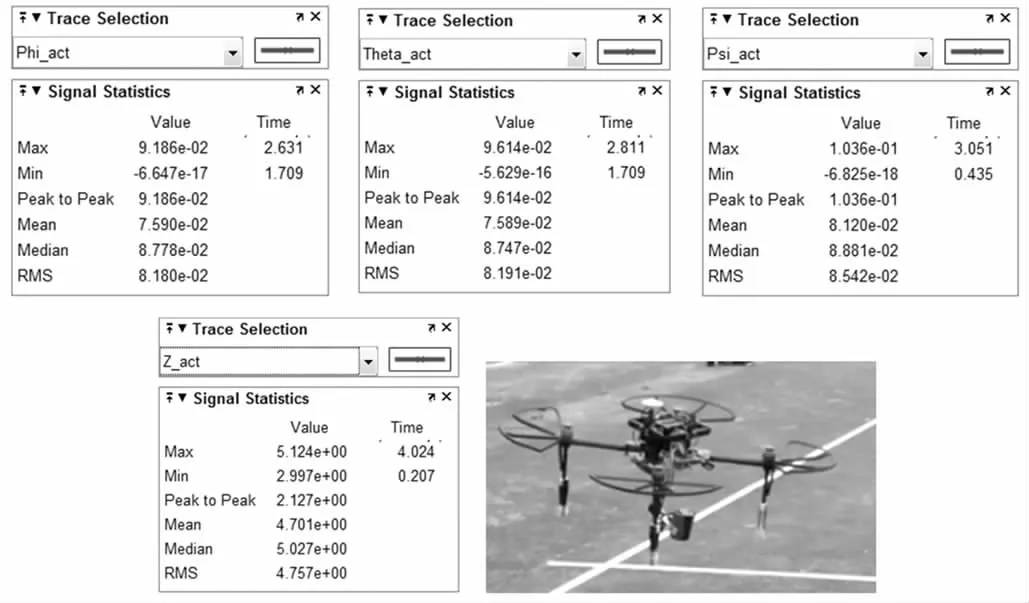
图10 带机械手的四旋翼无人机Fig.10 The Quadrotor with Mechanical Arm

4 结论

对四旋翼飞行器进行了动力学建模和运动学建模，并且建模的基础上分别设计了翻滚、俯仰、偏航和高度通道的PID 控制器，将四旋翼飞行器的控制系统分为姿态控制和位置控制，基于抗饱和串联PID 控制器对四旋翼飞行器进行了控制。结合图5 与图9 所示翻滚角的阶跃信号响应曲线，时间0.614s 后系统稳定；结合图6 与图9 所示俯仰角的阶跃信号响应曲线，时间为0.811秒后系统稳定；结合图7 与图9 表示偏航角的阶跃信号的响应曲线，时间为1.051s 后系统稳定；结合图8 与图9 反映的是四旋翼飞行器在高度方向上的阶跃响应曲线，时间为2.811s 后系统稳定。仿真显示了PID 控制器设计的有效性，能够实现四旋翼无人机的控制飞行。如图10 所示是试飞实验实拍图，在研究携带机械手四旋翼无人机的应用有一定的影响。