颗粒状腐蚀产物在水跨临界区域近壁面传质特性的模拟
2021-03-05侯天琦李鸿源
王 超,侯天琦,李鸿源,徐 鸿
(华北电力大学 能源动力与机械工程学院, 北京 102206)
超(超)临界发电技术可实现能源高效转换,在火电、下一代核电以及太阳能热发电中有广阔的发展前景。当温度和压力超过热力学临界点374.3 ℃、22.1 MPa时,工质水进入超临界态,称为超临界水(Supercritical Water,SCW)。
电站汽水系统中超临界区域受热面管内壁氧化主要由两部分组成,一部分是管壁金属在超临界水作用下形成的金属氧化内层,另一部分是由随工质迁徙的腐蚀颗粒沉积形成的沉积层。超临界区域管内形成的内外层氧化物在应力作用下会开裂、剥落。剥落物在随工质运动过程中可能会堆积在汽水系统中流速剧烈变化区域,严重时造成堵管、爆管等事故[1]。
由电站低温给水系统流动加速腐蚀(FAC)产生的腐蚀产物Fe离子随工质在汽水循环中迁徙[2-3],当Fe离子迁徙至工质超临界区域时,会快速(结晶时间为0.1~1 s)[4]脱水结晶[5]形成颗粒。因此,工质的跨临界区域是腐蚀颗粒沉积的起始位置,也是关键区域,揭示跨临界区域内腐蚀颗粒的传质规律对进一步控制超临界水工质氧化具有重要意义。
研究表明,超临界水中颗粒态腐蚀产物沉积速率的主导过程为湍流传质过程[6]。但是超临界水在临界点附近会发生剧烈的热物理性质变化,由于超临界水的温度和压力较高,难以直接观察其湍流流动,数值模拟是分析超临界水湍流流动最有效的方法,当前的研究多集中于采用数值模拟方法来研究跨临界流动和传热[7-9],而对跨临界湍流中颗粒向近壁面扩散规律的研究较少。
近年来,基于雷诺时均纳维-斯托克斯方程(Reynolds-Averaged Naviere Stokes,RANS)的湍流模型结合离散相模型(Discrete Particle Model,DPM)的颗粒运动数值模拟已经得到了广泛的研究[10]。鉴于RANS计算资源占用少的优势,利用Fluent软件开展基于RANS-DPM方法的腐蚀颗粒在跨临界区域内沉积行为模拟,研究跨临界湍流中颗粒近壁面扩散规律,为超临界机组通流结构优化设计和运行调整提供理论指导。
1 数学模型
采用RANS-DPM方法对颗粒运动进行求解前,首先需要选择合适的湍流模型,k-ω模型具有很好的湍流边界层适用性,其中SSTk-ω湍流模型考虑了剪切应力的传递效应。曲默丰等[11]基于文献传热实验数据验证了SSTk-ω湍流模型的准确性,因此笔者选用SSTk-ω湍流模型来描述连续相超临界水的流动。采用 Favre 平均法,流动计算中质量方程、动量方程和能量守恒方程分别如下:
(1)
(2)
(3)

选用离散相模型计算颗粒的运动,颗粒的体积分数应该小于10%,可以忽略颗粒与颗粒之间的相互作用,也不考虑颗粒体积分数对连续相的影响。因此,颗粒在流体中的运动仅考虑流体对颗粒的作用力,颗粒的运动方程为:
dup/dt=3μ(u-up)CDRep/4d2SCc+
g(ρp-ρ)/ρp+Fx
(4)
式中:S为颗粒与流体的密度比;μ为流体动力黏度,Pa·s;d为颗粒直径,m;Rep为颗粒雷诺数;CD为曳力系数;Cc为Cunningham滑移修正系数,Rep、CD和Cc的设定可参考文献[12];up为颗粒速度,m/s;ρp为颗粒的密度,kg/m3;Fx为Saffman升力、热泳力及布朗力的合力项,可参考文献[6]。
2 几何模型及参数设置
2.1 几何模型
选取典型直管进行模拟,管径取3.35 mm,将管入口定义为起点,沿管长方向为轴向,管入口到管出口的轴向距离为1 m。采用六面体网格进行网格划分,选择增强型壁面函数,第一个网格中心y+=1时,第一层网格距离壁面2.3 μm,对管道近壁面网格进行加密,网格划分如图1所示。研究中以壁面为起始点,将距离壁面y0=26.1y+(即厚度为60 μm)的区域定义为近壁面区域。

图1 网格划分Fig.1 Grid division
根据壁面函数的网格划分结果,轴向网格节点数为3 500,为轴向等分,整体采用多区域处理,截面网格是很明显的O型网格,计算适应性好,近壁面网格加密明显,满足了壁面函数对y+的要求。总网格数为310 000,总网格节点数为324 421,对划分的网格进行了网格质量检查,结果表明网格质量符合Fluent软件的要求。
2.2 参数设置
流体边界条件如表1所示,计算压力均为25 MPa。Fe的氧化物颗粒的主要成分为Fe3O4,颗粒密度ρp=5 180 kg/m3。

表1 计算参数
连续相采用压力和速度耦合的Simplec算法,在连续相收敛之后,对残差控制精度进行修改,除了能量项外所有变量的残差设为0.000 5。颗粒从直管入口面喷入,常温下颗粒的质量浓度为6.8 μg/L,颗粒的速度与流体的入口速度相同,不存在入口处的滑移速度。
2.3 模型验证
为了对模型计算的准确性进行验证,选择实验关系式式(5)[13-14]与实验关系式式(6)[15]进行对比。
(5)
(6)



图2 数值模拟结果与实验关系式计算结果的对比Fig.2 Comparison between numerical simulation and the resultscalculated by empirical relations
3 结果与分析
3.1 入口温度对近壁面颗粒质量浓度的影响
工况4下水的近壁面温度和速度分布分别见图3和图4。25 MPa时,伪临界温度为384.5 ℃。如图3所示,近壁面温度要明显高于主流水温度,假设每条温度曲线与伪临界温度线的交点到壁面的距离为超临界层厚度,轴向距离0.2 m位置开始近壁面温度就已经进入了超临界区域,但直到轴向距离0.4 m处,超临界层厚度均较小。轴向距离0.5 m位置出现最高近壁面温度,将此处对应的轴向位置定义为跨临界点,跨临界点具有近壁面区域边界(y0=26.1y+)恰好达到超临界态的特点。根据图4,跨临界点附近近壁面速度增幅较大,轴向距离0.5~0.7 m位置温度偏高是传热恶化的原因。

图3 工况4下近壁面温度分布Fig.3 Near-wall temperature distribution under condition 4

图4 工况4下近壁面速度分布Fig.4 Near-wall velocity distribution under condition 4
不同入口温度下近壁面颗粒质量浓度如图5所示。工况4(入口温度为310 ℃)中,颗粒质量浓度峰值对应的轴向位置与跨临界点的轴向位置相近,跨临界点附近近壁面速度增幅较大。因此,可假设近壁面完全超临界态与沉积速率峰值存在对应关系,在湍流作用下,跨临界点附近剧烈的密度变化加速了近壁面区域与主流水之间的质量交换,使得颗粒向近壁面的扩散量增加,超临界层厚度过小或过大都不会引起近壁面颗粒的聚集,而是趋向于均匀分散在整个管子横截面上。

图5 不同入口温度下近壁面颗粒质量浓度分布(qm=0.013 9 kg/s,q=0.14 MW/m3)Fig.5 Near-wall particle concentration distribution at differentinlet temperatures
工况6(入口温度330 ℃)和工况7(入口温度350 ℃)同样存在颗粒的质量浓度峰,与工况4(入口温度310 ℃)相比,入口温度的升高使得近壁面区域完全超临界态对应的轴向位置提前,峰的轴向位置的关系为:工况4>工况6>工况7。但由于水质量流量和加热功率相同,入口温度仅改变了近壁面完全进入超临界态的位置,因此对颗粒质量浓度的峰值几乎没有影响。
3.2 热流密度对近壁面颗粒质量浓度的影响
工况5下水的近壁面温度分布如图6所示,工况2和工况5下获得的近壁面颗粒质量浓度分布如图7所示。与图4中工况4的近壁面温度分布相比,工况5下最高近壁面温度提前至轴向距离0.3 m的位置,而且从轴向距离0.4 m起,近壁面区域开始完全进入超临界态。
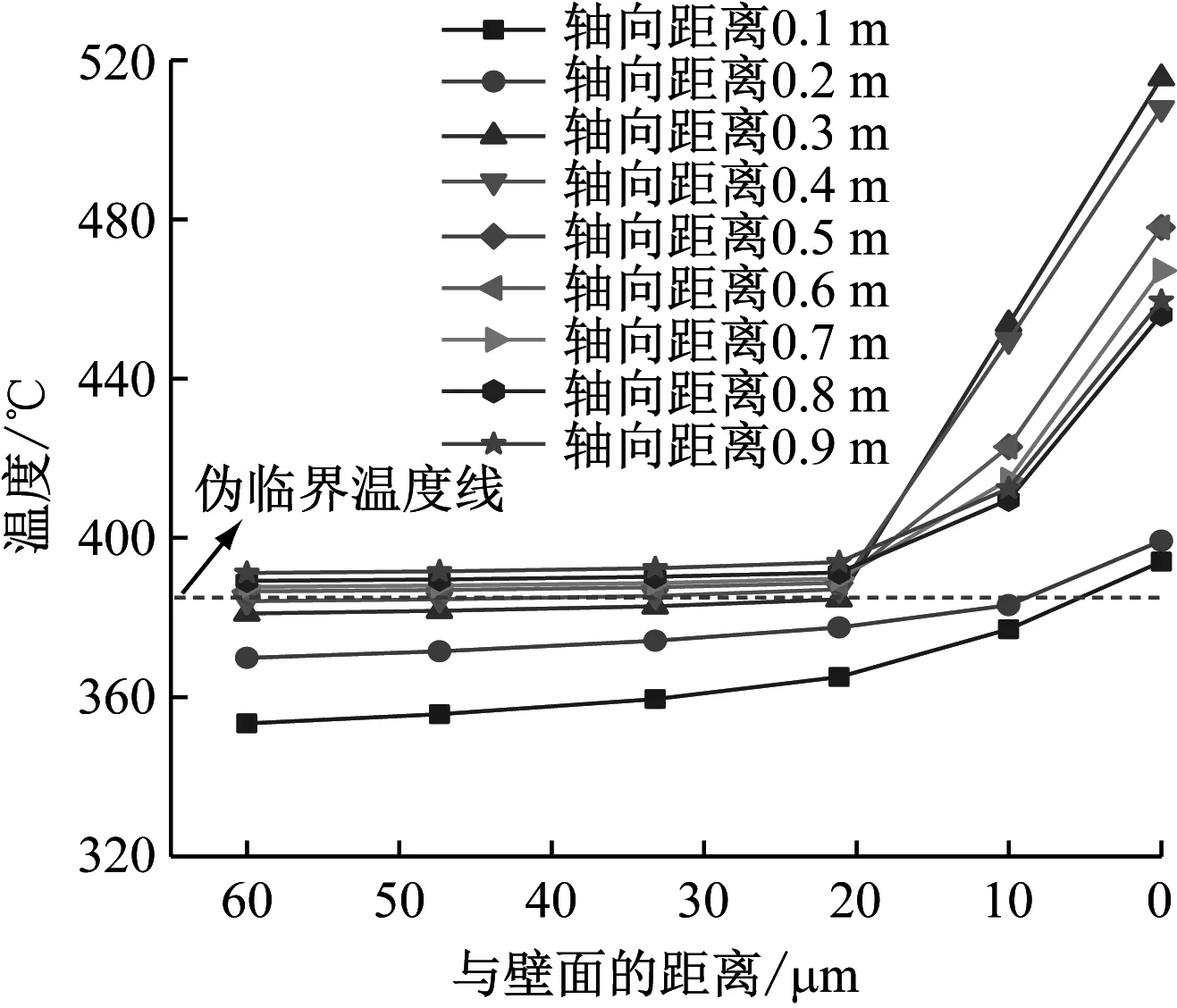
图6 工况5下近壁面温度分布Fig.6 Near-wall temperature distribution under condition 5
对比图6与图7,工况5下近壁面颗粒质量浓度峰值出现在轴向距离0.4 m位置,与所提出的跨临界点与近壁面颗粒质量浓度峰值存在对应关系的假设相符合。对比不同热流密度下近壁面颗粒质量浓度峰值可知,增大加热功率降低了近壁面颗粒质量浓度,可能是因为高加热功率下,轴向距离0.4 m位置的流体密度下降较快,使得近壁面速度梯度升高,Saffman升力增加,同时温度梯度增加,导致热泳力增加,两者力的方向均指向管中心,从而导致近壁面颗粒质量浓度降低。

图7 不同热流密度下近壁面颗粒质量浓度分布(T0=310 ℃,qm=0.013 9 kg/s)Fig.7 Near-wall particle concentration distribution underdifferent heat flux densities
3.3 水的质量流量对近壁面颗粒质量浓度的影响
工况1和工况3下水的近壁面温度分布分别见图8和图9,近壁面颗粒质量浓度分布见图10。

图8 工况1下近壁面温度分布Fig.8 Near-wall temperature distribution under condition 1

图9 工况3下近壁面温度分布Fig.9 Near-wall temperature distribution under condition 3

图10 不同质量流量下近壁面颗粒质量浓度分布(T0=310 ℃,q=0.12 MW/m3)Fig.10 Near-wall particle concentration distribution at differentmass flow rates
水质量流量的变化直接影响了速度边界层中速度梯度的大小,同时也会使近壁面的温度场发生改变,从而对颗粒向近壁面的扩散产生影响。由于质量流量增大,跨临界点的位置将逐渐向出口方向移动。工况1下轴向距离0.3 m位置近壁面区域完全进入超临界态,因此在图10所示轴向距离0.3 m位置出现颗粒质量浓度峰值。而工况3下颗粒质量浓度峰值出现在轴向距离0.7 m位置,但峰值非常小,主要是因为水质量流量较大,造成近壁面速度梯度增加,在Saffman升力的作用下,颗粒倾向于远离壁面,从而形成较低的近壁面颗粒质量浓度。
4 结 论
(1) 通过SSTk-ω湍流模型模拟观察到近壁面区域传热恶化现象,传热恶化发生的位置与超临界层厚度有关,超临界层起始于管入口附近,并沿管轴向逐渐增厚,当超临界层温度在近壁面区域边界 (y0=26.1y+) 达到伪临界温度时,所对应的轴向位置近壁面温度最高,该位置即为跨临界点。
(2) 高热流密度会通过增加近壁面温度梯度来强化热泳效应,高质量流量会通过增加近壁面速度梯度来增加升力效应,两者所形成的作用力均指向远离壁面的方向,使得颗粒难以向近壁面扩散传质。
(3) 在跨临界区域,跨临界点与近壁面颗粒质量浓度峰值所在的轴向位置相对应,水的密度在伪临界点附近快速下降,同样会增加近壁面的温度梯度和速度梯度,但与直接改变热流密度或质量流量的作用结果不同,可能的原因是近壁面区域的边界上下流体密度梯度较大,会增加质量的传递,从而增加了颗粒向近壁面的扩散传质。
