自然风速下低雷诺数风力机翼型气动特性随机数值分析

唐新姿，袁可人，王效禹，彭锐涛

（湘潭大学机械工程学院，湖南湘潭 411105）

翼型气动特性是风力机设计决定性因素，其特性参数通常在确定性条件下获得.低风型风力机工作雷诺数较低，常年工作在地表层自然来流环境中，气流极不稳定，风速大小和风向均存在随机不确定特点，其翼型气动特性受到不确定风速影响，给风力机实际运行性能与载荷预测带来困难.研究随机自然来流对低雷诺数风力机翼型气动性能的影响，对于风电稳定可靠发展具有重要意义.

对于风力机翼型气动特性研究，目前国内外主要基于确定性工况条件进行风洞试验或数值模拟.黄宸武等[1]开展了S809 翼型低雷诺数下的气动特性风洞试验研究.Wang W C 等[2]通过风洞测试研究了有无湍流条件下风力机静动态性能.李仁年等[3]采用数值计算方法分析了翼型后缘厚度对翼型升阻力系数的影响.姜鑫等[4]采用数值模拟计算了多种工况不同曲率叶片翼型升力系数.为考虑非定常流动，朱志斌等[5]采用大涡模拟方法计算低雷诺数下翼型升阻力系数.如果直接在数值模拟中加入不确定边界条件计算耗时耗力，传统确定性气动数值分析已经不能满足实际工程需求.

为考虑不确定因素，国内外学者将传统确定性气动数值分析和不确定理论相结合，发展了不确定数值分析方法解决气动参数随机问题.如Abdallah I等[6]将数值模拟与蒙特卡洛法相结合量化翼型升阻力系数不确定性.该方法依赖于抽样数量，对于复杂流动分析计算效率不理想，计算时间较长，难以实际应用.为解决计算效率问题，董世充等[7]、琚亚平等[8]和刘智益等[9]基于谱展开法、嵌入式和非嵌入式混沌多项式方法，分别研究随机表面粗糙度对风力机翼型气动特性影响和随机失谐叶片安装角对风力机流场及气动特性影响.赵轲等[10]基于混沌多项式展开并结合数值模拟方法分析了马赫数对翼型气动性能影响.邬晓敬等[11]采用非嵌入式混沌多项式方法分析了飞行状态不确定性对翼型气动力影响.Zhong X P 等[12]与丁继锋等[13]采用多项式响应面模型进行不确定马赫数条件下翼型稳健设计.

风力机随机气动问题正受到越来越多研究者的重视，研究发现自然来流风速不确定会导致风力机理论设计与实际运行产生偏差[14]，但由于自然随机风速很难通过实验方式产生，风速大小和方向不确定双因素耦合作用对风力机翼型气动特性影响及其不确定性在流场中的传播机制亟待明确.

本文基于多项式混沌法和随机配点法以及Transition SST 湍流方程，构建随机翼型气动数值分析模型，以S809 风力机翼型为研究对象，从不确定风速大小和方向均值、方差与气动力等方面讨论随机自然来流对翼型升力和阻力不确定性影响，量化随机风速大小和方向工况下风力机翼型气动特性的不确定程度，为极限载荷和疲劳载荷分布谱分析和可靠性评估提供依据；获得随机风速条件下风力机翼型气动力确定性和不确定性成分比例，通过压力系数摩阻系数和湍动能分布揭示不确定性在流场中的传播机制，为风电叶片气动稳健性研究提供参考.

1 研究方法

1.1 低雷诺数数值分析方法及验证

在低雷诺数流动下，准确判断层流分离与转捩位置至关重要.经过湍流模型对比分析，本文采用四方程转捩模型Transition SST[15]预测层流分离.计算雷诺数为3×105，计算模型S809 翼型弦长c 为1 m，对应自然风速为4.38 m/s，采用二维“C”型结构网格，翼型上下及来流上游方向取15 倍翼型弦长，翼型下游方向取20 倍弦长作为计算域边界.采用ICEM 生成结构化网格，近壁面进行局部加密，物面法向第一层网格高度为10-5倍弦长，保证壁面处y+＜1，网格增长率为1.1，近翼面网格如图1 所示.流域左边界设为速度入口，右边界设为压力出口，压力设置为绝对压力101 325 Pa，翼面为无滑移条件.采用二阶迎风差分格式进行离散，压力速度耦合采用SIMPLE 算法，收敛精度标准均为残差小于1×10-5.

图1 S809 翼型近翼面网格Fig.1 Local grid of S809

为验证网格无关性，计算了风速4.38 m/s、风向6.11°时4 种不同网格数量的升阻力系数，计算结果对比如表1 所示.由表1 可知，网格数量达到89 700时，增加网格数量计算结果不再明显变化，综合考虑计算效率，最终确定网格总数为89 700.

表1 网格无关性验证Tab.1 Grid independence verification

为进一步验证计算方法的正确性，分别计算不同攻角下S809 翼型升阻力系数并与实验值[16]进行对比，计算结果如图2 所示.结果表明采用上述方法和网格计算所得的升阻力系数计算值与实验值在低攻角下基本一致，验证了该方法的可行性.

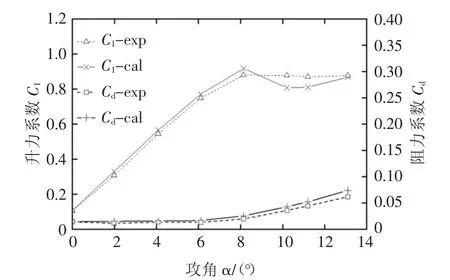
图2 S809 翼型升阻力系数实验值与计算值比较Fig.2 Comparison of calculated and experimental lift and drag coefficients of S809 airfoil

1.2 随机分析方法与验证

本文将多项式混沌法和随机配点法结合，基于Transition SST 湍流方程，形成随机翼型气动分析方法.多项式混沌法和随机配点法联合又称为非嵌入式概率配置点法（Non-intrusive Probabilistic Collocation Method，NIPRCM），参照文献[17]，得出任意样本空间上的变量关系如式（1）所示，其中yk（x，t）是由空间自变量x，时间t 和参数θ 组成的y 在第k 个配置点的值，Np为配置点的个数，hk（ξ）为对应的拉格朗日插值多项式混沌.

根据随机变量分布函数，将选取的高斯积分点及对应的求积系数映射到随机空间P 上，即得到配置点及其权重.得到权重系数后，随机变量y 的均值y 和方差σ2可以通过式（2）和（3）计算，其中yk为物理参数的确定性计算结果，wk为权重系数.

根据文献[18]可知，用公式（2）和（3）分别采用二阶与三阶方法计算翼型气动参数所得计算结果基本一致，说明二阶方法计算精度已满足要求，因此后续采用二阶NIPRCM 方法进行随机分析.

为进一步验证所采用的随机分析方法，分别计算在风速服从高斯分布的不确定条件下S809 翼型升阻力系数并与实验值[16]进行对比，计算雷诺数为3×105，攻角分别为1.99°、4.08°、6.11°、8.14°，标准差为10%均值，计算结果如图3 所示.采用上述随机方法计算所得的升阻力系数均值与确定性计算值基本一致，且两者与实验值吻合，验证了该方法的可行性.

图3 S809 翼型随机分析方法验证Fig.3 Validation of uncertain calculation of S809 airfoil

2 随机风速对翼型气动特性的影响

为量化风速大小随机性对风力机翼型气动性能的影响，计算雷诺数为3 × 105，典型攻角1.99°、6.11°、8.14°时风速大小标准差分别为均值的5%、10%、15%，即湍流强度为5%、10%、15%三种工况下S809 翼型升阻气动特性.

2.1 升阻特性

图4 为三种随机风速条件下攻角为1.99°、6.11°和8.14°时S809 翼型的升阻力正态分布，经无关性分析确定随机计算总频次为5 000.标准差越大，即风速随机性越大，升阻比不确定程度增加，但升阻比均值基本保持不变，且均值对应频次减少.攻角8.14°时，随机性对升阻比影响最大.由图4（c）可知，风速大小标准差σv为15%时，翼型升阻比标准差分别是标准差为5%和10%时升阻比标准差的4.15 倍和1.75 倍，升阻比3σ 不确定度为39.576 7±11.947 5.

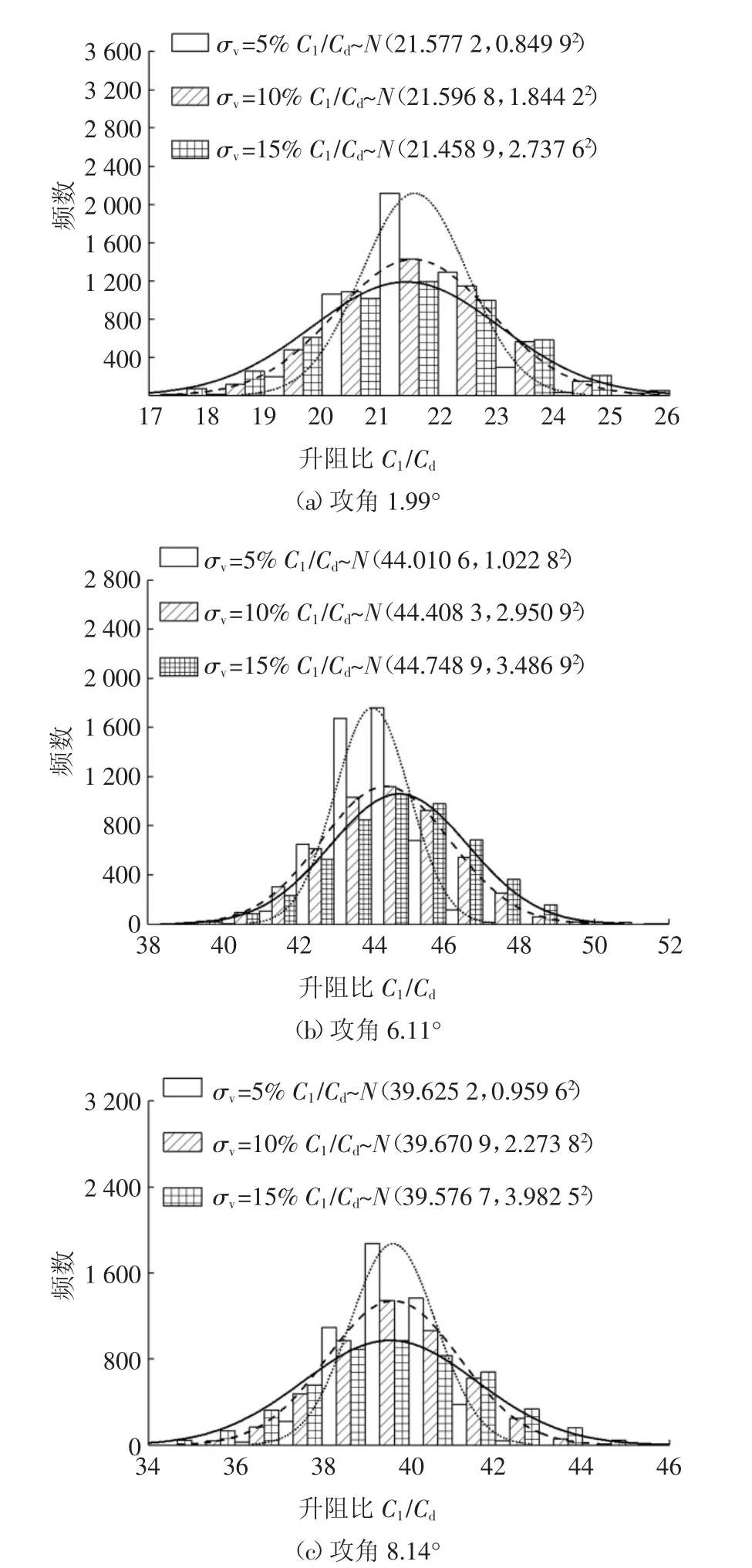
图4 随机风速下S809 翼型升阻比Fig.4 Lift drag ratio of S809 airfoil with stochastic wind speed

2.2 压力分布

图5 给出了攻角1.99°时随机风速大小条件下S809 翼型上翼面压力系数Cp的标准差分布，图中横坐标x/c 表示翼型表面点的相对弦长位置，即翼型表面点在弦长方向的投影坐标x 与弦长c 的比值.风速标准差越大，压力系数标准差峰值越大；风速大小标准差由5%增加到15%，压力系数标准差最大值由0.010 2 增加到0.047，且各标准差峰值位置始终出现在翼型0.6 倍弦长附近位置，这是由于在此位置翼型边界层出现层流分离泡[15]，流动分离转捩，对风速大小波动更为敏感.

图5 随机风速下攻角1.99°时S809 翼型上翼面压力系数标准差Fig.5 Standard deviation of pressure coefficient of upper surface of S809 airfoil at attack of angle 1.99°under stochastic wind speed

2.3 摩阻分布

图6 是攻角为1.99°时随机风速条件下S809 翼型上翼面摩阻系数Cf的标准差分布.风速大小标准差由5%增加到15%，摩阻系数标准差最大值由5.58×10-4增加到1.66×10-3.翼型前缘出现极大值，且在0.6 倍弦长附近位置再次出现峰值，规律与前述压力分布一致.

2.4 湍动能分布

图7 是攻角为1.99°时随机风速条件下S809 翼型上翼面湍动能k 的标准差分布.由图7 可知，风速大小标准差由5%增加到15%，湍动能最大标准差由1.21×10-4增加到2.91×10-4.湍动能标准差峰值始终位于翼型0.6 倍弦长附近位置，与压力和摩阻系数分布规律一致.

图6 随机风速下攻角1.99°时S809 翼型上翼面摩阻系数标准差Fig.6 Standard deviation of friction coefficient of upper surface of S809 airfoil at attack of angle 1.99°under stochastic wind speed

图7 随机风速下攻角1.99°时S809 翼型上翼面湍动能标准差Fig.7 Standard deviation of turbulent kinetic energy of upper surface of S809 airfoil at attack of angle 1.99°under stochastic wind speed

3 随机风向对翼型气动特性的影响

为分析风速方向随机性对风力机翼型气动性能的影响，在雷诺数为3×105，攻角1.99°、6.11°、8.14°工况，分别取标准差为均值的5%、10%、15%这三种风向分布，计算风速方向不确定S809 翼型气动性能.

3.1 升阻特性

图8 为三种随机风向条件下攻角为1.99°、6.11°和8.14°时S809 翼型升阻比正态分布，计算总频数为5 000.风向标准差越大，即风向随机性越大，升阻比不确定程度增加.攻角8.14°时，风向随机性对升阻比影响最大，风向标准差为15%时，翼型升阻比标准差σ 分别是5%和10%时的1.95 倍和1.18 倍，其升阻比3σ 不确定度为39.891 9±24.742 5.

图8 随机风向下S809 翼型升阻比Fig.8 Lift drag ratio of S809 airfoil with uncertain wind direction

3.2 压力分布

图9 给出了攻角1.99°时随机风向条件下S809翼型上翼面压力系数标准差分布.由图9 可知，风向标准差由5%增加到15%，压力系数最大标准差由0.032 3 增加到0.100 1.压力系数最大标准差位于前缘，翼型0.6 倍弦长附近位置出现小峰值.

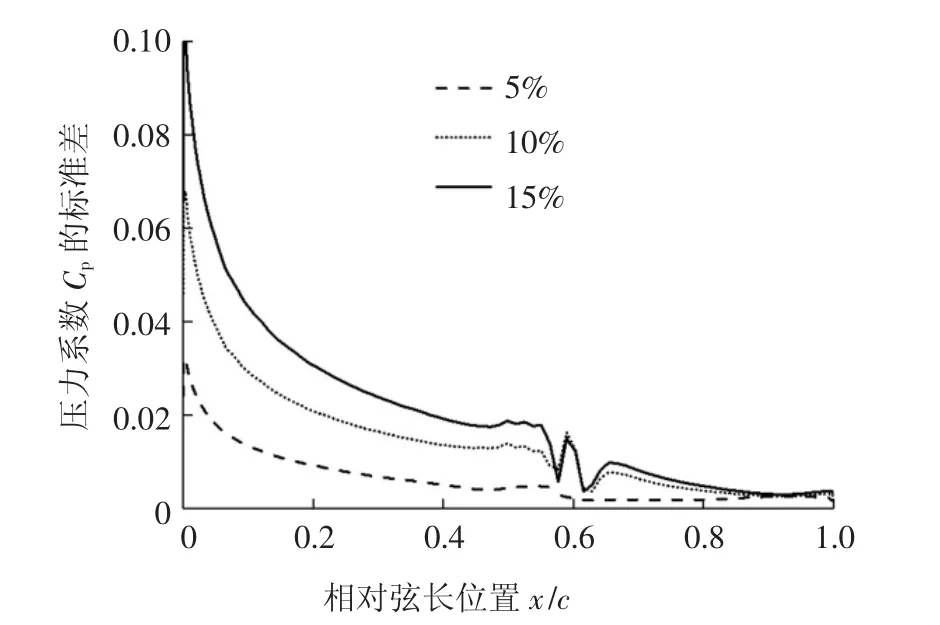
图9 随机风向下攻角1.99°时S809 翼型上翼面压力系数标准差Fig.9 Standard deviation of pressure coefficient of upper surface of S809 airfoil at attack of angle 1.99°under stochastic wind direction

3.3 摩阻分布

图10 是攻角为1.99°时随机风向条件下S809翼型上翼面摩阻系数标准差分布.风向标准差由5%增加到15%，摩阻系数最大标准差由9.29×10-4增加到2.92×10-3，最大标准差位置位于前缘，且在翼型0.6 倍弦长附近位置再次出现峰值.

图10 随机风向下攻角1.99°时S809 翼型摩阻系数上翼面标准差Fig.10 Standard deviation of friction coefficient of upper surface of S809 airfoil at attack of angle 1.99°under stochastic wind direction

3.4 湍动能分布

图11 是攻角为1.99°时随机风向条件下S809翼型上翼面湍动能标准差分布.由图11 可知，风向标准差由5%增加到15%，湍动能最大标准差由7.8 × 10-6增加到5.33 × 10-5，其峰值位置位于0.6倍弦长附近位置，敏感位置与压力摩阻系数分析结论一致.

图11 随机风向下攻角1.99°时S809 翼型上翼面湍动能标准差Fig.11 Standard deviation of turbulent kinetic energy of upper surface of S809 airfoil at attack of angle 1.99°under stochastic wind direction

4 随机风速风向耦合对翼型气动特性的影响

为分析风速和风向同时存在随机性对风力机翼型气动性能的影响，在雷诺数为3×105，攻角1.99°、6.11°、8.14°工况，各计算标准差为5%均值，计算S809 翼型气动性能.

4.1 升阻特性

图12 给出了风速、风向单随机因素以及风速和风向同时存在随机性，攻角分别为1.99°、6.11°和8.14°时S809 翼型升阻比正态分布，计算总频数为5 000.相同攻角下，随机耦合作用下的升阻比标准差大于单随机因素下的升阻比标准差.攻角8.14°时，风向不确定性对升阻比影响最大.由图12（c）可知，风速风向随机耦合作用下，翼型升阻比3σ 不确定度为39.022 3±13.708 5，即3σ 置信区间相对不确定度为±35.13%，且其标准差σv，α分别是风速（σv）和风向（σα）单随机因素时的4.76 倍和1.08 倍.

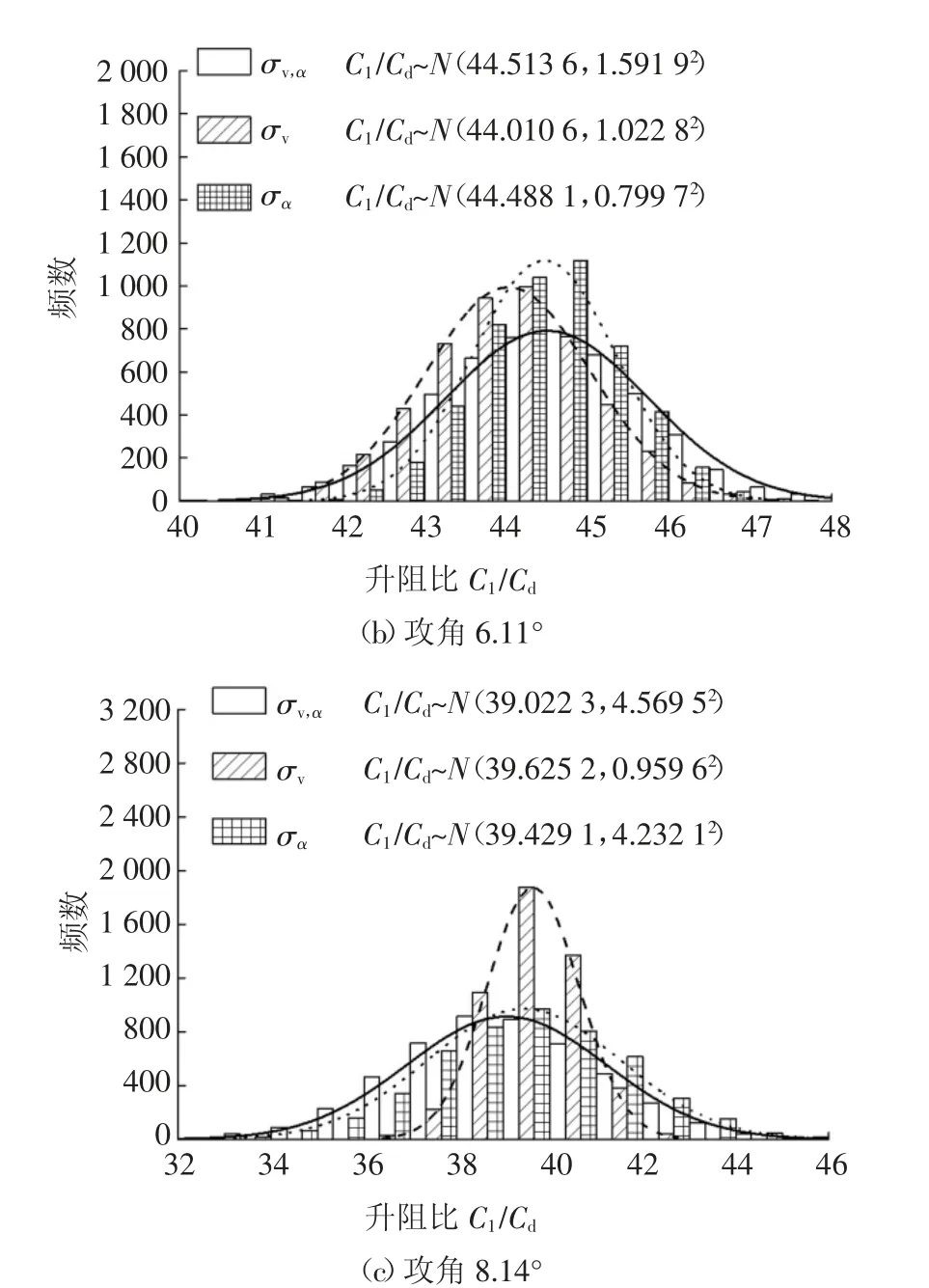
图12 随机风速风向耦合下S809 翼型升阻比Fig.12 Lift drag ratio of S809 airfoil with uncertain wind speed and uncertain direction

4.2 压力分布

图13 为随机风速、风向以及随机风速和风向耦合作用下，攻角分别为1.99°、6.11°和8.14°时S809翼型上翼面压力系数标准差分布.随机风速风向耦合作用时，压力系数不确定程度大于单随机因素影响程度；且攻角增大，压力系数不确定度增加.在随机风速和风向耦合作用下，攻角1.99°、6.11°和8.14°时压力系数最大标准差分别为0.035 2、0.214 1 和0.955 6，各压力系数标准差最大值均出现在前缘.

图13 随机风速风向耦合下S809 翼型压力系数标准差Fig.13 Standard deviation pressure coefficient of S809 airfoil with uncertain wind speed and uncertain direction

5 结论

基于NIPRCM 方法和Transition SST 转捩模型，建立低雷诺数翼型气动特性随机数值分析模型，量化随机风速大小和方向对风力机翼型升阻力和流场特性的影响，获得自然来流条件下风力机翼型气动特性不确定程度及流场非稳传播规律.主要结论如下：

1）随机风速风向对翼型升阻气动因子不确定度影响显著，且来流随机性越大升阻比不确定程度越大，在计算攻角范围内S809 翼型升阻比3σ 置信区间相对不确定度最大为±35.13%，该值远大于常规设计标准静态气动因子评估不确定度，表明风力机设计应根据实际安装位置气流状况，加强动态时变极限载荷和疲劳载荷风险评估.

2）随机风速风向耦合作用时翼型升阻力系数不确定度比随机风向或随机风速时的不确定度明显增大，且风向不确定影响更大.攻角8.14°随机风速风向耦合作用且标准差为5%时，S809 翼型升阻比不确定度分别是风速和风向单随机因素下的4.76 倍和1.08 倍.

3）在随机自然风速条件下，翼型对来流不确定性敏感区域为前缘，且中部0.6 倍弦长位置转捩处出现非稳流动加剧，可以考虑在翼型前缘部分进行气动稳健性优化设计.