基于遗传模糊算法爬壁机器人避障仿真研究

芦红利， 闫 娟， 余星宝， 路玉凤， 张雪涛， 张友朋

(上海工程技术大学 机械与汽车工程学院， 上海 201620)

随着社会的不断发展，爬壁机器人得到了飞速的发展[1-2]，其可用于桥梁检测、壁面清洗和船舶除锈等场合，代替了人在危险环境下进行作业。为保证机器人在复杂的壁面环境[3]能够正常的工作，爬壁机器人需要对壁面存在的障碍物进行及时躲避并继续工作[4-6]。

爬壁机器人避障控制属于局部避障控制[7]，不同于全局避障控制[8]。现有爬壁机器人进行局部避障的方法主要有：人工势场法[9]，分别建立运动体和障碍物、目标点的作用力，利用引力和斥力的不断作用从而规避障碍物，到达目标点。改进可视图法[10-11]，利用传感器建立目标点和障碍物的连线，运动体和障碍物的连线，通过各组连线建立可视化的数学模型，机器人避开障碍物到达目标点。模糊控制规避法[12-13]，将模糊控制器的输入设置为运动体和障碍物间的距离，从而计算出运动体的输出速度和角速度，实现规避障碍物同时到达目标点。

上述算法都能够实现机器人避障的目标，但由于爬壁机器人在运动时受到重力、壁面支撑力和吸附力的影响，同时也考虑到实际应用中隶属函数精度不高，不能很好完成实际工作的问题，课题组通过引入遗传算法，对机器人的模糊控制隶属函数和模糊控制规则进行优化。在MATALB软件中进行仿真，对遗传算法和遗传模糊控制算法进行比较，为深入研究爬壁机器人路径规划和避障控制提供参考依据。

1 机器人运动模型

1.1 机器人模型

课题组对爬壁机器人进行研究，探究其在壁面运动的避障问题，运动模型如图1所示。

图1 爬壁机器人运动模型Figure 1 Movement model of the wall-climbing robot

v为爬壁机器人的移动速度，r为运动路径，ω为自转的角速度，φ为移动角度偏差，O为运动的终点位置，M为起始位置。

爬壁机器人的角速度方程式和运动速度为：

(1)

式中：x和y为爬壁机器人在坐标系中的位置。

爬壁机器人运动路径的误差方程为

e=r-rd。

(2)

式中：rd为实际行走路径，r为理论行走路径。

1.2 路径规划

爬壁机器人的路径规划用平面栅格的方式进行表达，如图2所示。

图2 栅格与序号关系图Figure 2 Relationship between grid and ordinal

栅格中，黑色方格1，7，10，12和14表示障碍物，矩阵中用数字1表示，其余白色方格表示机器人可以通行，矩阵中用0表示。因此，可以得到对应矩阵：

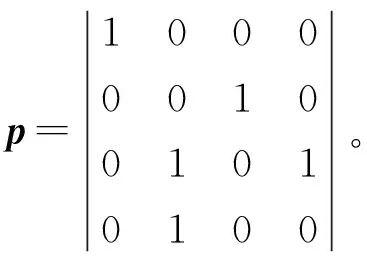
(3)

序号在栅格中映射关系为：

(4)

式中：ceil(λ/Ny)为λ/Ny整数，mod (λ,Nx)为λ/Nx的余数，λ为栅格序号，Nx为矩阵每行的格数，Ny为矩阵每列的格数。

爬壁机器人最短路径的运动方程为

(5)

式中：(xi,yi)为爬壁机器人运动起始点的坐标，(xj,yj)为爬壁机器人运动目标点的坐标。

2 基于遗传算法的模糊避障控制

2.1 模糊避障控制系统

如图3所示，模糊避障控制器[14]主要组成部分为：

1) 模糊化。将系统输入的外部参考系、系统的状态等精确量转化为模糊化量进行输出。

2) 模糊推理。利用推理的规则和逻辑关系模仿人类进行推理。

3) 清晰化。通过模糊推理得到的结果转化为进行使用的准确清晰的数字量。

4) 知识库。由模糊控制规则库和数据库共同组成，规则库包含模糊语言表示的控制规则，数据库包含模糊空间分级数、尺度变换因子和隶属函数。

图3 模糊控制器的结构图Figure 3 Structure of fuzzy controller

2.2 隶属函数

隶属函数2个输入量为：角度β和距离D。距离是前进方向上智能体和障碍物之间的长度。角度为预测路径和最近的障碍物之间的夹角。{VF,F,N,VN}4个模糊值分别表示{十分近，近，远，十分远}。变量偏转角度{E,GE,G,GR,R}分别表示{左，前左，前，前右，右}。

隶属函数中所有输入和输出都为三角形的隶属函数[15]。输入隶属函数如图4所示，输出隶属函数如图5所示。

图4 隶属函数曲线Figure 4 Membership function curve

图5 偏转角和角度的隶属函数曲线Figure 5 Membership function curves of deflection angle

2.3 遗传模糊控制算法优化步骤

传统的模糊控制隶属函数是根据前人总结的经验所得，无法应用在实际的任务中[16]。课题组利用遗传算法对模糊控制进行优化，步骤为：

1) 编码方法。对模糊规则和隶属函数进行调整，采用二进制编码方式，规则位占据前25位，隶属函数为26～35位，偏转角度的隶属函数为36～45位。

2) 种群的产生。利用随机的规则生成初始的解集S={S0,S1,…,Sn}，Sn为染色体个数。

4) 算子计算。为了更好地解决进化后群体多样性减少的问题，将机器人初始集S中的S0,S1,…,Sn，按照完成时间进行排序，将完成最快的个体S0复制到下一代，剩余的排序好的个体采用线性排序选择的方式进行选择复制下一代的个体。

5) 交叉算子设计及自适应变异。利用双点交叉的方式产生下一代，即选择2个交叉点，将2个交叉点内基因进行交换，从而产生下一代。为了方便控制进化过程及进行避障，引入自适应变异算子。同时为了简化计算，将取值的变异的概率和群体的平均值联系起来，从而适应算子变异的设计。

6) 寻优和增删操作。把改进算法和寻优方法优势进行结合。将每一代适应度排名靠前的个体，在个体邻域的范围内进行随机的搜索，寻找更新最优解。为了防止遗传算法提前结束，对相似的个体进行删除操作，删除适应度小的个体后，需要对空缺的位置进行增加，上一代适应度高的个体变异后的新个体作为增加的个体。

3 仿真分析

为了验证爬壁人采用遗传算法改进的模糊避障控制的设计方案，利用MATLAB仿真平台进行测试，爬壁机器人的初始点为(0，0)，目标为(10，10)，机器人工作壁面为10 m×10 m，机器人工作壁面设置20个障碍物，并将遗传算法和遗传模糊控制仿真结果进行比较，仿真的具体步骤为：①编辑模糊推理系统；②进行输入和输出对话框的添加；③进行隶属函数的编辑，隶属函数如图6所示；④进行规则的编辑；⑤将模糊逻辑添加至Simulink；⑥运行程序。仿真结果如图7所示。

仿真结果图7中，虚线为起始点到目标点的路径，点划线为基于遗传算法的爬壁机器人避障路径，实线为基于遗传算法改进模糊避障控制的爬壁机器人的避障路径。从图7中可得出，基于遗传算法和遗传模糊控制算法都能在不碰触障碍物的前提下，完成从起始点到目标点的仿真路径。从图中可以明显看出，采用遗传模糊控制算法能够更好地跟踪起点和目标点的连线，同时实现避障操作，整个过程路径更短，实验效果更为理想。

图6 各变量隶属函数Figure 6 Membership function

图7 爬壁机器人避障轨迹Figure 7 Obstacle avoidance trajectory of wall-climbing robot

4 结语

课题组为解决爬壁机器人模糊控制精度低的问题，建立了爬壁机器人在壁面的运动模型，求解出机器人运动学方程；利用平面栅格的方式描述机器人运动路径的规划。基于遗传算法对模糊控制机器人进行优化研究，算子设计方面选择最优保留和排序选择的机制，既保留了种群最终的多样性，同时又保证了群体收敛的最佳解；在变异算子方面，加入了自适应变异算子，改善了遗传算法在避障控制方面的应用效果；增加增删操作，解决了种群多样性导致陷入局部解的问题。将MATLAB仿真实验结果与遗传算法相比较，结果表明：遗传模糊控制算法在避开障碍物的前提下，能够更好地跟踪起点和目标点的连线并规划出从起始点到目标点更短的路径。本研究可为深入研究爬壁机器人路径规划和避障控制提供参考。