基于刀具跳动的非可展直纹面侧铣加工刀位优化方法

孔 森， 张立强， 冯倩倩， 邵云龙

(上海工程技术大学 机械与汽车工程学院, 上海 201620)

高端装备的零件如航空发动机叶片、机身蒙皮等在计算机内通常用一些网格曲面构建，没有精确的计算公式。直纹面在制造业中应用广泛，其可以分为可展直纹面与非可展直纹面，其中可展直纹面加工比较简单，并不是文中研究重点；非可展直纹面由于其法向量沿着直母线方向是变化的，因此在侧铣过程中使用圆柱刀或者圆锥刀都不可避免存在加工误差。在铣削铝合金等软材料工件的直纹面时刀具跳动会对工件产生较大的误差，因此减少因刀具跳动对非可展直纹面产生的加工误差是课题组的研究内容。

为了达到更小的加工误差即得到更高精度的零件，诸多学者针对非可展直纹面的原理性误差[1]通过不同的角度和方法进行了探索。LIU[2]将曲面基线上的一对离散点进行偏置得到一组刀轴，这种方法虽然简单，但误差很大；CHIOU[3]将刀具包络面与待加工表面之间的法向距离作为优化函数，通过调整刀具位姿使误差减小；REDONNET等[4]通过复杂的算法使3点相切于工件表面以达到减小误差的目的；严涛等[5]通过4点偏置法和最小二乘法进一步对问题进行优化；BEDI等[6]提出了刀具包络面与曲面的2条母线相切的方法，忽略了直纹面中间误差的优化，使直纹面内部的误差过大；MENZEL等[7]建立了3步优化算法，3步优化后的误差较大。

在侧铣加工时，刀具按照机床的NC指令运动，刀具自身的旋转形成的刀具包络面与设计曲面形成切触线，刀具运动使切触线形成直纹面[8-9]。因此，如果刀具—工件接触轮廓存在误差，会导致零件表面产生加工误差。侧铣刀具自身的旋转产生的跳动、磨损变形等都会影响不同位置的刀具回转轮廓半径的大小，产生刀具回转轮廓误差[10-12]。在侧铣非可展直纹面的领域中，较少有人在非可展直纹面原理性误差的基础上进一步考虑刀具跳动对直纹面原理性误差的影响。

1 单刀位下误差度量函数的构造

为了提高工件的表面加工质量，需要构造优化函数。如图 1 所示，Tc为刀轴矢量；P为刀轴上的一点,PN为设计曲面在点N处的垂线，N为垂足，是垂线和设计曲面的交点；n为垂足处的法矢；M为垂线和刀具表面的交点;W为刀具表面上一点，PW为P点到刀具表面的距离。显然，加工误差为|PN|-|PW|,|PN|-|PW|越小，加工误差越小。将刀具轴线离散化，得到各个离散点处的加工误差：

ζ=|PiNi|-|PiWi|=|PiNi|-R。

(1)

未考虑刀具跳动时的单刀位误差函数为

(2)

式中：i为刀轴上某一离散点，m为所有离散点的数量，R为理想刀具半径。

图1 误差度量Figure 1 Error measure

刀具跳动会使刀具切触线发生变化，所以需要建立新的加工误差度量函数。如图1所示，刀具跳动后M点将不在原来的位置，切削位置点M径向跳动至刀具实际包络面上的K点,此时，加工误差从|PN|-|PW|变为|HJ|-|HE|,得到点H处的加工误差：

σ=|HjJj|-|HjEj|=|PjNj|-R′。

(3)

式中：j为刀轴上某一离散点，R′为实际刀具半径。

单刀位下的优化的误差函数为

(4)

式中s为离散点的数量。

在进行刀位优化时，P点为刀轴离散之后的点，视为已知点，但刀具跳动后H点的位置未知，得到H点的关键是求得K点和J点得位置。N点位置的计算方法同J点。

2 刀具实际回转轮廓半径的获取

设Ti对应的刀具回转轮廓误差为φ，采用HEXAGON蓝光非接触式3D测量仪获得加工表面法向上Ti点对应的法向轮廓误差为φ，如图 2 所示。则有

φ=Φ=R′-R。

(5)

式中，当R′≥R时，说明刀具实际回转半径大于或等于理想回转半径;当R′≤R时，说明刀具实际回转半径小于或等于理想回转半径。

图2 轮廓误差测量Figure 2 Contour error measurement

(6)

图3 搜索模型Figure 3 Search model

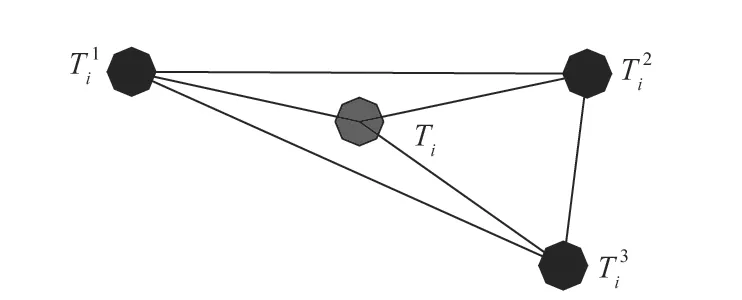
图4 轮廓误差计算模型Figure 4 Contour error calculation model

点Ti对应的实际回转半径为

Rs=R+φi。

(7)

得到实际回转轮廓半径后，可以得到J和H点的位置，从而用H点代替G点进行计算。

3 刀具跳动影响下的刀轴优化方法

3.1 初始刀位的构建

课题组通过2点偏置法确定初始刀轴两端点的位置，随后构建定点旋转算法优化刀轴位置以进一步减小误差。经验可知，刀轴数目越大，刀轴形成的轨迹面越精确，但计算效率却会下降。文中一共21个刀轴被作为初始优化目标，把单个刀轴离散为21个数据点，计算这21个离散数据的最小加工误差，从而求得单刀位下最优刀轴矢量。

3.2 单点摆动法优化初始刀位

图5 单点摆动寻优示意图Figure 5 Schematic diagram of single point swing optimization

图6 寻优示意Figure 6 Optimization diagram

4 仿真与实验

设计曲面的造型如图7所示。使用半径为5 mm的圆柱刀，并将整个设计在曲面的u方向分成[0.00,0.05]，[0.05,0.10]，[0.10,0.15]，…，[0.90,0.95]，[0.95,1.00] 20个子区域，用D=20表示，即刀轴所在参数u的位置分别等于0.00，0.05，0.10，…，0.90，0.95,1.00，计算刀轴上均布的21个点的总误差。

图7 设计曲面示意图Figure 7 Schematic diagram of design surface

如图8所示为加工现场，图9为加工完成后的零件表面。

图8 加工现场Figure 8 Processing site

图9 工件表面Figure 9 Finished products

图10为HEXAGON蓝光非接触式3D测量仪获取刀具实际回转轮廓半径的过程。HEXAGON单幅数据测量区域可达300 mm×300 mm，能快速完成零部件的表面测量。其检测效率极高，每秒钟可采集多幅影像数据，单幅数据可提供高达100万个测量点。实验中测量仪5 min内测量完零件表面，加工面扫描完成后，得到一组误差数据，把测得的误差数据代入直纹面网格节点得到误差云图。如图 11 所示为误差云图，可见在刀具跳动的影响下曲面顶端的欠切误差变化较小，误差范围为[0.001，0.010] mm；但曲面的中间部分过切误差变大并且过切的范围变大，误差范围为[-0.019,0.000] mm；曲面底端的欠切误差有所减小,误差范围为[0.000,0.004] mm。总的误差范围为[-0.019,0.010] mm,平均误差为0.016 mm。网格节点的正负误差统计后得到过切率为70.1%。

图10 测量现场Figure 10 Measurement site

图11 加工误差云图Figure 11 Machining error cloud map

得出回转轮廓误差后，计算待求的参数并通过单点摆动法减小跳动误差的影响。得到所有刀轴矢量后，把所有刀轴离散点的误差进行整理，得到误差云图，如图12所示。其误差范围为[-0.015,0.100] mm,平均误差值为0.011 8 mm。

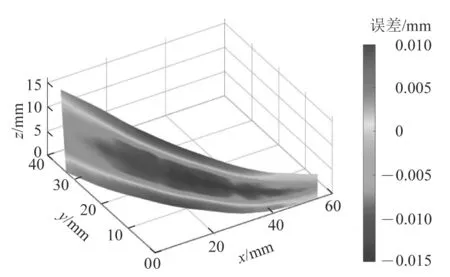
图12 仿真误差云图Figure 12 Simulation error cloud diagram

仿真工作完成后需要对工件进行切削实验及测量验证，继续用上述的实验设备加工工件，并用HEXAGON蓝光非接触式3D测量仪测量铣削误差。如图13所示，工件1为未考虑刀具跳动情况下的实物，工件2为考虑刀具跳动情况下铣削后的的实物。把测量仪所获得的点云误差数据对应在加工曲面的网格节点上，如图14所示。其误差范围为[-0.017, 0.009] mm,平均误差为0.012 mm，过切率为51.6%。

图13 加工实物Figure 13 Physical processing

图14 加工误差云图Figure 14 Processing error cloud map

如表1所示，不考虑刀具跳动时，构建定点寻优算法后，通过加工实验，得出其误差范围为[-0.019,0.010] mm,平均误差为0.016 mm，过切率为70.1%。考虑刀具跳动因素后，通过单点刀轴摆动寻优方法，零件加工后得出加工误差范围为[-0.017,0.009] mm，平均误差为0.012 mm，过切率为51.6%。2种情况对比后，可知考虑刀具跳动因素的实际加工误差范围比未考虑刀具跳动的实际平均加工误差减小了25%，过切率减小了18.5%。

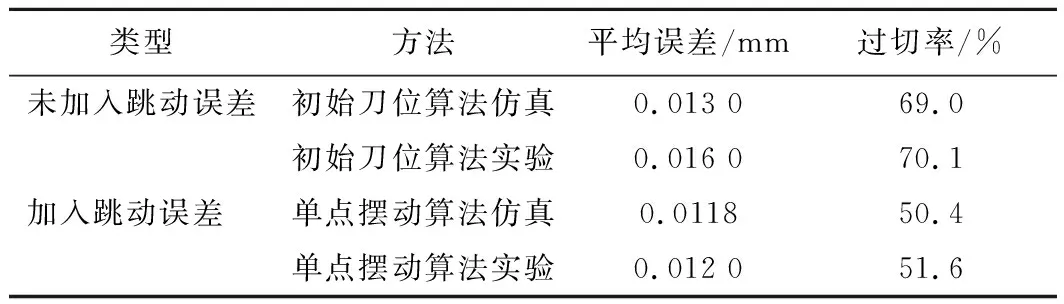
表1 误差对比

5 结语

课题组构建了非可展直纹面在刀具跳动下的新的误差度量函数，通过测量法得到实际刀具回转轮廓半径，在不考虑刀具跳动情况下通过初始刀位优化法构建了初始刀具位置；随后在考虑刀具跳动的情况下通过单点摆动法对初始刀位进一步优化。由实验对比可得平均加工误差减小了25%，过切率减小了18.5%，这对非可展直纹面的铣削加工具有一定的参考价值。