B-矩阵线性互补问题解的误差界新估计式*

李慧君, 莫宏敏, 黄家贤

(吉首大学数学与统计学院, 湖南 吉首 416000)

求x∈Rn,且满足

x≥0,Mx+q≥0,(Mx+q)Tx=0,

其中M=(mij)∈Rn×n为给定的实矩阵,q∈Rn为给定的实向量.称该数学模型为线性互补问题,记作LCP(M,q).在机械、策论、金融和数学规划等领域，线性互补问题都具有广泛应用,如期权定价和弹性接触问题等[1-3].

矩阵的结构性质关系着所在线性互补问题解的性质,为了方便LCP(M,q)的求解,设矩阵M为某些特定结构.例如,使线性互补问题具有唯一解的矩阵为P-矩阵[2].2006年,陈小君等[4]给出了当矩阵M为P-矩阵时线性互补问题的误差界:

其中：x*是LCP(M,q)的解；r(x)=min{x,Mx+q}，表示对向量x与Mx+q对应位置分量取最小；D=diag(d1,d2,…,dn)(0≤di≤1).

近年来,当矩阵M属于某些特殊矩阵类时,学者得到了其误差界估计式[5-13].笔者将继续讨论,并给出P-矩阵的子类B-矩阵线性互补问题解的误差界的一个新估计式.

1 预备知识

设A=(aij)∈Rn×n,N={1,2,…,n},若

则称A为严格对角占优矩阵[14];若aij≤0(i≠j),则称A为Z-矩阵[14];若A为Z-矩阵且A-1≥0,则称A为M-矩阵[14].

定义1[15]设A=(aij)∈Rn×n,若对于∀i,j∈N,且i≠j,有

则称A为B-矩阵.

2009年,García-Esnaola等[8]给出了当矩阵M为B-矩阵时,线性互补问题解的误差界估计式:设M=(mij)∈Rn×n是B-矩阵,且M=B++C,其中

(1)

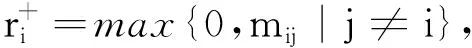
(2)

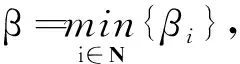
2016年,李朝迁等[13]得到了优于(2)式的新估计式:设M=(mij)∈Rn×n是B-矩阵,且M=B++C,其中B+=(bij)形如(1)式,则有

(3)

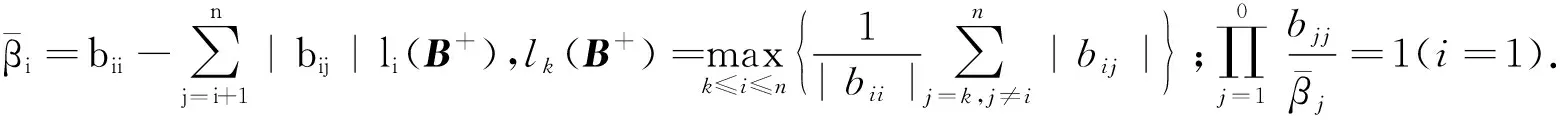
2 主要结果及其证明

令A=(aij)∈Rn×n,对于∀i,j∈N,记

引理1[16]设A=(aij)∈Rn×n是严格对角占优M-矩阵,则有

引理2[11]设γ>0和η≥0,则对于∀x∈[0,1],有

且

引理3[12]设A=(aij)∈Rn×n,且

则对于∀xi∈[0,1],i∈N，有

定理1设M=(mij)∈Rn×n是B-矩阵,且M=B++C,其中B+=(bij)形如(1)式,则有

(4)

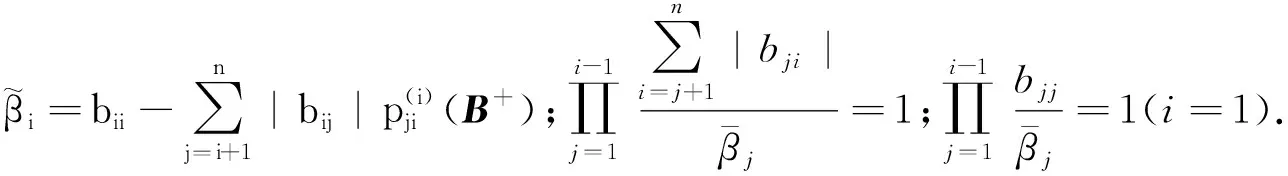
证明令MD=I-D+DM,则

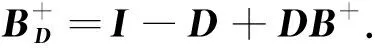
(5)

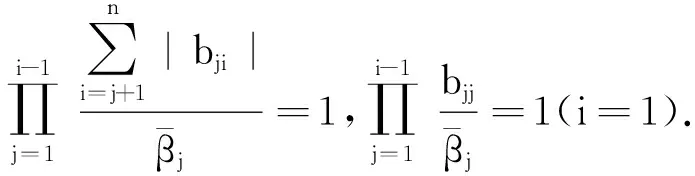
由引理2可知,对于∀i,j,k,m∈N,有

由于

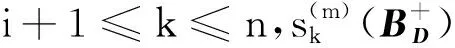
因此

进一步得到

(6)

(7)

且

(8)

由(6),(7)和(8)式可得

(9)

由(5)和(9)式可知(4)式成立.证毕.

定理2设M=(mij)∈Rn×n是B-矩阵,且M=B++C,B+=(bij)形如(1)式,则有

证明由B+是严格对角占优Z-矩阵,存在(B+)-1≥0,即B+是严格对角占优M-矩阵.对于∀i∈N,有

(10)

由(10)式可得

(11)

由(11)式，对于∀i∈N,有

(12)

则对于∀j=1,2,3,…,n-1,有

(13)

由(12),(13)式可得

证毕.

3 数值算例

例1考虑B-矩阵[13]:

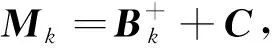
利用(2)式可得

于是

30(k+1)→+∞k→+∞.

(14)

利用(3)式可得

(15)

利用(4)式可得

(16)

易证(16)式优于(15)式.

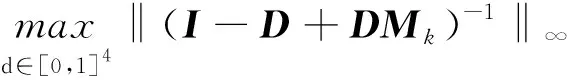
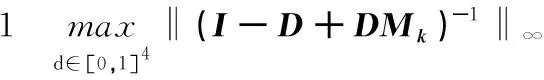
表的误差界序列

由(14)式和表1可知,(4)式优于(2)式和(3)式.这说明,定理1的误差界估计式在一定条件下优于文献[8，13]中的结果.