分岔隧道过渡段爆破对中隔墙振动响应的数值分析*

乔青青 雷胜友 杨 瑞 孙卫涛 石 磊

(长安大学公路学院1) 西安 710064) (中铁七局集团西安铁路工程有限公司2) 西安 710032)

0 引 言

分岔隧道作为一种特殊的隧道结构形式，一般包含大断面隧道、连拱隧道，以及小径距隧道间的过渡，具有连拱隧道和小净距隧道的特点[1-2].由于分岔隧道过渡段涉及的隧道结构形式较多，使得整个过渡段施工，工序复杂且相互干扰较大，尤其采用爆破法施工，更是对分岔隧道设计与施工提出了更高要求.

目前关于分岔隧道的研究多集中于隧道施工支护方案优化、围岩受力变形特征，以及爆破荷载作用下衬砌振速变化规律等方面[3-7]，而以中隔墙和中夹岩为主的研究也是多集中在位移、受力等方面，鲜有针对分岔隧道中隔墙在爆破荷载作用下振速变化规律的系统研究.李术才等[8]对中墙的稳定性判据和合理厚度进行了研究.朱道建[9]提出了分岔隧道过渡时的转变步骤和相应的计算方法.蔚立元等[10]从过渡段的位移和应力出发对分岔隧道进行了数值分析及地质力学模型试验.中隔墙是分岔隧道连拱段的关键受力构件，在隧道开挖产生的多次爆破振动波的冲击下，极易开裂破坏，从而影响隧道结构安全.因此，文中针对包湾村分岔隧道工程，采用数值模拟方法，研究分岔隧道连拱段及过渡段左、右线正洞爆破施工过程中，中隔墙及中夹岩的振动响应规律.

1 动力时程分析参数

依据道路设计规范的地基反力系数来计算曲面弹簧系数，定义弹性边界，进行特征值分析.通过计算相应土体X，Y，Z方向上的阻尼比来定义黏性边界，建立时程分析的边界条件.一般耦合装药的爆破压力都加载在孔壁的垂直方向上，爆破荷载采用国内外采用最多的爆破模型.各计算公式及参数的解释为

(1)

(2)

(3)

式中：Ax，Ay，Az为X，Y，Z方向上模型的截面面积；E0为地基的弹性系数；kx，ky，kz为X、Y、Z方向上模型的地基反力系数；α为系数，取为1.

(4)

(5)

p(t)=A0f(t)

(6)

(7)

(8)

式中：p(t)为每1 kg装药量的动压力；A0为在不耦合装药下的初始峰值应力；f(t)为指数型的时间滞后函数；db为炮孔直径；dp为破碎区范围，一般dp=2.5db；sb为炮孔间距；ρ0为炸药密度；D为炸药爆速；α为衰减指数，根据经验取2.2；n和m为由距离决定的量纲一的量阻尼参数，根据经验取m=0.055，n=0.035；f0为量纲一的量，使得在爆破冲击波上升时间结束时函数f(t)达到最大值1.0.

2 工程概况

阳安二线直通线上的包湾村隧道位于陕西省安康大巴山低山区.本文研究段起讫里程为左线XDzK235+788—XDzK235+868和右线XHK235+788—XHK235+868，平面图见图1.

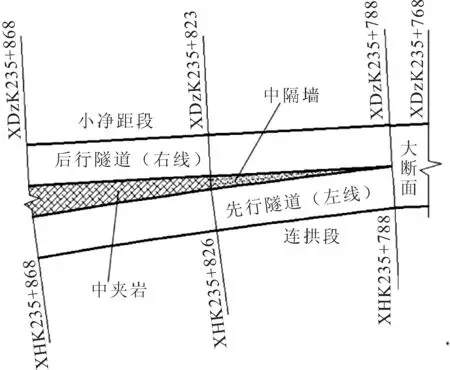
图1 包湾村隧道分岔过渡区平面图

研究段分岔隧道全长80 m，其中连拱段隧道为IV级围岩，共计38 m，中隔墙的宽度变化为0.89～3.6 m；小净距隧道为IV级围岩，共计42 m，中夹岩的宽度变化为3.6～6.95 m.

连拱隧道段正洞采用上下台阶钻爆法开挖.根据该爆破段专项施工方案，爆破进尺为2 m，炸药采用2号岩石乳化炸药，炸药密度ρ0为1.1 g/cm3，药卷直径dc为32 mm，炮孔直径db为40 mm，炮孔间距sb为450 mm，炸药爆速D为4 500 m/s，上台阶装药量为43.15 kg.

3 模型建立

通过Midas-GTS有限元软件建立三维模型，采用混合网格划分，整体模型见图2a).建立的模型由土体、大断面、连拱段、小净距段组成，Y方向包括部分大断面隧道、全部连拱段隧道、部分小净距隧道，见图2b).模型长、宽、高为隧道开挖直径的3倍，分别为120，100和116 m.连拱段及小净距段采用上下台阶爆破开挖模型，爆破进尺为2 m.依次给模型两侧、前后表面、底部添加X，Y，Z方向的地基反力系数.为简化计算，在模拟过程中将围岩视为服从莫尔-库伦准则的连续介质，且只考虑爆破荷载和自重荷载.

图2 模型结构及网格划分

3.1 模型参数

在高应变率、爆破冲击作用下需要对模型参数进行修正，结合以往研究成果[11-12]，依据实际工程参数修正后的模型参数见表1.

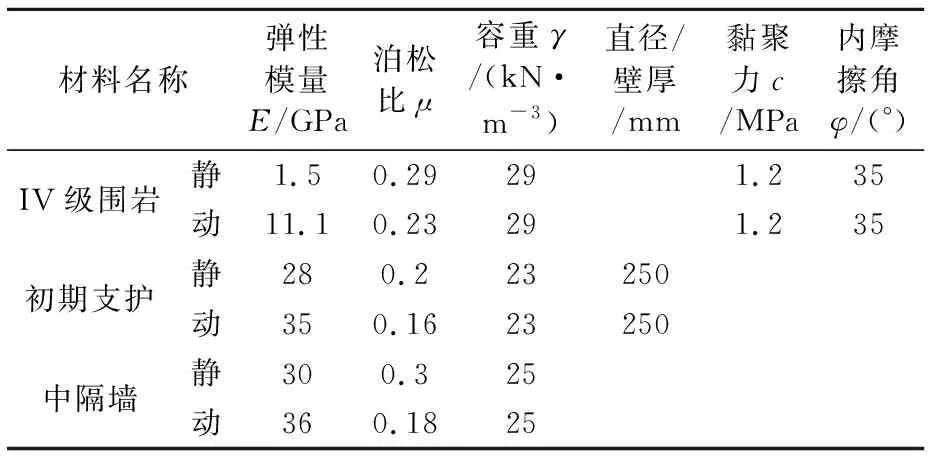
表1 模型参数

洞内初期支护采用C25喷射混凝土，中隔墙采用C30混凝土.依据式(1)～(4)得到动力时程分析参数见表2.

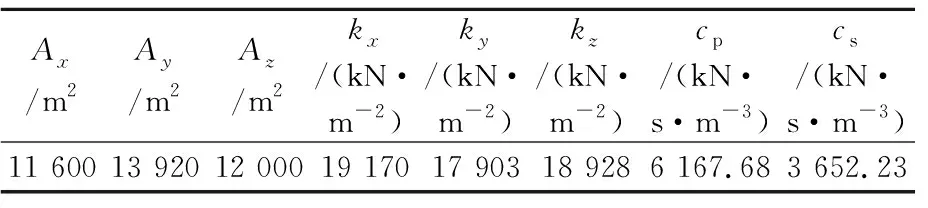
表2 动力时程分析参数

3.2 特征值分析

模型四周及底部设定相应地基反力系数，建立弹性边界，振动数量取10，运行后得到1阶和2阶振型特征周期为1.035 580和0.839 870 3 s.

3.3 时程分析

考虑在Midas-GTS中建立爆破孔单元的不易性，故在将全部爆破孔集中按照一个位置处理，爆破荷载按照一般耦合装药产生的爆破压力加载在爆破孔壁的垂直方向上[13].根据式(8)和相应爆破参数，可得爆炸冲击波峰值为32.9 MPa，孔壁动压力随时间的变化函数为

p(t)=230.053×(e-2 625t-e-4 125t)

(9)

模型四周及底部进行X，Y，Z方向的位移约束，并相应建立粘性边界.爆破荷载按照一般耦合装药产生的爆破压力加载在孔壁的垂直方向上.选取加载时间为1 s，分析时间步距为0.001，结果输出时间步长为1，共计输出1 000步计算结果，爆破荷载时程曲线见图3.

图3 爆破荷载时程曲线

3.4 建模工况及测点布置

在左、右线正洞各布置了4处爆源，分别为0，15，32.5和38 m，其中0 m爆源位于大断面隧道转连拱隧道的过渡段处，38 m爆源位于连拱隧道转小净距隧道的过渡段处，其余两处爆源位于连拱段，见图4.模型共取11个监测断面，其中沿中隔墙初始位置分别隔0，8，15，25，32.5，38 m取一个监测断面，从中夹岩开始，每4 m取一个监测断面.每个监测断面按照图5布置测点，1号测点位于断面的上部，2号测点位于断面的中部，3号测点位于断面的下部.以下分析中，规定相对距离0 m为中隔墙初始位置，相对距离38 m为中隔墙结束位置.

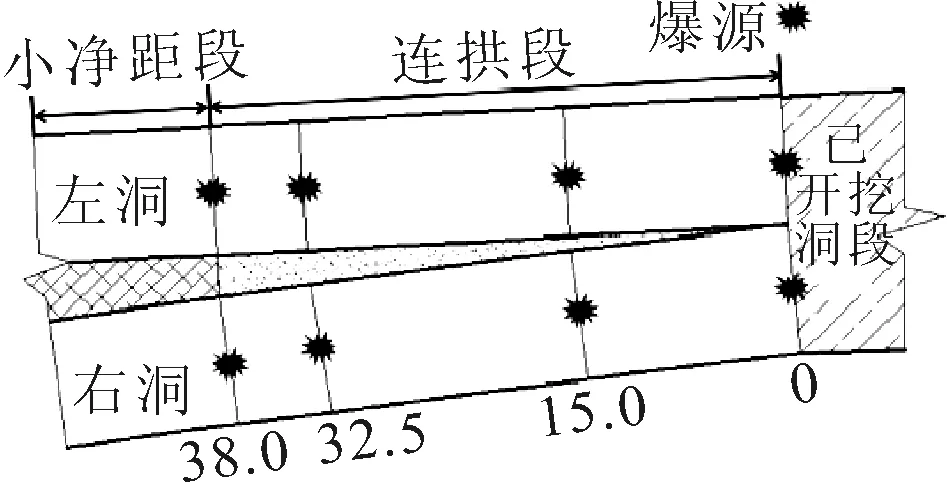
图4 爆源布置示意图(单位：m)

图5 横截面测点 布置图

4 中隔墙振动特征分析

依据文献[14]，交通隧道在振动频率F≤10 Hz时，质点的安全允许振速为10～12 cm/s，本文选取不同方向的最大振速与最严格的安全允许振速(10 cm/s)进行对比分析.

4.1 左线爆破对中隔墙的振动影响分析

图6为左线不同爆源爆破时中隔墙整体最大振速云图.由图6可知，沿中隔墙截面方向，各爆源处中隔墙左侧(迎爆侧)振速与右侧(背爆侧)振速的差值随着中隔墙厚度的增大而逐渐增大，最大差值约为5 cm/s；沿洞身方向，各爆源位置振速较大，最大值分别为22.32 cm/s(0 m爆源)、7.185 cm/s(15 m爆源)、9.64 cm/s(32.5 m爆源)和8.15 cm/s(38 m爆源).当爆源距离为0 m时，中隔墙主要危险区域(振速大于10 cm/s)大概在0～15 m范围内.当爆源距离分别为15，32.5和38 m时，中隔墙各处振速均在安全允许振速范围内.

图6 左线不同爆源爆破时中隔墙最大振速云图

表4为各爆源所对应中隔墙断面处3个测点不同方向的振速.由表4可知，各测点Z向(中隔墙竖向)振速最大，且中隔墙同一竖截面上部(1号测点)振速最大，中部(2号测点)振速最小，其中38 m爆源处上部和中部测点振速差值最大，为2.187 cm/s，15 m爆源处差值最小，为0.043 cm/s，差值沿整体中隔墙表现为两侧大中间小；X，Y向(中隔墙切向和径向)振速在中隔墙下部测点最大，X向在上部测点振速最小，Y向在上部和中部测点振速较小，X向最大振速与最小振速的差值平均为3.708 cm/s，Y向最大振速与最小振速的差值平均为0.912 cm/s.

表4 各爆源所对应中隔墙断面处3个测点不同方向的振速

结合表4数据研究规律，分别取X向、Y向和Z向振速为最大值的测点，即3号测点的X向和Y向振速，1号测点的Z向振速，进一步总结不同爆破里程下，中隔墙各向振速整体变化情况.图7为左线不同爆破里程中隔墙不同方向的振速对比图.

图7 左线不同爆源点爆破时中隔墙振速对比

由图7可知，当左线0 m处爆破开挖时，中隔墙各测点振速明显高于其他爆源处的振速，且有部分测点Z向振速超出了最大安全允许振速，主要原因是中隔墙初始位置墙壁厚度最薄，最容易发生破坏.从整体上看，会发现连拱段正洞爆破初始施工后，Z向振动速度明显大于X向和Y向振动速度，因此在整个隧道施工中，可以将中隔墙Z向振速作为主导振速，重点监测，同时做好中隔墙顶部和底部破坏控制薄弱部位的加固及监测工作.

连拱段中隔墙到小净距段中夹岩是分岔隧道的重要过渡段之一，为更好研究此处爆破施工时，中隔墙到中夹岩的振速变化规律，图8为不同测点Z向振速随中墙厚度变化图.观察发现该过渡段爆破时，中隔墙段测点的振速曲线斜率的绝对值明显大于中夹岩段，中夹岩段振速下降较中隔墙段缓慢，以中隔墙结束断面为分割线，左右相同距离处，中夹岩断面处的振速是中隔墙断面处振速的3倍，同时中隔墙各测点振速相差不大，厚度为3.6～4.6 m范围内的中夹岩段各测点振速有明显差异，其中上部振速最大，下部振速最小，两者差值最大为2.7 cm/s.

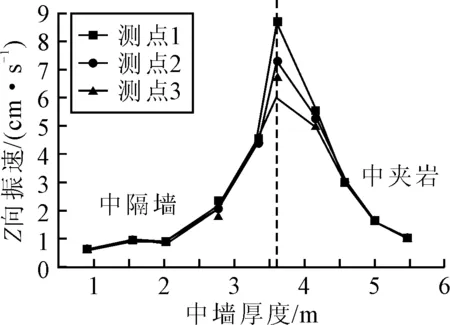
图8 过渡段不同测点的Z向振速随中墙厚度变化关系

4.2 左右线爆破对比分析

左侧正洞开挖及初期支护完成40 m之后对右线不同里程进行爆破模拟，并对各爆破里程的相同测点振速进行对比，图9为左右线不同爆破里程的中隔墙Z向振速对比图.

图9 左右线不同爆破里程Z向振速对比

由图9可知，在右线施工过程中，相同里程爆源爆破荷载作用下的中隔墙整体振速变化趋势相同；当爆源在0和15 m时，右线爆破施工相较左线爆破施工，测点振速有小幅度增加，平均增加1 cm/s，左右线爆破振速值在中隔墙后13 m基本不变，可能是右线爆破模拟时中导洞的左侧初期支护已经拆除，而导致右线爆破时相同测点振速有所增加；当爆源在32.5和38 m时，右线爆破施工相较左线爆破施工，测点振速反而呈现回落趋势，减小量最大为1.5 cm/s左右，左右线爆破振速值在中隔墙前15 m范围内基本相同，主要原因是随着中墙厚度的增加，右线爆破对中隔墙的影响范围变小.

4.3 同侧隧道前后爆破对比分析

为更好地观察同侧隧道已开挖段与未开挖段的中隔墙振速变化情况，以爆源所对应中隔墙断面为分界面，取中隔墙前后等距离位置处的振速进行对比.图10为15和32.5 m爆源处Z向振速的细节对比图，由图10可知，对比爆源前后5 m位置处的振速，左线15 m、右线15 m、左线32.5 m及右线32.5 m的同侧未开挖处的振速相比已开挖处的振速扩大了1.1，1.35，1.4，1.5倍，即同侧先开挖段的测点振速相比未开挖段的测点振速约增大1.3倍，且扩大效应在右线开挖时更加明显.

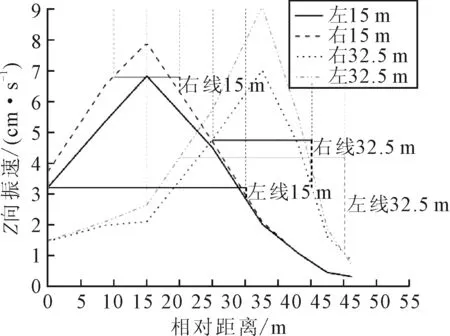
图10 左右线振速的扩大效应

4.4 不同过渡段爆破对比分析

本文研究的包湾村分岔隧道工程，施工过程中的重要节点为两个过渡段：①由大断面隧道转连拱隧道(过渡段I)；②由连拱隧道转小净距隧道(过渡段II).多种隧道形式的转换使得过渡处的稳定性十分复杂，因此有必要重点分析两个过渡段处中隔墙的振动变化规律.

由表4可知，左线正洞爆破开挖时，中隔墙在过渡段I的最大振速是1号测点的Z向振速，为22 cm/s，在过渡段II的最大振速是1号测点的Z向振速，为8.7 cm/s.两处过渡段的最大振速均位于中隔墙的上部，且均为Z向振速.从振速数值上看，大断面向连拱段的过渡施工对中隔墙的影响更大.主要由于过渡段I的爆破临空面更大，且此时的中隔墙厚度最小.在实际爆破过程中要严格控制装药量，周边眼采用不耦合间隔装药结构，其余炮眼采用连续装药，注意监测此段中墙测点的振速变化情况及爆破效果，及时调整钻爆设计参数.

选取左右线各爆源处中墙Z向最大振速，分别得到左、右线不同爆源处中墙Z向最大振速与厚度的拟合关系曲线见图11.由图11a)可知，中墙Z向最大振速与中墙厚度呈负指数关系，当振速为10 cm/s时，中墙厚度为1.1 m，即在中隔墙的前6.5 m，Z向振速大于安全允许振速.右线的拟合关系类似于左线.由图12b)可知，当振速为10 cm/s时，中墙厚度为1.65 m，即在中隔墙的前10 m，Z向振速大于安全允许振速.将左右线的危险区域对比来看，右线的危险区域比左线的要略大一点，主要原因是因为左线爆破时中导洞的左侧初期支护已经拆除，而导致右线爆破时测点振速有所增加.综上所述，在左右线的危险区域范围内，为减小对中隔墙的影响，需要考虑通过控制单段装药量、炮孔进尺深度及采用预裂爆破等措施控制爆破.

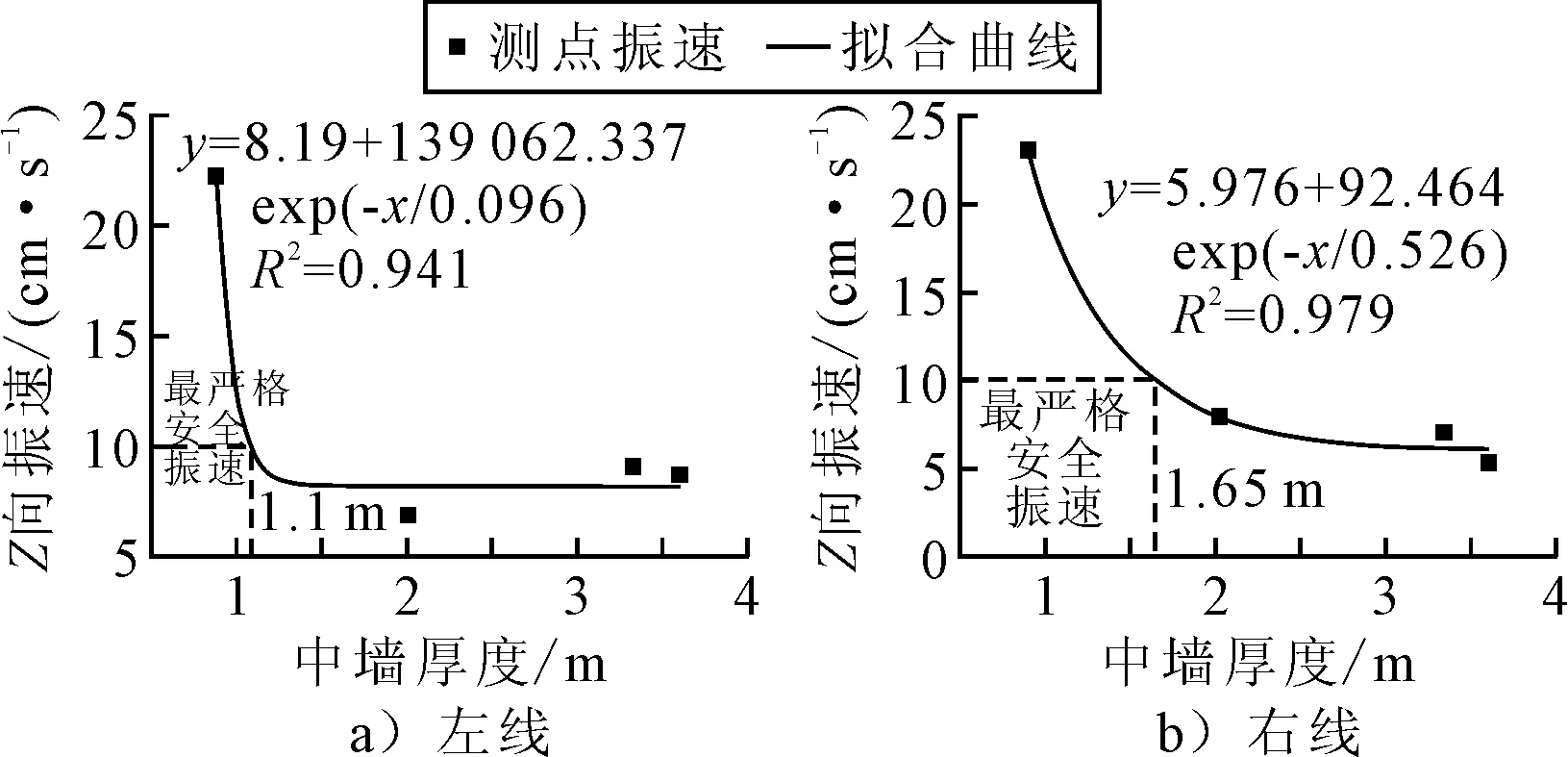
图11 Z向最大振速随中墙厚度的衰减关系曲线

5 结 论

1) 沿中隔墙横截面方向，各爆源处中隔墙迎爆侧振速与背爆侧振速的差值与中隔墙厚度成正比；中隔墙的竖向振速明显比切向振速和径向振速要大，中部振速最小；在施工监测时，应将中隔墙竖向振速作为主导振速，并确保中隔墙顶部和底部部位的施工质量.

2) 对比同侧隧道前后段的爆破作用，同侧隧道未开挖段中隔墙振速比开挖段中隔墙振速会有一个放大效应，放大倍数约1.3倍，且扩大效应在后行隧道开挖时更加明显.对比左右线隧道的爆破作用，后行隧道爆破施工对中墙的破坏作用更大；对比两个过渡段的爆破作用，大断面向连拱段的过渡施工比连拱段向小净距段的施工对中隔墙的影响更大.

3) 两过渡段间的左、右线不同爆源处中隔墙竖向最大振速与厚度呈负指数关系，以最严格的安全允许振速为分界线可得到本工程中分岔隧道连拱段爆破时左右线的最危险区域为前6.5和10 m.在危险区域内，施工时可以通过严格控制单段装药量、炮孔进尺深度，从而有效减小爆破对中隔墙的影响.