基于相关向量机的城市货运量时间序列预测模型*

韦凌翔 董建军 陈志龙 王 姝

(盐城工学院材料科学与工程学院1) 盐城 224051) (南京工业大学土木工程学院2) 南京 211800)(中国陆军工程大学国防工程学院3) 南京 210007)

0 引 言

货运量对于物流需求的确定及其相关基础设施建设、各项相关政策的制定都具有重要意义，因此对货运量的研究就成为了发展物流及其相关产业的重要依据[1-3].城市货运量预测对该城市的物流园区规划与建设、港口码头设计与建设、道路交通规划与布局、城市投资引导等都具有重要作用[4-5].

城市货运量时间序列预测模型是在统计、分析和挖掘货运量资料的基础上，研究货运量变化规律，预测货运量时间序列数据趋势的一种模型[6-7].因此，开展这方面研究是城市货运需求预测和城市物流规划的基础性工作，同时也为分析城市货运量变化规律、提高预测精度提供理论依据.

国内外学者已针对城市货运量时间序列预测开展了多方面研究，城市货运量预测模型主要分为定性预测和定量预测两大类.其中定性预测方法常采用物流货运市场调查法、德尔非法等，定量预测包括线性模型和非线性模型等.线性模型主要运用时间序列法、回归分析法以及灰色预测模型等，非线性模型主要运用人工神经网络(artificial neural network，ANN)、最小二乘支持向量机、马尔科夫模型等.具体典型研究分析如下：文献[8-10]分别验证了逐步多元线性回归模型、灰色马尔可夫预测模型、时间序列模型等方法对城市货运量时间序列预测的有效性；文献[11-12]等认为传统的回归模型无法较好地显示城市货运量时间序列数据的内在相关性，证实参数之间存在非线性关系；文献[13-15]等分别构建了支持向量机(SVM)、自组织神经网络模型、改进BP神经网络模型的货流预测方法，进一步证明了城市货运量时间序列的变化呈现出某种随机波动的特征.

综上所述，城市货运量时间序列具有一定的可预测性，其产生和变化机理受到各种客观因素影响，造成其趋势特征不全属于随机性质，数据噪声中既包含线性关系，又包含非线性关系.因此，文中拟运用非线性关系的学习理论——相关向量机(relevance vector machine，RVM)[16-18]模型，构建城市货运量时间序列预测方法，有效地提高城市货运量时间序列预测精度.

1 城市货运量时序预测模型构建

1.1 城市货运量时间序列RVM预测模型数学描述

城市货运量时序预测模型监督学习的目的是应用训练数据和先验知识建立一个预测系统，输入新的时刻序列xn，输出城市货运量时间序列预测值qn.实际采集到的城市货运量序列设为tn，tn可看作未知函数q(xn,w)被方差为σ2的高斯噪声污染所至.具体函数关系为

(1)

式中：w为权参数向量，w=(w0,w1,…,wN);εn是一个相对独立且具备相同分布的高斯白噪声，并且均值为0，其方差为σ2;另外，设φi(x)≡K(x,xi)，其中，φi(x)为非线性基函数，K(x,xi)为核函数.因此，实际采集到的城市货运量序列数据tn的分布函数可设为p(tn|x)=N(tn|q(xn),δ2)，其中，q(xn)为城市货运量序列数据的平均值，σ2为城市货运量序列数据的方差，也相当于实际数据tn与其城市货运量序列数据q(xn)的算术平均值离差平方和的平均数.方差是用于检测运算数据是否比变异及变异程度高低的最首要、最普遍的指标.鉴于假设实际数据tn是彼此独立存在的，不具有依赖性，从而关于城市货运量预测的时间序列集的最大似然估计可写为

(2)

式中：t=(t1,t2,…,tN)T;Φ为N×(N+1)矩阵，Φ=(Φ1,Φ2,…,ΦN)T,Φ(xn)=(1,K(xn,x1),K2(xn,x2),…,k(xn,xN)T.

1.2 城市货运量时间序列预测模型参数确定

由于构建预测模型中存在较多参数，采用最大似然估计由式(2)得到的w和σ2易于导致过拟合，因此，依据RVM模型参数确定思路，采用稀疏贝叶斯原理对w赋予0均值高斯先验分布得：

(3)

式中：α为N+1维的超参数向量.这样，每一个权重就单独地对应一个超参数，从而控制先验分布对各参数的影响，以确保RVM模型的稀疏性.

在定义先验概率分布与似然分布后，根据贝叶斯原理，可求得所有未知参数的后验概率分布为

(4)

后验协方差矩阵与均值分别为

∑=[δ-2ΦTΦ+A]-1

(5)

μ=δ-2∑ΦTt

(6)

式中:A=diag(α0,α1,…,αN).

关于α对数边缘似然：

L(α)=lnp(t|α,δ2)=

(7)

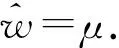
基于最大期望超参数估计，α和σ2的值可以通过迭代算法求得，在迭代学习过程中，通过式(4)～(6)可得所对应的权值w趋于0，其与预测值无关，这样就只有很少的样本点在起到作用，那些非0权值w对应的数据点被称作相关向量，体现了数据中最核心的特.

1.3 相关向量机RVM内核函数的确定

从理论上说，关于城市货运量的预测本文中可以使用任意核函数进行预测，相关向量机的内核函数选择具有随意性，可以不受任何Mercer条件约束的限制[19].但现实运用的条件下，不得不选择常用的核函数来进行计算，由于其具有普遍性，从而得到的结果也会更具有代表性.例如：线性核函数(linear kernel，LK)、多项式核函数(polynomial kernel，PK)、高斯径向基核函数(gaussian kernel，GK)等即是几种常见的内核函数.文中将构建由LK，PK，GK 此3种内核函数组成的RVM内核函数集合.

1.4 货运量时间序列预测函数的建立

如果将x*设为已知的新的输入时间序列，t*为与之相对应的城市货运量时间序列预测目标，那么相应的城市货运量预测输出的概率分布的预测函数为

(8)

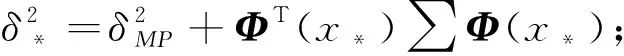
另外，连续的输入时间序列x，并且按照式q=μTΦ(x)进行计算，则可得到输出的城市货运量时间序列的预测值.

2 货运量时间序列预测模型流程与评价

2.1 货运量时间序列预测模型的流程设计

将城市货运量融入基于RVM的时间序列预测模型中，设计城市货运量预测的流程图，见图1.

图1 城市货运量预测的流程图

2.2 时间序列预测模型评价指标的确定

鉴于均方根误差(root mean square error，RMSE)是相对于原始数据的平均值而展开的，因此其能够有效的反映出预测模型误差的水平.因此，文中将选取RMSE作为评价城市货运量的时间序列预测模型精确度指标.此外，为验证模型灵敏情况选择预测模型训练时间作为指标.具体计算公式为

(9)

式中：R为RMSE.

3 实例验证

3.1 城市货运量时间序列集确定

以南京市货运总量、公路货运总量、铁路货物量为研究对象，构建城市货运量时间序列集，见图2.

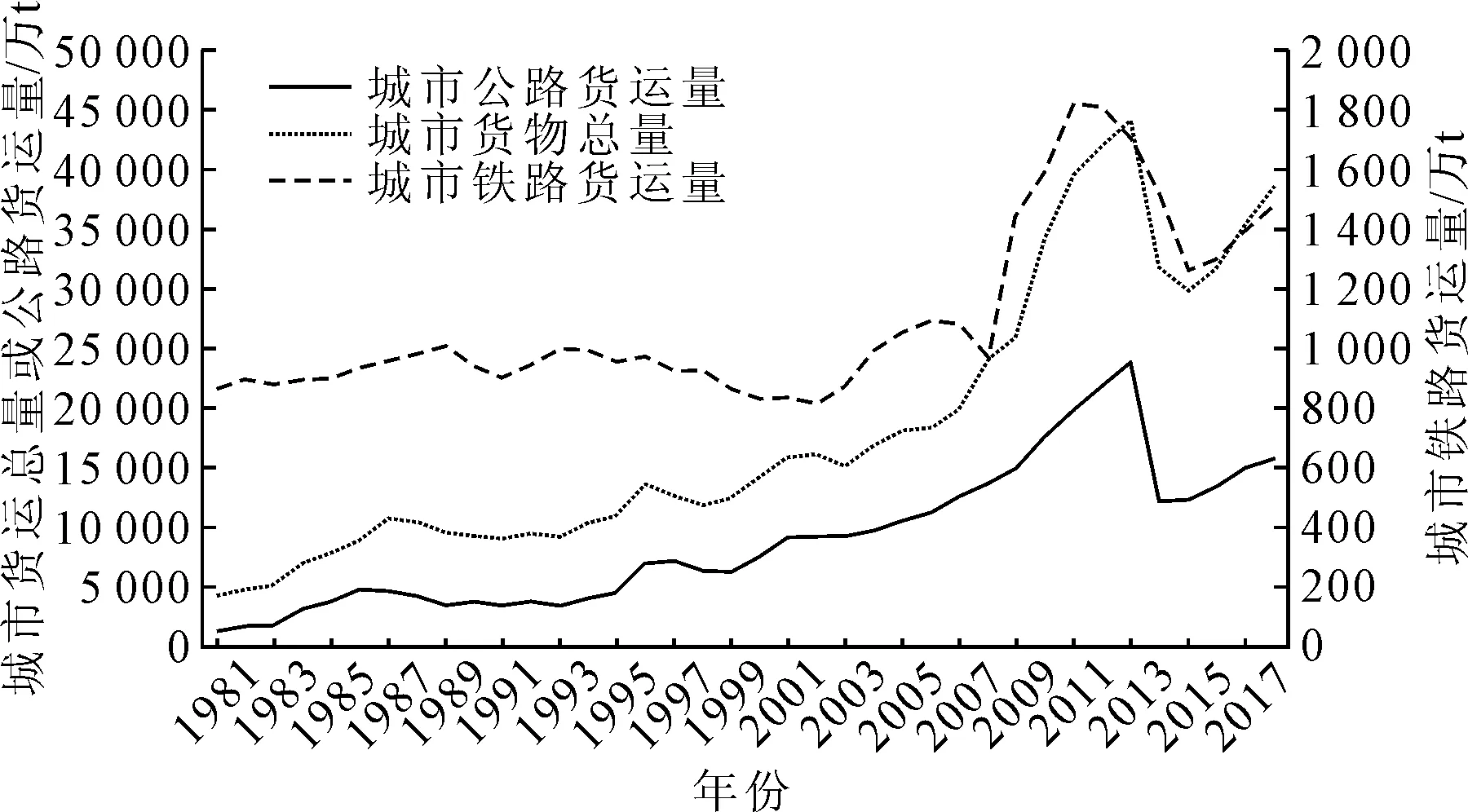
图2 南京市城市货运量数数据

3.2 城市货运量预测数据的归一化处理

数据归一化处理能有效减少函数预测中由于某数据或某数据值过大或存在量纲而导致的误差影响.因此，采用式(10)将城市货运量数据分别归一化到[0，1]区间，从而削弱RVM预测训练中带来的误差影响.

(10)

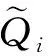
3.3 城市货运量时间序列模型的预测结果

利用Matlab，设置迭代次数的最大值为R=1 500；由于GK学习能力较强，并被广泛用于高、低维、小样本等多种情况[19]，因此可将其作为对货运量时间序列模型的预测训练，采用核函数参数ϑ=3.0的GK对该模型进行预测训练.然而，由于常用预测模型的种类具有多样性，为了体现基于RVM的城市货运量时序序列预测模型的独特性，另外选择了灰色预测模型、自回归移动平均模型(时间系列模型)、支持向量机模型(support vector machine，SVM)等3种不同类型的预测模型，对同一组城市货运量数据分别进行预测分析，得到了4组不同的RMSE数据值，对比情况见图3.

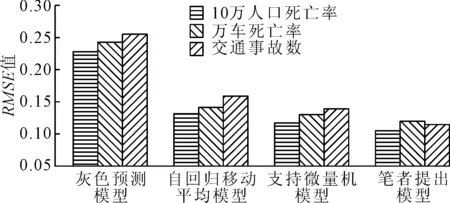
图3 4种不同模型的RMSE值对比示意图

由图3可知，对比不同城市货运量预测模型的RMSE值，基于RVM的城市货运量时序序列预测模型的RMSE值均低于其他3种模型，说明了本文提出的预测模型具有较高的预测精度及成效，能够有效的预测城市货运量的发展情况.因此，利用上述的初始参数，结合本文所研究的RVM预测模型，利用南京市货运总量、公路货运总量、铁路货物量3个指标进行训练，以预测年之前数据为训练数据、预测年的实际数据为验证数据，得到归一化后的城市货运量预测曲线图，具体见图4.输出的均方根误差值、向量机个数等预测参数值，见表1.

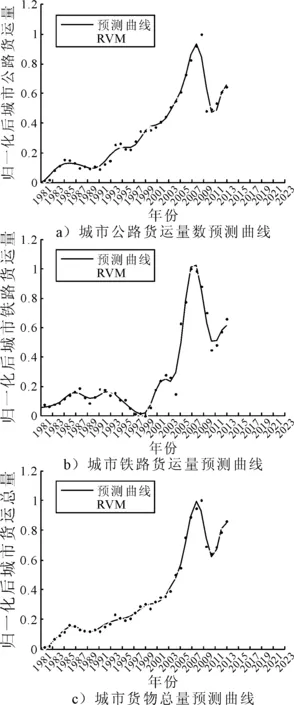
图4 城市货运量预测曲线

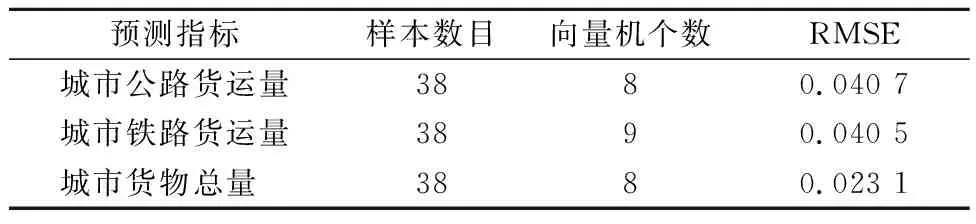
表1 本文构建模型的城市货运量预测输出相关参数

由图4和表1可知：①整体上看，该预测模型对预测城市货运量的适用性较好，对比其他3种模型，本文所研究模型对3个预测指标的RMSE值都相对较小，且试验表明该模型的训练时间较短,由此得出，城市货运量时间序列预测模型具有耗时短、精确度高、学习能力强等优势;②在不同城市货运量预测指标参数下，对比其向量机个数与样本数目有显著的差异性：样本数目明显大于向量机个数，而向量机的数量则表示预测曲线中有效的采样点.从而，该结论反映出通过少量向量机个数的变化可以分析体现出整体数据的变化趋势，进一步验证了城市货运量时间序列预测模型具有较好的稀疏性，能够有效预测城市货运量.

4 结 论

1) 本文构建的模型具有良好的预测效果，可避免由于调查数据缺失造成的预测精度降低等问题，可作为交通事故预测参考模型，为实现更为精准的城市货运量预测提供了新的理论方法.

2) 城市货运量时间序列变化趋势不仅与自身变化趋势相关，还受到城市国内经济生产总值、城市就业人数与岗位数等指标影响，因此，综合考虑影响城市货运量时间序列因素的预测模型还有待进一步研究.