环境规制如何影响就业
——基于中国省级数据的现实验证
2021-03-05宋丽颖
宋丽颖,崔 帆
(西安交通大学 经济与金融学院,陕西 西安 710061)
一、引言
为转换发展模式促进经济高质量增长、实现充分就业保障民生,近年来各级政府环境治理的政策力度不断加大,治理投入从2008年的4937.03亿元快速攀升至2017年的9538.95亿元,增幅高达93.21%;然而,在就业优先战略和更加积极的就业政策带动下,同一时期内我国就业总量从75564万人缓升至77640万人,增幅仅为2.75%。上述数据是否意味着环境治理和就业增长存在难以调和的“二元悖论”?除了就业总量,就业结构如何变动?作为社会民生关注的焦点,探究并厘清就业总量及结构在环境规制下的变动路径,对于政府治理环境污染、实现充分就业意义重大。
综观现有文献,关于环境规制与就业关系的研究虽然丰富,但结论不一。因环境质量供给不足、产权难以界定,政府利用环境规制弥补市场失灵是合理且必然的。随着规制政策的实施,一方面,劳动密集型污染企业不得不挤出部分生产性投资增加减排治污投入,生产成本的上升和利润空间的缩小导致“棕色”就业大幅下降[1]123-137;另一方面,成本约束下的企业开始倾向于用相对便宜的劳动力对污染进行有效替代。要素间的替代效应,加之政府政策的引导和消费偏好的改变,创造并提供了更多的“绿色”就业[2]313-321。在上述力量的对冲与抵消下[3]66-77,一些学者立足于成本角度,认为规制强度的提高不利于就业增长[4],[5]42-54;部分学者对此提出了质疑,认为一定条件下能够实现环境保护与就业提升的双赢[6]7-32,[7]67-73;还有学者认为,环境规制对就业的影响与自身强度有关[8]23-32,复杂的U型结构更能准确描述规制强度与就业总量的内在关系[9]54-64。
总体来看,上述研究虽然为本文提供了宝贵经验,但现有文献一方面忽略了环境规制立法、实施和监督等不同层面对就业总量的差异性影响,另一方面忽略了就业结构在规制强度变动下的发展走向。为丰富文献素材、提供新的研究视角,本文可能的创新点如下:(1)构建包含不同技能劳动力与污染要素的生产函数,对环境规制与就业规模及结构间的内在关系进行数理推导;(2)立足于教育,对教育水平如何影响环境规制下就业规模及结构的变动展开理论分析;(3)借助系统GMM,考察环境规制对不同技能劳动力就业量的差异性影响,并进一步研讨就业规模及结构在环境规制立法、实施和监督等不同层面下的具体变动。
二、理论分析
参照Cole,Elliott和Wu[10]1-408的思路,假设企业生产要素包括劳动、污染、资本和其他要素投入。生产函数形式如下:
Yit=A(Hit)α(Lit)β(K1it)γ(K2it)θ(EPit)η(Zit)φ
(1)
其中,Yit为t时期i省份污染企业的经济产出,Hit、Lit表示高、低技能劳动力的投入量,K1it、K2it为国内与国外资本投入量,EPit为污染要素投入量,Zit为其他要素投入量,α,β,γ,θ,η,φ均在0至1之间,分别表示各项投入的产出弹性系数。厂商利润可表示为:
(2)

根据厂商利润最大化原则,经求导可得:
(3)
(4)
基于上式,进一步对eit求导可得:
(5)
(6)
其中,δEP=-(eit/EPit)(dEPit/deit)为污染要素的价格弹性,也可理解为污染投入的环境规制弹性。由于环境规制越严格,污染要素越昂贵,要素投入总量越少,故dEPit/deit<0。为保证δEP非负,在其公式前加负号。

为从经济学视角对上述结论进行逻辑梳理,本文对环境规制下就业规模及结构的变动路径展开以下分析并提出相应假说:
1.环境规制与就业规模关系分析
规制强度较低时,为减轻政策变动的外生冲击,企业不得不面对污染要素成本的提高、生产性投资的挤出及减污治污投入的扩大。由此导致劳动雇佣数量的下降成为企业缓解成本压力的有效途径,即规制强度较低时,就业总量大幅下降。随着规制强度的不断提高,劳动力的价格优势逐步显现。在要素调整和结构重组的过程中,通过清洁技术的革新与生产工艺的改良,达到新的最优均衡点的企业会在利润驱动下扩大生产规模。此外,清洁产业发展下的需求替代效应也能够提供更多的“绿色”岗位。总体而言,要素替代效应与需求替代效应下显著增加的就业数量能够弥补甚至超过初期“棕色”就业的损失。故就业规模随规制强度的提高呈上升趋势。本文提出假说如下:
假说1:随环境规制强度的不断提高,就业规模呈先降后升的U型变动。
2.环境规制与就业结构关系分析
规制强度较低时,面对成本的紧约束,与作为人才投入的高技能劳动力相比,企业更倾向于减少低技能劳动力的雇佣量,即企业对劳动力需求量的下降主要表现为低技能劳动力雇佣数量的减少,说明低技能劳动力对规制强度的变动更为敏感。当规制强度进一步提高时,实现优化升级、逐步走向正轨的企业,其生产规模的扩大必然会提高对不同技能劳动力的需求,且相比于创造和掌握核心技术的高技能劳动力,无论是污染企业的增产扩产还是清洁产业的成长发展,低技能劳动力的市场需求量相对更大。总体而言,当规制强度持续提高时,虽然不同技能劳动力的就业量均有所上升,但低技能劳动力就业量的增幅更大。本文提出假说如下:
假说2:相比于高技能劳动力,低技能劳动力就业量对环境规制的强度变动更加灵敏,就业结构发生变化。
至此,本文在数理推导的基础上,就环境规制下就业规模及结构的动态变化进行了逻辑梳理。此外,在中共中央大力推进学习大国、人才强国的现实背景下,以教育水平切入,我们进一步探究了不同教育水平对环境规制与就业规模及结构关系的具体影响。
3.教育水平对环境规制与就业规模关系的影响分析
作为提升技能水平的人力资本投资,教育对就业规模的影响较为复杂。市场对高技能劳动力的需求倾向会促使更多的低技能劳动力通过接受更多的教育实现向高技能劳动力的转化。一方面,低技能劳动力的供给显著下降;另一方面,因劳动力整体优化而提升的行业生产率降低了劳动力的市场需求。无论是劳动供给量的减少,还是劳动需求量的紧缩,同等环境规制强度下,教育水平越高,就业总量越小。本文提出假说如下:
假说3:教育水平的提高不利于同等规制强度下就业规模的扩张。
4.教育水平对环境规制与就业结构关系的影响分析
一般而言,学历、受教育程度是企业筛选劳动力的常用指标。劳动力市场的需求导向、良好的社会声誉与丰厚的经济报酬使得低技能劳动力对教育水平的诉求更为强烈。相比之下,由于通过教育达到更高阶层的上升空间相对较小,教育水平的提高对高技能劳动力的吸引力较低。总体而言,低技能劳动力就业量对教育水平的灵敏度更高,就业结构发生改变。本文提出假说如下:
假说4:教育水平的提高对低技能劳动力就业量的影响更大,就业结构发生变动。
三、研究设计
(一)模型构建
1.环境规制影响就业规模的模型构建
为考察环境规制对就业规模的影响,本文构建了如下所示的动态面板模型:
jyit=β0+γjyit-1+β1enrit-1+β2enr2it-1+αXit-1+εit-1(7)Xit-1=α1lnsgdpit-1+α2lnrgdpit-1+α3lntzit-1+α4lngsit-1+α5lnldsit-1+α6lnxlit-1
(8)
其中,i代表省份,t表示时期,jyit为以t时期i省份就业量为代表的被解释变量,jyit-1为滞后项,用来控制就业过程的路径依赖。考虑到规制效果的时间滞后,本文引入了该变量的滞后期及其平方enrit-1、enr2it-1。εit-1为随机误差项。变量Xit-1为控制变量的集合。为降低模型的内生性,本文取各控制变量于时间上的滞后期,具体可见式(8)。
2.环境规制影响就业结构的模型构建
为考察环境规制对就业结构的影响,相关模型构建如下:
hjit=βh0+γhhjit-1+βh1enrit-1+βh2enr2it-1+αhXit-1+εhit-1
(9)
djit=βd0+γddjit-1+βd1enrit-1+βd2enr2it-1+αdXit-1+εdit-1
(10)
其中,hjit、djit分别为t时期i省份高、低技能劳动力的就业量,hjit-1、djit-1为对应变量的滞后值。其余指标与前文一致,不再赘述。
(二)数据说明
本文选取我国30个省份(西藏除外)2005—2016年的面板数据进行实证回归。数据主要源于历年《中国环境年鉴》《中国统计年鉴》《中国科技统计年鉴》等(4)所用数据凡涉及货币单位的,均以2005年为基期,利用我国CPI指数进行平减。对于在个别年份存在缺失情况的指标,采用线性插值法或平均增速递推法补齐。。
(三)指标选取
1.被解释变量
本文以各省城镇单位就业人数为就业总量(jy)的衡量指标;用研究与开发机构R&D人员全时当量度量高技能劳动力就业量(hj);用就业总量与高技能劳动力就业量之差测度低技能劳动力就业量(dj)。
2.解释变量
关于环境规制,学者们的度量方法不尽相同[11]37-55,[12]34-47。本文借鉴李胜兰等[13]88-110的研究思路,将环境规制划分为制定(lf)、实施(ss)和监督(jd)等不同层面。其中:制定变量由地方环境法规数(lf1)、承办人大环保的建议议案数(lf2)构成;实施变量包括环境污染治理投资占GDP比重(ss1)和工业污染治理投资占工业增加值比重(ss2);监督变量由环保系统人员充沛度(jd1)和排污费与工业增加值之比(jd2)测度。上述指标经熵值法合成后,取对数得到环境规制(enr)。
3.控制变量
本文将产业结构(第三产业产值占地区生产总值比重,sgdp)、经济发展水平(人均地区生产总值,rgdp)、社会投资水平(全社会固定资产投资,tz)、技术水平(高技术产业新产品销售收入,gs)、劳动生产率(工业增加值与就业总量之比,lds)、教育水平(大专及以上学历从业人员占比,xl)等作为控制变量引入模型。为使数据更加平稳,消除模型的共线性和异方差,取上述控制变量的对数值进行实证检验。
四、实证结果与分析
(一)环境规制对就业规模的影响分析
模型经系统GMM回归,结果可见表1:
根据上表,AR(1)、AR(2)及Sargen值的检验结果证明了模型设定的合理性和工具变量的有效性。为探究环境规制下就业规模的具体变动,根据表2:第一,由列(1)可知,环境规制二次项的回归系数在1%的水平上显著为正,表明随规制强度的不断提高,就业规模呈先降后升的U型轨迹。假说1得到验证。第二,进一步以环境规制立法层、实施层与监督层为解释变量进行回归,从立法层看,地方环境法规数与承办人大关于环保建议议案数的二次项系数均在1%的水平上显著为负,表明随立法层规制强度的提高,就业规模呈先升后降的倒U型变动。观察列(4)(5),实施层指标二次项的回归系数均至少在5%的水平上显著为正,意味着就业规模在实施层规制强度较低时下降,在规制强度较高时上升。立足于监督层,与回归系数不显著的环保人员充沛度相比,排污费/工业增加值这一硬约束与就业规模呈显著的U型关系。第三,从就业总量的滞后期看,各回归中jy的滞后项均在1%的水平上显著为正,表明上期就业量通过正向拉动当期就业水平,体现了就业规模在时间上的惯性趋势和路径依赖。
总体而言,从环境规制的整体视角看,就业总量随规制强度的提高呈显著的U型变动;从环境规制不同层面看,立法、实施、监督对就业规模的影响不尽相同。
(二)环境规制对就业结构的影响分析
分别以高、低技能劳动力为被解释变量进行系统GMM回归,结果可见表2。

表2 环境规制与不同技能劳动力回归结果
观察表2:第一,高技能劳动力的就业量不受环境规制强度变化的影响。相反,低技能劳动力的就业量对环境规制强度的变动更加灵敏,就业结构发生改变。假说2得以验证。第二,从立法层看,与变动并不明显的高技能劳动力相比,低技能劳动力的就业量随立法强度的提高呈先降后升的U型变动;立足于实施层,仅工业污染治理投资完成额与工业增加值之比在1%的显著性水平上与高技能劳动力就业量呈U型关系,低技能劳动力的就业量在环境规制实施层的影响下先下降后上升。就监督层而言,环境规制均未对高技能劳动力的就业量产生显著影响,相反,在排污费的约束下,低技能劳动力就业量呈显著的U型变动。第三,与就业规模类似,高、低技能劳动力的就业量均在时间维度上具有明显的路径依赖。
总体而言,无论基于环境规制这一整体,还是基于立法、实施与监督等不同层面,低技能劳动力对规制强度的变化更加灵敏,就业规模的U型趋势主要体现在低技能劳动力就业量的变动上。
(三)教育水平对环境规制与就业规模及结构关系的影响分析
我们假设:情景1=(lnxl-1),情景2=(lnxl),情景3=(lnxl+1),情景4=(lnxl+3),情景5=(lnxl+5),将上述各情境分别带入模型进行回归,考察不同教育水平下环境规制与就业规模及结构关系的具体变动,结果可见表3。
1.教育水平对环境规制与就业规模关系的影响分析
根据表3,一方面,不同教育水平下环境规制二次项的回归系数并未改变,均在1%的水平上显著为正,表明教育水平的高低并不会影响就业规模的U型轨迹;另一方面,观察情景1至情景5回归结果的具体差异,发现随教育水平的提高,模型的常数项不断减小。U型曲线的这一下移趋势表明,当规制强度相同时,教育水平越高,就业规模越小。假说3得以验证。
2.教育水平对环境规制与就业结构关系的影响分析
由表3可知,就高技能劳动力而言,不同教育水平下,环境规制的回归系数与显著性水平均未改变,表明教育水平的变化并不会对高技能劳动力的就业量产生显著影响。从低技能劳动力来看,教育水平虽然并未改变低技能劳动力就业量的变动轨迹,但U型的趋势曲线不断下移。总体来看,相比于高技能劳动力,教育水平使得同等规制强度下低技能劳动力的就业量明显下降,由此导致就业结构发生变动,假说4得到验证。
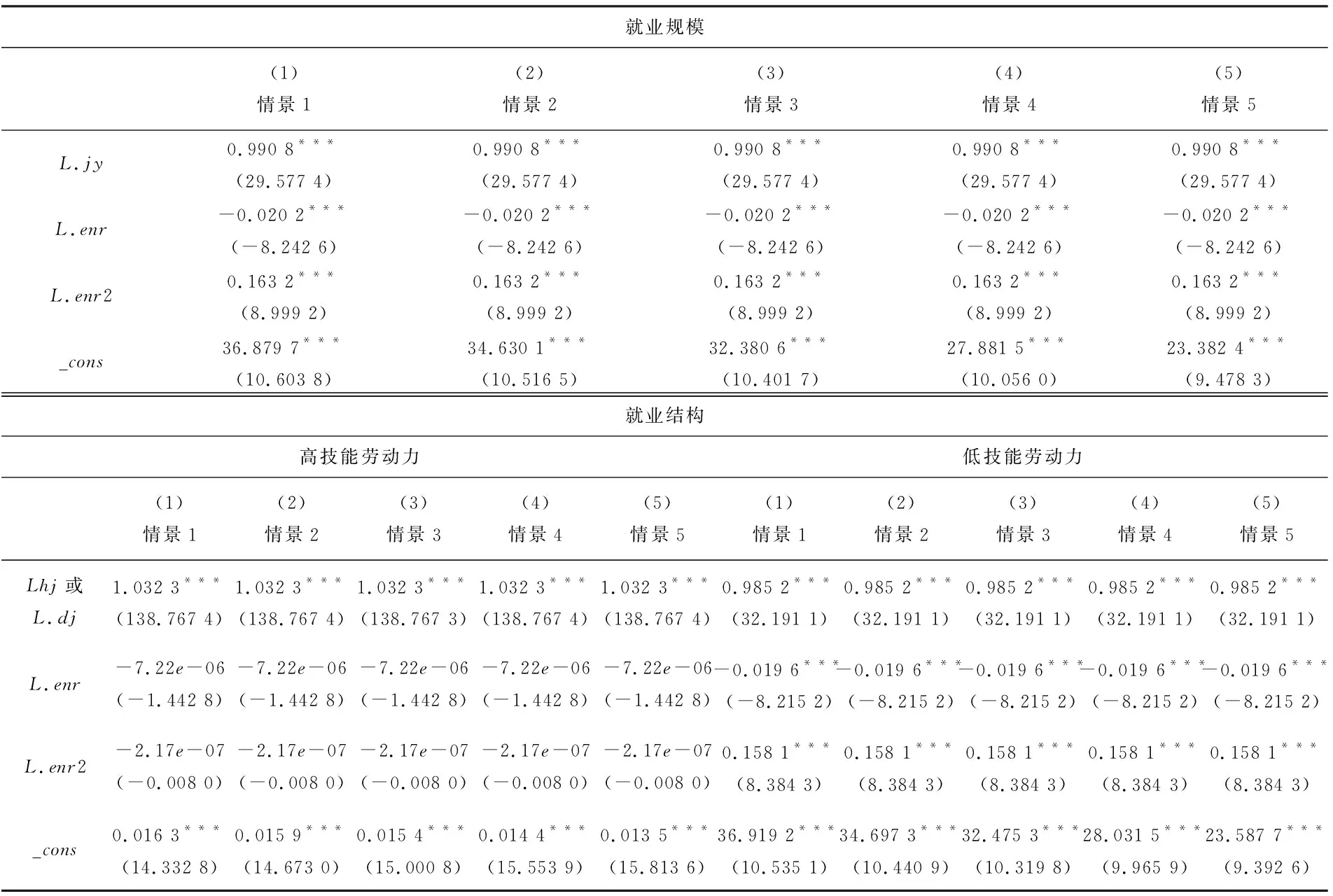
表3 不同教育水平回归结果
五、结论与展望
利用我国30个省份2005—2016年的面板数据,借助系统GMM模型,本文考察了环境规制与就业规模及结构的关系类型,并进一步对其不同层面的就业影响展开了相关研究。结果表明:(1)随规制强度的提高,就业规模呈先降后升的U型变动。(2)环境规制对高、低技能劳动力的就业量存在显著的差异性影响,就业结构发生变动。(3)同等规制强度下,教育水平越高,就业规模越小。(4)教育水平的提升对低技能劳动力的就业量影响更大,其有利于就业结构的不断优化。
需要说明的是,限于技术方法及数据的可得性,本文在以下方面有待进一步完善:一方面,鉴于数据限制,本文并未以行业清洁或污染程度为准对样本数据进行划分,即文章并未考察规制强度的变动对不同污染程度行业就业量的差异性影响;另一方面,鉴于方法限制,本文模型中的内生性问题有待进一步解决,即如何最大程度降低内生性对估计结果的影响是我们下一步研究的重难点。
