T型弯曲翼缘开孔板连接件抗剪承载力有限元分析

2021-03-04黄杨成薛东焱张益多

江苏科技大学学报(自然科学版) 2021年6期

黄杨成，薛东焱，张益多

(江苏科技大学土木工程与建筑学院，镇江 212100)

在钢-混凝土组合结构中，钢与混凝土之间的抗剪承载力是结构设计的关键问题之一[1].目前，常用的剪力连接件有焊钉剪力连接件和开孔板剪力连接件等[2].其中，开孔板连接件抗剪承载力较高，抗疲劳性能好，因而得到越来越广泛的应用[3].

为了提高开孔板连接件的抗剪性能，近年来提出了一种T型弯曲翼缘开孔板连接件.文献[4-5]通过对其进行推出试验，测试了这种连接件的基本力学性能，并通过15组极限承载力和破坏形式试验，对比分析不同参数对T型弯曲翼缘开孔板连接件承载力和破坏形式的影响.结果显示，相对于传统开孔板连接件，T型弯曲翼缘开孔板连接件具有较高的抗剪性能和良好的延性.

为进一步研究T型弯曲翼缘开孔板连接件抗剪性能的影响因素，文中将运用非线性有限元分析的方法，通过模拟推出试验，对混凝土强度、开孔板厚度、开孔直径和翼缘宽度等关键参数进行研究，得出关键参数对T型弯曲翼缘开孔板连接件抗剪承载力影响的关系方程式.

1 试验试件设计

典型的推出试验试件如图1、图2为T型弯曲翼缘开孔板细节.

图1 推出试件布置图(单位：mm)

图2 T型弯曲翼缘开孔板细节图

根据参考文献[4-5]，分析得出极限承载力影响因素主要有混凝土强度、开孔板板厚、开孔直径和翼缘宽度，将针对这4个主要影响因素进行参数分析.表1列出了17个T型弯曲翼缘开孔板连接件推出试验的试件参数.

表1 推出试验试件参数

2 有限元分析

2.1 概述

运用ABAQUS软件模拟T型弯曲翼缘开孔板连接件的推出试验，有限元模型如图3.为简化模拟过程，每个试件都选取实际试验试件的一半进行模拟，并采用静态显式方法考虑材料几何非线性.

图3 有限元模型

2.2 网格划分与网格属性

文中数值模拟的推出试验采用对称约束建模，网格划分情况如图3，其中混凝土、H型钢梁、贯穿钢筋、T型弯曲翼缘开孔板部分的网格属性为八节点线性六面体单元(C3D8R)，混凝土中结构钢筋的网格属性为二节点线性三维桁架单元(T3D2).

模型的网格全局尺寸为10 mm，在T型弯曲翼缘和对应的混凝土部分采用更精细的5 mm局部网格尺寸，同时在扭曲严重空间布置形状更灵活的四面体和楔形单元，其中四面体单元的网格属性为四节点线性四面体单元(C3D4)，楔形单元网格属性为六节点线性三棱柱单元(C3D6).

2.3 边界条件与相互作用

边界条件详见图4，面1的所有节点被限制为沿Z轴负方向匀速滑移30 mm，等效于在均布荷载作用下的滑移；面2所有节点在Y方向固定、X与Z方向的弯矩为零，其他方向自由的边界条件(U1=UR2=UR3=0)；面3所有节点在X和Z方向固定，Y方向弯矩为零(U1=U3=UR2=0).

图4 边界条件

混凝土板与H型钢梁、T型弯曲翼缘开孔板之间的切向和法向相互作用分别定义为无摩擦和硬接触.对于贯穿钢筋，采用表面-表面的绑定约束(*BINDING ELEMENT)使之与混凝土相互作用，使用ABAQUS中的嵌入约束(* EMBEDDED ELEMENT)将结构钢筋嵌入混凝土板中[6-9].

2.4 混凝土材料本构模型

文中参考ABAQUS软件中基于Lubliner以及Lee和Fenves等人提出的混凝土损伤塑性(CDP)模形[10]，混凝土材料特性为：膨胀角ψ= 30°[11-12]，偏心率ε= 0.1，双轴抗压强度与单轴抗压强度(fb0/fc0)之比为1.16，粘度参数μ为0[13-14].对于混凝土在抗压和抗拉中的材料非线性，用受压应力-应变曲线和受拉应力-裂缝宽度曲线表示.

采用如图5的混凝土本构模型.受压应力-应变曲线分为三部分.第一部分(I)为弹性阶段，比例极限应力为0.4fc，其中fc为混凝土圆柱体抗压强度.对应于峰值应力fc的应变表示为峰值应变εcp，弹性模量Ec由式(1)确定[15]：

(1)

式中：Ec为弹性模量，GPa；Ec0=21.5 GPa；αE=1；fc为混凝土圆柱体抗压强度[15].文中的混凝土强度为立方体强度，采用R.L Hermite Conversion法则[16-17]进行换算，如式(2):

(2)

式中：fc为直径150 mm，高300 mm的圆柱体强度(psi)；fcube为边长150 mm的立方体强度(psi)，1psi=6.895×10-3N/mm2.

第二部分(II)对应图5中曲线部分，应力变化范围从比例极限应力为0.4fc到峰值应力fc.该部分由式(3)确定[15]:

(3)

式中：σc为应力，MPa；k为塑性指数，k=Ec·εcp/fc；η为应变与峰值应变之比，η=εc/εcp，εcp=0.002 5；fc为混凝土圆柱体强度，MPa[15].

第三部分(Ⅲ)为线性下降段，由峰值应力fc下降到其85%，对应的应变为αεcp.经多次试算，因子α =10时较符合试验情况.

混凝土受拉状态本构模型如图5(b)，计算公式为：

(4)

图5 混凝土本构模型

2.5 钢材本构模型

文中研究重点是开孔板和贯穿钢筋，为保证结果的可靠性，建立了实体模型，同时采用了较为细致的本构模型；而混凝土中普通钢筋不是研究的重点，模型采用了简化的梁单元，同时使用了简略的本构模型以降低运算负荷.

普通钢筋本构关系如图6，计算公式为：

(5)

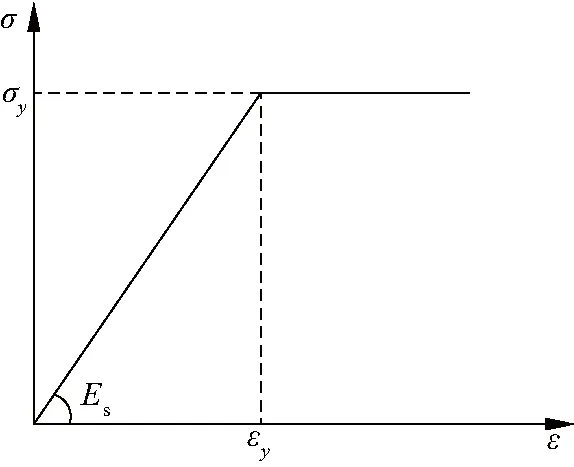
图6 钢筋应力-应变关系

式中：σy为屈服强度，εy为达到屈服强度时对应的屈服应变，Es为钢筋的弹性模量.

贯穿钢筋和钢梁的本构模型采用三线式应力-应变曲线表示[18-19]，如图7，计算公式为式(6).T形弯曲翼缘开孔板、混凝土板内的钢筋和焊钉的材料参数见表2.

(6)

图7 钢材应力-应变关系

表2 钢梁、开孔板和钢筋材料参数

3 模拟结果与分析

3.1 荷载-滑移曲线特征与验证

如图8，有限元分析得到的荷载(P)-滑移(u)曲线与试验结果拟合度较高.其中，TPS-1和TPS-2的加载方式为线性递增，TPS-3的加载方式为循环加卸载7次后，单一加载直至破坏[5].T型弯曲翼缘开孔板的荷载-滑移曲线大致可以分为三阶段：

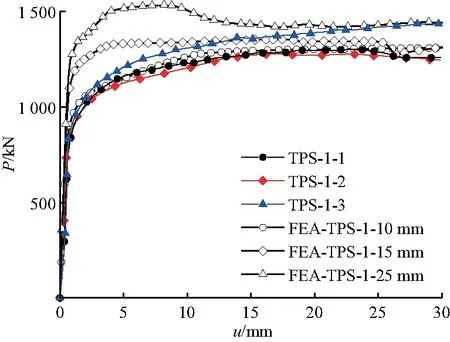
图8 荷载-滑移曲线与试验结果对比

(1) 弹性阶段：当滑移u<0.8 mm时，H型钢与混凝土相对滑移量小且增长缓慢，荷载随滑移量增大呈线性递增，结构处于弹性阶段；

(2) 弹塑性阶段：当滑移量在0.8 mm

(3) 破坏阶段：当荷载达到极值后，H型钢与混凝土相对滑移快速增长，其抗剪刚度不断下降，结构承载力缓慢下降.

为验证文中有限元分析的推出试验的可靠性，以相同条件下的实际试验为参考进行对比研究.3次推出试验结果[5]与不同网格尺寸下数值模拟结果对比如表3，取每个试件的最大荷载作为其极限抗剪承载力.其中，Qs为极限承载力，Qu，10、Qu,15、Qu,25分别为模型的全局网格尺寸为10、15和25 mm时得到的极限承载力.结果表明，当全局网格尺寸为10 mm时，数值模拟结果与实际试验的结果最为接近.

表3 分析与试验结果对比

3.2 混凝土强度的影响

如图9(a)，TPS-1、TPS-2、TPS-3、TPS-4和TPS-5构件的极限承载力分别为1 309.90、873.32、1 150.89、1 396.58、1 484.26 kN，当混凝土抗压强度从30 MPa增加到36.9、53.1、59.3和70 MPa时，极限抗剪承载力分别提高31.8%、50.0%、59.9%和67.9%.如图9(b)，拟合得到混凝土抗压强度与极限抗剪承载力关系的曲线方程为：Q=-0.35fc,t2+48.23fc,t-214.98.研究结果表明，混凝土强度对构件极限抗剪承载力有显著影响，构件极限承载力随混凝土强度的增加而增加.

图9 混凝土强度的影响

3.3 板厚的影响

如图10(a)，TPS-1、TPS-6、TPS-7、TPS-8和TPS-9构件的极限承载力分别为1 309.90、922.68、1 205.69、1 479.41、1 602.72 kN，当板厚从8 mm增加到12、16、20和24 mm时，极限抗剪承载力分别提高30.67%、41.97%、60.34%和73.71%.如图10(b)，拟合得到开孔板板厚与极限抗剪承载力关系的方程为：Q=40.85tp+650.56.研究结果表明：开孔板板厚对构件极限抗剪承载力有显著影响，构件极限承载力随板厚的增加呈线性递增趋势.

图10 板厚的影响

3.4 开孔直径的影响

如图11(a)，TPS-1、TPS-10、TPS-11、TPS-12和TPS-13构件的极限承载力分别为1 309.90、1 391.27、1 312.17、1 245.06、1 100.54 kN，当开孔直径从40 mm增加到50、60、70和80 mm时，极限抗剪承载力分别降低6.03%、6.22%、11.75%和26.42%.如图11(b)，拟合得到开孔直径与极限抗剪承载力关系的曲线方程为：Q=-0.14dh2+10dh+1 191.5.研究结果表明：开孔直径对构件极限抗剪承载力有一定影响，构件极限承载力随开孔直径的增加而降低.

图11 开孔直径的影响

3.5 翼缘宽度的影响

如图12(a)， TPS-1、TPS-14、TPS-15、TPS-16和TPS-17构件的极限承载力分别为1 309.90、1 213.68、1 303.92、1 329.03、1 393.46 kN，当翼缘宽度从100 mm增加到140、180、220和260 mm时，极限抗剪承载力分别提高7.43%、7.93%、9.51%和14.81%.