海洋石油平台舱口盖吊装冲击力学分析

沈中祥, 徐成悦, 张充霖, 袁平平, 尹 群

(1.江苏科技大学 土木工程与建筑学院，镇江 212100) (2.江苏扬子鑫福造船有限公司，泰兴 225300) (3.江苏科技大学 船舶与海洋工程学院，镇江 212100)(4.中海石油技术检测有限公司，天津 300452)

海洋石油平台舱口盖在吊装过程中引起的事故不仅会引起舱口盖和平台损坏，产生经济损失，还会对平台上作业人员的生命安全产生威胁，因此研究舱口盖吊装过程中的冲击力学问题显得非常重要.

众多学者对各种材料的冲击性能、重物的跌落冲击问题进行了研究.文献[1]应用Marc软件结合冲击试验，分析了不同形状的Q235B钢材在不同温度时的抗冲击强度规律；文献[2]采用一种新型扩展有限元方法对弹塑性材料的断裂过程和低速冲击损伤进行了研究；文献[3-4]以半潜式起重平台为研究对象，运用有限元软件LS DYNA分析了典型吊物导管架以不同速度、高度、角度跌落时，冲击平台造成的损伤情况；文献[5]以塑料容器为对象，运用LSDYNA程序中的ALE算法研究了容器跌落冲击动力学中液体与固体耦合的问题，从多方面综合分析了冲击应力的影响因素；文献[6-10]对其他物件的跌落冲击领域进行了深入的探索.

文中针对海洋石油平台舱口盖吊装结构，应用LS DYNA软件，分析了某型吊环的极限荷载和断裂状况、单侧吊环脱落时另一侧吊环受到的冲击力以及舱口盖与平台间的冲击响应，并对冲击侧吊环的防破断给出了建议.

1 舱口盖吊装模型

1.1 几何模型的建立

舱口盖吊装结构见图1，仿真所需的部件包括舱口盖、吊链、吊环、锁钩、简易平台5个部分.由于舱口盖和吊链结构比较复杂，且对吊装整体影响较小，因此在建模时进行了必要的简化.对于舱口盖，忽略倒角、连接孔、不规则平面等特征；对于吊链结构，分成几节予以整合.简化后的舱口盖、吊链以及简易平台选择在LS PREPOST中直接进行建模.

图1 舱口盖吊装结构

对于吊环结构，根据尺寸参数，利用SOLIDWORKS软件，建立几何模型；对于锁钩结构，根据计算分析的需要，建立不同尺寸的几何模型，如表1.

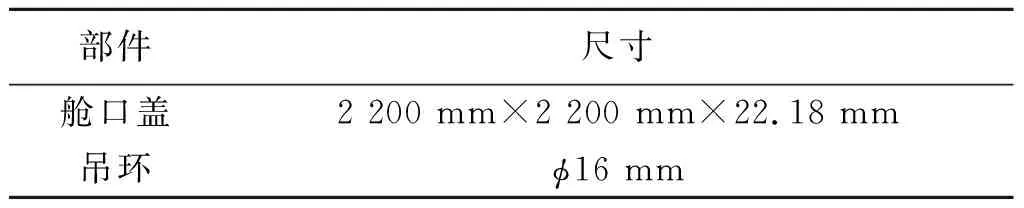
表1 部件尺寸参数

1.2 有限元模型的建立

舱口盖吊装结构采用四六面体单元结合的方式划分，材料选择为Q235钢，有限元仿真模型如图2，材料参数如表2.

图2 舱口盖吊装有限元模型

表2 材料参数

为节省计算时间，四六面体单元的单元列式分别采用10和1；研究吊环受到的作用力时，舱口盖、吊链等非研究对象使用RIGID材料，主要研究对象吊环使用分段线性塑性本构模型；研究舱口盖的冲击响应时，舱口盖和平台使用Johnson-Cook本构模型[11-15].

2 吊环极限荷载分析

2.1 吊环参数

吊环应力分布是由剪切、拉伸、弯曲、扭转组合而成的复杂状态，针对某型Q235钢吊环(图3)，结合不同的失效准则，应用LSDYNA计算其在不同状况下的荷载极限值.

图3 吊环参数(单位：mm)

2.2 锁钩宽度对吊环极限荷载的影响

锁钩的宽度(作用点跨距)会对吊环率先发生破坏的位置及其极限载荷造成影响.当锁钩宽度为10、16 mm时，吊环顶部最先发生断裂，如图4、5.

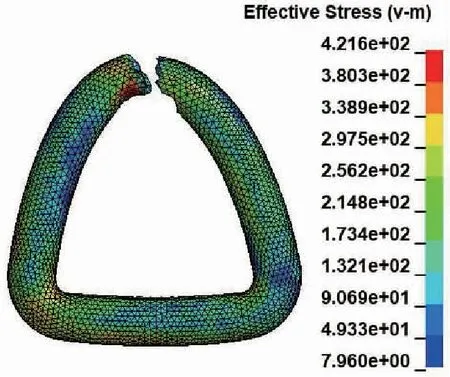
图4 吊环断裂-10 mm宽锁钩

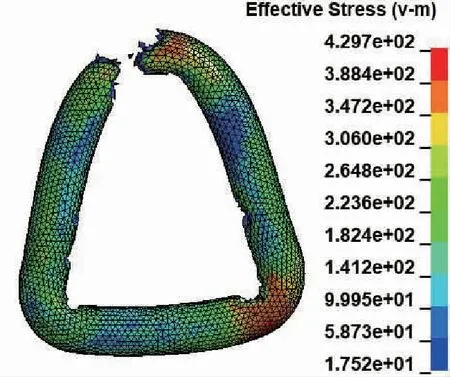
图5 吊环断裂-16 mm宽锁钩

当锁钩宽度为22、32 mm时，吊环底部最先发生断裂，如图6、7.

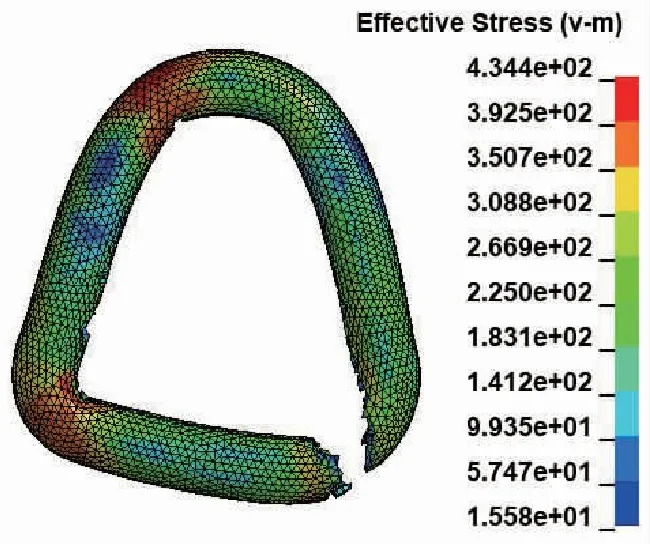
图6 吊环断裂-22 mm宽锁钩

图7 吊环断裂-32 mm宽锁钩

吊环在不同锁钩宽度下的极限载荷值如图8.分析可知：锁钩宽度b越小，吊环变形空间越大，且在一定范围内几乎不影响吊环的极限荷载；但当锁钩宽度过小时，由于吊环顶部最先破坏，吊环断裂时变形减小，极限荷载降低.

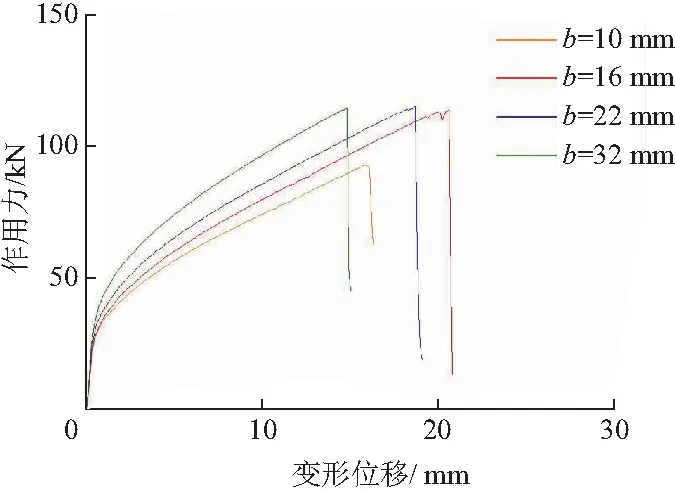
图8 不同锁钩宽下的吊环极限荷载

2.3 应变率对吊环极限荷载的影响

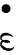
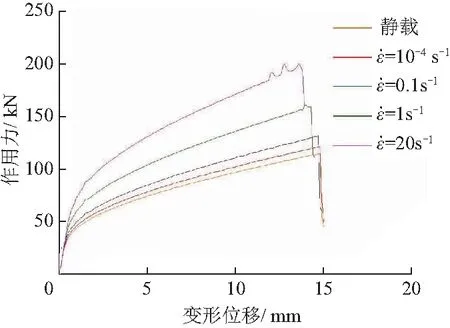
图9 不同应变率下的吊环极限荷载

对比文献[12]可知，计算选用的参数符合Q235钢的材料特性，结果反应出了应变率对吊环极限载荷的影响.此外，环境温度、材料成分、内部组织、截面缺陷等因素对吊环的强度也有很大的影响，文中不作考虑.

3 舱口盖吊装仿真冲击结果分析

3.1 舱口盖对吊环的冲击载荷

基于舱口盖吊装结构分析可知，除舱口盖受到重力作用跌落对吊环的冲击载荷外，跌落过程中舱口盖对锁钩的撞击也会对吊环造成冲击，如图10，这一部分的冲击力大小取决于舱口盖对锁钩作用力方向、锁钩对吊环作用方向的相对性.

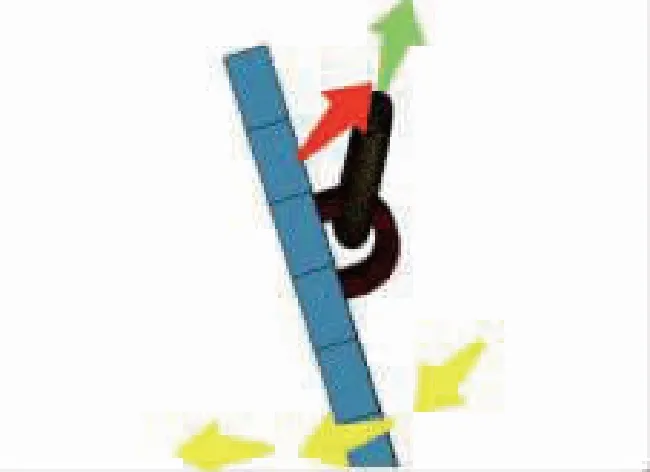
图10 舱口盖、锁钩、吊环相互作用示意图

为探究在舱口盖跌落过程中上述因素对吊环所受冲击载荷的影响，将吊环设置为刚体，模拟计算吊环与锁钩间作用力滤波处理后与吊环极限荷载进行对比.图11为不同吊链长度l、舱口盖与锁钩无撞击情况下吊环与锁钩间的作用力变化历程.

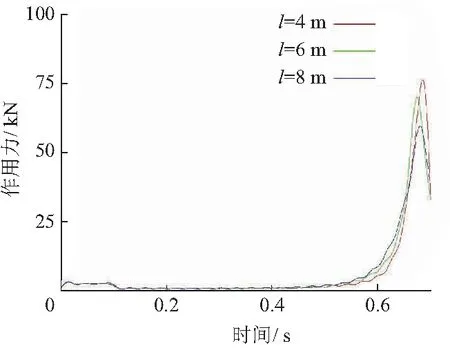
图11 吊链长度对锁钩吊环间作用力的影响

由图可知，吊装平衡后，吊环所受作用力略高于2 500 N；在0.1 s时一侧吊环脱落，舱口盖瞬时偏转，另一侧吊环受到的作用力瞬间减小，而后随着舱口盖的跌落逐渐变大，跌落约0.57 s时达到峰值.显然，吊链越短，舱口盖跌落到最低点转化的重力势能越多；吊链长4 m时，吊环受到的作用力最大值为66 434.8 N，但仍远小于上述吊环的极限荷载.

图12为4 m吊链下舱口盖撞击锁钩与无撞击工况时的作用力对比.在撞击作用下，锁钩与吊环之间的作用力峰值达到了300 kN以上，超出吊环的极限载荷，使得吊环瞬间断裂.

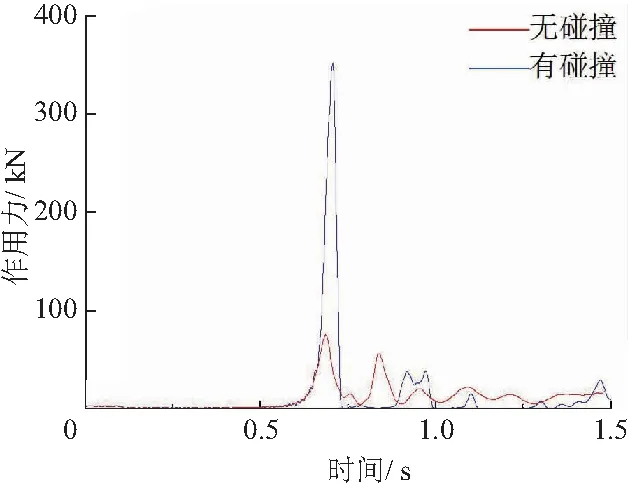
图12 碰撞对锁钩吊环间作用力的影响

仿真结果表明，在特定的冲击位置和方向以及吊环两侧舱口盖作用力臂相差过大的情况下，舱口盖冲击锁钩会使吊环与锁钩间的作用力陡增，这是导致吊环断裂的主要因素.

3.2 舱口盖与平台间的冲击响应

对简易舱口盖以不同倾角、不同速度、不同位置撞击简易平台进行仿真模拟，得到舱口盖与简易平台的应变以及两者间的作用力.以中心为原点，长宽为X、Y轴方向建立坐标系，如图13.

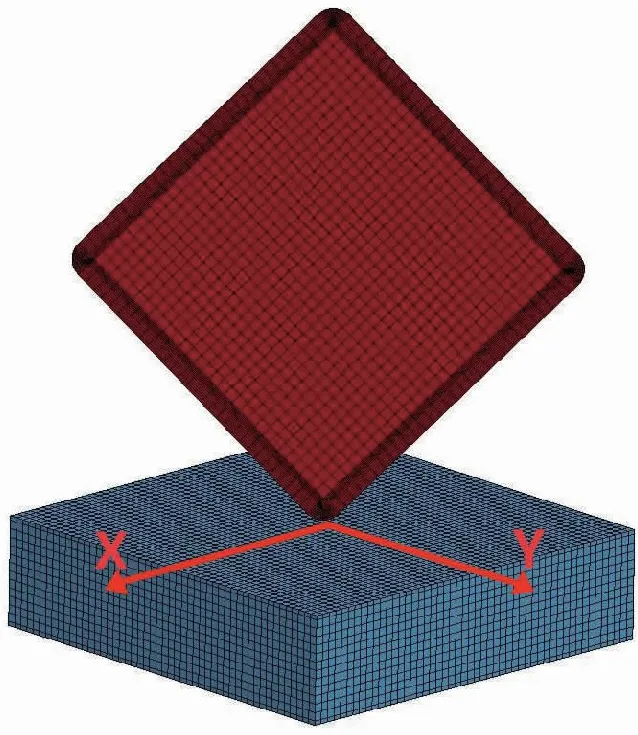
图13 冲击仿真模型

舱口盖因吊环断裂而跌落时，会以较大的速度撞击平台.考虑实际吊装时舱口盖的跌落高度，以速度5 m/s、倾角30°、坐标(0,0)为撞击点作为基本参考，分析速度、角度、位置对冲击的影响.

图14为不同舱口盖倾角α下的冲击力仿真结果.随着倾角增大，作用力峰值快速上升，冲击时间减小；倾角从60°到75°，作用力峰值增加近2倍，使舱口盖撞击处出现较大的应变，达到19%以上，如图15.

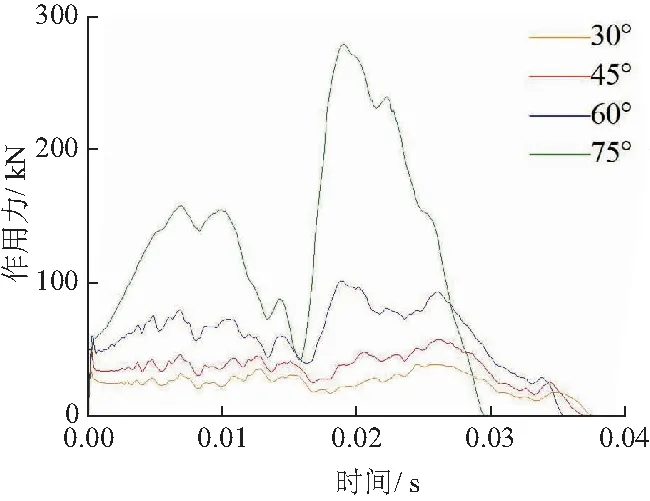
图14 不同倾角下的冲击力

图15 倾角75°的等效应变

图16为舱口盖速度对冲击的影响，随着速度的增大，作用力峰值迅速出现，并与速度v呈线性关系；作用力的变化趋势保持不变，都为增减再增减的历程.速度为10 m/s时，舱口盖最大应变达到33.92%，见图17.

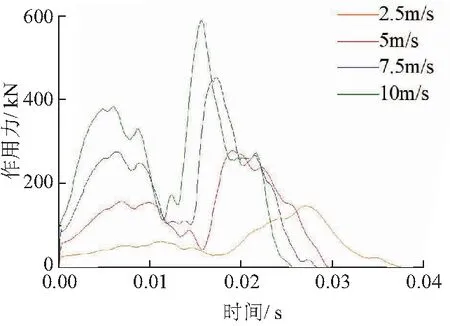
图16 不同速度下的冲击力

图17 速度10 m/s的等效应变

随着舱口盖撞击处向边界靠近，冲击力峰值先减小后增大，冲击时间先增大后减小；作用力趋势变化明显，低谷区逐渐消失，冲击力更快达到峰值，具体的作用力变化和对比见图18、19.

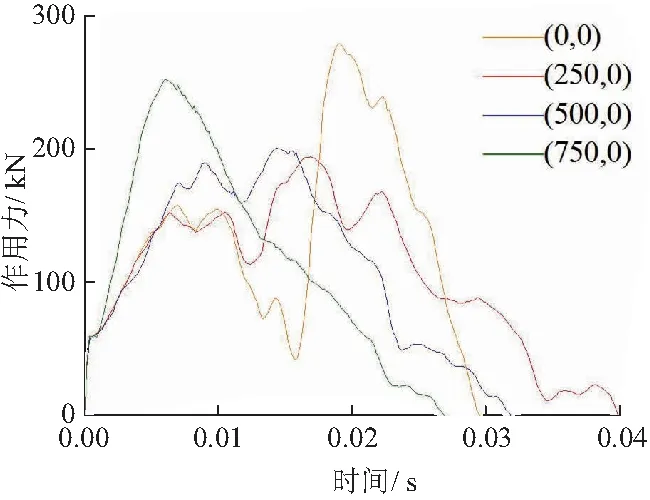
图18 沿X轴不同位置的冲击力

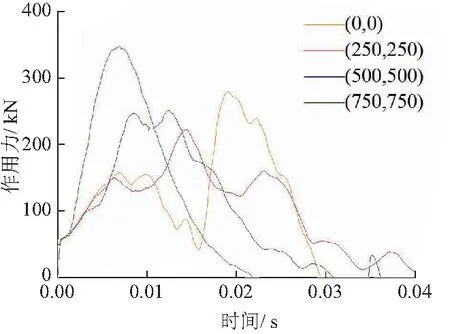
图19 沿X、Y方向不同位置的冲击力

4 结论

(1) 吊环的荷载极限随应变率的增大而增大；吊环的断裂位置通常在其底部，但锁钩宽度过小，如10 mm时，吊环在顶部发生断裂并且极限载荷降为约90 000 N.

(2) 舱口盖吊装过程中一侧吊环脱落时，舱口盖对另一侧吊环造成冲击载荷与吊链长度有关，吊链较短时冲击力结果较大；舱口盖与锁钩相互作用的位置和方向是影响吊环断裂的主要因素，因此适配吊环的锁钩能够有效避免该情形下的吊环断裂.

(3) 舱口盖跌落时与平台的冲击力峰值随其速度和倾角的增大而增大，同时受到撞击位置的影响.