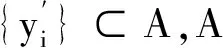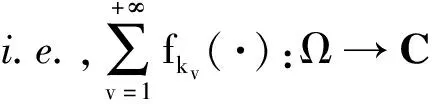λ-乘数收敛不变性的判据*
2021-03-04邢志勇蔡俊娟
邢志勇,蔡俊娟,黄 丽
(1.厦门海洋职业技术学院公共教育学院,福建 厦门 361100;2.太原科技大学应用科学学院,山西 太原 030024)
扩大已知乘数收敛不变性的不变范围乃至求得最大不变范围是有重要意义的,前辈在这方面作了不懈努力并取得了一定的成果,这类工作今后还要继续做下去.泛函分析空间理论[1-8]特别是局部凸空间理论也应发展到一个新的理论水平,这其中就包括乘数收敛不变性的理论研究.例如,Orlicz-Pettis定理[9]指出子级数收敛是乘数收敛不变性,Mackey定理[10]认为有界性是乘数收敛不变性,Mazur定理[11]断定凸集的闭包是乘数收敛不变性.此外,还有学者给出了特殊情形下的乘数收敛不变性.例如,Schur引理[12]指出(l1,l∞)中序列的收敛是乘数收敛不变性,Diestel-Faires定理[13]指出Banach空间X使(X′,‖·‖)不含l∞时的X′中级数的子级数收敛对(X′,X)而言不仅是乘数收敛不变性,还是全程不变性,即(X′,X)-极拓扑全体上的不变性.笔者拟在特定空间研究λ-乘数收敛不变性,通过讨论算子级数赋值收敛的不变范围获得赋值收敛的重要意义.
1 预备知识
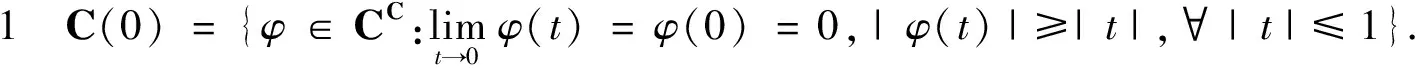
X,Y是拓扑线性空间(Topological Vector Space,简称TVS)[2,14].对于∀φ∈C(0),U∈N(X),令
Rφ,U(X,Y)={f∈YX:∀x∈U,|t|≤1,∃s∈[0,|φ(t)|],使得f(tx)=sf(x)}.
若X,Y是线性空间,φ∈C(0),则有
Rφ(X,Y)={f∈YX:∀x∈X,|t|≤1,∃s∈[0,|φ(t)|],使得f(tx)=sf(x)}.
定义2[2,15]X是线性空间,λ(X)⊂XN.若对于∀(xj)∈λ(X),∃(tj)∈c0,(zj)∈λ(X),使得xj=tjzj,∀j∈N,则称λ(X)是c0-分解的;若当(xj)∈λ(X),(tj)∈c0时,有(tjxj)∈λ(X),则称λ(X)是c0-合成的.
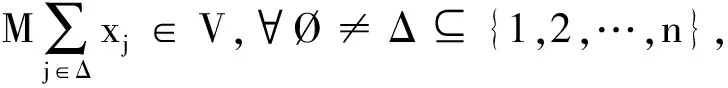
定义3[15]λ(X)⊂XN.若当(tj)∈l∞,(xj)∈λ(X)时,有(tjxj)∈λ(X),则称λ(X)是l∞-合成的;若λ(X)是c0-分解的和c0-合成的,则称λ(X)是l∞-合成的.
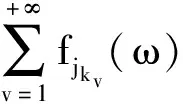
2 主要结果及其证明
定理1X,Y是线性空间,φ,ψ∈C(0),λ(X)⊂XN.若λ(X)是c0-分解的和c0-合成的,则对于∀{fj}⊂Rφ(X,Y),Yψ⊂Rψ(Y,C),下列2个条件等价:


证明(ⅰ)⟹(ⅱ).

取(tj)∈c0,(zj)∈λ(X),使得(xj)=(tjzj).因为
φ(δk)→0,
所以不妨设δk<1,|φ(δk)|<1,∀k∈N.对于每个mk≤j≤nk,存在0≤θj≤|φ(δk)|<1,0≤sj≤|ψ(θj)|,使得

(1)
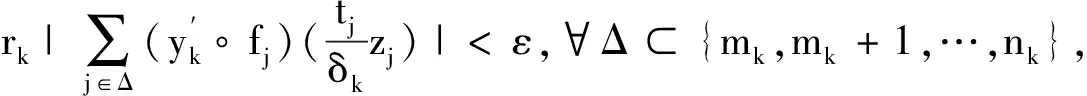

maxΔk (2) 从而每个fk:Ω→C连续. 又对N中的列k1 由定义3可知,因λ(X)是l∞-合成的,(uj)∈λ(X),故由条件(ⅰ),∃y∈Y,使得 于是 (ⅱ)⟹(ⅰ)同理用逻辑反证法可证.证毕.