基于混合效应的湖南马尾松次生林单木生长模型

陈哲夫，肖化顺，龙时胜

（1.湖南文理学院 资源环境与旅游学院，湖南 常德 415000；2.中南林业科技大学 林学院，湖南 长沙 410004）

马尾松Pinus massoniana分布极广，产于秦岭、淮河流域以南，东起沿海低山丘陵，西至川西大相岭东坡，南达华南南部，遍布于华中、华南，是我国南方集体林区经营历史悠久、最喜闻乐见的树种之一，在我国国民经济发展、国土生态安全和应对全球气候变化等方面发挥着特别重要的作用。根据第七、八、九次全国森林资源连续清查结果，我国马尾松林面积占比均在4.5%以上，蓄积占比均在3.5%以上，在所有优势树种中面积与蓄积占比均处于前列[1]。

我国有关马尾松生长模型的研究主要集中在人工林[2-3]，包括林分优势高[4]和自稀疏[5]模型等，关于马尾松天然林的研究则相对较少，主要包括材积、胸径[6]和树高[7]等生长模型的研究。单木生长模型是林分生长模型的基础，建立林木的单木生长模型，不仅对预测林木个体的生长过程具有重要意义，还可为林分整体的经营管理提供经营决策方案，从而提升森林的经营水平[8-11]。传统的建模方法虽然能够取得一定的预测精度，但未能考虑立地之间的差异，导致其存在一定的局限性，而含有随机参数的建模方法则可以很好地解决这一问题，其相比传统应用最小二乘法的建模方法取得了较高的预测精度[12-14]。近年来，混合效应模型已广泛应用于林业中[15-16]，包括改进Gompertz 模型对栓皮栎树高与胸径的研究[17]，以及对华北落叶松单木冠幅[18]和树高模型[19]的研究等，均取得了一定的成果，提升了模型的预测精度。本研究以湖南省马尾松次生林为研究对象，建立其单木断面积和材积的基础生长模型，在此基础上加入随机参数，构建基于样地水平的湖南马尾松次生林单木断面积和材积生长模型，以期准确预估该林分的生长过程，为其生长预测和可持续经营提供技术指导。

1 研究区概况

湖南省位于我国中南部，长江中游，地处108°47′～114°15′E，24°38′～30°08′N，土地总面积2 118 万hm2，其中林地面积为1 300 万hm2，森林覆盖率为59.57%，活立木蓄积5.05 亿m3[1]。海拔24～2 122 m，地貌以800 m 以下的低山和丘陵为主，气候为典型的大陆性亚热带季风湿润气候，年均气温15～18oC，年日照数1 300～1 800 h，年降水量1 200～1 700 mm，土壤呈垂直性地带性分布，主要为红壤和黄壤。主要的乔木树种有马尾松、青冈栎Cyclobalanopsis glauca、杉木Cunninghamia lanceolata、樟树Cinnamomumbodinieri、枫香Liquidambar formosana和木荷Schima superba等，主要的灌木树种包括厚皮香Ternstroemia gymnanthera、山茶Camellia japonica、鹿角杜鹃Rhododendron latoucheae和细枝柃Eurya loquaiana等，主要的草本植物为兰花Cymbidium、麦冬Ophiopogon japonicus、芒萁Dicranopteris pedata和蕨Pteridium aquilinumvar.latiusculum等。

2 材料与方法

2.1 数据来源

以湖南省第八次国家森林资源连续清查样地数据为基础数据，选取20 块林分起源为天然林、树种组成中马尾松占比80%以上且林分郁闭在0.6以上的马尾松次生林，样地分布于湖南省9 个地（市、州）区，包括张家界、岳阳、常德、郴州、娄底、邵阳、衡阳、永州市和湘西土家族苗族自治州，能够代表湖南省马尾松次生林的整体生长情况。

马尾松样地为0.066 7 hm2的方形样地，立地因子包括海拔、坡度、坡位、坡向、土壤类型、土层厚度、腐殖质厚度和枯枝落叶厚度等，林分因子包括树种、郁闭度、胸径（D）、优势高（H）及其它衍生数据等，此外，还以龙时胜等[20]基于林木多期测定数据的异龄林年龄估计方法计算出样地内每株林木的年龄（A）。

对各样地概况进行统计（表1），其中海拔范围为80～510 m，平均年龄为18～31 a，平均胸径为8.4～15.3 cm，样地内的主要乔木树种除马尾松外，还包括栎类、樟木、杉木、枫香和泡桐Paulownia等。

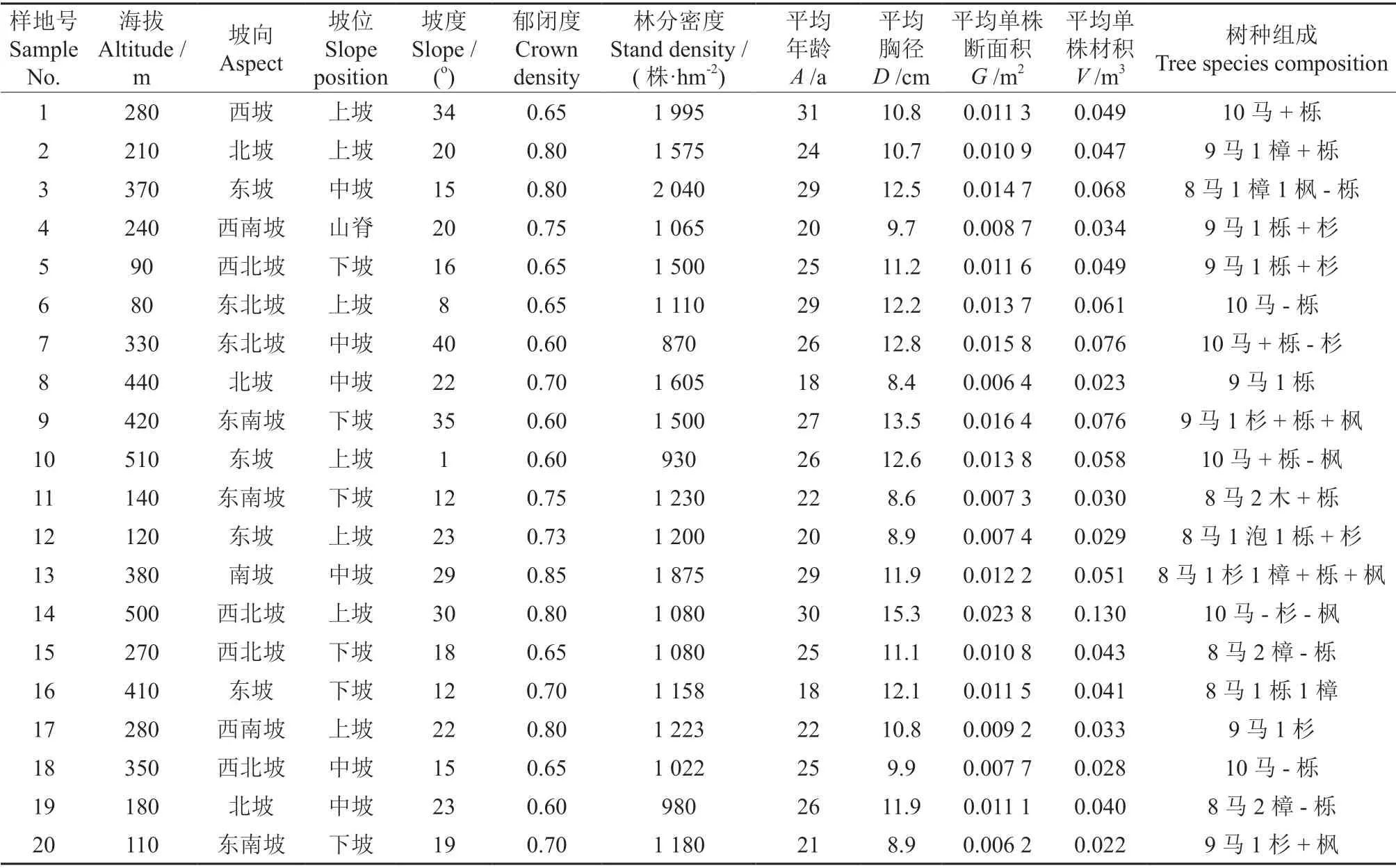
表1 样地概况Table 1 The basic facts of sample plots

筛选出所有样地中的马尾松共993 株，以随机抽样的方法选取总样本的2/3 作为建模数据，剩余1/3 的数据作为检验样本，分别对建模样本和检验样本的各林分变量进行特征统计（表2）。其中建模样本的年龄变化为7～81 a，平均值为26 a；胸径变化范围为5.0～32.2 cm，平均值为12.6 cm；单木断面积（Basal area，G）变化范围为0.002 0～0.081 4 m2，平均值为0.014 5 m2；单株材积（Volume，V）变化范围为0.004～0.548 m3，平均值为0.065 m3。检验样本的年龄变化为7～103a，平均值为26 a；胸径变化范围为5.1～30.4 cm，平均值为12.3 cm；单木断面积变化范围为0.002 0～0.072 6 m2，平均值为0.014 0 m2；单株材积变化范围为0.005～0.472 m3，平均值为0.065 m3。

表2 建模数据与检验数据特征统计Table 2 Characteristic statistics of modeling data and testing data

2.2 单木生长模型的选择

选择5 个具有生物学意义的理论方程，分别构建湖南马尾松次生林单木断面积和材积生长的基础模型，各模型及其表达式见表3，模型的拟合及参数计算在林业统计软件Forstat 2.0 中的非线性回归模块中进行。

2.3 混合效应模型的构建

在建立固定效应模型的基础上，考虑不同样地间的差异对马尾松林木断面积、材积生长的影响，构建基于样地水平的混合效应模型，其模型的一般表达形式如下：

表3 基础模型与表达式†Table 3 The basic model and expression

式（1）中：Gij、Vij、Aij分别为第i块样地第j株林木的断面积、材积和年龄；f(ijφ,Aij)为描述断面积-年龄、材积-年龄关系的函数；ijφ为r×1 维的形参向量（r为形参个数）；β为p×1 维的固定效应向量（p为固定参数个数）；εij为随机误差项；μi是服从期望为0、方差-协方差矩阵为Ψi(q×1)的独立随机效应向量，且假定μi与εij间相互独立（q为模型随机参数个数）；Pij和Qij分别为对应向量的设计矩阵；Rij为样地内误差效应的方差-协方差结构矩阵。

构建混合效应模型，通常需要考虑以下三个方面的问题：

1）参数效应的确定

混合效应模型的参数包括固定效应参数和随机效应参数，本研究将所有可能的随机参数组合加入到模型中进行混合效应模拟，不同随机参数的混合效应模型拟合效果对比采用赤池信息准则（AIC）和贝叶斯信息准则（BIC），AIC 和BIC 值越小表示模拟效果越好，对于不同参数个数的模拟过程，还要进行似然比检验（LRT），当P＜0.000 1 时，代表二者之间差异显著，当二者之间差异不显著时，选择参数更少的模拟以避免参数过多化的现象。

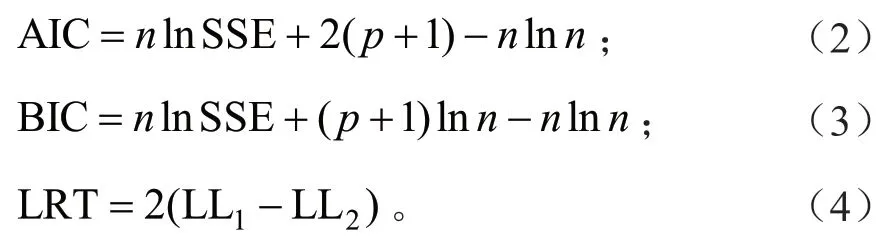
式（2）～（4）中：n为样本数；p为参数个数；LL1和LL2分别为2 个对比模型的极大似然值。

2）确定样地内方差-协方差结构（Rij）

样地内方差-协方差结构能够反映误差异方差和自相关问题，本文中所获取的研究数据为非连续性测量数据，因此在时间上不存在自相关，因而采用常用的误差效应方差-协方差结构来描述：

式中：σ2为模型的误差方差；In为描述样地内误差的n×n维方差矩阵。

3）随机效应的方差-协方差结构的确定（D）

随机效应的方差-协方差结构矩阵可以反映不同样地内马尾松断面积和材积与年龄之间关系的差异性，其结构会根据随机参数个数的变化而变化，本研究以广义正定矩阵来描述随机效应的方差-协方差结构，以包含3 个随机参数的方差-协方差结构矩阵为例，其结构如式（6）。

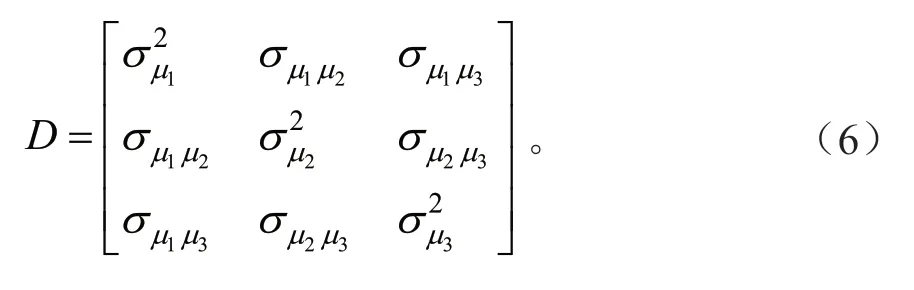
2.4 模型评价指标的选取

基础模型的选取指标为确定系数（R2）、预估精度（P）和残差平方和（SSE），其中R2和P越大，SSE 越小，模型的拟合效果越好；对于基础模型与混合效应模型的拟合效果对比，采用确定系数、平均误差（Bias）和均方根误差（RMSE）等指标来评价，其中R2越大，Bias 和RMSE 越小，说明模型拟合效果越好。

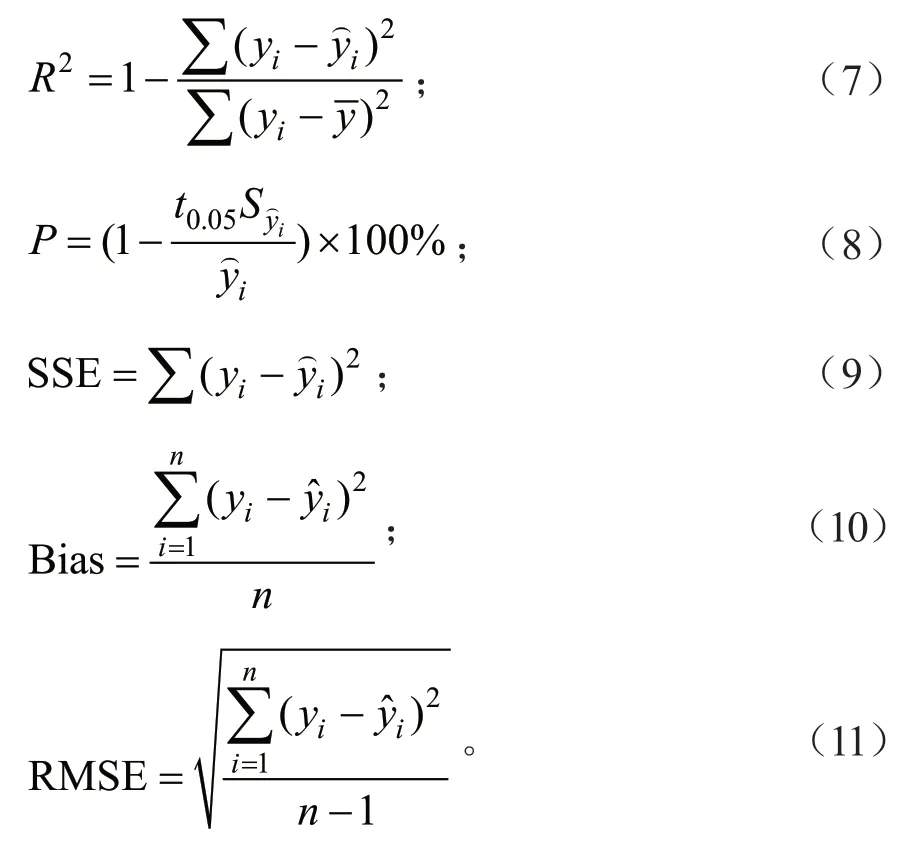
式（7）～（11）中：yi为实际值；为预测值；为平均预估值；t0.05为置信水平a=0.05 时的t分布值；n为样本数。

3 结果与分析

3.1 基础生长模型的选择

马尾松单木断面积基础模型的拟合结果见表4。由表4可以看出，5 个模型除模型1 的拟合效果较差（R2=0.639，P=87.16%，SSE=0.036）外，其余4 个模型的拟合效果尚可，其确定系数均在0.73 以上，拟合精度也在96.5%以上，选择其中拟合效果最佳的模型2（Logistic 模型）作为断面积生长的基础模型（R2=0.746，P=98.13%，SSE=0.025）；同理，将马尾松单木材积生长模型确定为模型4（Richards 模型），其确定系数（R2=0.703）和预测精度（P=97.20）均为5 个模型中最大，其残差平方和（SSE =1.034）为最小（表5）。湖南马尾松次生林单木断面积和材积基础模型如式（12）～（13）：

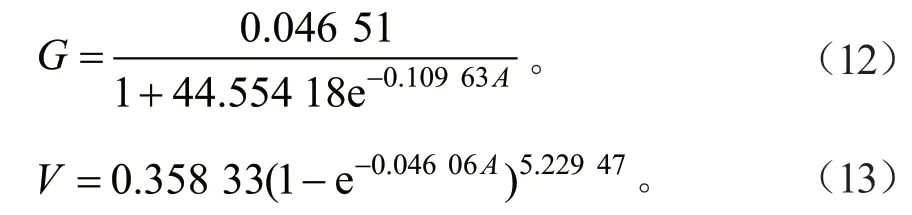
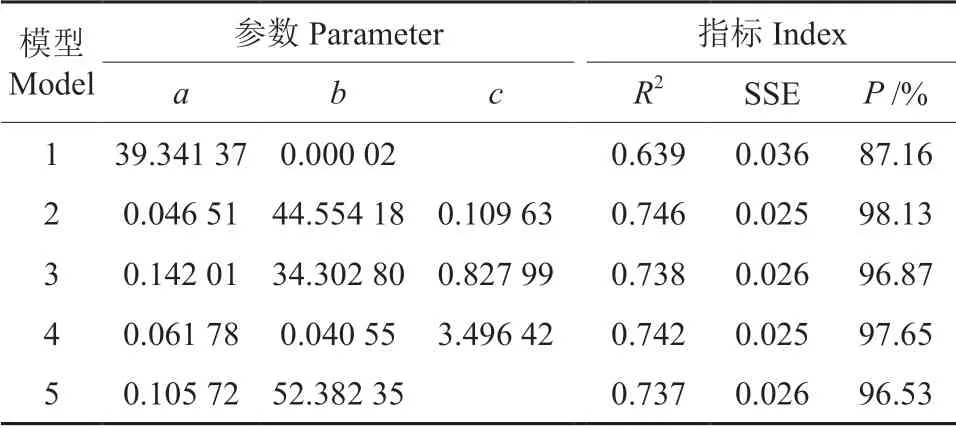
表4 断面积生长方程拟合结果Table 4 Fitting results of basal area growth equation

表5 材积生长方程拟合结果Table 5 Fitting results of volume growth equation

3.2 断面积和材积生长特征分析

根据所得到的断面积生长方程，可绘制出湖南马尾松次生林单木断面积总生长量曲线，再根据总生长量计算出断面积的平均生长量和连年生长量，并绘制二者之间的变化规律曲线（图1）。由图1可以看出，断面积在0～20 a 生长较为缓慢，在21～50 a 生长速度较快，51 a 以后生长趋于平稳，在90 a 时生长已基本停止，此时的断面积达到最大值（0.046 4 m2）；断面积连年生长量在35 a时达到最大值，为0.001 25 m2/a，随后逐渐减小，在90 a 时其值趋近于0；平均生长量在50 a 时达到最大，为0.000 78 m2/a，此时的断面积平均生长量与连年生长量相等，随后断面积平均生长量逐渐减小，其值也一直大于连年生长量。

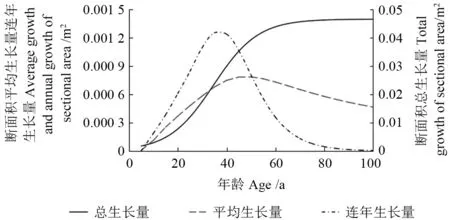
图1 断面积生长特征曲线Fig.1 Growth characteristic curve of basal area

同理，对材积生长特性进行分析，发现材积在0～60 a 均有较快的生长速度，61 a 以后生长速度减缓，生长趋于平稳，在150 a 时生长已基本停止，此时的材积达到最大值0.356 5 m3；材积连年生长量在40 a 时达到最大值（0.00 669 m3/a），随后逐渐减小，在150 a 时其值趋近于0；平均生长量在65 a 时达到最大，为0.004 25 m3/a，此时的材积平均生长量与连年生长量相等，随后材积平均生长量逐渐减小。

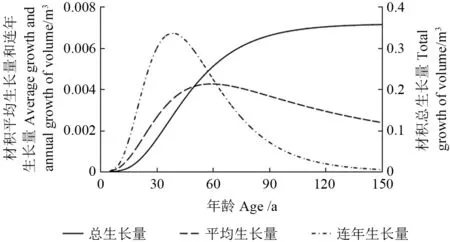
图2 材积生长特征曲线Fig.2 Growth characteristic curve of volume

3.3 基于混合效应的单木生长模型

在确定基础模型的前提下，加入含样地效应的随机参数，构建基于混合效应的湖南马尾松次生林单木断面积和材积生长模型。首先，在式（12）中加入所有可能的随机参数组合，发现共有6 种收敛的模拟过程，拟合结果（表6）显示，所有含随机参数的模拟其拟合效果均优于基础模型（AIC=-5 417.850，BIC=-5 401.364），含1 个随机参数的模拟共有3 种收敛的情况，其中模拟4（AIC=-5 680.460，BIC=-5 658.007）的结果优于模拟2 和模拟3，含2 个随机参数的拟合有2 种收敛的结果，模拟5（AIC=-6 348.868，BIC=-6 317.433）的效果优于模拟6，含3个随机参数的模拟仅有一种结果模拟7（AIC=-6 458.433，BIC=-6 413.526）。对于含不同随机参数个数的模拟过程进行似然比检验，发现模拟5 的结果显著优于模拟4（LRT=672.408，P＜0.0 001），而模拟7 的结果显著优于模拟5（LRT=115.566，P＜0.000 1），最终将含随机参数μ1、μ2、μ3的混合效应模型作为最优模型。同理，材积的随机参数模拟结果显示模拟6（AIC=-4 211.681，BIC=-4 166.774）的拟合效果最佳（表7），将其随机参数确定为μ1、μ2、μ3，因此，基于混合效应的湖南马尾松次生林单木断面积和材积生长模型一般表达式为：

式（14）～（15）中：μ1、μ2、μ3为样地水平的随机效应参数。

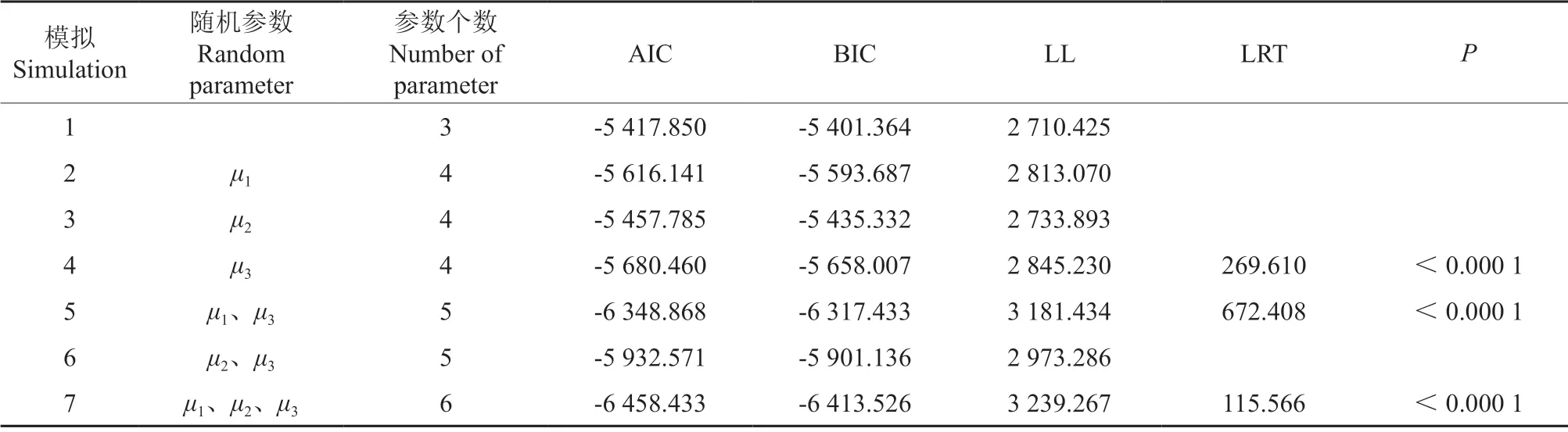
表6 断面积混合效应模型拟合结果比较Table 6 Comparison of fitting results of basal area mixed effect model

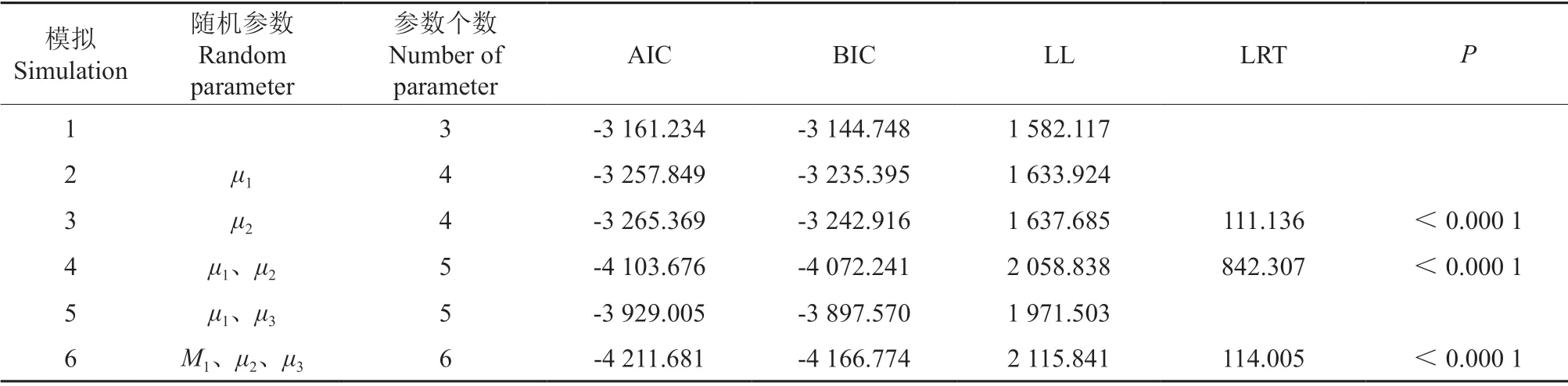
表7 材积混合效应模型拟合结果比较Table 7 Comparison of fitting results of basal area mixed effect model

3.4 模型评价分析

通常对比基础模型与混合效应模型的残差分布可以直观地判断模型拟合效果的差异及误差的异方差性（图3）。为确定所拟合的模型是否存在异方差，分别绘制了马尾松断面积、材积生长基础模型与混合效应模型的残差分布（图3～4）。结果（图3～4）显示，基础模型的残差分布范围大（图3A，图4A），分布不均匀，随着预测值的逐渐增大，其残差值也随之增大，存在一定的异方差；而混合效应模型的残差分布范围明显减小（图3B，图4B），且分布较为均匀，没有出现明显的不规则形状（如哑铃型、喇叭形和抛物线形等），表明混合效应模型的异方差已基本消除。

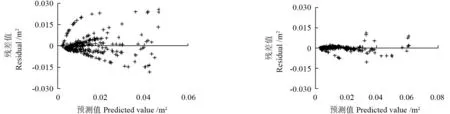
图3 断面积残差分布Fig.3 Residual plots of basal area

图4 材积残差分布Fig.4 Residual plots of volume

对马尾松断面积和材积生长的基础模型与混合效应模型进行参数估计与模型评价，各模型的参数估计值与方差组成见表8。各模型的拟合统计指标结果显示，混合效应模型的AIC、BIC、平均误差（Bias）和均方根误差（RMSE）值均小于基础模型，在数量上，模型14 的Bias 值由模型12 的0.000 26 降低到0.000 01，其RMSE 值由0.006 40降低到0.001 95，模型15 的该两项指标也较模型13 有显著降低，分别从0.001 73 降低到0.000 13、由0.038 20 降低到0.000 20；混合效应模型的确定系数（R2）相比基础模型有很大的提升，其中模型14 的R2较模型12 提升了36.2%，模型15 的R2较模型13 提升了37.0%，相比基础模型，混合效应模型的预测精度（P）也有一定的提升，分别提升了1.84%和2.67%。综上所述，含以样地为随机效应的混合效应模型拟合效果优于基础生长模型，能够更好地预测马尾松的生长过程。

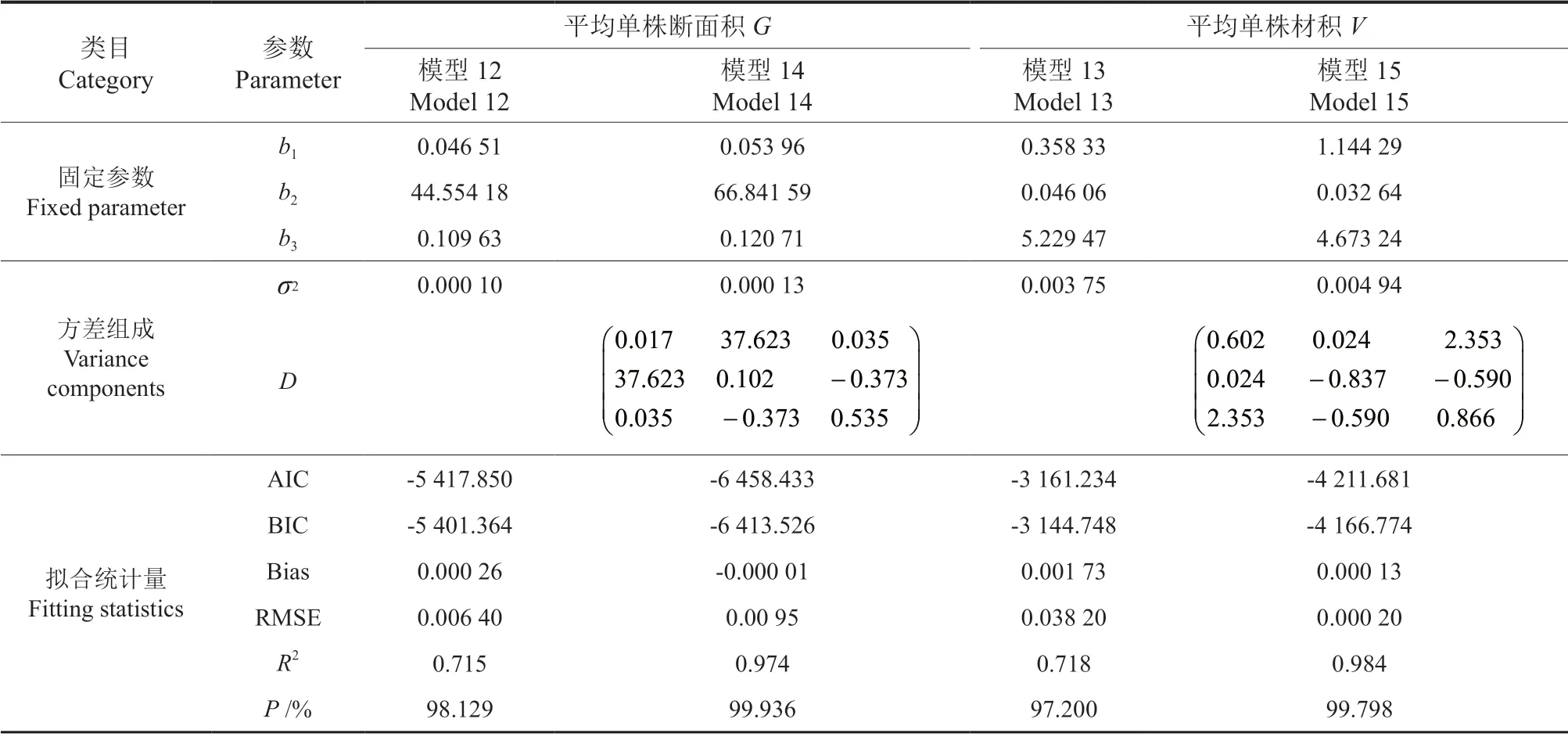
表8 基础模型与混合效应模型拟合效果对比Table 8 Fitting result of basic model and mixed effect model

4 结论与讨论

本研究分别以马尾松单木断面积和材积为因变量，构建其关于年龄的生长模型，在5 个基础模型中Logistic 方程能够最好地反映断面积的生长规律，该模型有最大的预测精度（P=98.13%）和确定系数（R2=0.746），同时其残差平方和（SSE=0.025）最小；而材积生长的最优基础模型为Richards 方程，其R2和P最大（0.703，97.20%），SSE 最小（1.034）。在此基础上，构建了基于样地水平的混合效应模型，以期消除立地间的差异，对不同随机参数的混合效应模型进行模拟，对比不同随机效应模型的赤池信息准则（AIC）、贝叶斯信息准则（BIC），对不同随机参数个数的模拟进行似然比检验（LRT），以避免参数过多化的现象，发现断面积和材积生长的混合效应模型其随机参数均为μ1、μ2、μ3，其拟合效果均显著优于其他模型过程（P＜0.000 1）。相比基础模型，混合效应模型的拟合效果明显更优，其平均误差（0.000 01，0.000 13）和均方根误差（0.001 95，0.000 20）显著降低，确定系数（0.974，0.984）大幅提升，预测精度（99.936%，99.798%）也有所提高。混合效应模型有更好的拟合效果，能够更精确地预测马尾松次生林的生长规律，为其提供更有效的经营措施。

本研究的研究数据来自湖南省9 个地区，具有很强的代表性，其所构建的生长模型能够很好地反映湖南马尾松次生林的整体生长规律，所形成的生长预测方程也能够广泛应用于湖南省各地区。研究结果与前人构建的哑变量模型[21]和混合效应模型[22-23]所得到的结果相似，均提示了模型的预测精度，具有更强的适用性。通常，单木生长与年龄、立地质量和林分密度（或竞争因子）密切相关，本研究选取林分密度相似的马尾松次生林样地，以年龄为自变量、样地为随机效应构建单木生长模型，但未考虑到林木之间的竞争关系，为研究中存在的不足之处，今后将在建模过程中加入林木竞争因子，以期更加精确地反映林木的生长规律。