大直径高温熔盐储罐罐顶接管的强度及 罐体稳定性分析

徐卫兵，赵 伟，王 晓，周 治，段杨龙，张俊峰

(1. 中国电建集团西北勘测设计研究院有限公司，西安 710065；2. 太阳能利用工程技术研究所，西安 710065)

0 引言

随着可再生能源技术的大力发展与应用，太阳能作为一种清洁、无污染、取之不尽的可再生能源得到越来越广泛的应用，而太阳能热发电就是其中一种重要的太阳能利用方式。在塔式熔盐太阳能热发电站中，熔盐储罐是其核心设备之一，储罐设计的好坏关系着塔式熔盐太阳能热发电站能否正常运行[1-4]。若熔盐储罐设计不合理，会引起熔盐泄漏，将导致太阳能热发电站长期停运。

目前投运、建设和设计的塔式熔盐太阳能热发电站均采用非直接储热方式——双罐储热[5-7]。该方式是在高温熔盐储罐罐顶安装长轴熔盐泵[8]，熔盐泵与高温熔盐管道连接，熔盐管道的热应力通过熔盐泵对罐顶接管产生力的作用，从而会影响储罐罐顶的稳定性。然而，目前针对储罐罐顶接管的强度及罐体稳定性的研究较少[8]。为保证储罐的长期、安全、稳定地运行，本文通过对高温熔盐储罐(储热罐)罐顶接管进行建模计算，分析熔盐储罐罐顶接管荷载对储罐结构强度和罐体稳定性的影响，从而为今后大直径高温熔盐储罐的设计和施工提供有力依据。

1 储罐结构及材料参数

本文以青海省某塔式太阳能热发电站中的熔盐储罐(储热罐)为例进行分析。该储罐主要由罐顶、罐壁、罐底及保温层组成。其主要结构参数为：罐壁的中径为φ25.03 m，罐壁的总高度为12.5 m；罐底中幅板的厚度为11 mm，过渡板的厚度为16 mm，边缘板的厚度为22 mm；罐顶的拱顶半径为30036 mm，拱顶高度为2862 mm，罐顶中心板的厚度为10 mm，中间板的厚度为15 mm，边缘板的厚度为18 mm，且罐顶布置有环向和径向加强筋；罐体保温层的厚度为400 mm。该熔盐储罐罐体的结构示意图如图1 所示。图中，i为底板的坡度。

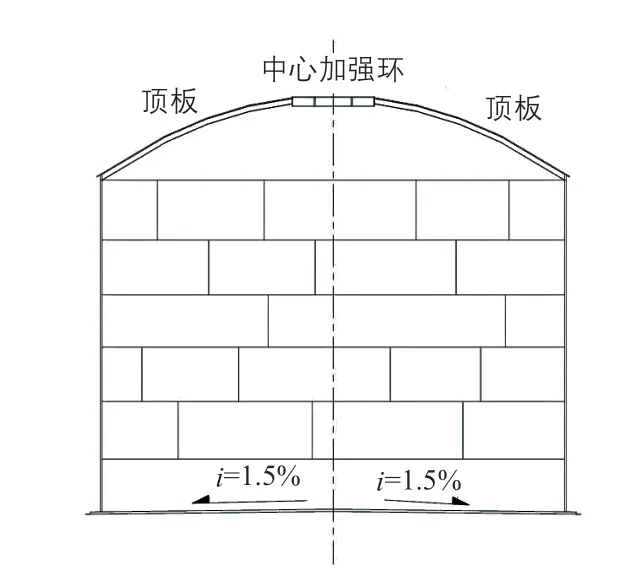
图1 熔盐储罐罐体的结构示意图Fig. 1 Structure schematic diagram of molten salt storage tank

罐壁、罐底板和罐顶材料均选用TP347H，查阅《压力容器》、《压力容器材料实用手册》，这种材料的各参数如表1所示。

表1 TP347H材料参数Table 1 Parameters of TP347H material

2 有限元模型的建立

采用 ANSYS软件SHELL 181单元建立罐体(罐顶和罐壁)整体的有限元模型，如图2a所示；利用Beam189梁单元建立罐顶的径向与环向加强筋模型，如图2b所示。

图2 储罐罐体整体结构与罐顶加强筋结构模型Fig. 2 Geometric model of overall structure of storage tank body and rib structure of storage tank top

在本有限元计算模型中，主要从两方面来保证网格质量：一方面是采用四边形单元进行网格划分，另一方面是绘制不同单元数量下的罐体整体结构(不涉及接管)的等效位移曲线。图3为网格质量对计算结果的影响，由图可知，单元数量在6万个以上时，最大等效位移曲线趋于平缓，因此，单元数量选取6～8万个较为合适。通过赋予相应的材料参数进行网格划分，共得到62564个单元和62799个节点。

图3 网格质量对计算结果的影响Fig. 3 Effect of grid quality on calculation results

3 储罐罐顶接管的荷载分析

熔盐储罐罐顶的3个接管位置的管道入口分别为溢流入口(N04)、热泵再循环入口(N05)和热熔盐入口(N10)，如图4所示。相应地选取N04′、N05′和N10′作为3个管口中心的节点，在节点位置分别施加X、Y、Z方向的集中力FX、FY和FZ；同时在N04′、N05′和N10′节点附近位置建立节点集，再施加X、Y、Z方向的扭矩MX、MY和MZ。储罐罐顶3个接管位置的管道入口处的最大受力和最大扭矩情况如表2所示。

图4 储罐罐顶的3个接管位置的管道入口Fig. 4 Pipe inlet of theree nozzle locations on storage tank top

表2 储罐罐顶3个接管位置的管道入口处的最大受力和最大扭矩情况Table 2 Maximum force and torque at pipe inlet of three nozzle locations on storage tank top

4 罐顶接管荷载的强度分析

4.1 罐顶接管荷载对罐体强度的影响分析

对罐顶接管荷载对罐体强度的影响进行分析。在塔式熔盐太阳能热发电站运行时，罐体承受的荷载包括熔盐静压(熔盐高度为11.5 m)、罐体和保温层自重，以及罐顶接管的集中力和扭矩。罐体在全部荷载作用下的等效位移云图和von Mises 等效应力云图如图5所示。

由图5可知，罐体在全部荷载作用下的最大等效位移值为11.14 mm，位于N10接管的位置；最大von Mises等效应力值为93.54 MPa，同样位于N10接管的位置，这是由于N10接管位置受到的接管外荷载最大所致。同时从图中还可以看出，最大von Mises等效应力仅存在于局部区域，且最大von Mises等效应力值小于TP347H材料在580 ℃时的屈服应力112 MPa，这表明罐体的结构在该荷载条件下仍处于弹性受力状态，罐体的整体结构强度符合要求。

图5 罐体在全部荷载作用下的等效位移和von Mises 等效应力云图Fig. 5 Cloud diagram of equivalent displacement and von Mises equivalent stress of tank body under all loads

4.2 接管局部结构的强度分析

为进一步分析接管具体部位对罐顶局部强度的影响，建立了接管的局部模型进行有限元计算。考虑到N04接管和N05接管的规格为φ89 mm×7.62 mm，直径较小；而且根据图5可知，N04接管和N05接管的最大等效位移、最大von Mises等效应力均非常小，因此本小节内容不对N04接管和N05接管的局部结构强度进行讨论，仅对N10接管的局部结构强度进行有限元计算。N10接管局部结构的有限元模型如图6所示。

图6 N10接管局部结构的有限元模型Fig. 6 Finite element model of local structure of N10 nozzle

约束罐顶板周边所有自由度后，在N10接管最上端施加表2中N10接管对应的所有荷载，并建立线弹性材料模型。N10接管局部结构的等效位移和von Mises 等效应力云图如图7所示。

“书记给我们开会，我知道你们返30%～40%的回扣，但是你们要给我做好，就是不要去被曝光，就是有查的时候要隐蔽，然后打钱不能让客人知道。”○13梁经理，德吉梅朵风情街。

图7 N10接管局部结构的等效位移和von Mises 等效应力云图Fig. 7 Cloud diagram of equivalent displacement and von Mises equivalent stress of local structure of N10 nozzle

由图7可知，N10接管局部结构的最大等效位移为13.39 mm，位于接管的顶部，导致接管向罐顶外侧偏移；最大von Mises等效应力为125.16 MPa，该值大于TP347H材料在580 ℃时的屈服应力112 MPa；最大von Mises等效应力发生在接管与罐顶连接处，主要是由于此位置存在结构不连续的情况，从而产生过大的集中应力和局部应力，导致接管与罐顶连接位置处于不安定状态，而这易引起接管局部结构的热疲劳失效。

下文分别通过增设筋板和补强圈的方式来验证提高N10接管局部结构的承载性能的可能性。

4.2.1 增设筋板的影响分析

图8为增设筋板后N10接管的局部结构示意图。

图8 增设筋板后N10接管的局部结构示意图Fig. 8 Local structure schematic diagram of N10 nozzle after adding ribs

为验证通过增设筋板的方式是否能提高接管局部结构承载性能，通过有限元计算得到了不同筋板厚度下N10接管局部结构的最大等效位移和最大von Mises等效应力，具体如表3所示。

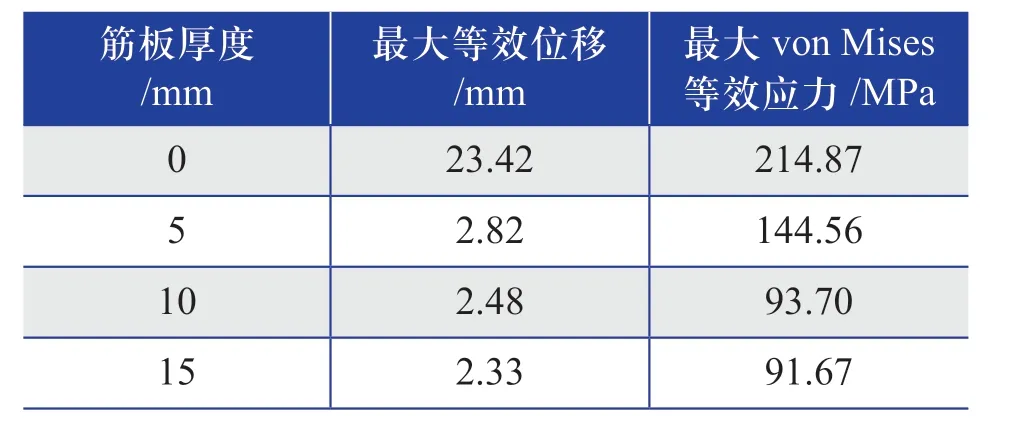
表3 不同筋板厚度下N10接管局部结构的 最大等效位移和最大von Mises等效应力Table 3 Maximum equivalent displacement and maximum von Mises equivalent stress of local structure of N10 nozzle under different stiffener thicknesses

从表3可以看出，增设筋板可以显著降低N10接管局部结构的最大等效位移和最大von Mises等效应力，但随着筋板厚度的增加，其对于降低最大等效位移和最大von Mises等效应力的作用逐渐变得不明显。这表明，从提升结构强度的角度来看，增加筋板能起到提高接管局部结构承载性能的作用，但筋板厚度需控制在一定范围内。

4.2.2 增设补强圈(不设筋板)的影响分析

图9 接管开孔处增设补强圈后N10接管的局部结构 示意图(单位：mm)Fig. 9 Local structure schematic diagram of N10 nozzle after adding a reinforcing ring at opening of nozzle(unit:mm)

不同补强圈厚度下N10接管局部结构的最大等效位移和最大von Mises等效应力如表4所示。

表4 不同补强圈厚度下N10接管局部结构的最大等效位移和最大von Mises等效应力Table 4 Maximum equivalent displacement and maximum von Mises equivalent stress of local structure of N10 nozzle under different thickness of reinforcing ring

从表4可以看出，随着补强圈厚度的增加，N10接管局部结构的最大等效位移和最大von Mises等效应力逐渐降低。这表明，从提升结构强度的角度来看，增加补强圈能有效降低接管局部结构的最大等效位移和最大von Mises等效应力。

5 罐体稳定性及接管荷载对其的影响分析

5.1 罐体的非线性屈曲分析

对于工程中的结构稳定性问题的分析，采用非线性计算更为合理、可靠，因此，本文采用非线性稳定性计算方法计算罐体的临界荷载。计算过程分为2个步骤：1)基于线性屈曲的计算结果，对罐体引入初始缺陷，初始缺陷因子设为0.01。2)在第1)步静力分析的基础上，对罐顶逐渐施加最高可达50 kPa的外压荷载，此步骤采用弧长算法进行非线性迭代计算；当外压荷载施加到9.7 kPa时，非线性计算程序不再收敛，这表明罐体整体结构接近弹塑性失稳的垮塌状态，此时得到罐体的von Mises等效应力和等效位移云图，如图10所示。

图10 施加9.7 kPa外压荷载时罐体的von Mises等效应力和等效位移云图Fig. 10 Cloud diagram of von Mises equivalent stress and equivalent displacement of tank body when 9.7 kPa external pressure load is applied

由图10可知，当外压荷载施加到9.7 kPa时，罐体的最大von Mises等效应力为111.99 MPa，发生在罐壁与罐顶连接处，该值已达到TP347H材料在580 ℃时的屈服应力112 MPa，这表明罐壁与罐顶连接处发生了塑性屈服。最大等效位移发生在罐顶，这是由于罐顶承受过大压缩荷载时发生了一定的弹性变形。根据《ASME boiler & pressure vessel code-section Ⅷ：Rules for construction of pressure vessels，division 2——Alternative rules》中第5.4节的内容，设计系数的取值为2.08，可得到罐体的许用外压力为4.66 kPa；该值大于罐体的设计压力2.0 kPa，因此设计的罐体能满足稳定性的要求。

外压荷载为9.7 kPa时罐壁的von Mises等效应力云图如图11所示。由图可知，罐壁的最大von Mises等效应力达到了112 MPa。

图11 施加9.7 kPa外压荷载时罐壁的von Mises等效应力云图Fig. 11 Cloud diagram of von Mises equivalent stress of tank wall when 9.7 kPa external pressure load is applied

外压荷载为9.7 kPa时，罐顶的von Mises等效应力云图如图12所示。由图可知，罐顶的最大von Mises等效应力为110.15 MPa，该值小于TP347H材料在580 ℃时的屈服应力112 MPa，因此罐顶仍处于弹性范围。

综合图11、图12可知，由于罐壁的最大von Mises等效应力出现在罐顶与罐壁连接处，因此该位置的抗压能力弱于其他部位，这与罐壁上端筒节的壁厚较薄、抗压能力差有关。

图12 施加9.7 kPa外压荷载时罐顶的von Mises 等效应力云图Fig. 12 Cloud diagram of von Mises equivalent stress of tank top when 9.7 kPa external pressure load is applied

5.2 接管荷载对罐体非线性屈曲临界荷载的影响

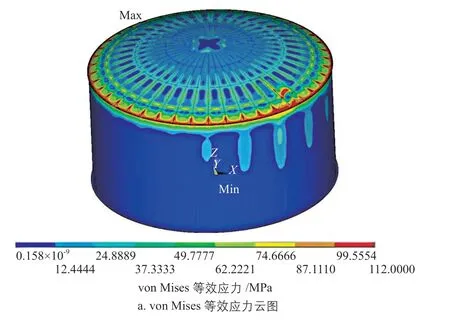
将罐顶3个接管的集中力和扭矩荷载及罐体自重施加到罐体上后，再次进行非线性迭代计算。当外压荷载施加到8.02 kPa时，非线性计算程序不再收敛，这表明罐体整体结构接近弹塑性失稳的垮塌状态，此时得到罐体的von Mises等效应力和等效位移云图如图13所示。由图可知，此时最大von Mises等效应力为112 MPa，发生在罐壁与罐顶连接位置，该值已达到TP347H材料在580 ℃时的屈服应力112 MPa，这表明罐壁与罐顶连接处发生了塑性屈服；最大位移发生在N10接管位置，这是由于该接管受到了较大的外压荷载。根据《ASME boiler & pressure vessel code-section Ⅷ：Rules for construction of pressure vessels，division 2——Alternative rules》中第5.4节的内容，设计系数取2.08，可得到罐体的许用外压力为3.86 kPa；该值大于罐体的设计压力2.0 kPa，因此设计的罐体能满足稳定性的要求。

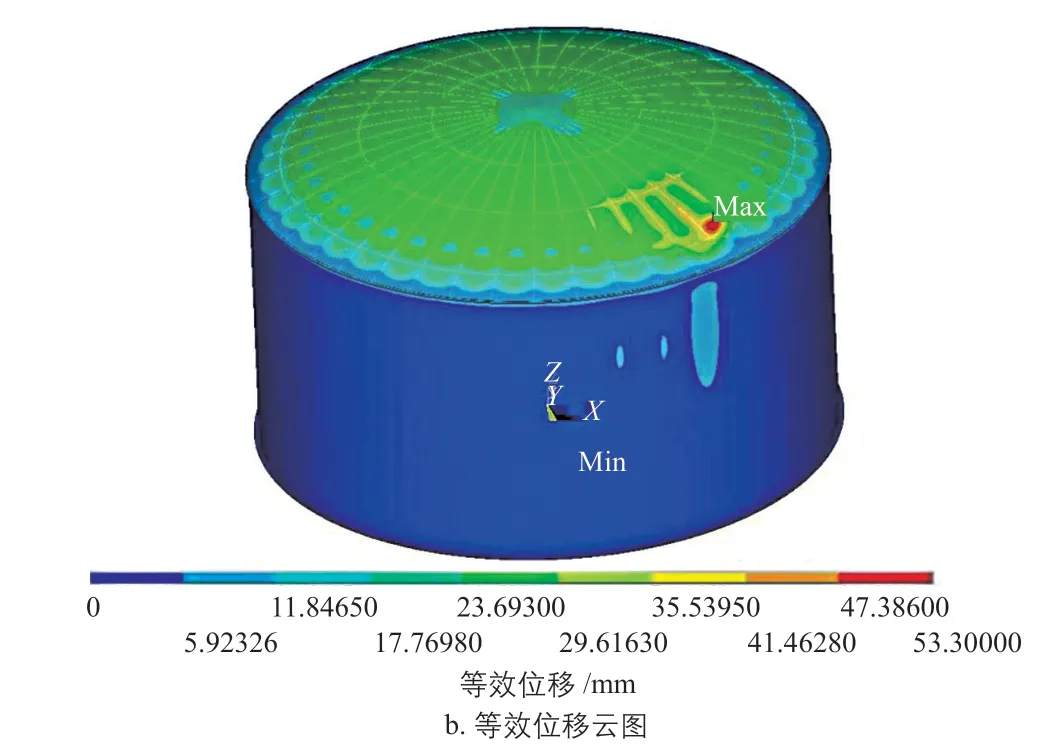
图13 施加8.02 kPa外压荷载时罐体的von Mises等效应力和等效位移云图Fig. 13 Cloud diagram of von Mises equivalent stress and equivalent displacement of tank body when 8.02 kPa external pressure load is applied

施加8.02 kPa外压荷载时罐壁的von Mises等效应力云图如图14所示。由图可知，此时最大von Mises等效应力可达112 MPa。

图14 施加8.02 kPa外压荷载时罐壁的von Mises等效应力云图Fig. 14 Cloud diagram of von Mises equivalent stress of tank wall when 8.02 kPa external pressure load is applied

施加8.02 kPa外压荷载时罐顶的von Mises等效应力云图如图15所示，由图可知，此时最大von Mises等效应力可达112 MPa，发生在罐顶的周边。

通过计算可以发现，施加3个接管荷载及罐体自重后，罐体的许用外压力从4.66 kPa 降至3.86 kPa，但始终大于罐体的设计压力2.0 kPa，因此设计的罐体能满足稳定性的要求。

图15 施加8.02 kPa外压荷载时罐顶的von Mises等效应力云图Fig. 15 Cloud diagram of von Mises equivalent stress of tank top when 8.02 kPa external pressure load is applied

6 结论

本文以青海省某塔式太阳能热发电站中直径为25 m的高温熔盐储罐(储热罐)为例，对储罐罐顶接管的强度及其对罐体稳定性的影响进行了分析，结果表明：

1)对罐体施加熔盐静压、罐体和保温层自重，以及罐顶接管的集中力和扭矩荷载后，最大等效位移为11.14 mm，最大von Mises等效应力为93.54 MPa，均位于N10接管的位置；此时罐体处于弹性范围内，罐体整体结构较为安全。

2)接管现有的加筋结构造成接管与罐顶连接处存在过大的集中应力和局部应力，易引起接管局部结构的热疲劳失效。

3)从提升接管结构强度的角度来看，采用增加接管周边筋板和增设补强圈的方式，可降低局部应力。

4)通过非线性屈曲分析发现，对罐体施加3个接管荷载及罐体自重后，罐体稳定性垮塌荷载为8.02 kPa；设计系数的取值为2.08，得到罐体的许用外压力为3.86 kPa。

5)对罐体进行非线性屈曲分析时发现，最大von Mises等效应力出现在罐顶和罐体连接处，这表明罐顶与罐壁连接处的抗压能力弱于罐体其他部位。

针对本文的分析结果，建议在后续设计熔盐储罐时采取以下措施：1)接管周边增设筋板和补强圈。2)根据上述改进后的接管结构，重新进行有限元计算，对接管周边的最大von Mises等效应力进行合理控制，以确保罐顶上的接管周边不发生热疲劳失效。3)虽然现有的罐体结构可满足稳定性要求，但若要进一步提升罐体的稳定性性能，建议增加罐壁上端的厚度，或在罐壁上端一定范围内增加抗风圈。