风电场测风数据插补方法研究及插补结果偏差分析

2021-03-04于佳鹤王风涛

太阳能 2021年2期

于佳鹤，崔杰，王风涛

(北京金风科创风电设备有限公司，北京 100176)

0 引言

风电场测风数据是影响风电场产能评估的最直接因素[1]。依据GB/T 18710-2002《风电场风能资源评估方法》[2]，测风塔数据需要有1个完整年的测量时间。但实际情况中，由于测风塔仪器损坏、数据传输故障、结冰、倒塔等原因，会造成测风塔数据中存在大量的问题数据[3]。因此，为客观反映风电场的风资源情况，需对测风塔数据进行清洗然后补全，将测风塔数据补全至1个完整年。另外，由于测风工作占据了风电项目前期阶段的大量时间，若能在实测数据测量时间较短的情况下提供合理且快速的将数据补全的方法，有助于较快得到完整年的数据，从而进行风电项目资源的初步评估，这将有利于提升风电项目的开发效率[4]。这种将数据补全的方法即为插补方法[5-6]，可根据参考数据利用插补方法将目标数据补全。

本文对数据插补的相关应用进行了探究，从相关系数、测风时间、插补算法3个方面进行了分析，目的是探究适合做插补的相关系数水平；研究了不同测风时长及不同测风月份时的偏差水平及偏差关系，在测风时长一定的前提下，推荐了最优的测风月份，并针对不同测风数据的均方误差(mean-square error，MSE)值推荐了最优插补算法。

1 数据收集及插补方法

1.1 数据收集

为了评价插补方法的优劣，在全国范围内收集满足有效率要求的450对测风塔的样本数据互相作为目标塔和参照塔。样本数据需要满足以下要求：1)每座测风塔的样本数据满足1个完整年，且数据有效率满足GB/T 18710-2002《风电场风能资源评估方法》的要求；2)每对测风塔样本数据同期测量时间满足1个完整年。

按照既定目标对目标塔的数据进行剔除，从而模拟真实数据缺失的案例；使用参照塔数据，采用不同的测量-关联-预测(Measure-Correlate-Predict，MCP)[7]方法对目标塔数据进行插补；然后将插补结果与真实数据进行对比。

1.2 MCP插补方法介绍

本文进行对比分析的MCP插补方法有8种算法，包括线性最小二乘(linear least squares，LLS)法、正交最小二乘(total least squares，TLS)法、方差比(variance ratio，VR)法[8]、速度比(bulk speed ratio，BSR)法、威布尔分布拟合(Weibull fit，WBL)法[9]、风速排序(speed sort，SS)法[10]、垂直切片(vertical slice，VS)法[11]，以及矩阵时间序列(matrix time series，MTS)法[12]。

1.2.1 线性最小二乘(LLS)法

此算法的原理是在目标风速与参考风速散点基础上得到线性直线的斜率和截距，LLS法最小化的是数据点到最佳拟合线的垂直距离的误差平方和。

采用LLS法可选的参数有“扇区数量”和“截取风速”。如果扇区数量大于1，即为分扇区插补，此时在根据参考数据划分的扇区内利用LLS法分别对参考风速进行拟合；如果设置了截取风速，则在直线拟合过程中忽略目标风速和参考风速小于截取风速的散点。

1.2.2 正交最小二乘(TLS)法

TLS法是在LLS法的基础上对偏差的计算方法进行了改进，使数据点到最佳拟合直线的正交距离最小，以此来拟合斜率和截距，从而得到直线方程。

采用TLS法有2个可选的参数，即“扇区数量”和“截取风速”。

1.2.3 方差比(VR)法[8]

VR法是一种利用同期数据平均值和方差比来表示线性模型的斜率和截距的线性方程。简单的线性回归模型预测的平均风速值与实测的平均风速值十分接近，但其预测的风速序列的方差却小于实测的风速序列的方差，如此可能导致风频分布预测出现偏差。VR法预测的风速序列与实测的风速序列具有相同的平均值和方差，可以很好地解决上述问题。

采用VR法有2个可选的参数，即“扇区数量”和“截取风速”。

1.2.4 速度比(BSR)法

BSR法是一种非常简单的将目标风速序列与参考风速序列关联起来的算法，这种算法是假设目标风速与参考风速之间的关系为y=bx，其中，斜率项b等于目标风速序列和参考风速序列的比值。

采用BSR法有2个可选的参数，即“扇区数量”和“截取风速”。

1.2.5 威布尔分布拟合(WBL)法[9]

WBL法致力于建立目标风速序列的分布参数与参考风速序列的分布参数之间的线性关系。该算法适用于目标风速序列与参考风速序列均较好的满足威布尔分布的情况，但是明显是非威布尔分布时误差较大。

采用WBL法只有1个可选的参数，即“扇区数量”。

1.2.6 风速排序(SS)法[10]

SS法是在LLS法的基础上引入了排序的思想，与传统的线性回归法不同，SS法将各扇区中参考风速序列与目标风速序列进行独立排序，得到排序后的新数据序列中目标风速关于参考风速的分布散点，针对分布散点拟合线性回归方程。

采用SS法仅有1个可选的参数，为“扇区数量”。

1.2.7 垂直切片(VS)法[11]

VS法是在传统的线性模型中引入分段的思想，将扇区中参考风速与目标风速的同期数据按照数据大小进行分组，建立分段线性模型，然后通过细化数据段，提高模型的拟合优度。

采用VS法只有1个可选的参数，为“扇区数量”。

1.2.8 矩阵时间序列(MTS)法[12]

MTS法是基于经典矩阵法的改造，该算法的目标是生成目标数据的真实分布，由于无需考虑目标风速与参考风速的相对分布，因此其能得到较好的目标风速的分布情况，且可以在目标风速序列与参考风速序列相关性较差的情况下预测目标风速序列。相较于大多数线性MCP方法，这种对目标风速分布的关注是MTS法的主要优势，但由于测风记录是以散点的形式保存的，因此该算法在得到连续型联合概率密度分布函数时会引入拟合的不确定性。

2 评价指标与均值检验

为综合评价不同插补算法得到的插补结果的优劣，本文采用MSE值、威布尔分布k值[13]、平均风速、风功率密度[14]、风电机组发电量这5种不同类型的指标作为评价指标，并利用评价指标构建相对偏差及绝对偏差指标体系用于结果分析；最后为验证偏差结果之间是否存在显著性差异，对偏差结果进行均值检验。

2.1 分析评价指标

1)MSE值。MSE是预测数据点和真实数据点误差的平方和的均值，用来检测模型的预测值和真实值之间的偏差；MSE值越大，表明预测效果越差。MSE的公式为：

式中，m为数据量；i为第i个数据点；yi为真实数据点；y^i)为预测数据点。

2)威布尔分布k值(下文简称“k值”)[13]。k为威布尔分布的形状参数，是度量风频分布的指标。威布尔分布模型可以很好地模拟风速的分布情况，风速分布的概率密度函数f(v)为：

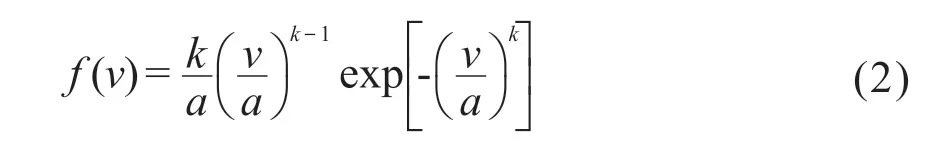
式中，a为尺度参数；v为风速。

3)平均风速。平均风速是指风速序列的平均值，其计算公式为：

式中，μ为平均风速；n为样本量。

4)风功率密度[14]。风功率密度是用来评价风做功能力的指标，指单位时间内通过单位叶轮面积的空气动能。风功率密度Pv的公式为：

式中，ρ为空气密度。

5)风电机组发电量(标准发电小时数)。利用北京金风科创风电设备有限公司生产的GW140/2500风电机组的功率曲线进行产能计算，从而可以直观地反映出插补偏差带来的发电量影响。

2.2 均值检验[15-16]

均值检验的目的是检验2个或2个以上总体分布的均值是否存在显著性差异，以“2个或2个以上独立样本来自的2个或2个以上总体分布的均值无显著性差异”作为原假设。当样本组为2组时，采用Welch均值检验方法；当样本组的组数超过2组达到3组及3组以上时，则为多样本检验，此时采用Kruskal-Wallis均值检验方法。

采用Welch均值检验方法时应用的检验统计量为t统计量，即：

其中，

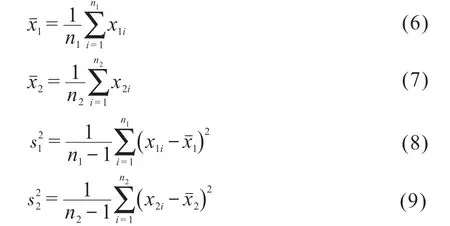
采用Kruskal-Wallis均值检验方法时应用的统计量为K-W统计量，即：

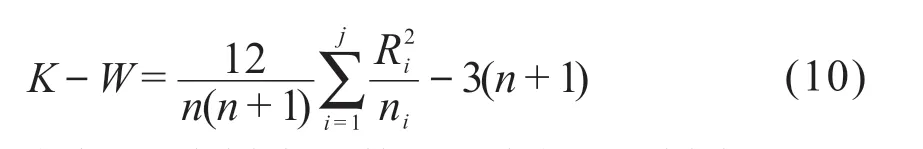
式中，j为样本组数；ni为第i组样本量；Ri为第i组样本中的秩总和。

定义均值检验的显著水平α=0.05，均值检验的显著水平结果为p。当p≤α时，拒绝原假设，认为样本数据组来自不同的分布，即分布的均值存在显著性差异。

3 结果分析

本文就相关系数、测风时间及插补算法3个部分对测风数据插补结果的偏差进行分析。

3.1 相关系数

相关系数分析采用指标MSE作为评价标准，MSE是度量整个序列插补效果优劣的评价指标。通过对测试结果进行分析发现，样本数据之间相关系数的平方R2与MSE之间的线性相关系数为-0.55，属于中度线性相关；这意味着若样本数据之间的R2越大，则MSE的值就越小，即说明插补的结果越优。

利用R2与MSE的数据建立线性模型，即：

所有插补结果的MSE平均水平约为3.5，与之对应的R2约为0.65。因此就MSE而言，如果插补的结果要达到平均水平，R2至少应在0.65以上。

根据相关系数分析结果来选择用于测风时间和插补算法分析的测试数据。

3.2 测风时间

通过对测风时长的主要评价指标进行相对偏差分析，并对主要评价指标的相对偏差值进行均值检验，可得出不同测风时长时各主要评价指标的相对偏差值之间的关系；其次是对测风时长的MSE及主要评价指标进行绝对偏差分析，并且对MSE及主要评价指标的绝对偏差值进行均值检验，可得出不同测风时长的MSE及主要评价指标的绝对偏差均值的具体数值；最后对相同测风时长的不同测风月份的相对偏差、MSE和绝对偏差进行分析并进行均值检验，得出在测风时长一定的情况下的最优测风月份。

3.2.1 相对偏差分析

不同测风时长时各主要评价指标的相对偏差分析结果如表1及图1所示。表中数据均为对应测风时长下各主要评价指标的相对偏差测试结果的均值。

对表1中各主要评价指标的相对偏差值进行均值检验。检验结果表明，全年的主要评价指标相对偏差值的均值检验结果p均为零，意味着测风时长不同会导致全年的主要评价指标相对偏差值的均值结果不同；插补部分的主要评价指标相对偏差值的均值检验结果p均为1，意味着测风时长不同不会导致插补部分的主要评价指标相对偏差值均值结果的不同。

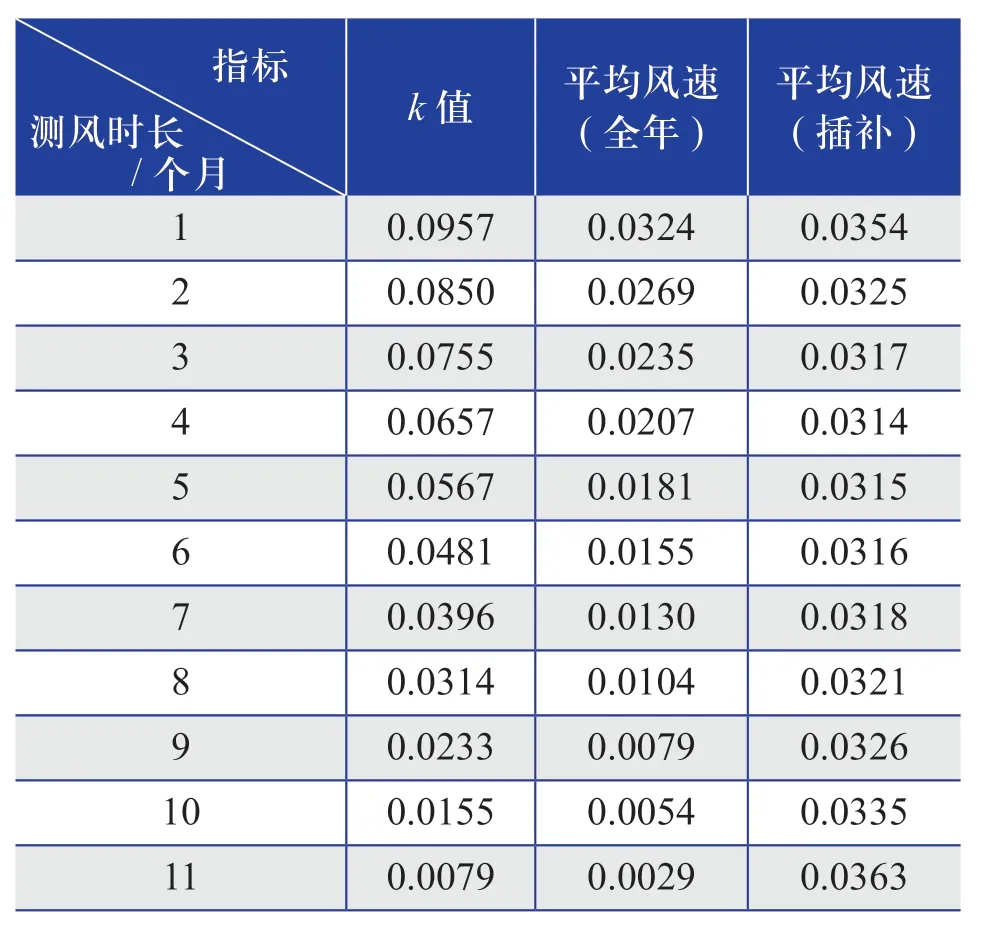
表1 不同测风时长时主要评价指标的相对偏差值Table 1 Relative deviation value of main evaluation indexes with different wind measurement duration

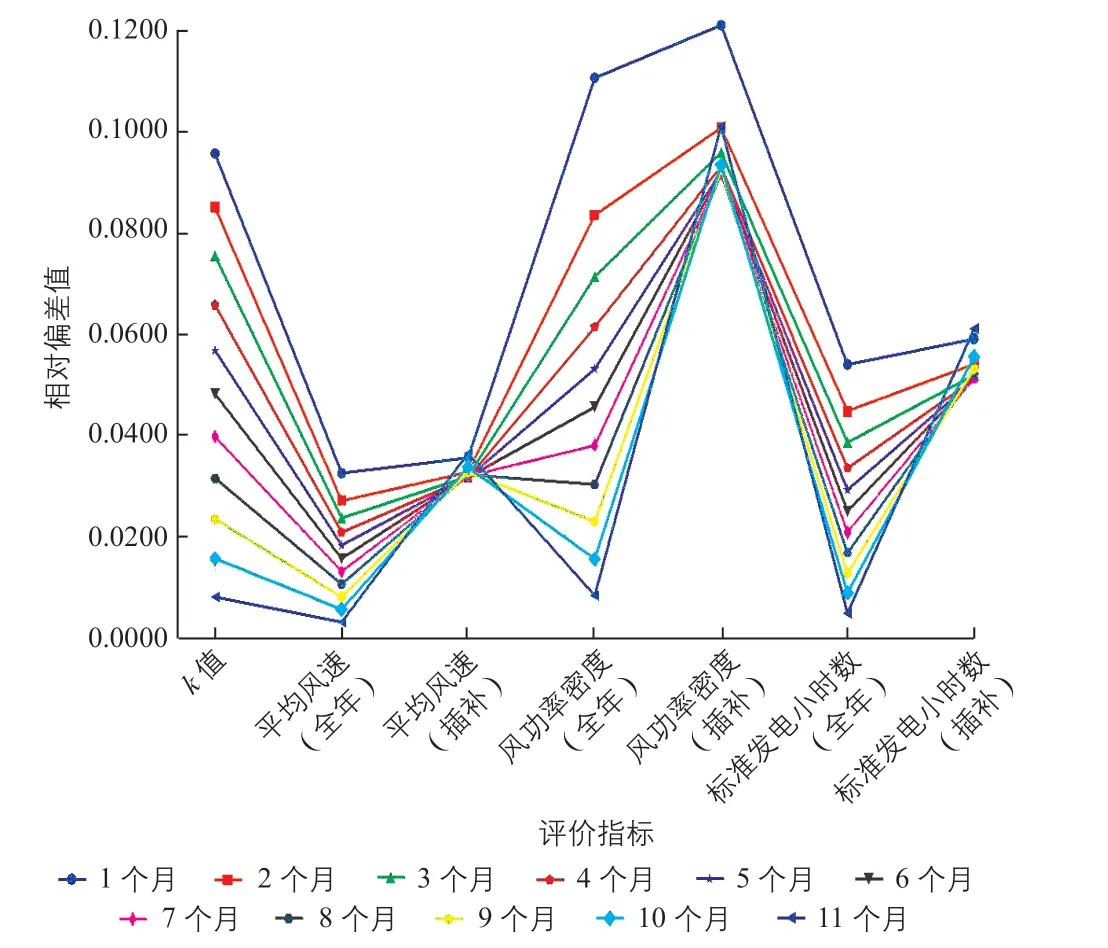
图1 不同测风时长时主要评价指标的相对偏差值对比Fig. 1 Comparation of relative deviation of main evaluation indexes with different wind measurement duration

从图1及表1的数据结果来看，对于全年的主要评价指标相对偏差值来说，测风时长越长，全年的主要评价指标相对偏差值越小；但就插补部分的主要评价指标相对偏差值而言，并不是测风时长越长，其主要评价指标相对偏差值就越小，而是在测风时长为4个月左右时，插补部分的主要评价指标相对偏差值较小。

3.2.2MSE及绝对偏差分析

为进行各测风时长之间各主要评价指标绝对偏差的对比，绝对偏差仅计算全年的绝对偏差，因此以下分析所采用的绝对偏差全部为全年的绝对偏差。不同测风时长时MSE及主要评价指标的绝对偏差分析结果如表2所示。表中除MSE所对应的数据之外，其他数据均为对应测风时长下主要评价指标绝对偏差测试结果的均值。

对表2中MSE及主要评价指标的绝对偏差值进行均值检验。检验结果表明，MSE及主要评价指标绝对偏差值的均值检验结果p均为零，意味着不同测风时长的MSE及主要评价指标绝对偏差值序列之间有显著性差异，测风时长不同会导致MSE及主要评价指标绝对偏差值均值的结果不同。

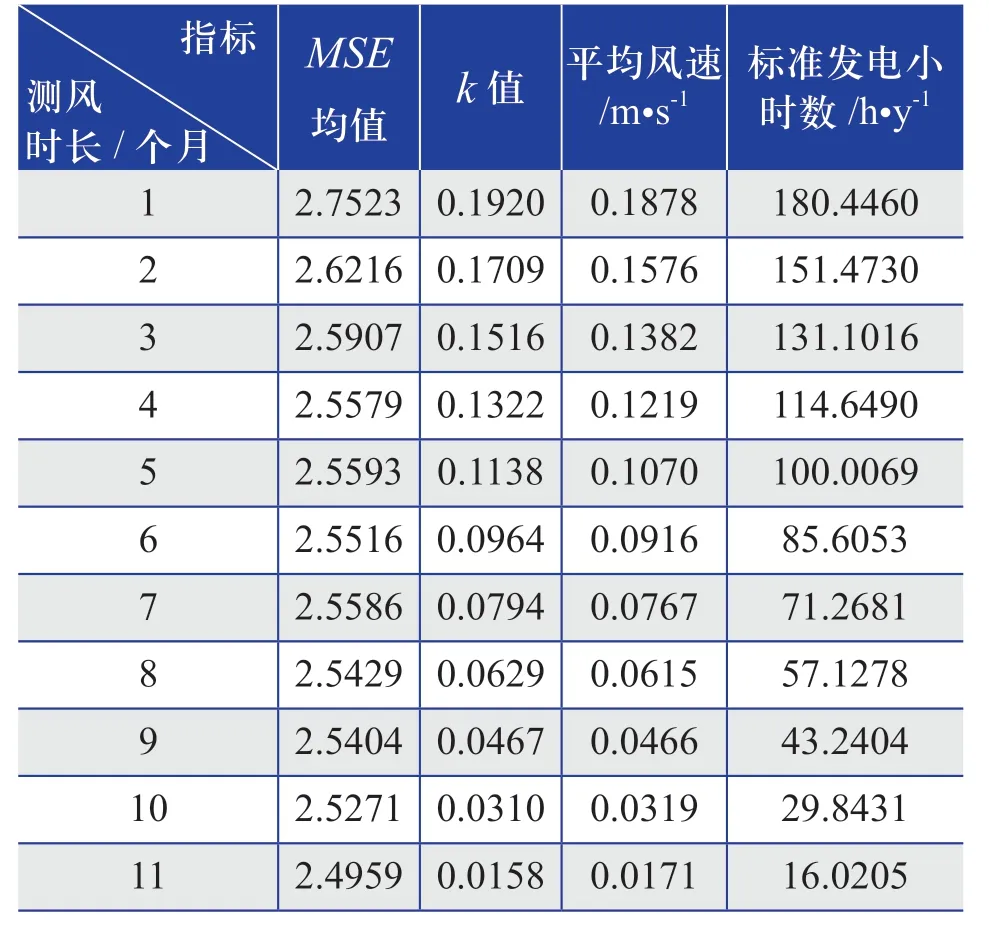
表2 不同测风时长时MSE及主要评价指标的绝对偏差值Table 2 Absolute deviation of MSE and evaluation main indexes with different wind measurement duration

从表2中的结果可以看出，测风时长越长，各主要评价指标绝对偏差值越小，但MSE均值略有不同。图2为MSE值的分布及其均值曲线的组合图形。

图2中的小提琴图反映了MSE值的分布情况，其值参考左纵轴。从图中可以看出，MSE值大多集中在数值较小的区域，只有个别数值较大。查看个别MSE数值较大时的情况是：测风时间较短，设置的扇区多数是12或16个扇区，插补多应用的是MTS法，这样会导致模型训练时的训练数据较少，得到的模型不具有代表性，因此插补序列值与真实值偏差较大。

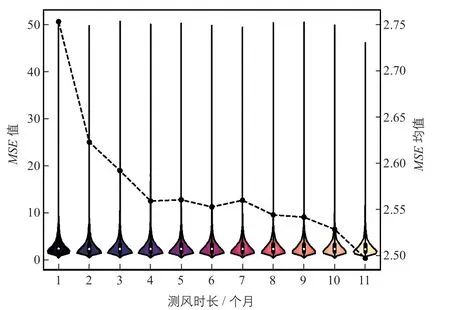
图2 MSE值的分布及其均值曲线Fig. 2 Distribution of MSE value and its mean value curve

图2中的折线图反映了MSE均值的情况，其值参考右纵轴，折线图中每个点对应的是表2中的MSE均值。从图中可以看出，在测风时长小于4个月时，测风时长越长，MSE均值越小；而测风时长在4～7个月之间时，MSE均值稳定在一定水平；测风时长在7～11个月之间时，随着测风时长的增加，MSE均值逐渐减小。另外，测风时长从1个月延长至2个月时，MSE均值下降的幅度很大；直到测风时长为4个月时，MSE均值一直在下降，但下降的幅度较小；测风时长为4个月之后，MSE均值总体下降的程度很小。因此，根据对MSE的分析结果，测风时长至少为2个月，若有条件最好为4个月。

3.2.3 偏差分析及最优测风月份推荐

对相同测风时长的不同测风月份的相对偏差、MSE及绝对偏差进行均值检验，判断相同测风时长的不同测风月份的偏差结果之间是否存在显著性差异。检验结果表明，当测风时长为1、7、8、9、10、11个月时，不同测风月份的偏差结果之间无显著性差异，说明这几个测风时长下测风月份对偏差结果无影响；当测风时长为2、3、4、5、6个月时，不同测风月份的偏差结果之间存在显著性差异，说明这几个测风时长下测风月份不同会导致偏差结果的不同。

虽然相同测风时长的不同测风月份的偏差结果之间有的存在显著性差异，有的不存在显著性差异，但根据最终的全部偏差结果可以进行相同测风时长条件下最优测风月份的推荐。

最优测风月份推荐采用全部偏差的结果，包括相对偏差、MSE及绝对偏差的结果。对各种偏差进行标准化处理，然后对相同测风月份的偏差求和，取标准化后各偏差之和最小的测风月份为此测风时长下的最优测风月份。对每个测风时长的偏差数据进行上述处理，可以得出不同测风时长下的最优测风月份，具体如表3所示。

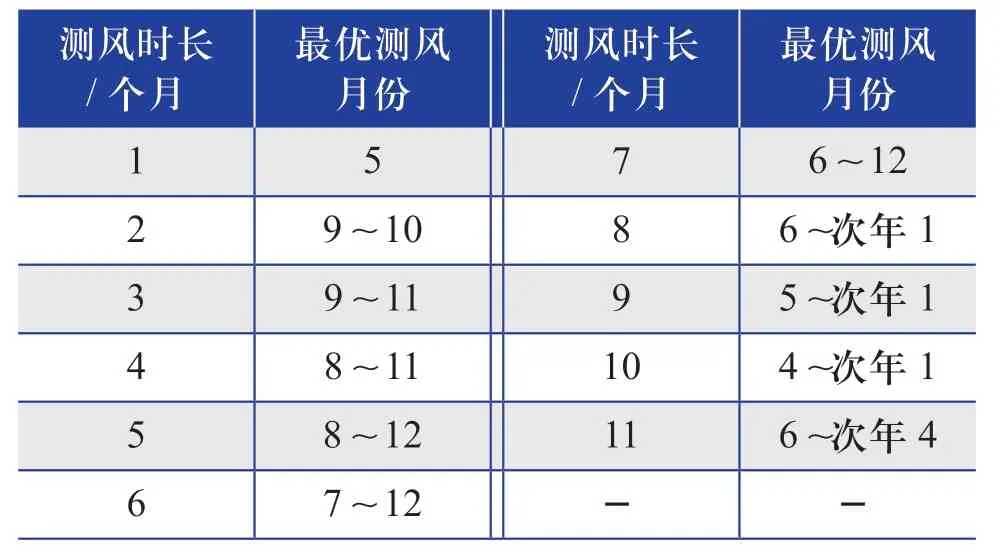
表3 不同测风时长对应的最优测风月份Table 3 Optimal wind measurement month corresponding to different wind measurement duration

3.3 插补算法

插补算法分析的目的是根据数据的测风时长推荐最优算法，以及根据数据的最优测风月份推荐最优算法。MSE是度量整个序列插补结果优劣的标准，因此在进行算法推荐时，仅采用MSE的结果进行插补算法推荐。

3.3.1 测风时长相同

对相同测风时长下采用不同算法的MSE结果进行均值检验。检验结果表明，当测风时长为1、7、8、9、10、11个月时，不同算法的MSE值之间无显著性差异，这说明采用不同算法对MSE值无影响；当测风时长为2、3、4、5、6个月时，不同算法的MSE值之间存在显著性差异，即相同测风时长下采用不同插补算法得到的插补结果的MSE值不同。

即便相同测风时长下采用不同算法的MSE值的均值检验结果之间有的存在显著性差异，有的不存在显著性差异，但根据最终的全部MSE值可以进行最优插补算法的推荐。

对相同测风时长下采用不同算法的MSE值进行分析，针对每个测风时长的最优插补算法进行推荐，推荐算法的结果如表4所示。

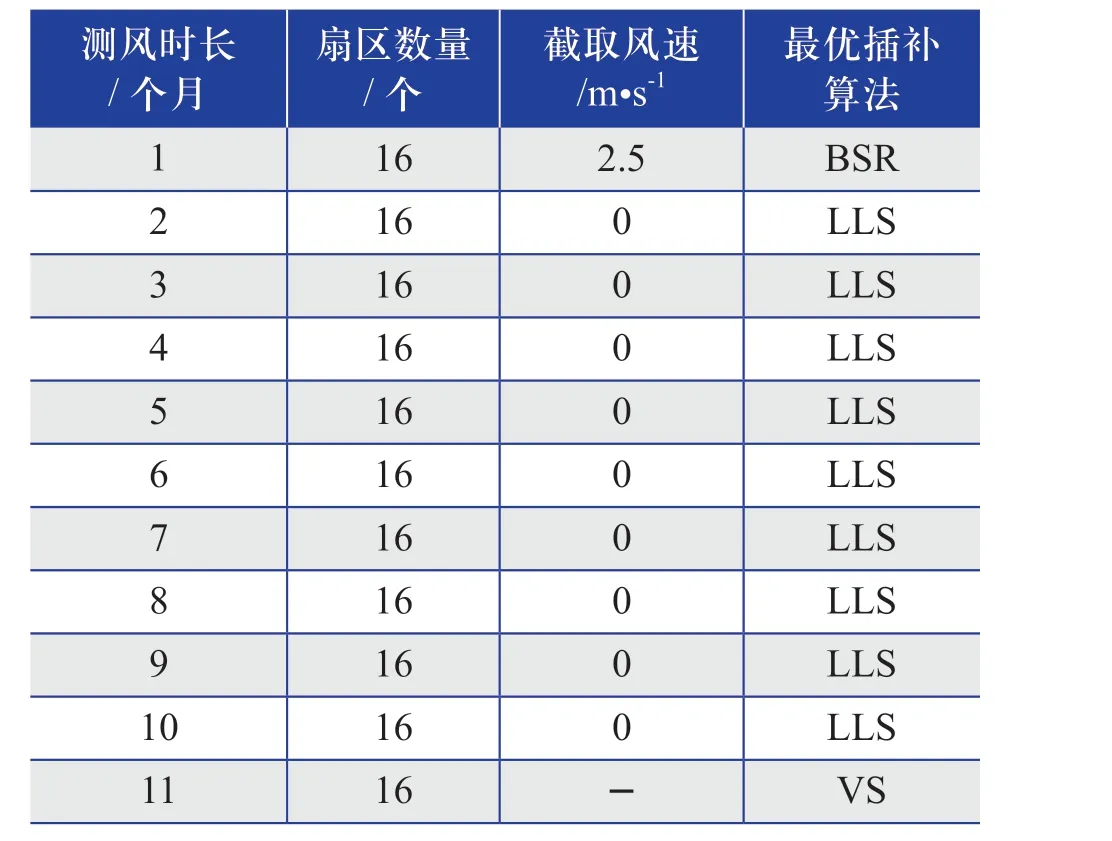
表4 每个测风时长下的最优插补算法结果Table 4 Results of optimal interpolation algorithm for each wind measurement duration

3.3.2 测风月份相同

对相同测风月份下采用不同算法的MSE值进行均值检验。检验结果表明，相同测风月份下采用不同算法的MSE值之间存在显著性差异，意味着就MSE指标而言，测风月份相同时，不同插补算法得到的插补结果的MSE值不同。

对不同测风时长下，相同测风月份采用不同算法的MSE值进行分析，并针对不同测风时长时每个测风月份进行最优插补算法推荐，推荐结果如表5～表15所示。

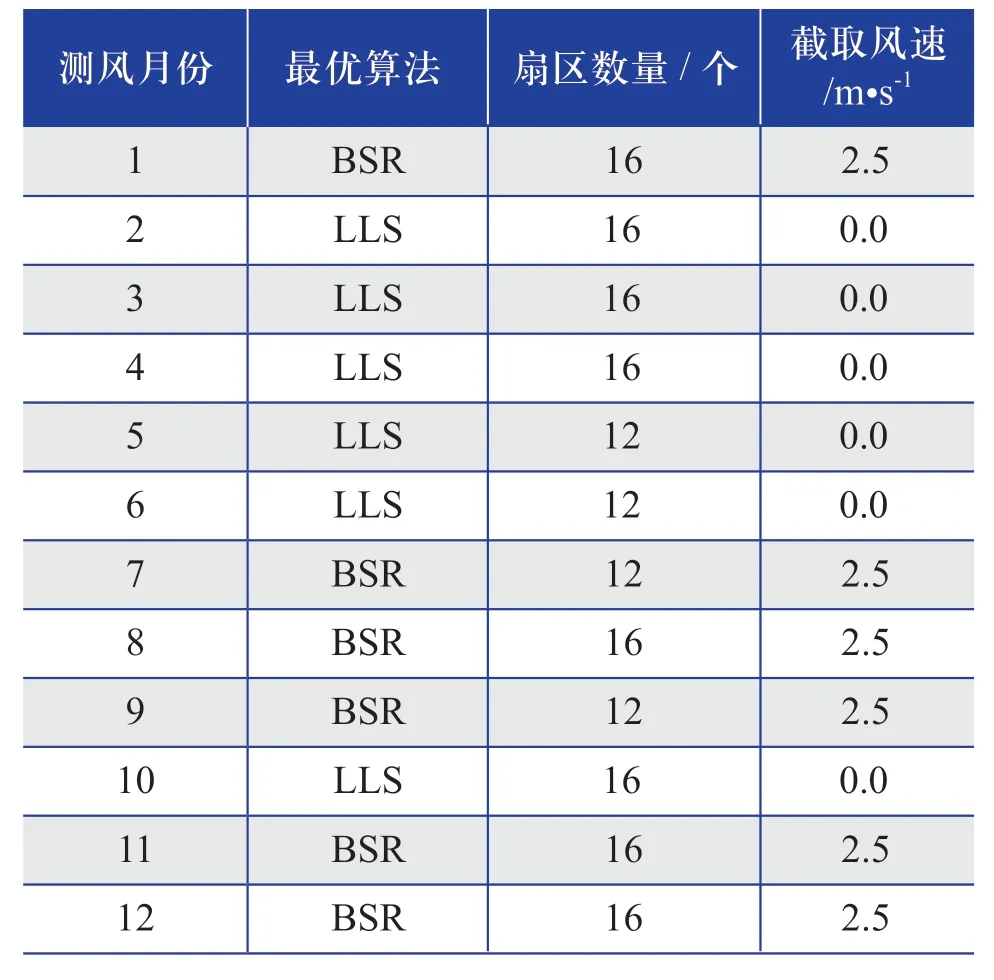
表5 相同测风月份(测风时长为1个月) 最优插补算法的结果Table 5 Results of optimal interpolation algorithm of the same wind measurement month (wind measurement duration is 1 month)

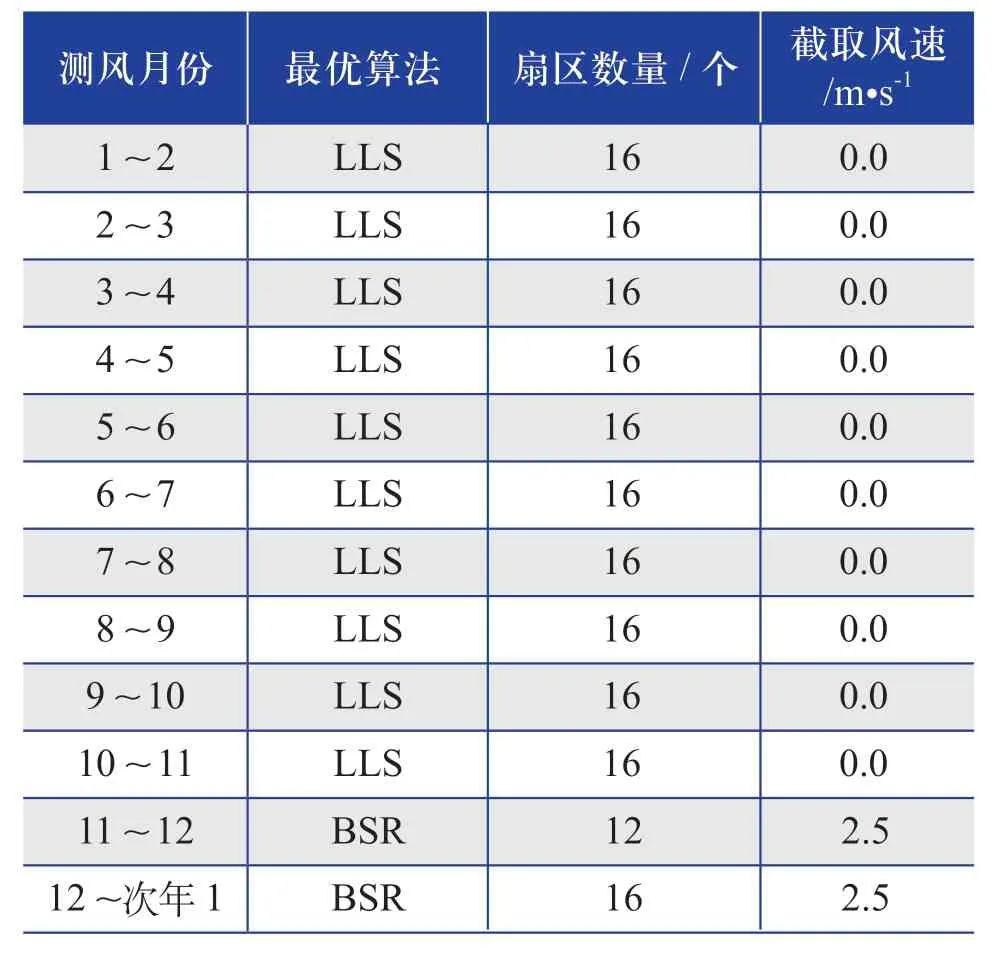
表6 相同测风月份(测风时长为2个月) 最优插补算法的结果Table 6 Results of optimal interpolation algorithm of the same wind measurement month (wind measurement duration is 2 months)

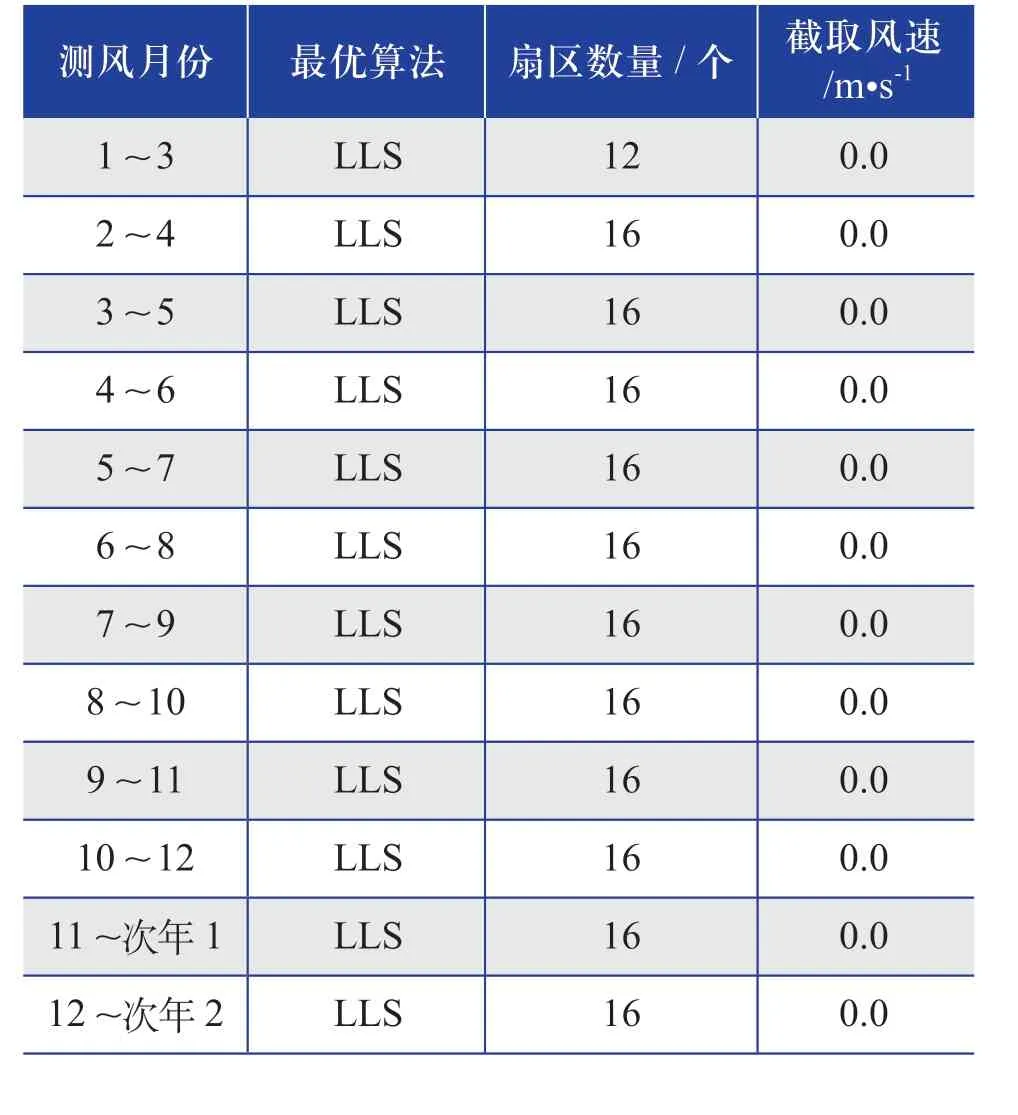
表7 相同测风月份(测风时长为3个月) 最优插补算法的结果Table 7 Results of optimal interpolation algorithm of the same wind measurement month (wind measurement duration is 3 months)

表8 相同测风月份(测风时长为4个月) 最优插补算法的结果Table 8 Results of optimal interpolation algorithm of the same wind measurement month (wind measurement duration is 4 months)

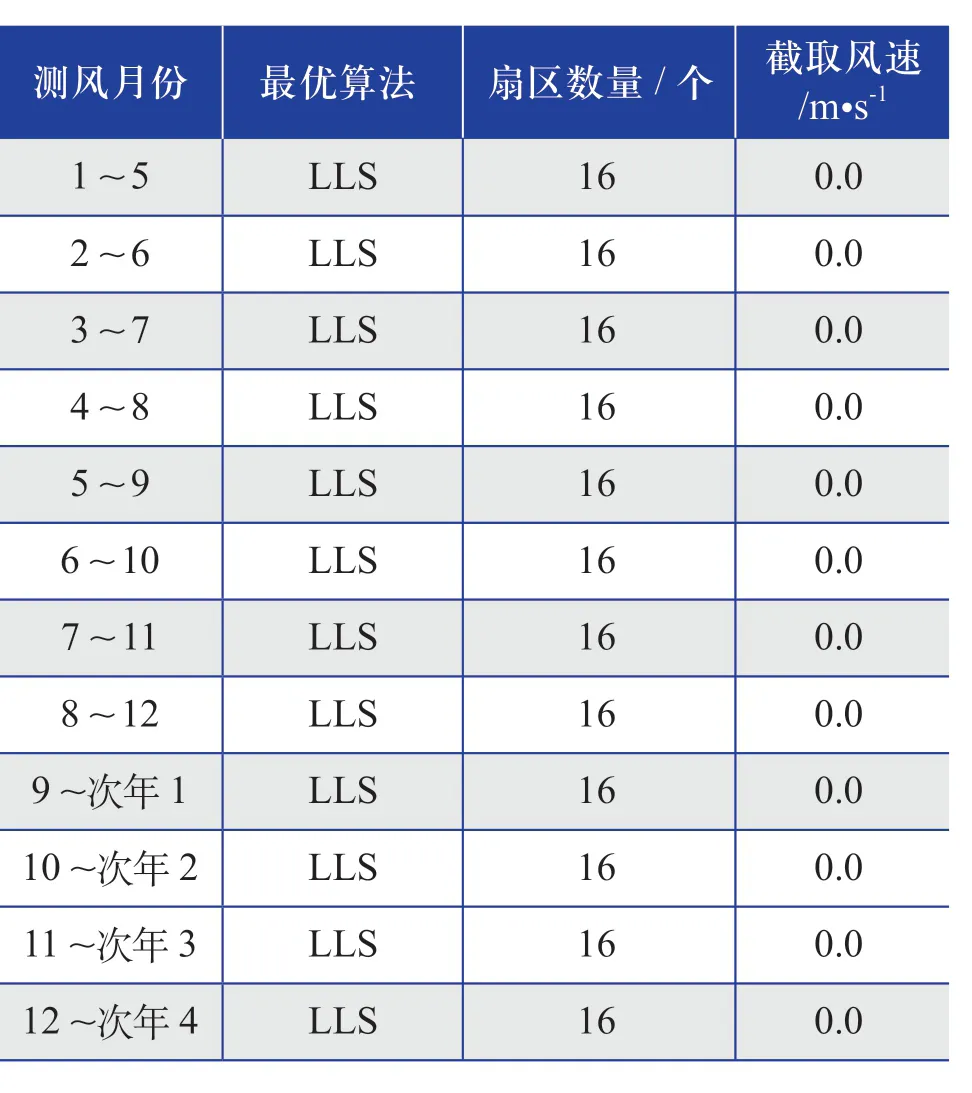
表9 相同测风月份(测风时长为5个月) 最优插补算法的结果Table 9 Results of optimal interpolation algorithm of the same wind measurement month (wind measurement duration is 5 months)

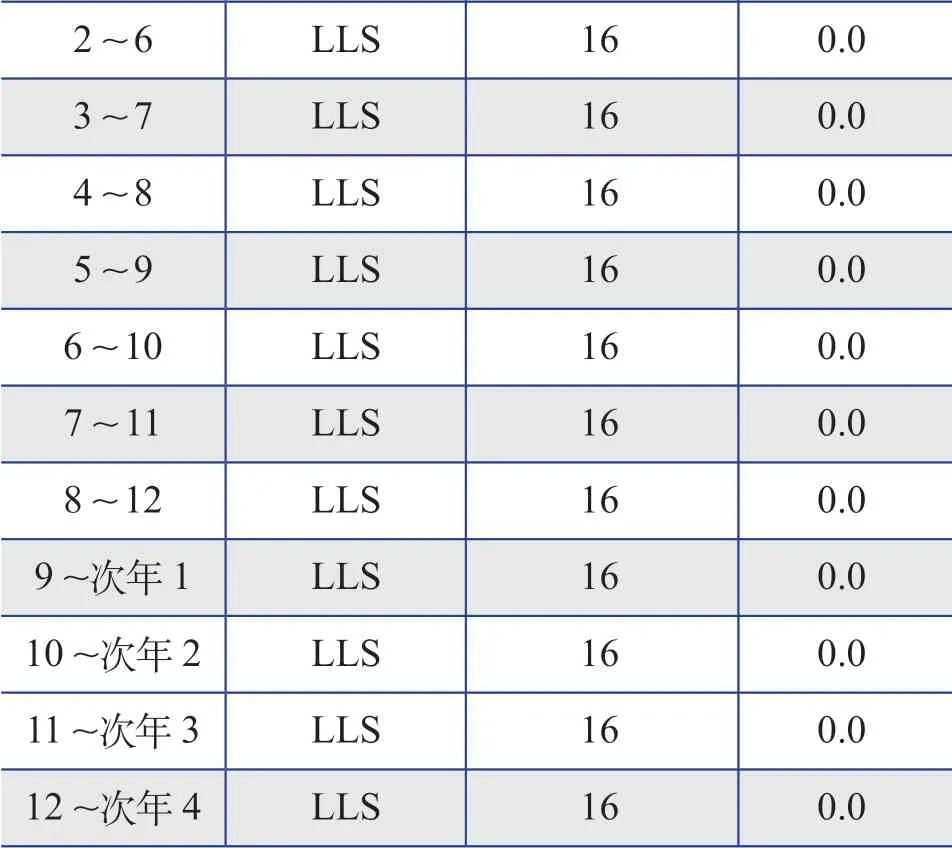
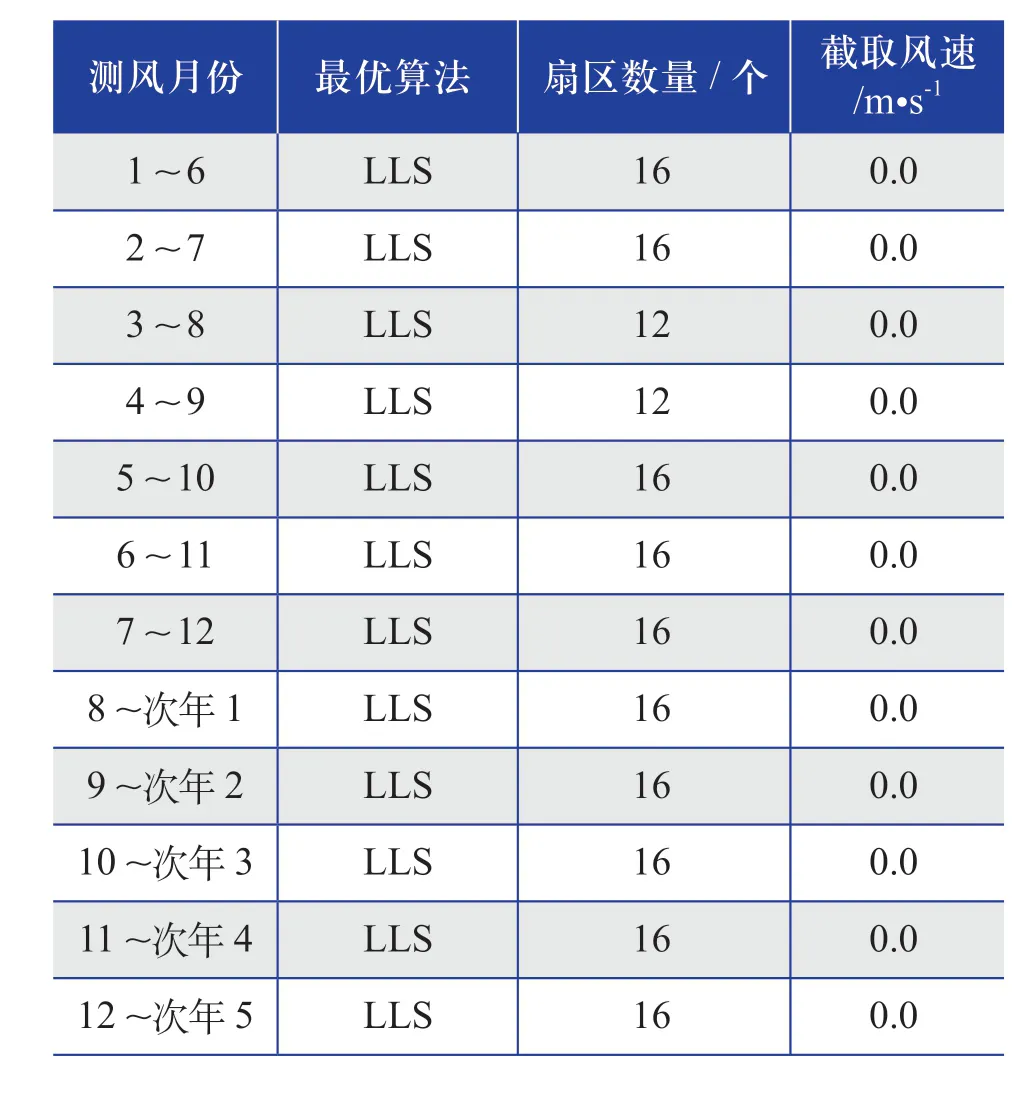
表10 相同测风月份(测风时长为6个月) 最优插补算法的结果Table 10 Results of optimal interpolation algorithm of the same wind measurement month (wind measurement duration is 6 months)

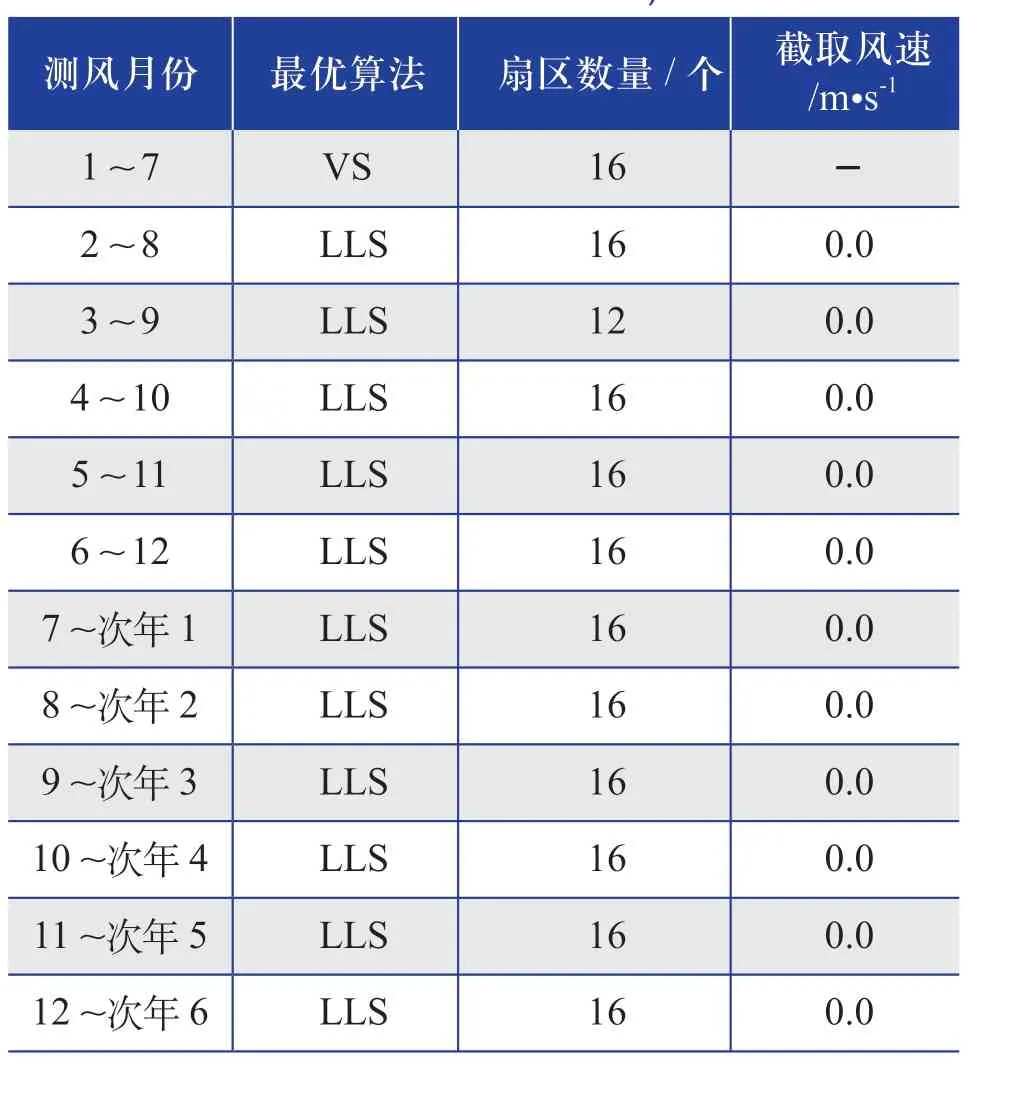
表11 相同测风月份(测风时长为7个月) 最优插补算法的结果Table 11 Results of optimal interpolation algorithm of the same wind measurement month (wind measurement duration is 7 months)

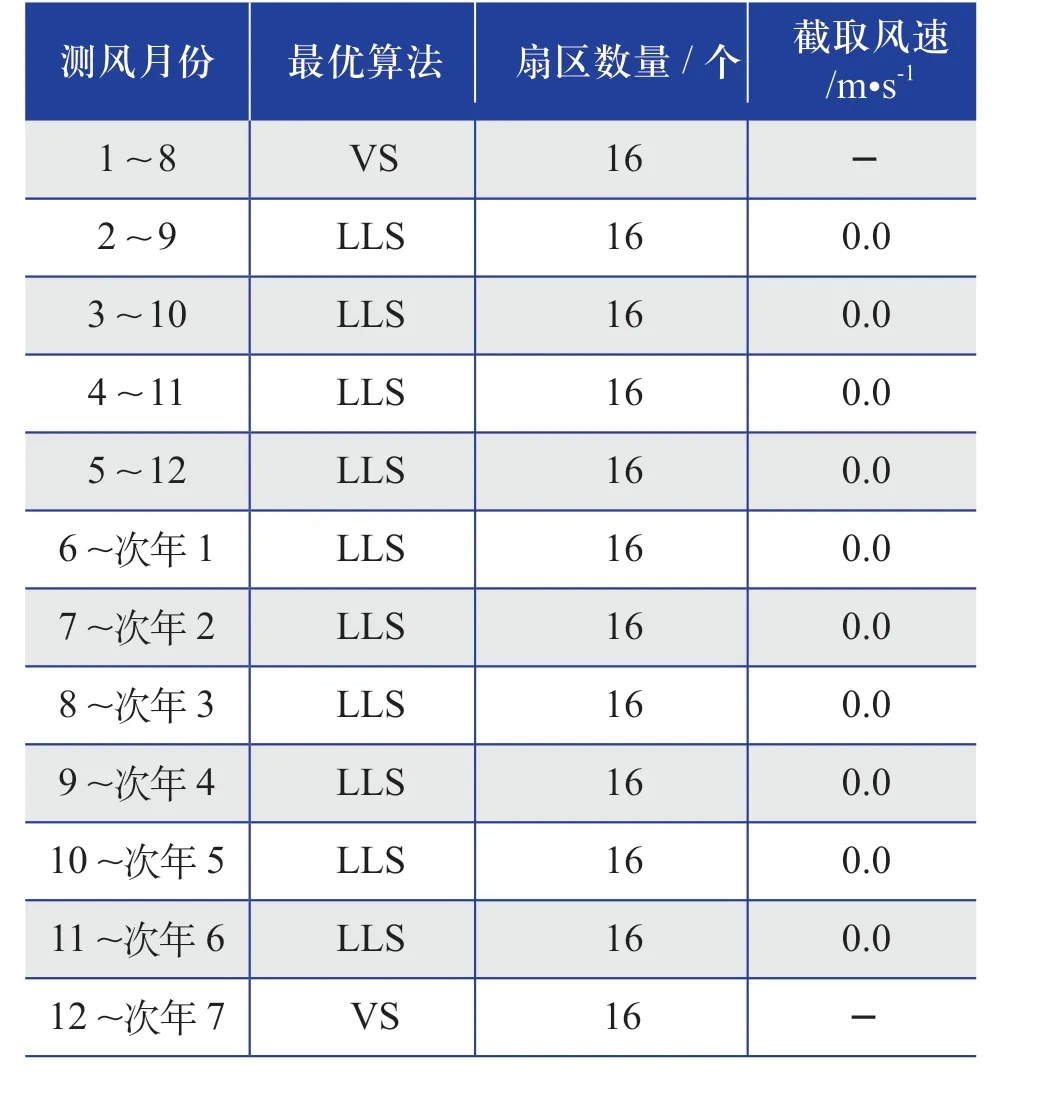
表12 相同测风月份(测风时长为8个月) 最优插补算法的结果Table 12 Results of optimal interpolation algorithm of the same wind measurement month (wind measurement duration is 8 months)

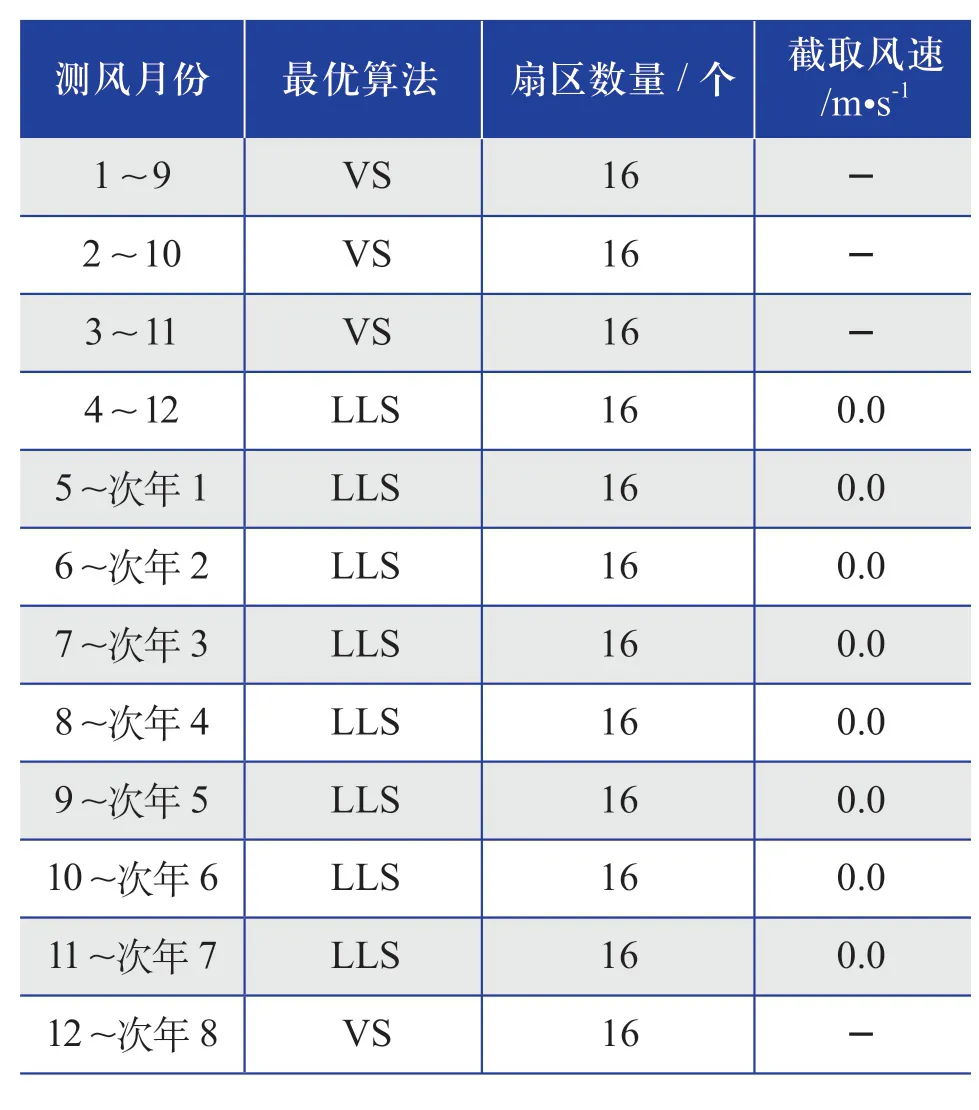
表13 相同测风月份(测风时长为9个月) 最优插补算法的结果Table 13 Results of optimal interpolation algorithm of the same wind measurement month (wind measurement duration is 9 months)

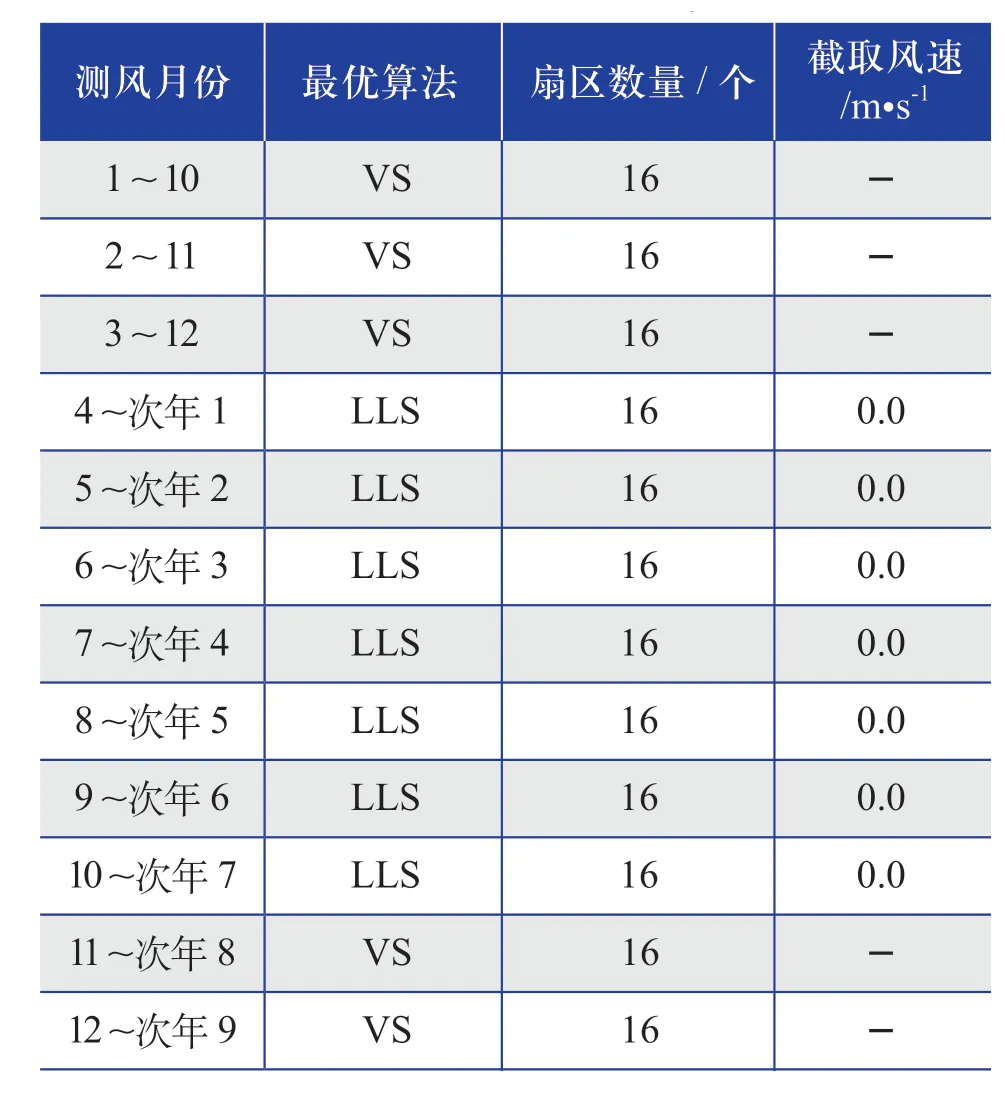
表14 相同测风月份(测风时长为10个月) 最优插补算法的结果Table 14 Results of optimal interpolation algorithm of the same wind measurement month (wind measurement duration is 10 months)

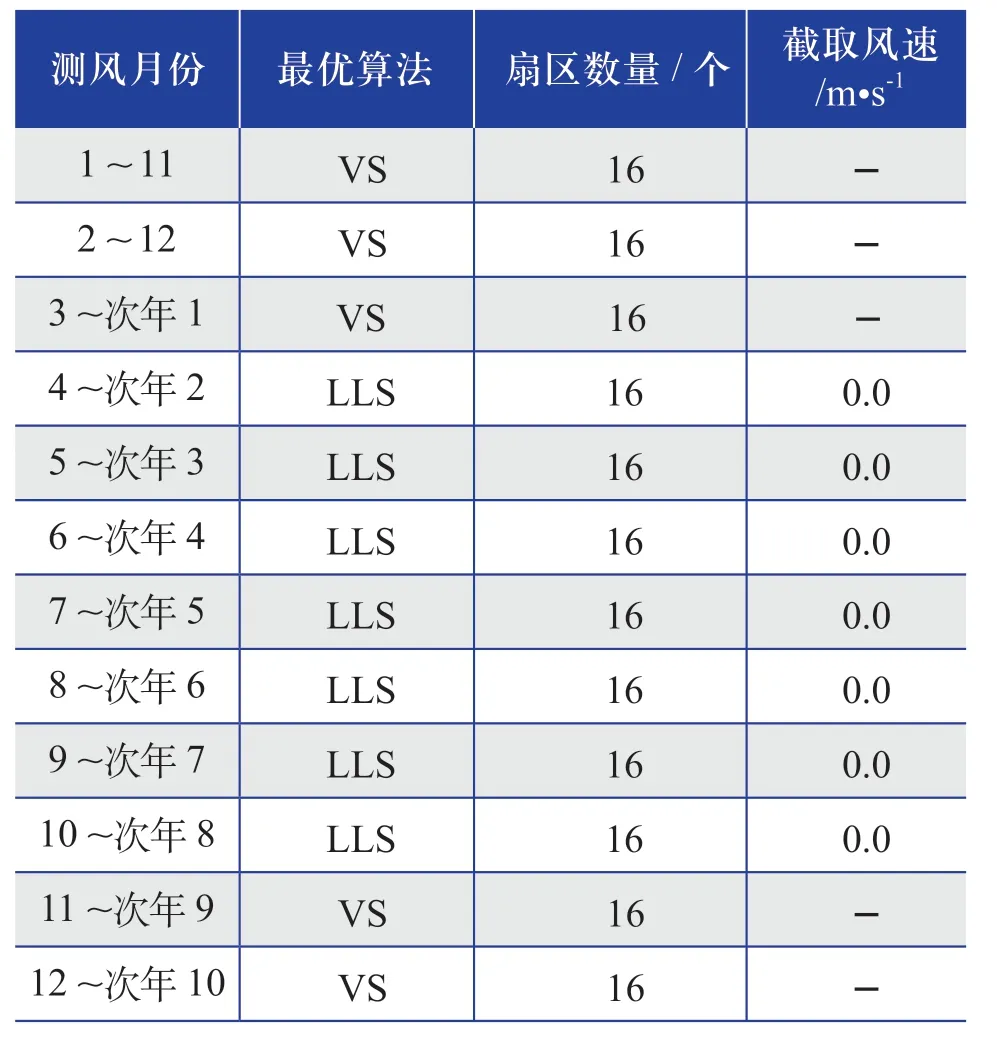
表15 相同测风月份(测风时长为11个月) 最优插补算法的结果Table 15 Results of optimal interpolation algorithm of the same wind measurement month (wind measurement duration is 11 months)

综合表5～表15的推荐插补算法整体结果来看，推荐的插补算法多数为LLS算法，采用“扇区数量为12或16个，截取风速为零”的这种设置。