平面整体冲破式易碎盖结构设计及有限元分析
2021-03-04徐澧明范棋鑫蔡登安南博华周光明
徐澧明,范棋鑫,蔡登安,南博华,周光明
(1.南京航空航天大学机械结构力学及控制国家重点实验室,江苏南京 210016;2.上海航天设备制造总厂有限公司,上海 200245)
0 引言
导弹发射箱盖是导弹发射系统的重要部件,在导弹储运时需在一定的气压内保持气密性,并在导弹发射时需及时开启,确保导弹正常发射。传统的导弹发射箱盖大多为金属盖,其开启方式采用机械开启或爆破开启。其中,机械开启方式存在重量大、开启机械结构复杂、易发生机械故障和开启时间长等缺点,而爆破开启方式存在使用维护成本高、爆炸螺栓爆破时损伤弹头内电子设备等缺点。
随着复合材料的发展,纤维增强复合材料的重量轻、强度高、环境适应性好、可设计性强等优点凸显。其中,连续纤维增强方式在力学性能方面表现出特有的优越性,与短纤维、颗粒、晶须相比,它不但具有高强度还具有高韧性[1]。而环氧树脂基复合材料在成型过程中可选用的固化剂类型多,工艺适应性好,成本较低,便于推广使用,是最常用的先进树脂基复合材料[2]。为克服传统金属发射箱盖的缺点,利用连续纤维增强环氧树脂基复合材料,将发射箱盖设计为既可承受一定范围内气压,又可被特定气压冲破的易碎结构,已经成为国内外导弹发射箱盖的研究热点。
DOANE 等[3]研制了穿透式复合材料易碎盖,在导弹发射时,利用弹头顶破易碎盖预置的薄弱区,使其迅速破碎,确保导弹快速发射。这种易碎盖的设计方案,需充分考虑弹头的抗冲击性能,严格控制易碎盖薄弱区结构的强度,以避免损坏弹头。KAM 等[4]和WU 等[5]研制了一种可控制破坏轨迹的冲破式复合材料易碎盖,该易碎盖利用导弹的高速尾焰冲破,实现快速开启。SHARIFI 等[6]对易碎盖的不同铺层角度([0]6和[0/45]3)、不同几何外形(半球形、椭球形和准球形)进行了讨论,通过有限元分析和试验研究,探究了铺层方式、几何外形对其刚度和强度的影响机理。钱元[7]对整体冲破式复合材料易碎盖进行了结构设计,建立了易碎盖的冲破瞬态动力学数值分析模型,并通过实验验证了其设计方案和数值模型的合理性。曹然[8]提出了分瓣式复合材料易碎盖结构设计方案,对其承压性能、冲破性能进行了有限元分析和试验研究。周光明等[9]提出了一种带薄弱区薄膜盖的设计方案,建立了其理论预测方法,并利用冲破试验对设计方案和理论方法进行了验证。钱元等[10-11]详细研究了易碎盖薄弱区结构及其参数对其性能的影响。CAO等[12]提出了圆形复合材料易碎盖薄弱区结构的参数化设计方法。CAI 等[13]提出了一种圆帽型复合材料易碎盖,其抛出体和法兰利用胶接连接,并通过在内外表面贴纤维布条对薄弱区进行加强。ZHOU等[14]研制了一种可定向抛出分离部分的新型易碎盖。CAI 等[15]针对复合材料易碎盖的破坏机理,提出了基于近似黎曼算法的瞬态动力学模型。
随着导弹发射技术的发展,对导弹盖在轻质和紧凑型结构等方面提出了新需求,因此,亟需展开新型号易碎盖的研制。本文从材料和结构两方面同步设计了一种具有新型薄弱区结构的复合材料易碎盖,并对其承压性能和冲破性能进行了有限元分析。
1 易碎盖结构和材料
本文所设计的易碎盖为圆形平面结构,按各区功能划分可分为3 部分:抛出体、薄弱区和法兰,如图1(a)所示。在导弹存储运输时,易碎盖通过法兰整体固定于导弹发射筒上;在导弹发射时,导弹尾焰使发射筒内的气压迅速增大,引起易碎盖薄弱区结构破坏,抛出体在气体的冲击下抛出,为导弹让出前进通道。
易碎盖采用玻璃纤维增强环氧树脂基复合材料为主要原料,整体由0°/90°双向高强玻璃纤维布以[(0/90)/(±45)]的准各向同性铺层方式循环层叠而成,平均每层的厚度为0.4 mm。对于易碎盖薄弱区结构的制造,首先在预设薄弱区的位置制造所需宽度和深度的凹槽,如图1(b)所示;然后再在凹槽中重新注入环氧树脂胶液,如图1(c)所示,待其固化后将其打磨平整。其中,凹槽的加工深度需为单层板厚度的倍数,以使剩余厚度中的双向高强玻璃纤维布不受损伤,确保薄弱区剩余力学性能的稳定。这种薄弱区制造方式,无需将盖体完全切割开,工艺参数可控,既可以使易碎盖具有更好的气密性能,又可以降低其整体性能的离散性。
另外,在设计制造易碎盖时,可根据易碎盖不同的应用工况,调整易碎盖的铺层厚度、薄弱区凹槽的宽度和深度等设计参数,以使其达到预期的性能指标。平面整体冲破式易碎盖相关尺寸如图2所示。
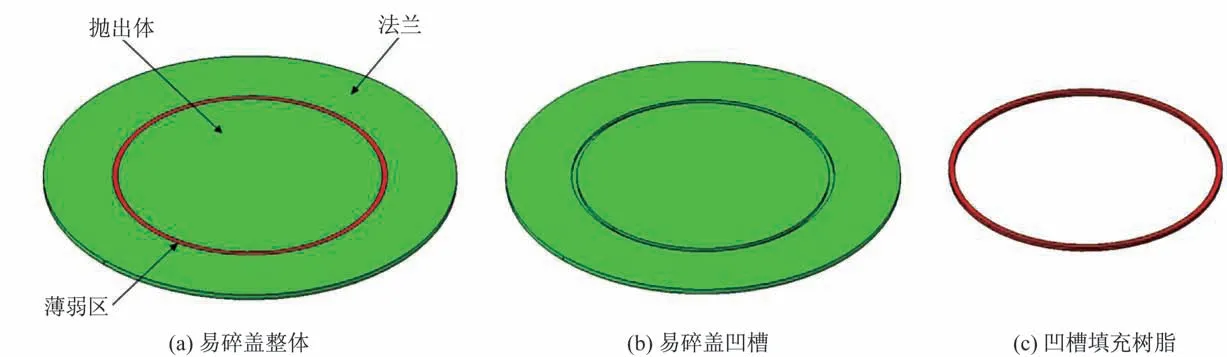
图1 易碎盖构示意图Fig.1 Schematic diagram of the frangible cover structure
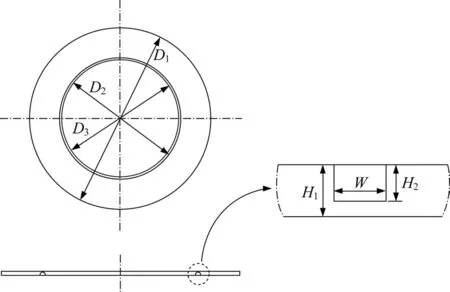
图2 易碎盖尺寸示意图Fig.2 Schematic diagram of the frangible cover dimensions
图2 中:D1为易碎盖法兰的外径;D2为易碎盖法兰的内径;D3为易碎盖抛出体的直径;H1为易碎盖的厚度;H2为凹槽的深度;W为凹槽的宽。其中,W=(D2-D3)/2,本文所设计易碎盖的基础尺寸数据见表1,在后续讨论分析中,其具体的尺寸数据将在此基础上进行变化。

表1 易碎盖尺寸Tab.1 Dimensions of the frangible cover mm
2 易碎盖承压性能分析
2.1 应力和变形分布
在承压工况下,应力和变形分布是考察易碎盖承压性能的重要指标。为研究平面整体冲破式易碎盖设计方案的应力和变形分布规律,将表1 所示尺寸的易碎盖采用C3D8R 实体单元进行离散,在法兰位置施加固支边界条件,对抛出体和薄弱区施加0.1 MPa 的均布载荷,建立承压工况的静态有限元数值分析模型,分析了其应力和变形的分布情况。
易碎盖材料组分中单层板及其树脂的材料性能参数分别见表2 和表3。表2 中:E1、E2、E3为拉伸模量;G12、G23、G13为剪切模量;μ12、μ23、μ13为泊松比;S12、S23、S13为剪切强度;Xt、Yt、Zt分别为x、y、z3 个方向的拉伸强度;Xc、Yc、Zc分别为x、y、z3 个方向的压缩强度;上述符号下标中的1、2、3 分别代表直角坐标系中x、y、z3 个方向。表3 中:E为环氧树脂的弹性模量;μ为环氧树脂的泊松比;Xmt为环氧树脂的拉伸强度。

表2 单层板性能参数Tab.2 Property parameters of the composite laminate

表3 环氧树脂性能参数Tab.3 Property parameters of the epoxy resin
易碎盖有限元模型的应力和变形分布结果如图3 所示。图3(a)为薄弱区凹槽填充树脂的Mises应力分布云图;图3(b)和图3(c)为易碎盖除去凹槽填充树脂部分的Mises 应力分布云图,其中,图3(b)为俯视图,图3(c)为仰视图;图3(d)为易碎盖变形分布云图。
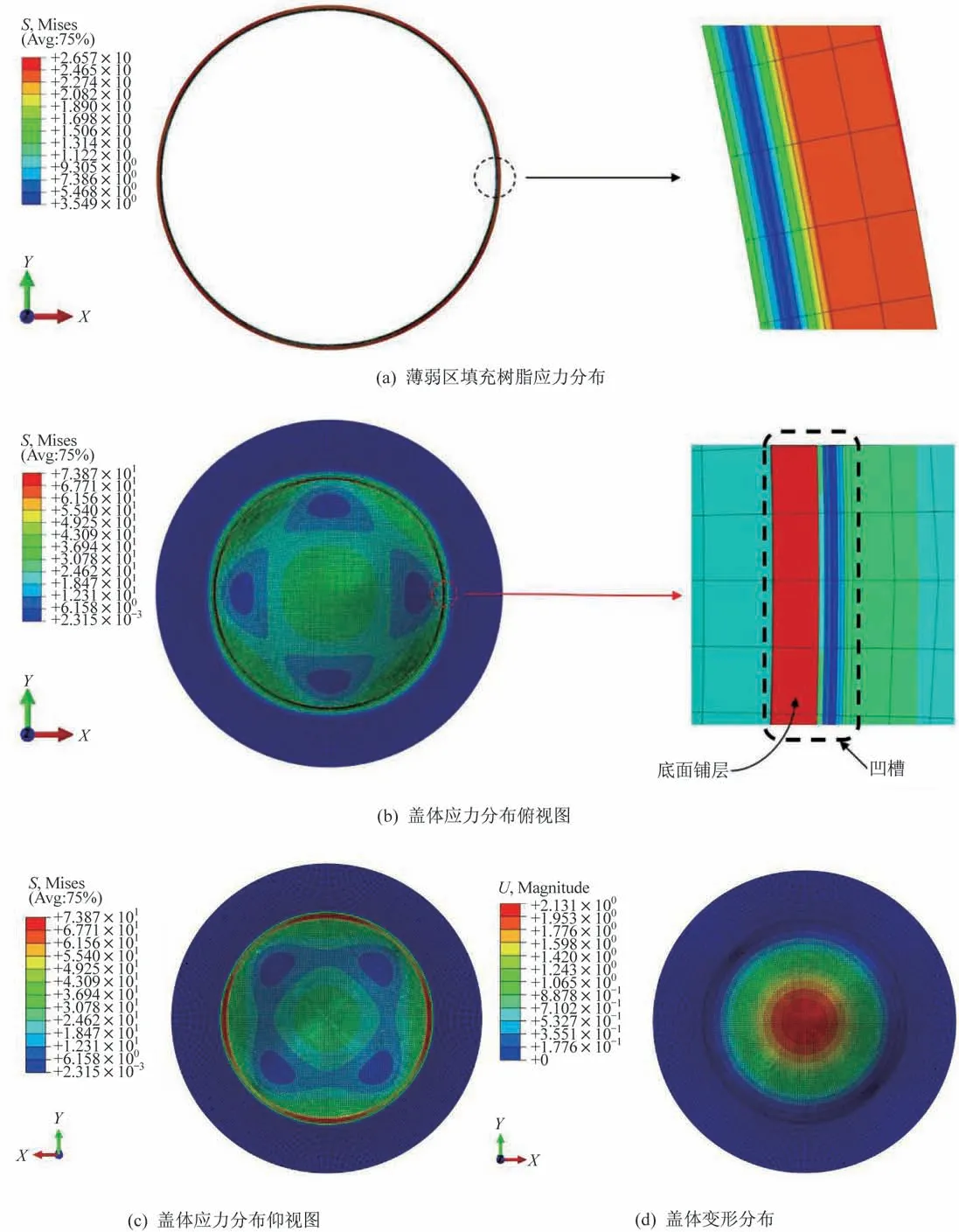
图3 盖体应力和变形分布Fig.3 Distributions of the stress and deformation of the frangible cover
由图3(a)可知,沿厚度方向上,薄弱区填充树脂在中间区域应力最小,在顶面的应力最大,其最大值为26.57 MPa。由图3(b)和图3(c)可知,对易碎盖除去凹槽树脂部分,其应力值较大的区域为薄弱区凹槽底面铺层,最大值为73.87 MPa,大于填充树脂的最大应力值。由图3(d)可知,易碎盖的变形从中心到法兰呈环状分布,其中中心区域位移最大,为2.13 mm。综合可知,整个易碎盖应力最大部分和薄弱区主要承力区域都为凹槽底面铺层。因此,凹槽底面铺层的强度决定了整个易碎盖的强度。
2.2 结构参数对变形的影响
在承压工况下,易碎盖的最大变形是判断设计方案成败的关键指标之一。因此,对影响易碎盖变形的结构参数的讨论至关重要。本节分别对不同盖体厚度(铺层层数)和薄弱区宽度(凹槽宽度)的易碎盖建立了承压工况静态有限元模型,对其最大变形的变化进行了分析。
对于盖体的厚度,在保持凹槽宽度2 mm 和凹槽底部铺层厚度0.4 mm 不变的情况下,讨论了铺层层数为6~12 层的7 种情况,对应的厚度为2.4~4.8 mm。而对于薄弱区宽度,在铺层层数保持10 层和凹槽底部铺层厚度0.4 mm 不变的情况下,凹槽宽度讨论了2、4、6、8 和10 mm 共5 种情况。在所有讨论中,载荷方式均为对薄弱区和抛出体施加0.1 MPa均布压力。易碎盖最大变形随盖体厚度变化的趋势如图4 所示。易碎盖最大变形随薄弱区宽度变化的趋势如图5 所示。
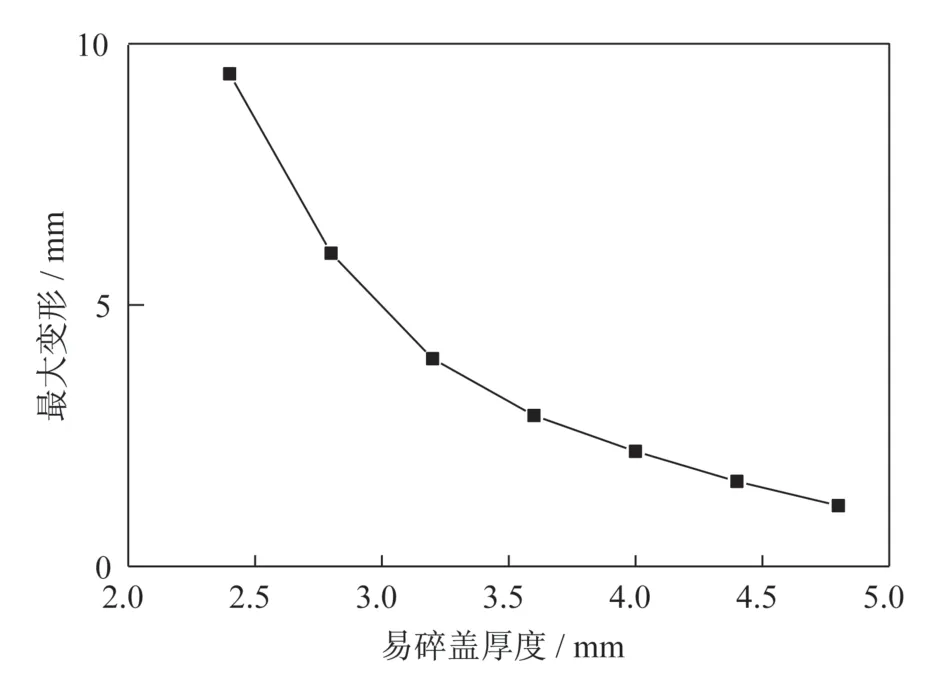
图4 最大变形随厚度变化曲线Fig.4 The curve of the maximum deformation of the frangible cover with the change in its thickness

图5 最大变形随凹槽宽度变化曲线Fig.5 The curve of the maximum deformation of the frangible cover with the change in the groove width
由图4 可知,易碎盖的最大变形随厚度的增加呈现非线性下降趋势,盖体厚度越大,其最大变形减小得越缓慢。当盖体厚度从2.4 mm 增至3.6 mm(铺层从6层增加到9层)时,其最大变形减小了6.5 mm;而当盖体厚度从3.6 mm 增至4.8 mm(铺层从9 层增至12 层)时,其最大变形仅减小了1.7 mm。
由图5 可知,易碎盖最大变形随凹槽宽度的增大呈现非线性增长趋势,但增长速度和增长幅度均较小,凹槽宽度从2 mm 增至10 mm,其最大变形仅增加了0.4 mm。
综合可知:对于本文所述尺寸的易碎盖,盖体的厚度变化对最大变形的影响要明显大于凹槽宽度变化带来的影响,凹槽宽度的变化对易碎盖最大变形的影响十分有限,在盖体厚度不大于3.6 mm(铺层不大于9 层)时,增加铺层层数可明显减小盖体的最大变形;而当盖体厚度大于3.6 mm(铺层大于9 层)后,增加铺层层数对减小盖体最大变形的影响明显减弱。
3 易碎盖冲破性能分析
冲破式易碎盖在能承受一定贮存压力的同时,又需在特定的压力下冲破。易碎盖的冲破性能是判断冲破式易碎盖设计方案成败的关键指标之一。本文基于三维Hashin 失效准则和Von-Mises 失效准则,利用Fortran 语言编写了ABAQUS 有限元软件的UMAT 子程序,对前文中具有不同结构参数的易碎盖建立了渐进损伤有限元模型,对其损伤失效机理进行了探讨。其中,三维Hashin 失效准则用于判断易碎盖的层合复合材料的失效,Von-Mises 失效准则用于判断薄弱区中填充树脂的失效。
3.1 失效准则及刚度退化方案
三维Hashin 失效准则[16]将层合复合材料的失效概括为4 种形式:纤维拉伸失效、纤维压缩失效、纤维束基体拉伸失效和纤维束基体压缩失效。具体的表达形式如下:
纤维拉伸失效(σ11>0):

纤维压缩失效(σ11<0):

基体拉伸失效(σ22+σ33>0):
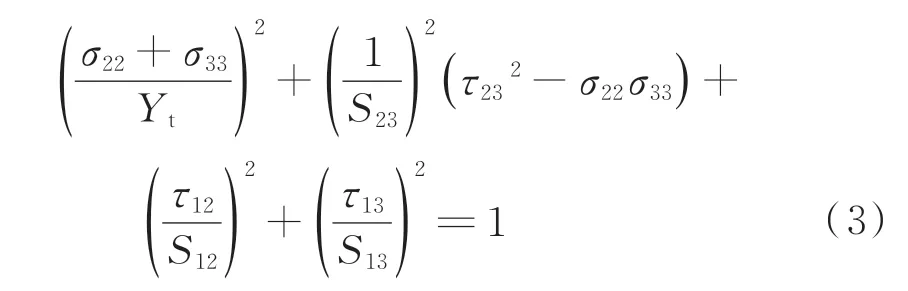
基体压缩失效(σ22+σ33<0):
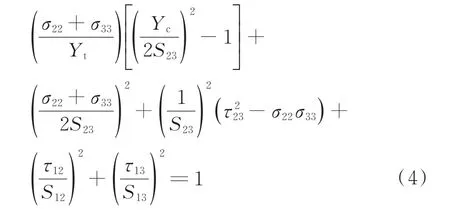
式中:σ11、σ22、σ33、τ12、τ13、τ23为以纤维轴向为1 方向、纤维横向为2 和3 方向的局部直角坐标系下的应力分量。
Von-Mises 失效准则的形式如下:

式中:σx、σy、σz、τxy、τxz、τyz为基体在任意坐标系下的应力分量。
在UMAT 子程序中,失效准则用于判断组分材料是否发生损伤,对于判定为发生损伤的组分,需对其相应单元积分点的弹性参数进行折减退化。针对各向异性材料的损伤特性,不同的损伤类型对应不同的刚度折减方法。
本文采用CAMANHO 等[17]提出的刚度折减方案作为盖体层合复合材料的刚度退化准则,具体的刚度退化系数见表4 所示,其中,刚度符号的上标0表示性能折减前的状态。

表4 刚度退化模型Tab.4 Stiffness degradation model
另外,对于易碎盖薄弱区填充树脂的退化准则为

式中:C为填充树脂的刚度矩阵;λ为刚度折减系数,此处取0.2;上标0 同样代表性能折减前的状态。
3.2 易碎盖损伤失效分析
本节以盖体厚度4 mm、薄弱区凹槽宽度6 mm、凹槽深度3.6 mm 的易碎盖为例,对本文所设计的易碎盖在冲破工况下的渐进损伤过程进行分析。易碎盖从承压状态到损伤破坏过程易碎盖中心的载荷位移曲线如图6 所示。

图6 易碎盖中心载荷位移曲线Fig.6 The displacement curve of the frangible cover center with its load
由图6 可知,易碎盖中心的载荷位移曲线分为线性阶段和非线性阶段,分别对应易碎盖的弹性变形阶段和损伤破坏阶段。当载荷小于0.28 MPa 时,易碎盖未损坏,处于线弹性变形阶段;当载荷达到0.28 MPa 时,载荷位移曲线的斜率开始变小,说明易碎盖的单元发生了刚度折减,易碎盖薄弱区凹槽中的填充树脂开始发生损坏,如图7 所示。当载荷达到0.32 MPa 时,易碎盖薄弱区凹槽底部区域开始发生纤维束基体拉伸失效,如图8 所示,此时载荷位移曲线的斜率进一步减小;当载荷达到0.33 MPa时,易碎盖薄弱区凹槽底部区域开始发生纤维拉伸失效,如图9 所示。
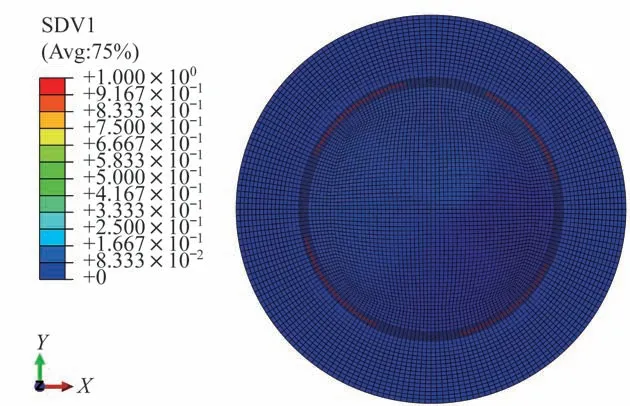
图7 压力0.28 MPa 时易碎盖凹槽树脂失效Fig.7 Resin failure of the frangible cover at the pressure of 0.28 MPa
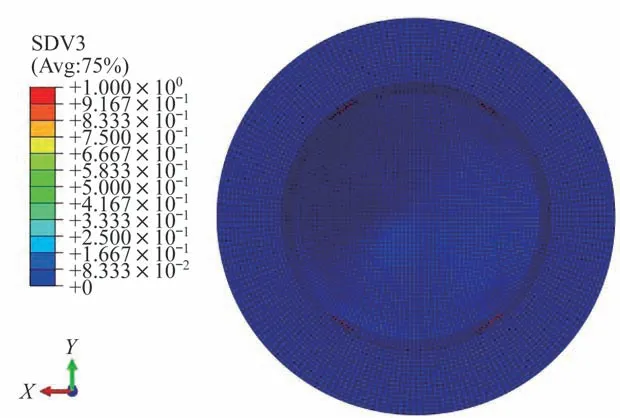
图8 载荷0.32 MPa 时凹槽底部纤维束基体拉伸失效Fig.8 Yarn-matrix tensile failure of the groove bottom at the pressure of 0.32 MPa

图9 载荷0.33 MPa 时凹槽底部纤维拉伸失效Fig.9 Fiber tensile failure of the groove bottom at the pressure of 0.33 MPa
当载荷达到0.35 MPa 时,易碎盖薄弱区凹槽底部铺层多数单元已经失效如图10 和图11 所示,载荷位移曲线趋于平缓,随着位移的增加,载荷并没有明显增长。说明易碎盖失去了承载能力,可认为易碎盖已经冲破,抛出体已与法兰框脱离。
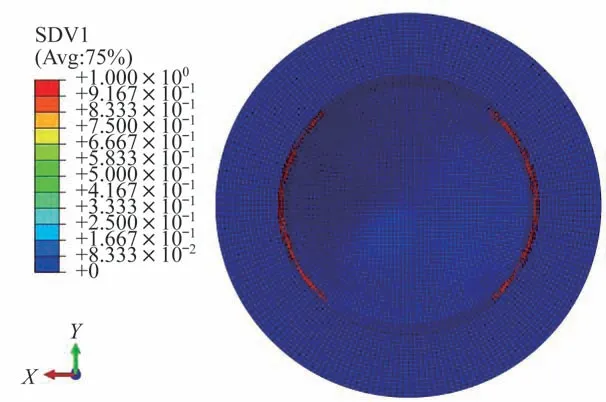
图10 载荷0.35 MPa 时凹槽底部纤维拉伸失效Fig.10 Fiber tensile failure of the groove bottom at the pressure of 0.35 MPa

图11 载荷0.35 MPa 时凹槽底部纤维束基体拉伸失效Fig.11 Yarn-matrix tensile failure of the groove bottom at the pressure of 0.35 MPa
3.3 盖体厚度和凹槽宽度对损伤的影响
本节以表1 所示尺寸的易碎盖为基础,分别分析了盖体厚度和薄弱区凹槽宽度的变化对易碎盖冲破性能的影响。其中,在对盖体厚度进行讨论时,保持凹槽宽度和凹槽底部铺层厚度不变,分别为2 mm 和0.4 mm;而在对薄弱区凹槽宽度进行讨论时,则保持盖体厚度和凹槽底部铺层厚度不变,分别为4 mm 和0.4 mm。不同盖体厚度、不同薄弱区凹槽宽度易碎盖盖体中心的载荷位移曲线如图12 和图13 所示。
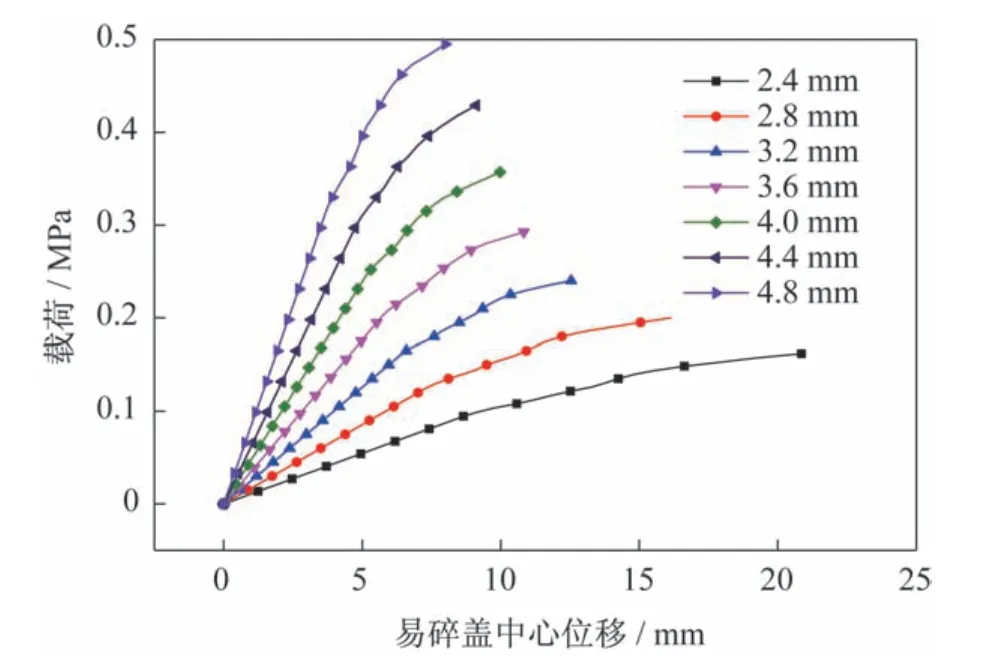
图12 不同厚度易碎盖中心的载荷位移曲线Fig.12 The load-displacement curves of the frangible cover center with different cover thicknesses
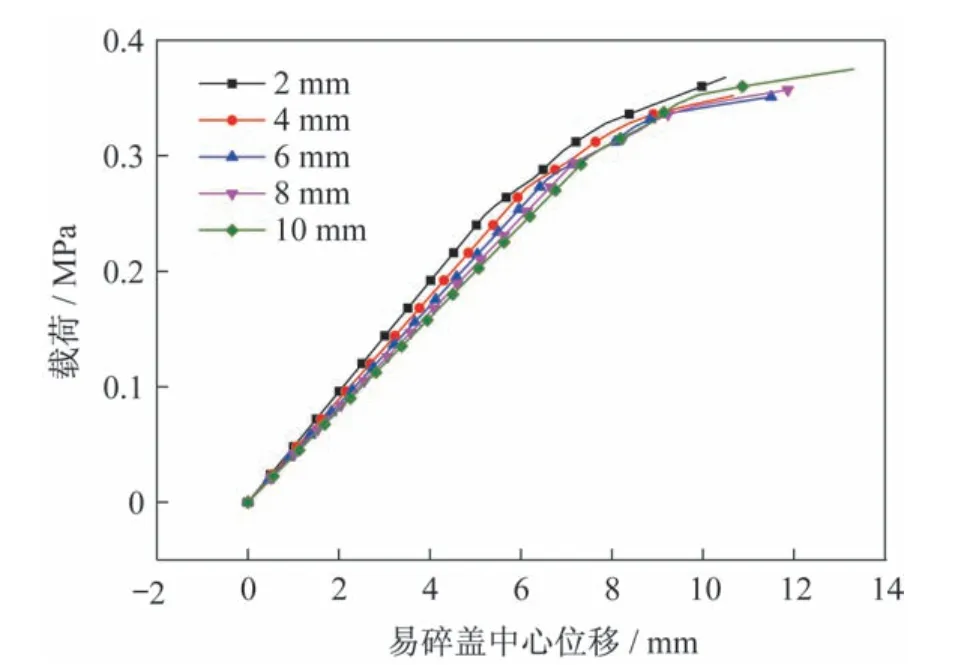
图13 不同凹槽宽度易碎盖中心的载荷位移曲线Fig.13 The load-displacement curves of the frangible cover center with different groove widths
图12 中,列出了 从2.4 mm 到4.8 mm 共7 种 盖体厚度易碎盖中心的载荷位移曲线。由图12 可知,在薄弱区凹槽宽度和凹槽底部铺层厚度不变的情况下,随着盖体厚度的增加,载荷位移曲线线性区域的斜率增大,说明盖体的刚度增大,在相同压力下,盖体中心的变形减小。盖体厚度从2.4 mm(盖体铺层层数6 层)到4.8 mm(盖体铺层层数9 层)对应的冲破压力分别0.16、0.20、0.24、0.29、0.36、0.43和0.50 MPa,盖体厚度增加了100.00%,对应的冲破压力增幅达205.56%,说明盖体厚度的变化,对易碎盖冲破压力有显著的影响。
图13 中,给出了2 mm 到10 mm 共5 种凹槽 宽度易碎盖中心的载荷位移曲线。由图13 可知,随着凹槽宽度的增大,载荷位移曲线线性区域的斜率减小,但减小的幅度很小,说明盖体刚度减小,但减小幅度较小;上述5 种凹槽宽度对应的冲破压力分别为0.37、0.35、0.35、0.36 和0.38 MPa,其变异系数仅为2.60%,说明凹槽宽度的变化对易碎盖冲破压力的变化影响很小。
综上可知,对于本文所述结构和尺寸的易碎盖,盖体厚度的变化对易碎盖的变形及极限承压值影响较大,而薄弱区凹槽宽度的变化对其影响十分有限。因此,对于本文提出的平面整体冲破式易碎盖,在设计和加工时,若想改变其刚度和极限承压能力,应首先考虑调整其铺层厚度。
4 结束语
本文提出了平面整体冲破式易碎盖结构设计方案,并建立了其静态承压有限元模型和渐进损伤有限元模型,分析了其结构参数对其刚度和强度的影响。结果表明,在针对具体技术指标设计易碎盖时,应首先考虑盖体厚度的变化对其承压性能和冲破性能的影响,而其凹槽宽度的变化对其影响很小,可适度增加凹槽的宽度,以便于减小后期加工的难度和误差。本文的有限元分析结果可为进一步试验研究及制备提供技术支持。关于易碎盖直径的变化和薄弱区凹槽底部铺层厚度的变化对其承压和冲破性能的影响并未作出讨论,可待后续深入研究。
