基于改进TOPSIS与哈斯图耦合的水质评价模型
2021-03-03彭琪张宇张强曾开帅唐金平
彭琪 张宇 张强 曾开帅 唐金平


摘 要:将KL散度与TOPSIS结合优化了传统TOPSIS水质评价模型,为了使评价结果直观、可视化,将优化后的TOPSIS模型与哈斯图技术耦合,建立了基于KL散度的TOPSIS与哈斯图耦合的水质评价模型。北京某厂区周边村落地下水水样的实例分析表明,建立的水质评价模型的评价结果与实际情况相符,证明了该评价模型的有效性及合理性;最终评价结果以图的形式展现出来,可视化更强;相对于传统TOPSIS水质评价模型评价结果更精细化,且有利于提高评价结果的精确度。
关键词:KL散度;TOPSIS评价模型;哈斯图;水质评价
中图分类号:X824;TV211.1文献标志码:A
doi:10.3969/j.issn.1000-1379.2021.01.018
引用格式:彭琪,张宇,张强,等.基于改进TOPSIS与哈斯图耦合的水质评价模型[J].人民黄河,2021,43(1):93-96,128.
Model of Water Quality Assessment Based on Improved TOPSIS Coupled with Hasse Diagram
PENG Qi, ZHANG Yu, ZHANG Qiang, ZENG Kaishuai, TANG Jinping
(State Key Laboratory of Geohazard Prevention and Geoenvironment Protection,
Chengdu University of Technology, Chengdu 610059, China)
Abstract: The traditional TOPSIS water quality evaluation model was optimized by combining KL (Kullback-Leibler) divergence and TOPSIS. In order to make the evaluation results intuitive and visual, the optimized TOPSIS model was coupled with the Hasplot technology and a coupling based on KL divergence and TOPSIS established water quality evaluation model. An example analysis of groundwater samples from a village around a plant in Beijing shows that the evaluation results of the established water quality evaluation model are consistent with the actual situation, proving the validity and rationality of the evaluation model; the final evaluation results are displayed in the form of a graph and visualized stronger; Compared with the traditional TOPSIS water quality evaluation model, the evaluation results are more refined and it is helpful to improve the accuracy of the evaluation results.
Key words: Kullback-Leibler divergence; TOPSIS evaluation model; Hasse Diagram; water quality evaluation
隨着我国城市化与工业化进程的不断加快,水环境问题日益突出,已成为制约社会经济发展的重要因素,而水质评价是水环境问题研究的基础,客观有效的水质评价对水资源的开发利用及城市的发展具有重大意义,因此建立合理有效的水质评价模型是非常必要的。常用的水质评价方法有单因子评价法、F值评价法、层次分析法、模糊综合评价法、人工神经网络法、灰色关联评价法、TOPSIS评价法[1-7]等。在信息论中,KL散度又称为相对熵,用于衡量给定任意分布偏离真实分布的程度,其取值为0~∞,KL散度越小,真实分布与近似分布之间的匹配程度越好[8-9]。欧氏距离又称为欧几里得度量,用于衡量多维空间中两点间的绝对距离,距离越短代表相似度越好。笔者利用KL散度的相似度概念代替传统TOPSIS模型中欧氏距离的相似度概念,以此优化TOPSIS评价模型,提升水质评价结果的精确性。为了使评价结果直观、可视化,将优化后的TOPSIS模型与哈斯图技术耦合,结合各自优点,建立基于KL散度的TOPSIS与哈斯图耦合的水质评价模型。
1 传统TOPSIS评价模型
TOPSIS评价法亦称理想解法,主要依靠样品的理想方案和负理想方案进行排序评级,是一种有效的多指标评价方法。TOPSIS评价法步骤[10]:①构建评价数据矩阵A=(aij)mn,经无量纲化处理得到B=(bij)mn;②构建加权规范化矩阵C=(cij)mn,并确定样品的理想方案S+和负理想方案S-;③计算各样品与理想方案、负理想方案的欧氏距离d+、d-;④计算各样品与理想方案的相对贴合度T,按T值大小排序评级。
传统TOPSIS水质评价模型中采用的是线性欧氏距离,由于该测度不考虑评价指标间的差异,精确度相对较差,而指标间差异大小直接影响评价结果的准确性,因此传统TOPSIS水质评价模型的稳定性有所欠缺。
2 建立改进的TOPSIS评价模型
建立基于KL散度的TOPSIS与哈斯图耦合的水质评价模型,具体建模步骤如下。
(1)数据处理。根据评价区域实际情况,将采集的m个样品,合理选取n个评价指标,构成评价数据矩阵A=(aij)mn。为了后续数据处理方便,将矩阵A无量纲化处理后得到矩阵B=(bij)mn,无量纲化处理公式为
bij=aija1j2+a2j2+…+amj2 (1)
(2)构建加权规范化矩阵。利用熵权法计算各评价指标的权重,得到各指标权重向量W=(w1,w2,…,wn)T ,并构建加权规范化矩阵C=(cij)mn=WB。
(3)确定样品的理想方案S+和负理想方案S-。水质最优的一组水样为理想方案,水质最差的一组水样为负理想方案,结合水质评价的特点,其理想方案和负理想方案分别为
S+={c+1,c+2,…,c+m},c+m=min(cj)(2)
S-={c-1,c-2,…,c-m},c-m=max(cj) (3)
(4)分别确定S+和S-的KL散度矩阵K+、K-。通过式(4)、式(5)获得理想方案S+的KL散度矩阵K+=(k+ij)mn和负理想方案S-的KL散度矩阵K-=(k-ij)mn。
k+ij=c+jlnc+jcij+(1-c+j)ln1-c+j1-cij (4)
k-ij=c-jlnc-jcij+(1-c-j)ln1-c-j1-cij(5)
(5)构建等级决策矩阵。结合文献[11]的研究成果,将KL散度矩阵K+、K-,按各个指标的权重大小排序,在各评价指标的权重满足ω11>ω12>…>ω1n条件下,经式(6)、式(7)换算获得样品等级决策矩阵P=(pij)mn、Q=(qij)mn。
pij=∑nj=1k+ij(6)
qij=∑nj=1k-ij(7)
(6)建立比较关系矩阵。在矩阵P、Q中每一行均代表一个样品,对矩阵P、Q中任意两行x、y进行比较:①矩阵P中x行任意一个数均小于或等于y行中任意一个数;②矩阵Q中x行任意一个数均大于或等于y行中任意一个数。当①、②同时满足时,记作Ps(x)≥Ps(y),此时rxy=1,否则rxy=0,比较关系矩阵R为
R=(rxy)mm(8)
(7)获得HASSE矩阵,绘制哈斯图。将比较关系矩阵参照文献[12]处理过程,经式(9)进行布尔运算,获得无回路的HASSE矩阵HR,利用带有标识的圆将存在覆盖关系的样品用线连接起来[13],绘制可视化哈斯图。
HR=R-(R-I)2-I(9)
式中:I为单位矩阵。
(8)分析哈斯图,获得评价结果。
3 实例分析
利用16组取自北京某厂区周边村落的地下水水样,将Cl-、SO2-4、NO-3、TDS、Fe3+、Zn、Mn、NO-2作为评价指标,运用上述水质评价模型对其进行水质评价,并将评价结果与传统TOPSIS水质评价模型评价结果进行对比,以验证评价模型的合理性。
3.1 数据处理
首先采用式(1)将评价数据矩阵A=(aij)mn转化为无量纲化矩阵B=(bij)mn,見表1,其中B1~B4为依据《地下水质量标准》(GB/T 14848—2017)构造的水质分级临界水样,这4组临界水样可将水质划分为5个级别,将其加入到待评价水样中共同参与评价的目的是给待评价水样的水质进行定级。然后运用熵权法,获得各个评价指标权重信息(见表2),并构建加权规范化矩阵C=(cij)mn。
3.2 确定理想方案S+和负理想方案S-
根据加权规范化矩阵C=(cij)mn,利用式(2)、式(3)确定样品理想方案和负理想方案,见表3。再根据式(4)、式(5)确定S+和S-的KL散度矩阵K+、K-(表略)。
3.3 确定样品理想等级决策矩阵P和样品负理想等级决策矩阵Q
根据式(6)、式(7)换算获得样品理想等级决策矩阵P和样品负理想等级决策矩阵Q,见表4、表5。
3.4 建立比较关系矩阵
根据式(8)建立比较关系矩阵R(见表6),再由式(9)经布尔运算获得HASSE矩阵HR(表略)。
3.5 绘制哈斯图,分析评价结果
根据HASSE矩阵,绘制水质评价哈斯图,见图1。由图1可知,20个水样分为了6个层级,第一层级水样为B4,第二层级水样为B3、X16、X8,第三层级水样为B2、X11、X10、X12,第四层级水样为X9、X6、X1、X14,第五层级水样为B1、X2、X13、X5、X15,第六层级水样为X7、X3、X4。依据设定的4组(B1~B4)水质分级临界水样,参照《地下水质量标准》(GB/T 14848—2017)Ⅰ类水为(0,B1)、Ⅱ类水为[B1,B2)、Ⅲ类水为[B2,B3)、Ⅳ类水为[B3,B4)、Ⅴ类水为[B4,+∞)的分级原则,16个水样的水质评价结果见表7。根据表7,该厂区周边村落地下水水质属于中等偏上水平。
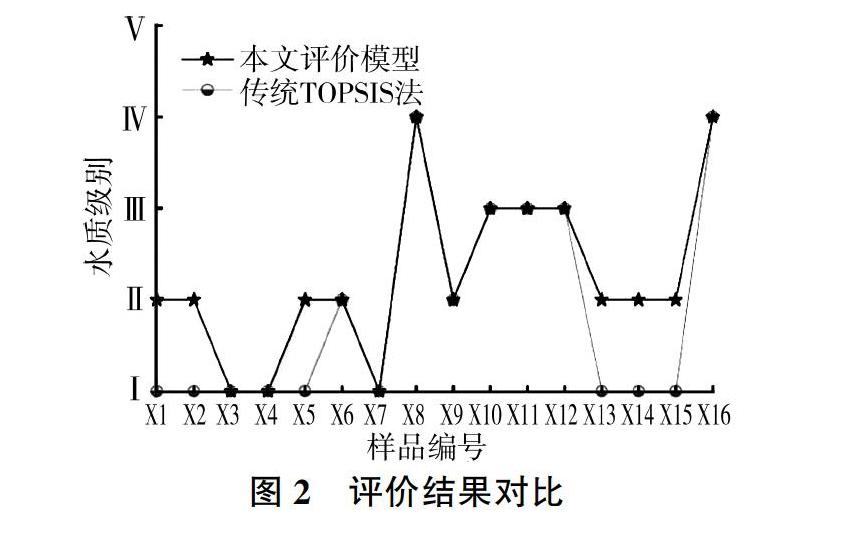
3.6 对比分析
将基于KL散度的TOPSIS与哈斯图耦合模型评价结果与传统TOPSIS水质评价模型评价结果进行对比,见图2。经比较,两种方法评价结果大体相同,验证了该评价模型的可行性。从X1~X5水样评价结果可以看出,传统TOPSIS评价模型将其归为同一类水质级别,而基于KL散度的TOPSIS与哈斯图耦合评价模型考虑了指标间的细微差异,并将其进一步细分为了两类,由此可见,传统的TOPSIS评价模型中的欧氏距离将水样不同指标间的差别等同看待,没有考虑水样指标间差异对整体评价结果的影响,因此采用统计独立性最佳的KL散度来改进TOPSIS法有利于提高评价结果的精确度。
4 结 语
将KL散度与TOPSIS法相结合,建立了基于KL散度的TOPSIS与哈斯图耦合的水质评价模型,该评价模型结合了KL散度、TOPSIS法和哈斯图各自的优点,实用性和应用性更强。北京某厂区周边村落地下水水样的实例分析表明,基于KL散度的TOPSIS与哈斯图耦合的水质评价模型评价结果与实际情况相符,证明了该评价模型的有效性及合理性;最终评价结果以图的形式展现出来,可视化更强;相对于传统TOPSIS水质评价模型评价结果更精细化,且有利于提高评价结果的精确度。但哈斯图的引入使得该模型的计算相较于传统TOPSIS评价模型略微复杂。在实例应用中,受限于样品数量,未能更清晰展示出用KL散度替代欧氏距离改进的TOPSIS评价模型与传统TOPSIS评价模型评价结果的差异性及优越性。
参考文献:
[1] 刘诚.不同评价方法在阿克苏市地下水水质评价中的应用分析[J].节水灌溉,2019(4):66-71.
[2] 张德彬,刘国东,王亮,等.基于博弈论组合赋权的TOPSIS模型在地下水水质评价中的应用[J].长江科学院院报,2018,35(7):46-50,62.
[3] 艾亚迪,魏传江,李丽琴,等.地下水质评价方法对比:以偃师市为例[J].节水灌溉,2018(11):77-80.
[4] 宛恒.基于BP神经网络-模糊数学串联模型的科左中旗地下水质量评价[D].呼和浩特:内蒙古农业大学,2018:24-50.
[5] 吴先明,蔡海滨,邓鹏.基于灰色关联度的改进TOPSIS模型在水质评价中的应用[J].三峡大学学报(自然科学版),2018,40(2):24-28.
[6] 张岩祥,肖长来,刘泓志,等.模糊综合评价法和层次分析法在白城市水质评价中的应用[J].节水灌溉,2015(3):31-34.
[7] 梁小俊,张庆庆,许月萍,等.层次分析法-灰关联分析法在京杭运河杭州段水质综合评价中的应用[J].武汉大学学报(工学版),2011,44(3):312-316,325.
[8] DHILLON I S, MALLELA S, KUMAR R. A Divisive Infomation-Theoretic Feature Clustering Algorithm for Text Classification[J]. Joumal of Machine Learning Research, 2003(3): 1265-1287.
[9] 宁宝权,谢军,陕振沛.基于相对熵和VIKOR的多属性决策排序方法[J].数学的实践与认识,2019,49(7):35-45.
[10] 张先起,梁川,刘慧卿.基于熵权的改进TOPSIS法在水质评价中的应用[J].哈尔滨工业大学学报,2007(10):1670-1672.
[11] 岳立柱,李良琼.应用偏序集表示权重难以获知的TOPSIS模型[J].模糊系统与数学,2017,31(4):167-174.
[12] 范懿.一个有关哈斯图的解析方法[J].上海第二工业大学学报,2003(1):17-22.
[13] VOIGT K, BRUGGEMANN R, PUDENZ S. A Multi-Criteria Evaluation of Environmental Databases Using the Hasse Diagram Technique (ProRank) Software[J]. Environmental Modelling & Software,2006,21:1587-1597.
【責任编辑 吕艳梅】
