气候和下垫面要素对泾河流域径流变化的影响
2021-03-03刘洪波菅浩然
刘洪波 菅浩然


摘 要:定量評估河川径流的变异规律,开展其归因诊断分析是变化环境下制定应对策略与合理利用水资源的基础。以水资源匮乏的泾河流域为例,首先,采用3种潜在蒸发计算方法(Penman-Monteith方法、Priestley-Taylor方法和Hargreaves-Samani方法)评估径流对气象因素和下垫面因素的敏感性;其次,采用Bayesian突变检验方法识别径流序列的突变年份,以此将气候状态划分为天然期和变化期;最后,采用Budyko-Fu公式定量评估气候变化和人类活动在不同时段对径流改变量的贡献程度。结果表明:不同潜在蒸发计算方法得到的年潜在蒸发量之间差异显著,仅考虑气温和太阳辐射的Hargreaves-Samani方法不确定性影响最大;随着潜在蒸发量的增大,气象因子的弹性系数逐渐减小,而下垫面因子的弹性系数却显著增大;不同时段气候变化和人类活动对径流减小的贡献程度不同,气候变化和人类活动对径流减少的贡献分别为80%和20%左右。
关键词:潜在蒸发量;径流变化归因;Budyko假设;泾河流域
中图分类号:TV213.9文献标志码:A
doi:10.3969/j.issn.1000-1379.2021.01.005
引用格式:刘洪波,菅浩然.气候和下垫面要素对泾河流域径流变化的影响[J].人民黄河,2021,43(1):22-28.
Impacts of Climate and Underlying Surface Factors on Runoff Variation in Jinghe River Basin
LIU Hongbo, JIAN Haoran
(Yellow River Conservancy Technical Institute, Kaifeng 475004, China)
Abstract:Quantitative assessment of the variation law of river runoff and the analysis of its attribution diagnosis are the basis for formulating coping strategies and rational utilization of water resources in a changing environment. This article took the Jinghe River basin as an example, first, the Bayesian mutation test method was used to identify the location of the abrupt change point of runoff, so as to define the climate state as the natural period and the changing period; secondly, three potential evaporation calculation methods (Penman-Monteith method, Priestley-Taylor method and Hargreaves-Samani method) were used to compare and evaluate the difference in sensitivity of runoff to meteorological factors and underlying surface factors; finally, the Budyko-Fu formula was used to quantitatively evaluate the contribution of climate change and human activities to runoff change at different periods. The results show that the annual potential evaporation amount obtained by different potential evaporation calculation methods is significantly different, and the uncertainty of the Hargreaves-Samani method, which only considers the temperature, has the greatest impact; as the potential evaporation increases, the elastic coefficient of meteorological factors gradually decreases, while the elastic coefficient of the underlying surface factor increases significantly; the contribution of climate change and human activities to the reduction of runoff in different periods is different, the contribution of climate change and human activities to the reduction of runoff is about 80% and 20% respectively. The research results are of guiding significance for the scientific and rational development of water resources development and utilization in river basins.
Key words: potential evaporation; attribution of runoff changes; Budyko hypothesis; Jinghe River basin
全球变暖和高强度下垫面活动共同导致区域水循环过程发生改变,其中河川径流变化尤为突出[1-2]。识别并分离气候因子和下垫面因子对河川径流的影响,对深入认知区域水资源的丰枯状态和科学地开展水资源管理规划具有实际意义。
近年来,国内外学者针对流域径流变化归因开展了大量研究[3-4]。总的来说,在分离气候变化和下垫面影响过程中,多采用水文模型方法和基于水热耦合模型的Budyko假设方法。例如,王国庆等[5]采用RCCC-WBM水量平衡模型,以我国七大江河的代表性区域为例,定量評估了不同气象要素对径流变化的影响;刘绿柳等[6]以伊洛河流域为例,通过固定基准期模型参数不变,利用1985—2015年气象数据驱动SWAT模型,获取该时段的天然径流量,通过对比模拟径流量与实测径流量探究了气候变化和人类活动对径流的影响;周帅等[7]以黄河源区为例,采用5种典型的Budyko假设公式,量化评估了气候变化和人类活动与径流的响应关系;杨大文等[8]基于水热耦合平衡方程厘清了黄河流域径流变化的主要原因,指出径流的气候弹性和下垫面弹性基本一致,黄土高原地区的水文过程对气候和下垫面变化更加敏感。虽然水文模型可以模拟流域下垫面变化对径流的影响量,但考虑到模型结构的复杂性、不确定性,其径流变化定量分析备受质疑。综合来看,Budyko方法是分离气候要素和下垫面要素对径流影响的可靠评估方法。此外,弹性系数法因计算简单、结果可靠,被广泛应用于Budyko公式定量评估中,但黄斌斌等[9]研究指出,弹性系数法中的潜在蒸发量很难确定。这也导致学者们采用不同的潜在蒸发量计算方法作为Budyko公式的输入,用于分离气候因子和下垫面因子对径流改变量的贡献程度,如常斐杨等[10]采用Penman公式,石清等[11]采用改进的Hargreaves公式,王国庆等[5]采用Penman-Monteith公式。不同的潜在蒸发量计算方法考虑的气象输入要素不同,可能会导致流域径流变化分析结果“失真”,但针对该方面的研究甚少。
笔者以泾河流域为例,首先,分别采用Penman-Monteith公式、Priestley-Taylor公式和Hargreaves-Samani公式计算流域内及周边27个气象站点的日潜在蒸发量,基于ArcGIS平台,采用泰森多边形法计算流域的面潜在蒸发量,并探究了流域蒸发的时空变化特征;其次,采用贝叶斯(Bayesian)突变检验方法识别流域控制站张家山水文站径流序列的突变年份,并划定不同气候状态变化时段;最后,基于Budyko-Fu公式,采用弹性系数法定量评估不同潜在蒸发量计算方法下气候要素和下垫面要素对径流改变的贡献程度。
1 流域概况及数据来源
泾河流域地处黄河中游,是渭河的第一大支流,干流全长455.10 km,流域面积为4.54万km2,横跨甘肃、陕西和宁夏三省(区)。根据下垫面情况可将流域分为西南部山地林区、东南部山地河川区、中部黄土塬区和残塬区、北部黄土丘陵区。流域属典型的温带大陆性气候区,地处半湿润气候向半干旱气候的过渡区,多年平均气温为8.0 ℃,1970—2016年多年平均降水量为508 mm。流域内长期以来水土流失严重,生态环境脆弱[10,12]。
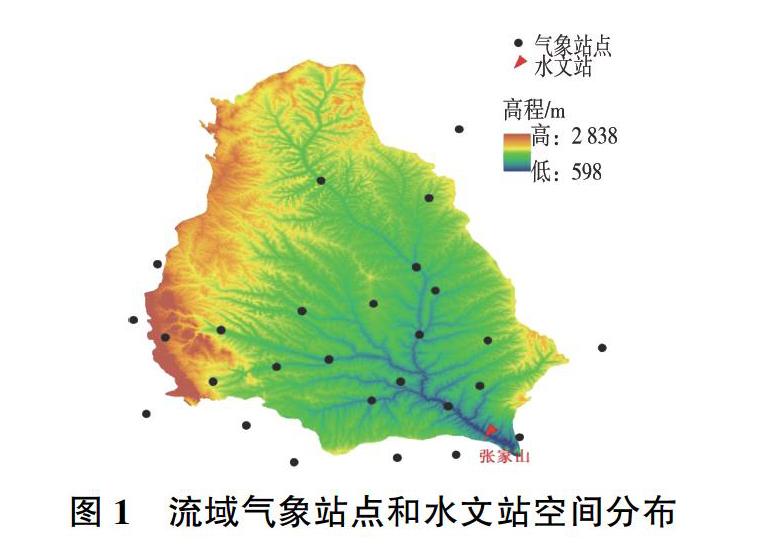
采用流域内及周边27个国家基准气象站和一般气象站点1970—2016年共47 a逐日平均降水量、平均风速、相对湿度、日照时数、平均气温等气象数据,以及同期张家山水文站逐日观测资料。气象数据来源于资源环境数据云平台,水文数据来源于黄河流域水文年鉴。流域气象站点和水文站分布如图1所示。
2 研究方法
2.1 Penman-Monteith公式
采用1998年世界粮农组织(FAO)推荐的Penman-Monteith模型计算潜在蒸发量[7],其公式为
ET0=0.408Δ(Rn-G)+γ900T+273U2(es-ea)Δ+γ(1+0.34U2)(1)
式中:ET0为潜在蒸发量,mm;Δ为饱和水汽压与温度的斜率,kPa/℃;G为土壤热通量,MJ/(m·d);Rn为作物的表面净辐射量,MJ/(m·d);T为平均温度,℃;γ为湿度计常数,kPa/℃;U2为距地面2 m处风速,m/s;es为空气饱和水汽压,kPa;ea为空气实际水汽压,kPa。
2.2 Priestley-Taylor公式
Priestley-Taylor公式为Priestley和Taylor[13]于1972年对Penman公式的修正公式,通过引进常数,给出了在无平流条件下的蒸发计算模型[14],其计算公式为
ET0=αΔΔ+γ(Rn-G)(2)
式中:α为Priestley-Taylor常数,α=1.26。
2.3 Hargreaves-Samani公式
Hargreaves-Samani公式由Hargreaves和Samani提出,以温度和太阳辐射要素为输入[15],其计算公式为
ET0=C0(Tmax+Tmin2+17.8)(Tmax-Tmin)0.5Rn(3)
式中:Tmax和Tmin分别为每日最高气温和最低气温,℃;C0为转化常数,本文取C0=0.002 3。
2.4 贝叶斯(Bayesian)突变检验方法
贝叶斯(Bayesian)突变检验方法[16]基本假定:设序列x(t)在t时刻前后发生了统计性变化,t时刻前后服从的分布密度函数分别为
x1,i→N(μ1,σ21)(i=1,2,…,t)x2,i→N(μ2,σ22)(i=t+1,t+2,…,n)(4)
利用贝叶斯定理和序列值R={Rt , Rt+1}推导出参数μ1和μ2的后验分布,其后验分布为
μ1|x1i→N(μ1,σ21),μ1=(nμ1+∑ti=1Ri)/(n+t)σ21=σ2/(n+t),n=σ2/σ2u(5)
给定特定的水文序列,μ1和μ2发生的联合分布密度函数为
x(R|t,μ1,μ2)=∏ti=11σ2πexp(-ri-μ12σ2)×
∏ni=t+11σ2πexp(-ri-μ22σ2) (6)
采用贝叶斯法则诊断出突变点发生位置的后验分布密度函数:
x(t|R,μ1,μ2)=x(t|R,μ1,μ2)x(t)∑ni=1x(R|i,μ1,μ2)x(t)(7)
式中:μ1和σ1分别为突变前序列对应的均值和方差;μ2和σ2分别为突变后序列对应的均值和方差;R为计算所采用的水文序列(径流);x(t)为位置t的先验分布,一般假定为均匀分布。
突变点的后验发生概率期望值为
x(t|R)=x(t|R,μ1,μ2)x(t)dμ1dμ2(8)
最后依据不同位置的概率最大值,确定水文序列的变异点。
2.5 Budyko-Fu假设公式
1974年著名的气象水文学家Budyko在对全球水量和能量平衡进行分析时发现,蒸发量依赖于降水量和蒸发能力的平衡状态[7],并由此提出了满足边界条件的一般性方程
EP=f(ET0P)=f(X)(9)
式中:E、P、ET0和X分别为流域的多年平均实际蒸发量、多年平均降水量、多年平均潜在蒸发量和干燥指数(潜在蒸发量与降水量之比)。
Budyko-Fu假设平衡方程可以表示为
EP=1+ET0P-[1+(ET0P)ω]1ω(10)
对于一个闭合的流域,多年土壤蓄水量的变化量可以忽略不计,则径流量可以表示为R=f(P,ET0,ω)。徑流的变化可以表示为以下全微分形式:
dRR=εPdPP+εET0dET0ET0+εωdωω(11)
式中:εP、εET0和εω分别为径流对降水、潜在蒸发和下垫面因子的敏感性系数,即弹性系数。
2.6 径流变化归因分析
根据径流突变点位置,可将研究时段划分为两部分(天然期和变化期),天然期的多年平均径流深为R1,变化期的多年平均径流深为R2,变化期径流的变化量可用两个时期的多年平均径流深差值表示[8]:
ΔR=R2-R1(12)
径流的改变可归因于气象要素的变化和流域下垫面特征的变化,其中,气象要素变化又可进一步细化为降水的增加或减少导致的径流变化(ΔRp)和潜在蒸发量的变化导致的径流变化(ΔRET0)。本文假定流域的下垫面要素发生变化导致的径流变化为ΔRω。
根据径流的气候弹性系数(εP和εET0)和下垫面系数(εω),可以分别估算出降水因子、潜在蒸发因子和下垫面因子变化导致的径流变化,计算公式分别为
ΔRP=εPRPΔP
ΔRET0=εET0RET0ΔET0
ΔRω=εωRωΔω(13)
式中:ΔP、ΔET0和Δω分别为天然期与变化期的多年平均降水量的差值、多年平均潜在蒸发量的差值和下垫面参数的差值;ΔRP、ΔRET0和ΔRω分别为降水变化引起的径流变化、潜在蒸发变化引起的径流变化和下垫面变化引起的径流变化。
3 结果与分析
3.1 流域径流序列突变性和趋势性分析
图2为流域控制站张家山水文站1970—2016年径流序列的突变性和趋势性检验结果。由图2(a)可以看出,张家山水文站年径流于1992年后验概率最大,其值为0.032,意味着该年份径流发生了统计性突变;由图2(b)可以看出,1992年之前年均流量以0.80 m3/(s·a)的速率微弱增大,但1992年之后年均流量以7.90m3/(s·a)的速率显著减小(从趋势线可以看出)。因此,采用科学合理的方法厘清突变年之后径流变化的原因,对流域未来水资源规划具有指导意义。
3.2 不同算法潜在蒸发量时空分布结果
图3和图4分别为3种潜在蒸发计算方法(Penman-Monteith公式、Priestley-Taylor公式和Hargreaves-Samani公式,分别简称为P-M、P-T和H-S公式)得到的泾河流域年平均潜在蒸发量及时空分布。由图3可以看出,不同潜在蒸发计算方法得到的年平均潜在蒸发量在量级上差异显著,H-S公式得到的潜在蒸发量最大,P-T公式次之,P-M公式最小,计算的1970—2016年多年平均潜在蒸发量分别为1 160.51、900.35、720.99 mm;在变化幅度上,H-S公式得到的年潜在蒸发量序列在年内变幅最大,而P-T和P-M公式的变幅较小,这意味着仅考虑气温和太阳辐射要素的H-S公式在评估年潜在蒸发量时存在较大的不确定性,而考虑气温、湿度以及辐射等要素的P-T和P-M公式的不确定性较小;此外,H-S公式得到的1970—2016年多年平均潜在蒸发量分别是P-M公式和P-T公式得到的多年平均潜在蒸发量的1.61倍和1.25倍,该结论与Liu等[17]和张晓琳等[18]研究发现的不同蒸发计算方法评估的潜在蒸发量变化差异基本一致,这表明采用不同的潜在蒸发计算方法可能导致流域的水热耦合平衡关系发生改变。
分析图4可以得出,P-M和P-T公式得到的多年平均潜在蒸发量在空间分布上差异较小,整体呈现出由西南至东北逐渐递减的趋势,但局部区域存在差异;H-S公式得到的多年平均潜在蒸发量在流域南部和北部较高,而在西部和东部较低,这归因于流域地处半干旱、半湿润气候带,受季节气候影响明显,潜在蒸发量不仅与温度有关,与局地风速、空气湿度等息息相关,流域北部和南部海拔差异较大,风速变化明显,该结论也进一步揭示了H-S公式在年潜在蒸发量评估上不确定性较大。
4 结 论
以泾河流域为例,首先采用贝叶斯(Bayesian)突变检验方法诊断出流域控制站张家山水文站1970—2016年径流序列的突变位置,并以此将流域气候状态划分为天然期和变化期;其次,对比分析3种潜在蒸发量计算方法(Penman-Monteith公式、Priestley-Taylor公式和Hargreaves-Samani公式)得出的泾河流域潜在蒸发量的时空分布差异;最后,采用典型Budyko-Fu假设公式探究了气候变化和下垫面因子在不同时段对泾河流域径流减少的贡献程度。
(1)贝叶斯突变检验结果表明,泾河流域径流量在1992年发生了突变,1992年之前年均流量以0.80 m3/(s·a)的速率微弱增大,但1992年之后年均流量以7.90 m3/(s·a)的速率显著减小。
(2)不同潜在蒸发量计算方法得到的年潜在蒸发量差异显著,考虑太阳辐射、地面净辐射、风速等的Penman-Monteith方法和Priestley-Taylor方法,其年潜在蒸发量在时空上变化趋势基本一致,而仅考虑气温和太阳辐射的Hargreaves-Samani方法与其他方法结果差异较大,具有较大的不确定性。
(3)不同潜在蒸发量计算方法得出的径流对气象因子和下垫面因子的敏感性不同,总的来说,随着潜在蒸发量增大,气象因子的弹性系数逐渐降低,而下垫面因子的弹性系数明显增大。
(4)径流突变初期(1992—1999年),降水的显著减少是导致径流减少的主要原因,即气候因子对径流减少的贡献约占60%,人类活动的贡献约占40%;随着1999年泾河流域大范围退耕还林工程的实施以及人类引用水量的增加,人类活动对径流的减小起主导作用,气候变化贡献次之,其贡献分别为102%和-2%;纵观径流变化期,气候变化和人类活动对径流减少的贡献分别为80%和20%左右。
参考文献:
[1] 王浩,杨贵羽,杨朝晖.水土资源约束下保障粮食安全的战略思考[J].中国科学院院刊,2013,28(3):329-336,321.
[2] 周帅,王义民,郭爱军,等.黄河流域未来水资源时空变化[J].水力发电学报,2018,37(3):28-39.
[3] YE X, ZHANG Q, LIU J, et al. Distinguishing the Relative Impacts of Climate Change and Human Activities on Variation of Stream Flow in the Poyang Lake Catchment,China[J]. Journal of Hydrology, 2013, 494: 83-95.
[4] 张丽梅,赵广举,穆兴民,等.基于Budyko假设的渭河径流变化归因识别[J].生态学报,2018,38(21):7607-7617.
[5] 王国庆,张建云,管晓祥,等.中国主要江河径流变化成因定量分析[J].水科学进展,2020,31(3):313-323.
[6] 刘绿柳,王秀杰,张鹏飞.基于SWAT模型的气候变化和人类活动对伊洛河径流影响分析[J].人民珠江,2020,41(1):1-6.
[7] 周帅,王义民,郭爱军,等.气候变化和人类活动对黄河源区径流影响的评估[J].西安理工大学学报,2018,34(2):205-210.
[8] 杨大文,张树磊,徐翔宇.基于水热耦合平衡方程的黄河流域径流变化归因分析[J].中国科学:技术科学,2015,45(10):1024-1034.
[9] 黄斌斌,郝成元,李若男,等.气候变化及人类活动对地表径流改变的贡献率及其量化方法研究进展[J].自然资源学报,2018,33(5):899-910.
[10] 常斐杨,刘文兆,周海香,等.Budyko-Fu模型下气候季节性指标中水热变化时相差的选取研究[J].干旱地区农业研究,2019,37(3):208-214.
[11] 石清,邢万秋.基于变化的水热耦合平衡方程参数预测区域水资源量[J].华北水利水电大学学报(自然科学版),2020,41(1):35-43.
[12] 吴小宏,刘招,李强,等.泾河长系列水沙变化规律与归因研究[J].水资源与水工程学报,2019,30(6):144-149.
[13] PRIESTLEY C H B, TAYLOR R J. On the Assessment of Surface Heat Flux and Evaporation Using Large Scale Parameters [J]. Monthly Weather Review, 1972, 100(2):81-92.
[14] 李菲菲,饒良懿,吕琨珑,等.Priestley-Taylor模型参数修正及在蒸散发估算中的应用[J].浙江农林大学学报,2013,30(5):748-754.
[15] SAMANI Z. Estimating Solar Radiation and Evapotranspiration Using Minimum Climatological Data[J]. American Society of Civil Engineers, 2000, 126(4):265-267.
[16] 周园园,师长兴,范小黎,等.国内水文序列变异点分析方法及在各流域应用研究进展[J].地理科学进展,2011,30(11):1361-1369.
[17] LIU W L, LIU L N. Analysis of Dry/Wet Variations in the Poyang Lake Basin Using Standardized Precipitation Evapotranspiration Index Based on Two Potential Evapotranspiration Algorithms[J].Water,2019,11(7):1-22.
[18] 张晓琳,熊立华,林琳,等.五种潜在蒸散发公式在汉江流域的应用[J].干旱区地理,2012,35(2):229-237.
[19] 周帅,王义民,畅建霞,等.黄河流域干旱时空演变的空间格局研究[J].水利学报,2019,50(10):1231-1241.
[20] 赵勇,何国华,李海红,等.基于Choudhury-Yang公式的泾河流域蒸散发归因分析[J].南水北调与水利科技,2019,17(1):8-14.
[21] 郭爱军,畅建霞,王义民,等.近50年泾河流域降雨-径流关系变化及驱动因素定量分析[J].农业工程学报,2015,31(14):165-171.
【责任编辑 张 帅】
