波形腹板钢箱-混凝土组合梁桥的自振特性分析∗

冀 伟， 罗 奎， 闫林君

（兰州交通大学土木工程学院 兰州，730070）

1 问题的引出

波形腹板钢箱-混凝土组合梁桥是由混凝土顶板、波形钢腹板以及钢底板组成的新型组合结构，是对传统的波形钢腹板组合梁进行的改进。图1 为波形腹板钢箱-混凝土组合梁桥截面图。该桥型具有以下4 个优点：①外形美观、造型新颖、梁体制作方便、便于汽车运输和安装；②桥梁结构自重轻，跨越能力大，有效解决了传统混凝土腹板和底板易开裂的问题［1］；③降低截面的附加应力，提高了预应力导入度，使桥面板拉应力满足预应力A 类构件的要求，达到材料的优质组合；④利用压型钢板和预制板实现无模板施工，具有良好的发展前景。

图1 波形腹板钢箱-混凝土组合梁桥截面图Fig.1 Section diagram of steel box-concrete compositegirder with corrugated steel web

目前，众多学者已对波形钢腹板组合梁桥的屈曲性能、扭转性能、疲劳性能、抗弯性能以及长期效应等开展了大量的研究工作。John 等［2］推导了梯形波形钢腹板梁抗剪承载的计算公式，给出了波形钢腹板局部剪切屈曲系数。Shen 等［3］采用试验并结合有限元仿真模拟对单箱多室波形钢腹板组合箱梁桥的扭转性能进行了研究。Yuan 等［4］通过试验手段对波形钢腹板组合梁疲劳性能进行了研究，试验结果表明，最终的破坏模式为混凝土底板的剪切破坏以及波形钢腹板和混凝土底板连接处的层间滑移破坏。Köesdi 等［5］研究了弯曲变形和剪切变形的相互作用对波形钢腹板组合梁的力学性能的影响。Chen 等［6］研究了预应力对波形钢腹板组合梁桥力学性能的影响。罗奎等［7-9］考虑剪力滞和剪切变形效应的影响，对简支和连续波形钢腹板组合箱梁自振频率和挠度进行了研究。刘保东等［10］对波形钢腹板连续箱梁的弯剪受力性能和破坏机理进行了试验研究。李立峰等［11］推导了变截面波形钢腹板组合箱梁在偏心荷载作用下的畸变正应力的理论计算公式。周聪等［12］采用理论分析结合试验，对波形钢腹板组合箱梁桥的扭转性能进行了全过程分析。桂水荣等［13］研究了箱梁截面形式、横隔板的布置方式以及支座的横向约束方式对大跨波形钢腹板组合梁桥自振特性的影响。郑尚敏等［14］对单箱多室波形钢腹板组合箱梁的扭转性能进行了研究。冀伟等［15］在综合考虑波形钢腹板的剪切变形和箱梁的剪力滞的基础上，运用能量变分原理和Hamilton 原理，推导出波形钢腹板简支箱梁桥的自振频率计算公式，结合三弯矩方程推导出波形钢腹板连续箱梁桥的自振频率计算公式［16-17］。文献［15-17］的解析式只适用于特定的荷载和边界条件，需要建立ANSYS 空间有限元实体模型进行比较。因此，寻求一种波形钢腹板组合箱梁自振频率计算的简化分析方法具有重要的研究意义。

笔者在文献［15-17］的基础上，运用势能驻值原理，推导出波形腹板钢箱-混凝土组合梁桥的单元刚度矩阵和单元质量矩阵。采用Matlab 有限元软件编写了计算波形腹板钢箱-混凝土组合梁桥自振频率和振型的求解程序，为实际工程中波形腹板钢箱-混凝土组合梁桥自振特性的计算提供了一种简化的计算方法。

2 单元刚度矩阵和单元质量矩阵建立

2.1 基本假定

建立单元刚度矩阵和单元质量矩阵的基本假定如下：

1）只考虑波形钢腹板的剪切应变能，将其弯曲应变能忽略不计；

2）忽略混凝土顶板和钢底板平面外的切应变γxz和γyz以及正应变εy，仅考虑混凝土顶板和钢底板平面内的切应变γxy和εx；

3）不考虑波形腹板钢箱-混凝土组合梁的混凝土顶板和波形钢腹板交界处的滑移效应；

4）将钢筋的影响忽略不计。

波形腹板钢箱-混凝土组合梁的横截面构造形式如图2 所示。分析其自由振动时，根据文献［18］，该桥型的位移模式可用梁的竖向挠曲位移w和桥梁的纵向位移u进行描述，如式（1）和式（2）所示。

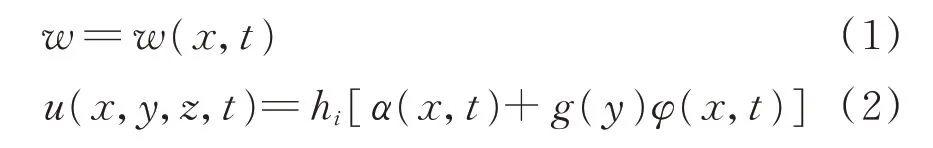
其中：b和ξb分别为波形腹板钢箱-混凝土组合梁混凝土顶板箱中部分长度的一半和悬臂板的长度；hi为箱梁整体截面的形心到顶底板形心的距离；α(x，t)和φ(x，t)为波形腹板钢箱-混凝土组合梁在发生自由振动时，弯曲变形引起的转角函数和剪切转角的最大差值函数。

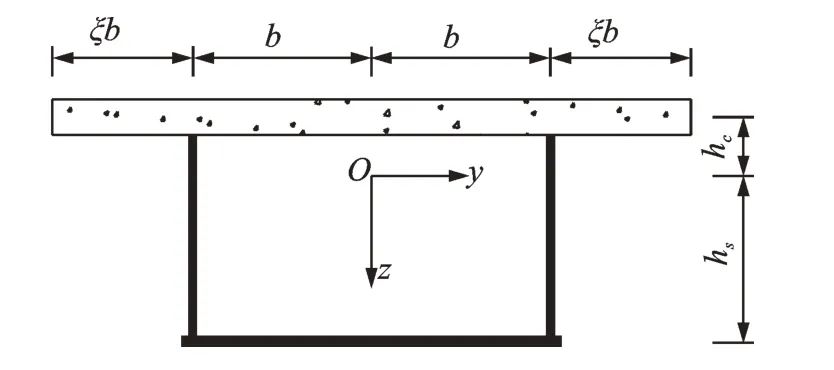
图2 横截面构造形式Fig.2 Structural form of the cross section of the boxgirder

根据文献［18］，g(y)的计算式为

2.2 总势能的建立

根据基本假设，得到波形腹板钢箱-混凝土组合梁各部分的应变能如式（4）～（7）所示。

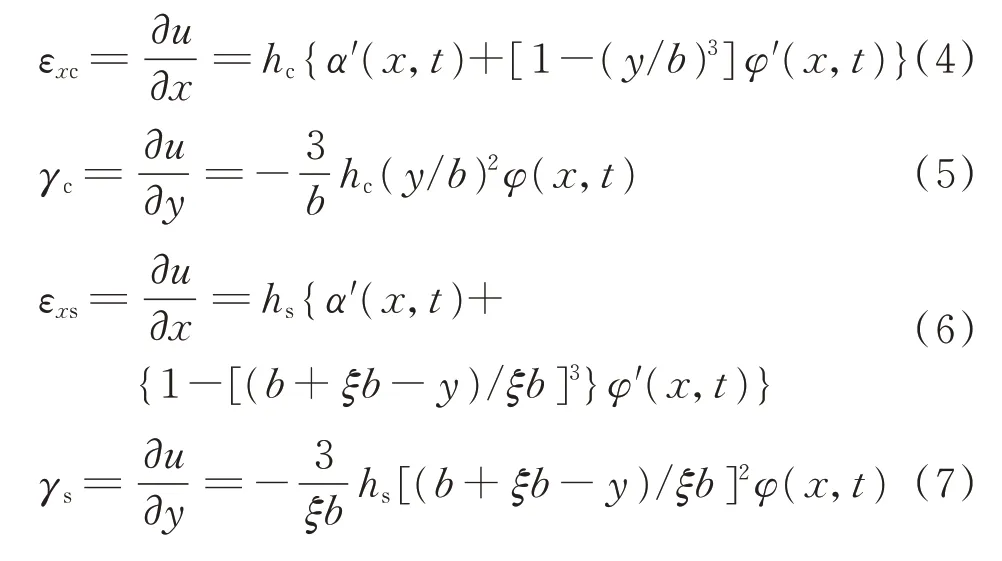
其中：α'(x，t)和φ'(x，t)分别为α(x，t)和φ(x，t)关于x的一阶导数。

波形钢腹板产生的剪切变形为

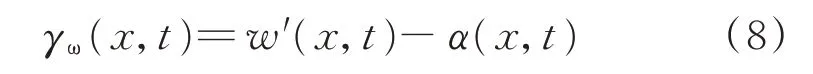
其中：w(x，t)为波形腹板钢箱-混凝土组合梁发生自由振动时，横截面的角位移函数；γω(x，t)为波形钢腹板的剪切变形。

波形腹板钢箱-混凝土组合梁的混凝土顶板、波形钢腹板以及钢底板的应变能分别为

波形腹板钢箱-混凝土组合梁的外力势能为

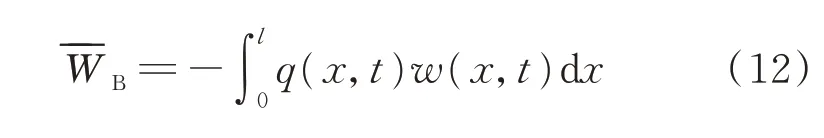
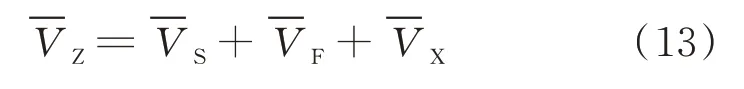
波形腹板钢箱-混凝土组合梁的总势能Π为

结合式（12）～（14），得到波形腹板钢箱-混凝土组合梁的总势能为

其 中：κ0=EcIc+EsIs；χ0=GcIc+GsIs；χ1=GωAω；Ic，Is分别为箱梁的混凝土顶板和钢底板对箱梁整体截面形心轴的惯性矩；Aω为钢腹板的横截面面积。

2.3 单元刚度矩阵的建立

波形腹板钢箱-混凝土组合梁的梁单元结点位移模式如图3所示。

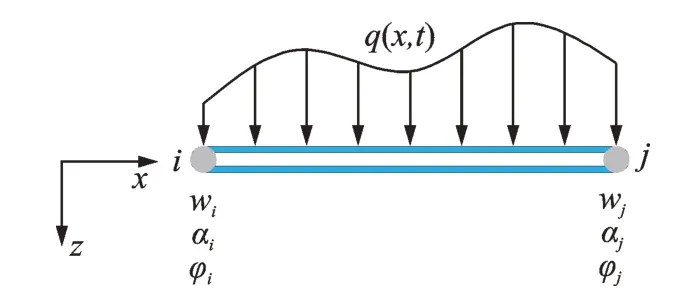
图3 有限元节点位移模式Fig.3 Node displacement mode of finite element

经计算得到满足工程精度的形函数N（x），根据形函数进行插值，有限元分析的结点位移模式如式（16）～（18）所示。

梁单元的平衡方程为

其中：

[F100]T；Ke，δe和Fe分别为波形腹板钢箱-混凝土组合梁的单元刚度矩阵、单元位移矢量以及单元荷载列阵。

形函数取为线性函数，即

将梁单元的结点位移代入总势能，得到波形腹板钢箱-混凝土组合梁的总势能

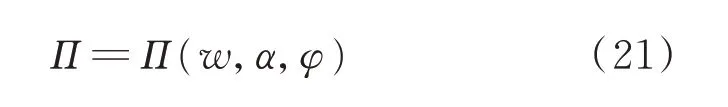
波形腹板钢箱-混凝土组合梁的总势能Π 取驻值的充分必要条件为

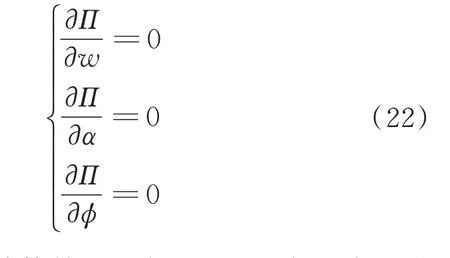
对式（22）的计算结果进行整理，写成矩阵的形式为

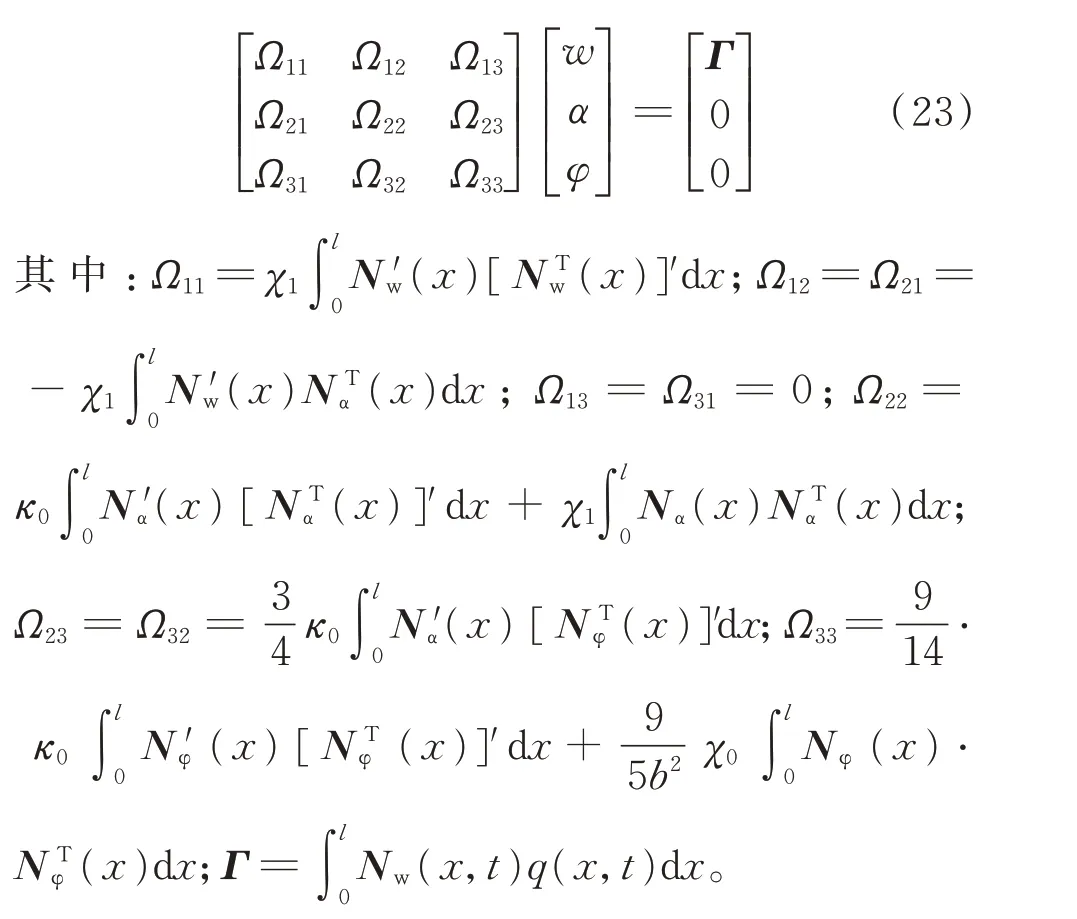
根据式（23），得到波形腹板钢箱-混凝土组合梁的单元刚度矩阵Ke为

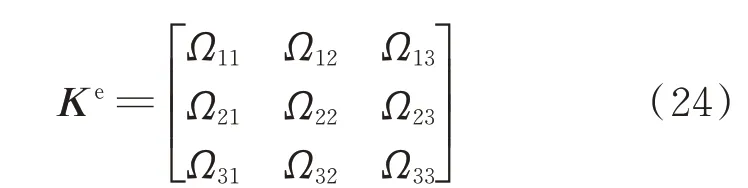
将波形腹板钢箱-混凝土组合梁桥单元刚度矩阵Ke分解为2 部分：弯曲项和波形钢腹板的剪切变形与箱梁剪力滞效应引起的耦合项

2.4 单元质量矩阵的建立

根据文献［19］，采用有限元分析波形腹板钢箱-混凝土组合梁时，单元质量矩阵为

其中：M为梁单元的单元质量矩阵；ρ为梁单元的质量密度；A为梁单元的截面面积；l为梁单元的长度。

根据笔者所推导的单元刚度矩阵和单元质量矩阵，采用Matlab 软件编制了计算波形腹板钢箱-混凝土组合梁振动特性的SFBOX 程序。限于篇幅，编程步骤不具体进行列举。

3 模型试验和有限元模型对比分析

3.1 波形腹板钢箱-混凝土组合梁的动力试验

选取我国正在建设的第1 座波形腹板钢箱-混凝土组合梁桥（即景中高速机场连接线主匝道高架桥）进行振动模态的实测，该桥的简支梁计算跨径为29.22 m，桥梁布置形式为单箱四室截面，景中高速机场连接线主匝道高架桥的单箱截面构造如图4所示。

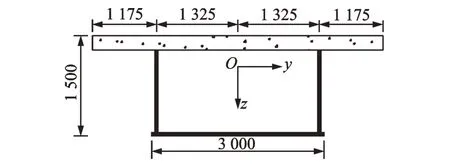
图4 单箱截面构造图（单位:mm）Fig.4 Cross-section structure diagram of a single box（unit：mm）

景中高速机场连接线主匝道高架桥的材料属性如表1 所示。波形腹板钢箱-混凝土组合梁的混凝土顶板的厚度为250 mm，波形钢腹板采用1200 型，波形钢腹板和钢底板的厚度分别为10 mm 和16 mm。箱中共设置6 道横隔板，钢底板上设置两道高度为180 mm 的纵向加劲肋。

表1 高架桥材料属性Tab.1 Material properties of viaduct birdge

采用东方所的INV3060S 型24位动态信号采集仪对波形腹板钢箱-混凝土组合梁的振动频率和振型进行实测，数据采集如图5 所示。箱梁顶板上采集器的平面布置图如6 所示。采样频率为256 Hz，通过试验测得桥梁结构的功率谱图如图7 所示，随后根据实测信号识别出各阶振动频率和振型。

3.2 ANSYS 模型的建立

采用ANSYS 18.0 三维有限元软件建立了景中高速机场连接线主匝道高架桥的空间有限元模型。由于波形钢腹板、钢横隔板和钢底板的厚度很薄，采用壳单元Shell 63 进行建模，混凝土顶板采用实体单元Solid 45 进行建模。钢底板和波形钢腹板的连接处采用共节点的形式，混凝土顶板和波形钢腹板的连接处采用刚性连接。ANSYS 三维有限元模型的边界条件按简支梁设置，建立的景中高速机场连接线的主匝道高架桥空间有限元模型如图8 所示。

图5 数据的采集Fig.5 Data collection

图6 箱梁顶板上采集器的平面布置图（单位:cm）Fig.6 Plan view of the collector on the top of the box girder（unit：cm）

图7 实测频率功率谱Fig.7 Measured frequency power spectrum

3.3 有限元模型分析结果和实测结果对比

利用笔者编写的SFBOX 程序计算波形腹板钢箱-混凝土组合梁的振动频率和模态时，将简支梁沿跨径方向划分为50 个等长的梁单元，共51 个结点。1 号 结 点 为 固 定 铰 支 座，将 其位 移Ux，Uy和Uz全 部进行约束，51 号结点为活动铰支座，将位移Uy，Uz进行约束。表2 为将SFBOX 程序计算的振动频率与景中高速机场连接线主匝道高架桥的实测结果以及ANSYS 空间有限元结果进行比较。其中：η为ANSYS 有限元值与SFBOX 计算值之差与SFBOX 计算值的比值；ξ为实测值与SFBOX 计算值之差与SFBOX 计算值的比值。

图8 主匝道高架桥空间有限元模型Fig.83D finite element model of main ramp viaduct birdge

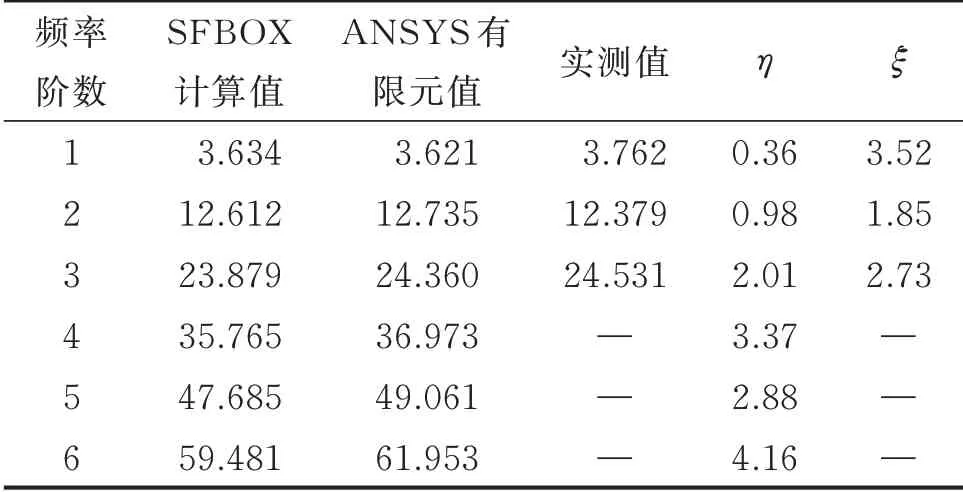
表2 不同方法下的振动频率比较Tab. 2 Comparison of vibrating frequencies of different methods Hz

从表1 可以看出：采用笔者编写的SFBOX 程序计算得到的波形腹板钢箱-混凝土组合梁桥的振动频率与ANSYS 空间有限元结果和实测结果的误差在5%以内，满足工程精度要求。这说明所提出的方法计算正确，结果可靠，具有较高的计算精度，使分析不同边界和荷载条件下的该桥型剪切剪滞问题变得简单易行，只需将复杂桥梁结构进行单元划分，输入截面参数，运行SFBOX 程序，即可得到结构的振动频率和振型，计算过程大大简化，避免了建立ANSYS 空间有限元模型的复杂性。可见，该方法具有广泛的工程实用性。

4 收敛速度分析

为了进一步研究笔者提出方法的收敛速度，将该波形腹板钢箱-混凝土组合梁桥分别划分为10，20，30，40 和50 个等长度的梁单元，采用笔者编写的SFBOX 程序对波形腹板钢箱-混凝土组合梁桥的振动频率进行了分析，不同单元数下的前6 阶振动频率如3 所示。

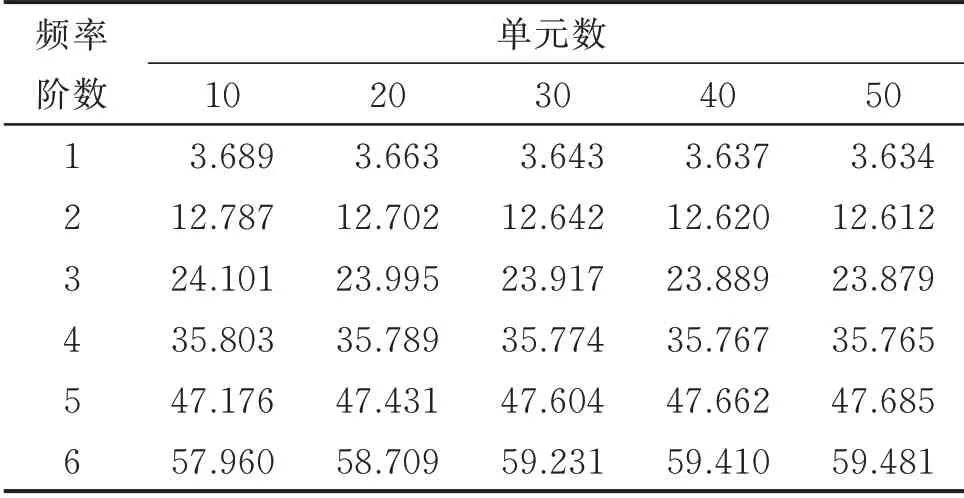
表3 不同单元数下的前6 阶振动频率Tab.3 Comparisons of vibrating frequencies of different number of element Hz

从表3 可以看出，笔者提出方法的收敛速度很快，说明编写的SFBOX 程序具有较高的计算精度，只需要较少的单元数，即可得到满意结果。

如表4 所示，为了进一步研究提出方法的计算效率，将所编写的SFBOX 程序与ANSYS 空间有限元模型求解景中高速机场连接线主匝道高架桥的振动频率所需的求解时间进行比较。其中，ς为SFBOX 程序结果与ANSYS 有限元结果的比值。

表4 不同方法计算振动频率所需时间的比较Tab. 4 Comparisons of the time required for calculating the vibrating frequencies by different methods

从表4 可以看出，笔者所提方法的计算速度很快，采用笔者所编写的SFBOX 程序求解景中高速机场连接线主匝道高架桥的振动频率所需的计算时间仅为用ANSYS 空间有限元模型求解用时的1.04%，大大缩短了计算时间，提高了计算效率。

5 结 论

1）采用笔者编写的SFBOX 程序计算得到的波形腹板钢箱-混凝土组合梁桥的振动频率与ANSYS空间有限元结果和实测结果的误差在5%以内，验证了笔者所编写的波形腹板钢箱-混凝土组合梁振动频率求解程序的可靠性。

2）通过对波形腹板钢箱-混凝土组合梁桥振动频率的分析，验证了SFBOX 程序具有较高的计算精度。在分析波形腹板钢箱-混凝土组合梁桥的动力特性时，只需要较少的单元数量，即可达到较高的计算精度。

3）SFBOX 程序的计算速度很快，故采用SFBOX 程序求解波形腹板钢箱-混凝土组合梁桥的振动频率，计算简便，大大缩短了振动特性求解的计算时间，提高了计算效率。

4）研究成果适用于不同边界条件和荷载条件下箱梁的剪切剪滞问题，只需将复杂结构进行单元划分，输入截面参数，运行SFBOX 程序，即可得到结构的动力特性，使得计算大大简化，避免了ANSYS 有限元模型建立和求解的复杂性，该方法具有广泛的工程实用性。