立式一体化泵闸安全性研究及结构优化∗

侍贤瑞， 严根华， 董 家， 杨 宇

（1.南京水利科学研究院 南京，210029）（2.河海大学水利水电学院 南京，210098）（3.水文水资源与水利工程国家重点实验室 南京，210029）

1 问题的引出

我国河道水系泵闸工程一般均采用分离式布置，该布置方式存在占地面积大、建设成本高和泵闸管理分散等缺点。随着城市化水平的提高，征地成本及环境要求使得这一缺点日益凸显。一体化泵闸具有工期短、占地小、运行费用低的优点，较好地解决这一难题，尤其适合于中小河流的水环境和水生态整治工程，具有广泛的应用前景及良好的经济和社会效益。

一体化泵闸将轴流式潜水泵安装在平板闸门上，泄水道与抽水道合二为一，既可按常规平板闸门排涝、挡水使用，又可在城区洪水来流量较大、无法自流泄洪时，启动水泵抽水强排。城市水景观工程中，当外河水位＜内河水位＜城市设计景观水位时，关闭闸门，启动水泵抽水以保证城市景观水位。

一体化泵闸如图1 所示。根据水泵的安装方式，分为立式和卧式2 种。立式一体化泵闸将水泵置于一个S 型流道的井筒之中，并将该井筒附加在平板闸门梁格上，检修方便，对下游水深要求较低，但流道复杂。卧式一体化泵闸将水泵置于圆筒中，该圆筒平卧贯穿安装在平板闸门面板上。

图1 一体化泵闸Fig.1 Pump gate

目前，国内外学者对轴流泵及平板闸门各自的流激振动特性研究较多。张德胜等［1］对变转速下轴流泵的压力脉动以及振动特性进行研究，发现模型不同位置的振动以1 倍频和2 倍频为主，垂向振动大于水平向。李忠等［2］研究了变工况下的轴流泵振动特性，发现振动量和流量的变化趋势和扬程与流量的变化关系基本一致。马斌等［3］对水工闸门振动现状进行了综述。沈春颖等［4］对平面闸门进行流场-振动同步测量，发现同工况下，当闸后漩涡顺水流方向靠近闸门，顺河向振动将达到峰值且为工况均值的4～5 倍。Chen 等［5］对用于改善河流水质的生态闸门泵进行了研究和优化。

由于水泵振动-井筒内水流压力脉动-河道内水流紊动的荷载组合极为复杂，其对泵闸结构的振动危害程度仍未知，因此该研究对一体化泵闸的应用有重要意义。笔者依托赛莱默（中国）有限公司的飞力一体化泵闸项目，对一门双泵的立式表孔一体化泵闸进行了研究，该装置宽为7.65 m，高为5.7 m（不含井筒）。建立有限元数值模型分析了结构静动力特性，并建立了比尺为1∶10 的水力学模型及水弹性模型，三者互相结合以研究泵闸在不同条件运行时的安全性。

2 静动力安全性数值分析

结构的静力特性分析包括应力和变形计算［6］。强度计算根据第4 强度理论进行校核。结构动力特性计算主要求解结构的固有频率和振型［7］，且泵闸与水流的耦合作用仅发生在固液交界处，故属第2 类流固耦合问题。结构离散化后的动力平衡方程为

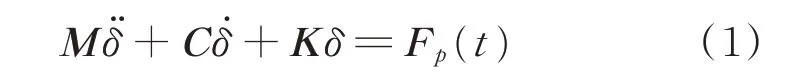
其中：M，C，K分别为结构的质量、阻尼和刚度矩阵；δ̈，δ̇，δ分别为结点的加速度、速度和位移；Fp(t)为结构耦合面上结点处的动水压力。

引入Φ（x，y，z，t）为水流扰动速度势，并与扰动压强p建立联系，根据流体的连续性方程可得

其中：S，D，T为引阵之间的转换矩阵。将式（2）代入式（1），得到

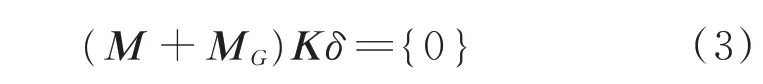
其中：MG为附加质量阵。

式（4）为在水介质下的结构自由振动的耦合控制方程，可表示为

因Mp为非对称矩阵，故可采用Lanczos 法进行求解。推导后得到

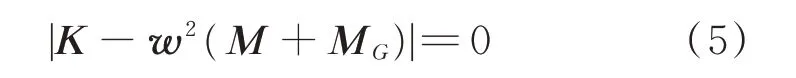
求解可得结构的n阶自振频率ω1，ω2，…，ωn。将其代入式（5），得到相对应的n个振型。

立式一体化泵闸有限元模型由422 个体单元构成；单元划分尺寸为0.04 m；离散单元采用solid187单元，共离散710291 个单元，212179 个节点。边界条件为：底缘及肘型流道垫脚y向位移为0，背向滑块z向位移为0，导向轮x向位移为0。

2.1 静力计算

静力计算中，在闸门面板施加5.1 m 静水压力。计算结果表明：泵闸最大位移为0.46 mm，发生在肘型流道进口处；主横梁最大挠度为1/18500；结构最大应力为104 MPa，发生在泵闸上部导向轮筋板处，其余部分均低于50 MPa。数值计算结果如图2 所示，结构满足刚度和强度要求。

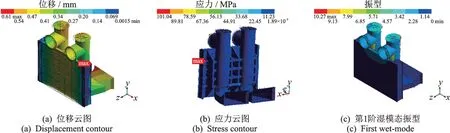
图2 数值计算结果Fig.2 Results of numerical simulation

2.2 动力计算

数值计算结果表明：湿模态第1 阶振动频率为12.41 Hz，其振型为两水泵沿顺河向摆动。第2 阶振动频率为12.60 Hz，为两水泵沿横河向摆动。由计算结果可知，水泵与井筒的联结性较弱，导致结构基频较低。立式一体化泵闸的优势之一为水泵易于检修，只需将井筒顶部的封盖打开，就可将水泵调出检修，故不可在井筒上部增加侧向支撑。因此，需要进行模型试验来评价结构的安全性。

3 模型试验

建立了几何比尺Lr=10（即模型比例为1∶10）的水力学及水弹性模型各一套，分别研究泄水工况下结构所受水动力荷载、泄水抽水工况下结构的振动特性。采用江苏东华测试DH5922N 动态采集仪，试验水槽如图3所示，其中：D为门槽宽度，D=107 mm。

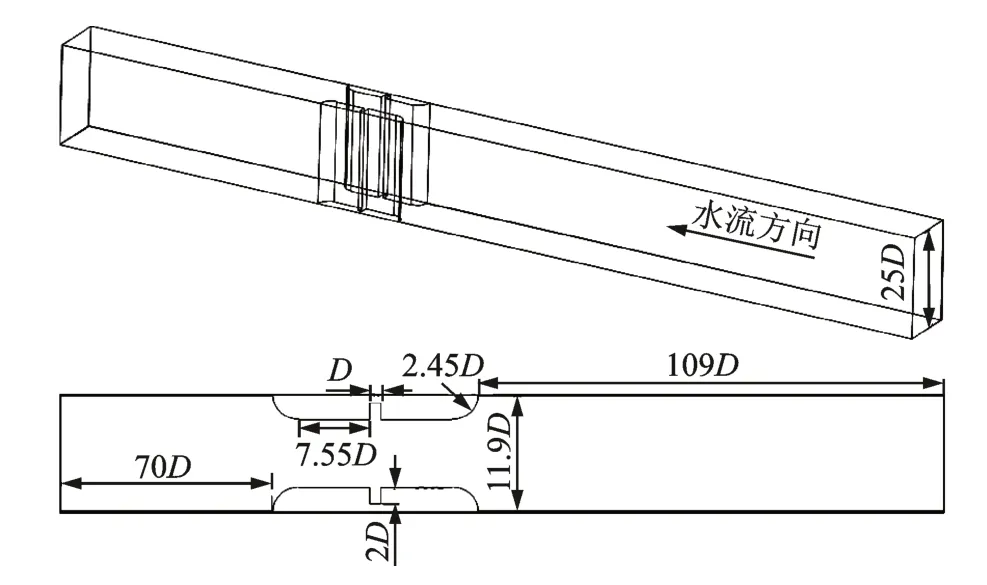
图3 试验水槽（单位：mm）Fig.3 Experiment water channel (unit:mm)

3.1 试验模型及传感器布置

1）水力学模型。为掌握泄水工况下泵闸结构面板及肘型流道附近的动水压力分布，在闸门面板及肘型流道共设置25 个时均压力测点（M1～M25）和8 个脉动压力传感器（P1～P8）。

2）水弹性模型。根据动力试验相似准则可得，材料密度比尺ρr= 1，弹模比尺Er=Lr= 10，泊松比比尺μr= 1，水弹性模型的材料密度为7850 kg/m3，弹性模量为2.1×104MPa，泊松比为0.3。模型水泵比转速与原型泵相同［8］。原型泵直径为1400 mm，额定转速为495 r/min，额定扬程为7.7 m，额定流量为4.3 m3/s，名义比转数为810，效率为84.5 %。为了获取泵闸在运行过程中的振动特性，在泵闸构重点部位布置了4 个三向振动加速度传感器（A1～A4），分别测量顺河向（x），横河向（y）及垂向（z）的振动加速度。动水压力及振动加速度测点布置如图4 所示。

图4 动水压力及振动加速度测点布置Fig.4 Dynamic pressure measuring points & acceleration measuring points

3.2 基于HHT 的时频分析介绍

信号处理采用随机振动理论及Hilbert-Huang变换分析［9］。首先，将原始信号经经验模态分解（empirical mode decomposition，简称EMD）成一系列固有模式函数（intrinsic mode function，简称IMF）和残差的组合；其次，对每个IMF 利用解析信号相位求导，计算出有意义的瞬时频率和瞬时幅值，获得信号的Hilbert 时频谱。该方法无需信号的先验知识，分解过程完全由数据自身驱动，克服了快速傅里叶变换（fast Fourier transform，简称FFT）无法获得信号的时频信息、短时傅里叶变换的时域、频域分辨率相矛盾以及小波变换对小波基的敏感和信号能量泄露等问题，具有自适应性、完备性、近似正交性和IMF 分量的调制性，是一种后验的方法。

3.3 水动力安全性评价

水动力试验的目的在于研究各工况下的水流流态、不同测点的时均及脉动压力变化规律和量值，为水弹性试验奠定基础。泄水试验工况组合如表1所示。

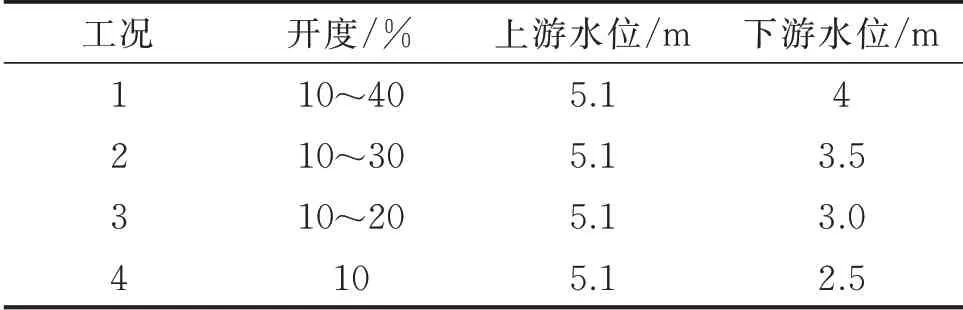
表1 泄水试验工况组合Tab.1 Water discharge test conditions

3.3.1 时均动水压力特征

试验结果表明，泵闸面板及底缘压力随上下游水位及泵闸开度的不同而呈一定变化规律，上游侧测点时均动水压力水头接近上游侧水位，下游侧测点时均动水压力随泵闸开度的不同而存在一定变幅，测点越接近门体，变幅越大，随后逐渐降低直至接近下游水深。水流过闸后，部分势能转换为动能，流速增高而压力降低。闸门底缘处流态复杂，部分工况存在负压，最大值为−0.71×9.8 kPa。

3.3.2 脉动水压力特征

水流脉动压力是泵闸泄水过程中引发流激振动的主要动荷载，包括由水跃、波浪对门体冲击引起的压力脉动，压力脉动强度及功率谱特征对泵闸振动量造成影响。试验结果指出，泵闸结构的总脉动压力荷载随闸门开度的增加呈先增后减的趋势。随着上下游水位差的逐渐增大，结构的总脉动压力峰值依次出现在开度为40%，30%，20%，10%（即工况1-4，2-3，3-2，4-1）；不同部位各测点的脉动压力均方根值都没有超过3.1 kPa，功率谱分析得出泵闸水流脉动压力功率谱密度的高能区主要集中在0～10 Hz 的低频区，主频在5 Hz 范围内，脉动水压力均方根值（root mean square，简称RMS）特征如图5 所示。

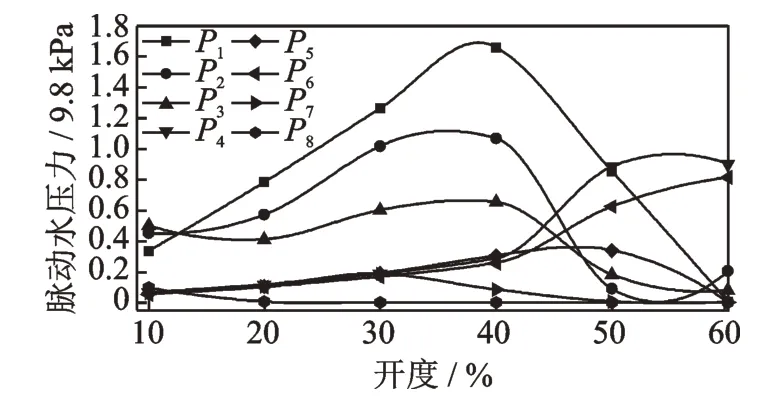
图5 脉动水压力均方根值特征Fig.5 RMS characteristics of Fluctuating Pressure

4 振动安全性评价

结构振动安全性评价通过水弹性模型试验进行，试验分泄水与抽水两大工况。泄水试验的工况选取脉动压力出现峰值的工况1-4，2-3，3-2 和4-1。抽水试验工况以电机频率正常工作状态（50 Hz）为主要研究工况，同时还考查了60 Hz 超频模式和30 Hz 低频节能模式下的泵闸运行状态。立式一体化泵闸的井筒出水口悬于闸门之上，抽水时出射的水流使上游形成回流冲击泵闸上部。为解决该问题，在井筒出水口处各安装一拍门，用来消减出射水流的能量。因此，设置无拍门的工况1-4 对拍门减振效果进行试验论证。抽水试验工况组合如表2所示。

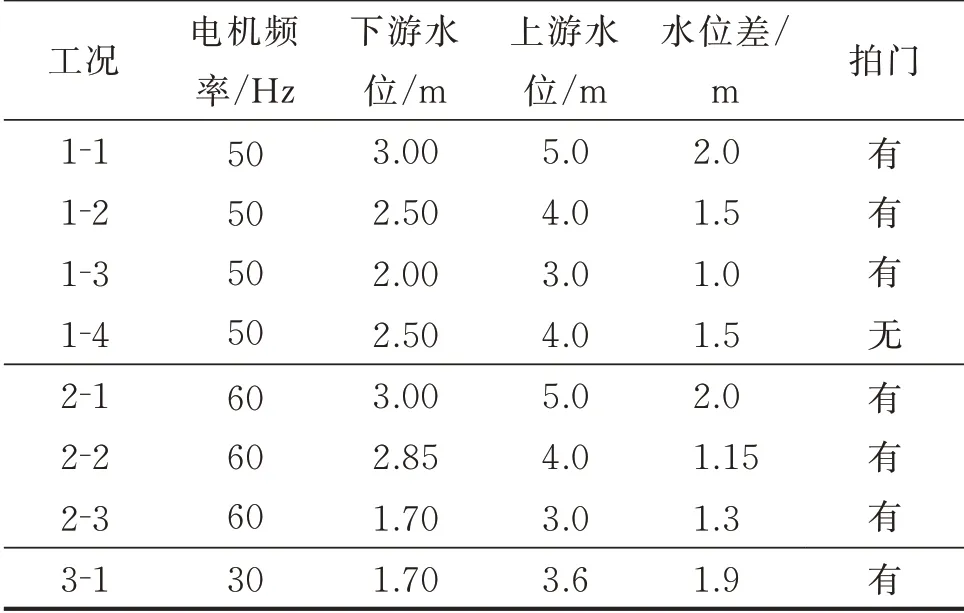
表2 抽水试验工况组合Tab.2 Pumping test conditions

4.1 泄水工况振动特性

试验结果表明，结构振动加速度整体上呈上部大、下部小的态势。振动加速度均方根值在工况3-2肘型流道收缩断面处垂向达到最大，为0.798 m/s2。由时频图可知，频率集中在10 Hz 以内，时间历程上也较为均匀。测点4 垂向加速度明显大于横河向及顺河向，表明下泄水流形成的水跃对肘型流道有着强烈的冲击作用。泄水工况振动加速度特征如图6所示。

图6 泄水工况加速度特征Fig.6 Acceleration characteristics of water discharge

4.2 抽水工况振动特性

抽水工况下泵闸结构荷载情况更为复杂，除了承受静水压力、水流荷载的冲击作用外，还承载水泵运转带来的振动载荷作用。试验结果表明：泵闸各测点振动加速度均方根值随转速加快而增加，随上游水位的降低而增加。水泵拍门的安装有助于减小结构振动量。拍门的增加有效减小了井筒顶部的振动量，顺河向、横河向及垂向的振动量分别减少51.4 %，45.5 %及38.2 %，可见，出射水流有相当一部分能量被消耗。门体侧边部位（A3测点）顺河向振动量略有增加是因为拍门使得出射水流沿横河向分散，导致泵闸侧壁区域回流强度增加。整体上看，泵闸结构振动量在工况3-1 肘型流道处垂向达到最大，为1.76 m/s2；在工况1-4 侧壁横河向达到最大，为0.99 m/s2；在工况2-2 侧壁顺河向达到最大，为1.73 m/s2。

水泵电机频率分别为50，60 及30 Hz 时，叶频分别为24，29 及14.5 Hz，频谱分析结果体现了这一特征（FFT 频率分辨率取值导致些许偏差）。频率集中在24 Hz 左右，时间历程上也较为均匀。抽水工况加速度特征如图7 所示。

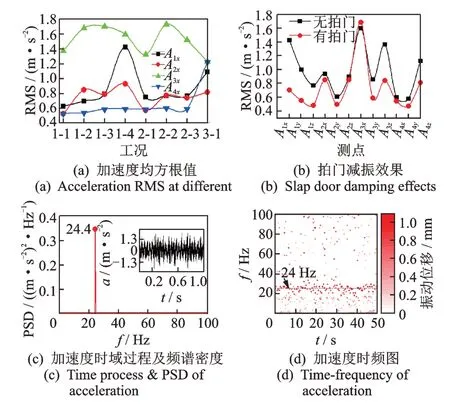
图7 抽水工况加速度特征Fig.7 Acceleration characteristics of pumping condition

5 结构的抗振优化

由上述研究可知，泵闸结构的侧壁振动量较大，需采取措施进行振动控制。从重量优化［10］、被动控制减振、局部加强、减小井筒内水流冲击性和加强整体刚度的角度出发，对结构进行了一系列抗振优化。图8 为泵闸结构抗振优化方案，包含：①在门体、水泵井筒中心轴线处配置10 t 配重；②在闸门上游增设反向支承和侧向支承橡胶阻尼减振垫；③在井筒上部结构增加支撑横梁，以抑制顶部水平向振动量；④在井筒出水口与闸门交界处增加筋板；⑤修圆立式泵闸井筒90°流道拐角，顺畅水流流线；⑥增加肘型流道斜拉杆刚度；⑦加强两个井筒出水口的联结性。因原方案的1-3 工况为泵闸电机常频运行条件下出现最大振动量（A3x，1.70 m/s2）的试验工况，故取其为对比工况。此外，为全面掌握优化方案结构的振动特性，优化试验增设一激光位移传感器测量A2测点的垂向振动位移。

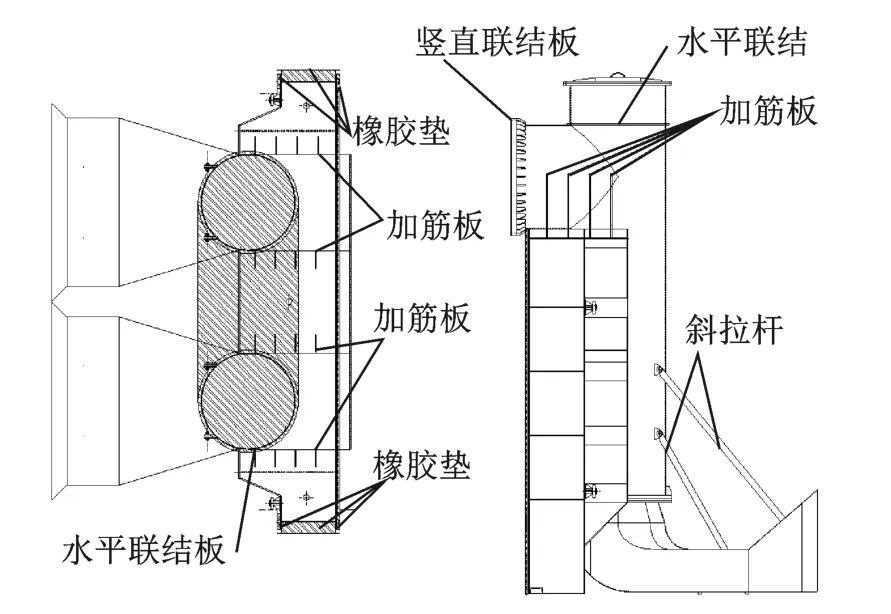
图8 泵闸结构抗振优化方案Fig.8 Vibration resistance optimazation scheme of pump gate

试验结果表明，泵闸结构修改方案的振动量出现明显下降，振动加速度最大均方根值出现在泵闸井筒顶部顺水流向，为1.03 m/s2，降低了39%。泵闸侧向振动量（A3y）降低了45%，频率集中在24 Hz左右，时间历程上也较为均匀。优化措施取得明显抗振效果，如图9 所示。

图9 优化效果Fig.9 Optimization effects

6 结 论

1）通过静力分析发现，导向轮的应力虽然处于安全范围内，但较结构其余部分大得多。这是由于泵闸挡水时面板整体呈拱形，导致导向轮结构挤压应力相对较大，建议将导向轮改成弹性支撑，延长使用寿命的同时，也起到一定的减振效果。

2）对于水泵抽水运行中结构振动加速度过大的问题，对结构体型进行了优化调整，将结构最大振动加速度均方根值由1.7 m/s2降至1.03 m/s2，抗振优化效果明显。鉴于抽水工况水流运动和荷载作用复杂，对泵闸结构焊接工艺提出更高要求，防止疲劳破坏并综合考虑启闭方式。

3）水泵超频运行，振动量较大，不可长时间运行。上下游水位差较大且下游水位较低时，水泵低频运行的工作效率低。井筒内水量不足会导致结构振动量激增，应避免使用。

4）泵闸一体化装置具有结构布置紧凑、占地面积小及工程投资节省等优点，建议在中小型泵闸工程上推广应用。