一种振测数据最佳分析长度的确定方法∗
2021-03-03张建伟马晓君程梦然
张建伟, 李 洋, 马晓君, 程梦然
(1.华北水利水电大学水利学院 郑州,450046) (2.水资源高效利用与保障工程河南省协同创新中心 郑州,450046)(3.河南省水工结构安全工程技术研究中心 郑州,450046)
引 言
根据结构动力响应变化进行结构损伤诊断或安全监测研究,是目前工程界研究的热点问题之一。通常,结构在损伤诊断和在线监测等过程中的振测数据长度大多为人为选取,而振测数据的分析[1-3]作为检测结构振动状态的关键依据,其长度的选取尤为重要,在一定程度上决定着结构监测的有效性。因此,需要一个有效的数据长度选取方法来确定数据的最佳分析长度。
陈佳袁等[4]对小样本水文数据序列进行优化处理,将对时间序列的分析用于水文数据的预测,可提高流量数据的预测精度。马佳妮等[5]利用长时间序列遥感数据,构建了一种反演净初级生产力(net primary productivity,简称NPP)的耕地质量评价方法,可同时获取耕地质量空间分布和时空演变过程,减少数据断点导致的评价误差,提高了准确性。蒋增林等[6]利用趋势移动平均方法和指数平滑方法,对电力系统负荷时间序列历史数据进行处理,取得较好的预测效果。时间序列数据的分析及应用在许多领域都有所涉及[7-9],但对数据长度的合理性分析较少。MPE 是Aziz 等[10]在排列熵(permutation entropy,简称PE)的基础上提出的一种检测动力学突变和时间序列排列的方法,具有灵敏度高、抗噪能力强和鲁棒性强等特点,可以较敏感的反应非线性、非平稳信号时间序列的微小变化[11]。由于该方法在检测系统动力学突变方面较为敏感,因此成为数据分析的热点方法,被广泛应用于生物医学[12-14]、机械损伤诊断[15-16]及股票分析[17]等领域,具有较好的工程实用性。MPE 计算振测信号数据时,数据量的大小决定了包含信号的丰富程度。数据长度过长,存在计算时间长等缺点;数据长度过短,会导致信号的特征信息不完全。因此,选取合适的数据长度是保证分析结果正确的重要环节,笔者利用MPE 算法求取振测数据的最佳分析长度,并将其应用于具体泄流工程。
1 基本原理
1.1 多尺度排列熵
MPE 算法相较于PE 算法具有更好的鲁棒性,能够很好地检测信号的复杂程度[18]。将一维时间序列进行粗粒化处理,选取合适的尺度对其进行多尺度化,分别计算各尺度下时间序列的PE 熵值,继而得到MPE。
首先,令{X(i);i=1,2,…,n}为一维时间序列,粗粒化处理可得
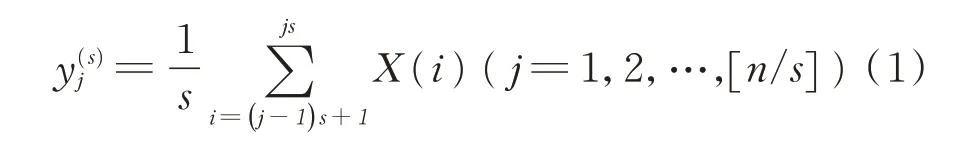
由式(1)可知,时间序列长度与尺度因子s的大小成反比。令m为嵌入维数,τ为延迟时间,对粗粒化序列重构得到重构粗粒化序列及重构分量
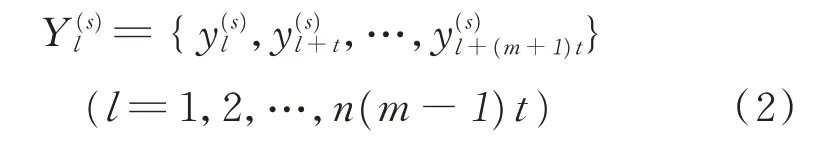

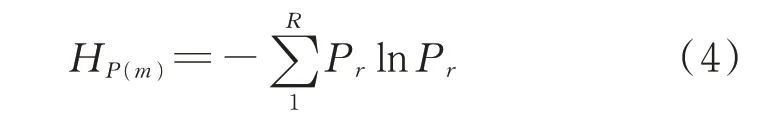
将PE 归一化处理,可得

HP的值表示粗粒化后时间序列的随机程度。时间序列的随机程度越低,HP的值越小;反之,该时间序列的随机程度越高,复杂度越大。
由此可知,根据粗粒化处理后的原始时间序列{X(i);i=1,2,…,n}可以得到s尺度下的粗粒化时间序列,分别计算其PE 熵值Hp,得到该原始时间序列的MPE,即Hmp(X)={Hp(1),Hp(2),…,Hp(s) }。
1.2 改进的粗粒化方法
粗粒化过程的优化如图1 所示。对时间序列进行粗粒化处理的MPE 计算,其目的是为了根据合适的尺度因子,将长度为N的原始时间序列分成s个不相重叠的窗口,分别计算每个窗口内数据点的均值,构成一组新的时间序列。将原始时间序列直接除以尺度因子时,若s值较大,则会导致新建窗口内时间序列长度过短;若序列中数据个数太少,会造成MPE 熵值计算结果不精确。

图1 粗粒化过程的优化Fig.1 Optimization of coarsening process
针对此问题,将移动平均粗粒化过程应用于MPE 计算中,如图1(b)所示[19]。已知尺度因子,通过移动平均粗粒化过程得到对应序列
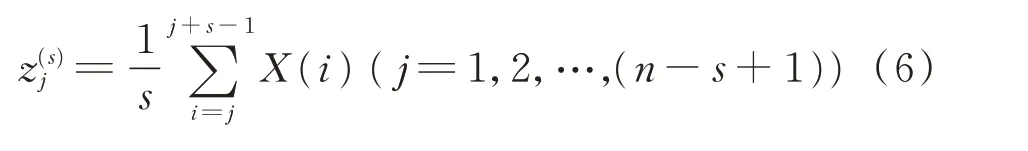
粗粒化处理后的序列长度为(n−s+1),若取原始时间序列长度为600,s=10,相较于原始粗粒化处理后得到的序列长度60,改进的粗粒化处理得到的序列长度却为591,数据长度会直接导致包含信息量的不统一。由此可知,改进后的粗粒化方法可以提高计算结果的准确性。
1.3 相空间重构参数的选取
计算各粗粒化序列的PE 熵值之前,需分别确定嵌入维数m与延迟时间τ。m与τ值的计算有独立确定与联合确定2 种方法,虽然2 种方法各有优缺点,但在检测结构的异常情况时,独立确定方法有更高的精确性[20]。因此,分别以伪近临法(false nearest neighbor,简称FNN)与互信息法(mutual information,简称MI)求取m与τ。参数选取的准则是:恰当的维数m为相空间中伪近临点的百分比趋于0 时对应的维数,且该维数之后,伪近临点的值不发生改变;最佳延迟时间τ为互信息第1 次达到最小值所对应的延迟时间,实测数据中m≥2,τ≥1。
1.4 最佳数据分析长度的选取
基于IMPE 的最佳振测数据分析长度的确定步骤如下:
1)通过设置传感器采集振测数据{X(i);i=1,2,…,n};
2)粗粒化处理信号数据,根据振动信号长度选择适合的尺度因子,利用移动平均粗粒化方法计算粗粒化序列
3)相空间重构,各粗粒化后数据的相空间重构参数m,τ根据FNN 与MI 选取;
4)计算粗粒化后各时间序列的PE 熵值PE1,PE2,…,PES,得到MPES= {PE1,PE2,…,PES},令以MPE 作 为 衡 量振测数据复杂程度的依据;
5)同一振动条件下,计算振测数据不同长度的MPE 均 值MPE(N1),MPE(N2),…,MPE(Ni),…,MPE(Nn),随着N不断增大,MPE 熵值逐渐稳定于一定值,当MPE(Nn)−MPE(Nn−1)≈0 时,不再增加数据长度,此时以MPE(Nn)作为标准熵值,MPE(Nn)所对应的数据长度Nn作为标准数据长度;
6)根据精度要求MPE(Ni)≥97%MPE(Nn),将MPE(Ni)与MPE(N1),MPE(N2),…,MPE(Ni),…,MPE(Nn) 进行比较,选出满足精度的MPE(Ni),将MPE(Ni)所对应的最短数据长度定义为振测数据最佳分析长度。
2 仿真试验
2.1 验证改进的粗粒化方法
改进粗粒化方法在MPE 上有较大优势,选取数据长度较短的白噪声,计算其在尺度因子s∈[1,15]时,优化前后粗粒化方法的熵值,以检验其优异性,白噪声熵值变化如图2 所示。
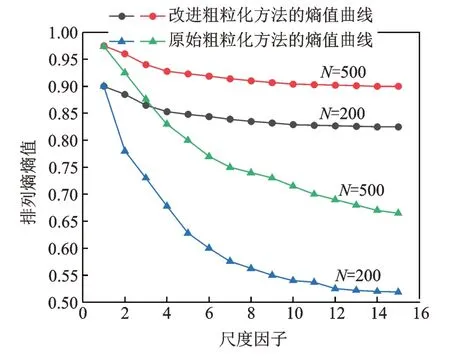
图2 白噪声熵值变化图Fig.2 Variation of white noise entropy
由于白噪声是所有频率具有相同能量的随机噪声,因此其时间序列的理论熵值为1。在实测过程中,熵值的精度会受到数据长度的影响,在选取白噪声数据长度N=200,500 时,其数据实测PE 熵值在0.90~0.97 范围内。由图2 可知,经原始与改进两种粗粒化方法处理后的白噪声熵值均随尺度因子的增大而逐渐减小,可验证式(1)和式(6)的正确性,数据长度的降低会增大理论值与真实值的差距。由于受尺度因子的影响较小,随着数据长度的增加,熵值减小的速度远低于原始粗粒化方法处理的白噪声的熵值,故提高了计算精度。可见,当数据长度与尺度因子相同时,改进粗粒化方法计算得到的实测熵值更接近于理论值。此外,根据计算结果可得,不论粗粒化方法改进与否,N=500 的白噪声信号的熵值均比N=200 的白噪声信号熵值更精准。这表明不仅粗粒化方法的选取会影响信号的熵值精度,数据信号的序列长度也是影响熵值准确度的重要因素。
2.2 检验数据长度对MPE 的影响
从仿真分析可知,序列长度会影响熵值的精准性。序列长度过大,存在计算繁琐、耗时长和突变处模糊化等弊端;序列长度过短,会导致包含特征信息的数据缺少或丢失,导致其熵值的可信度偏低。因此,需要寻找一个合适的序列长度以确保计算结果的精确性。笔者选取具有标准熵值的白噪声信号进行分析,不同数据长度下白噪声熵值变化曲线如图3 所示。可见,信号的数据长度越长,其熵值趋近于真实值1;尺度因子越大,对数据长度的影响越小,熵值越准确。这说明MPE 熵值对信号的数据长度以及尺度因子的变化较敏感,且当数据长度达到4000~5000 时,熵值的变化极为轻微,最后稳定于0.998,说明实测数据的熵值只会无限趋近于真实值,其精准度存在一定界限。因此,在信号分析中仅在一定长度范围内存在数据越长、分析越准确的现象,并不会无限精确。
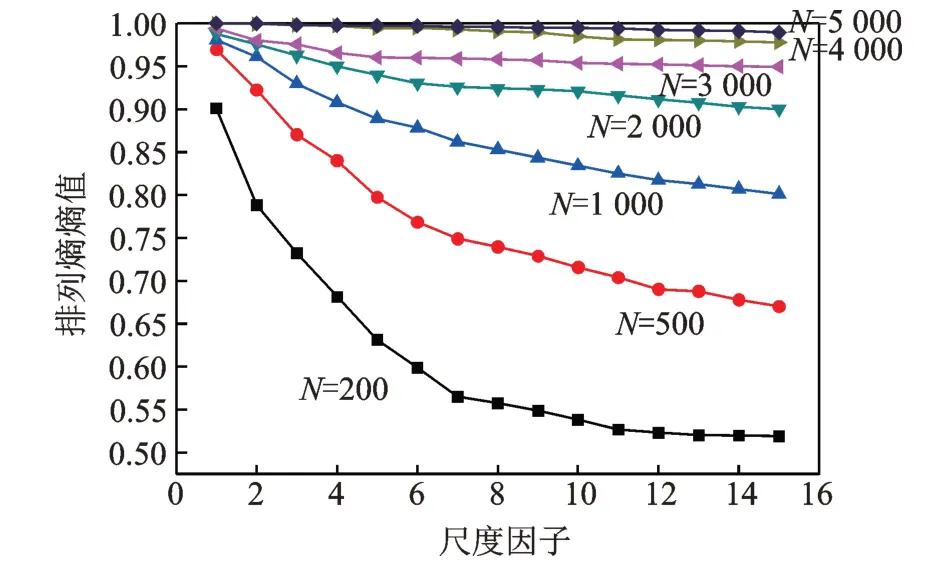
图3 不同数据长度下白噪声熵值曲线Fig.3 Variation of white noise entropy value at different sequence lengths
当MPE 熵值随数据长度的增加而趋于稳定后,选取此时的数据长度与MPE 熵值设定为标准序列长度与标准熵值。为提高计算效率,在保证分析结果准确的条件下,选取满足标准熵值97%精度的熵值作为有效熵值,所对应的振测数据长度作为最佳分析长度。当白噪声的数据长度N=5000 时,熵值趋于稳定值0.998,与理论值相差甚微。因此,选取数据长度N=5000 时所对应的熵值0.998 作为标准熵值,选择满足标准值97%精度的熵值即0.968 所对应的数据长度作为最佳分析长度,选取数据长度N=3000(对应熵值为0.971)作为该白噪声数据的最佳分析长度。
2.3 构造仿真信号
为验证选取数据最佳分析长度方法的可靠性,构造了仿真纯净信号f1(t)与白噪声f2(t),其表达式分别为

其中:t为时间;m为样本数;randn(m)为白噪声,其服从标准正态分布;采样频率f=100 Hz。
向纯净信号f1(t)中添加信噪比(signal noise ratio,简称SNR)分别为5%,10%,20%,30%,40%和50%的白噪声f2(t),根据上述方法,分别选取数据长度为N=500,800,1000,1500,2000,2500,3000,3500,4000,4500 和5000 的加噪信号,计算其熵值曲线。加噪信号熵值变化如图4 所示。
由图4 可知,加噪信号的熵值随数据长度的增长而增加,当数据长度达到4000~5000 时,熵值基本稳定在0.998,与白噪声信号有相同的变化规律。因此,选取满足标准熵值97%精度的熵值所对应的数据长度N=2000,作为加噪信号的振测数据最佳分析长度。在数据长度达到最佳数据长度后,不同信噪比的加噪信号的熵值趋于同一稳定熵值,可证明多尺度排列熵具有较强的抗噪能力和较好的鲁棒性,可有效判断信号的状态。
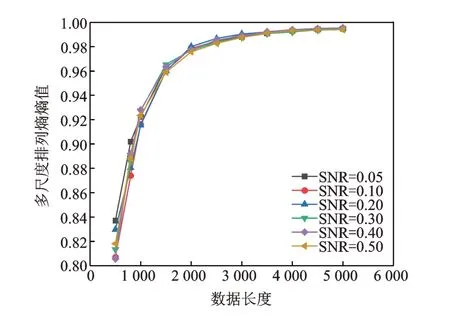
图4 加噪信号熵值变化曲线Fig.4 Signal entropy values with different white noise
3 工程实例分析
三峡大坝是三峡水利枢纽的主体建筑物,各种运行工况下大坝存在不同的激励源,使坝体振动较为复杂,对其监测及研究也较多[21-22]。以三峡大坝5号溢流坝段为研究对象,测试现场及传感器布置如图5 所示。信息采集由设置在结构表面的传感器完成[23],为保证收集效果,避免遗漏系统特征信息,坝体共放置了6 个传感器,如图5(b)所示。为全面反映坝体的振动特性,选取1#,2#,3#,4#测点水平向与垂向动位移传感器两类振动状态的1~6 通道的振测信号作为研究对象,采样时长为40 s,采样频率为100 Hz。
根据FNN 与MI 分别确定相空间重构参数m和τ。经计算,5 号溢流坝段坝体振动在1~6 通道的6种状态下的相空间重构参数分别稳定在m=4,τ=4 状态。相空间重构参数的选取如图6 所示。
图7 为三峡5 号溢流坝段6 个通道的振动信号熵值变化曲线,选取了N=200,500,1000,2000,3000 和4000 等6 种不同的序列长度。可见:各通道振动信号的熵值各不相同,水平向动位移振动熵值(1~4 通道)均比垂向动位移振动熵值(5,6 通道)所测的熵值小;熵值随数据长度的增加而逐步递增至平稳,当数据增加到一定长度时,熵值趋于一稳定值,与白噪声信号具有相同的规律。这说明利用MPE 方法选取信号分析长度是可行的,各通道在数据长度N=2000 时的熵值均达到稳定状态,对应的熵 值 分 别 为0.773,0.774,0.789,0.766,0.847 和0.928,依据97%的精度要求,计算各工况下最佳数据分析长度均为N=1000。

图5 三峡大坝5 号溢流坝段测试现场及传感器布置Fig.5 Field test and measuring point layout of No.5 overflow section of Three Gorges Dam

图6 相空间重构参数的选取Fig.6 The Selection of parameters for phase space restructure

图7 坝体不同工况下的熵值变化图Fig.7 Entropy change diagram of dam body under different conditions
4 结 论
1)该方法的提出为信号分析提供了可靠的数据长度,排除了人为选择数据长度导致的随机性与主观性,提高了振动监测的精确程度,便于对结构振动状态进行准确判断。
2)通过对信噪比不同的加噪信号计算分析,验证了多尺度排列熵具有较强的抗噪能力和较好的鲁棒性,可有效避免混杂噪声对计算结果精度的影响。
3)仿真实验数据与具体工程的分析结果表明,数据的长度与其熵值的精确性和稳定性密切相关,最佳数据分析长度所对应的熵值满足标准熵值97%,即可满足工程精度要求。
