主轴系统在线动平衡质量补偿策略优化

王 展， 张 博， 张 珂

（1.沈阳建筑大学机械工程学院 沈阳，110168）（2.高档石材数控加工设备与技术国家区域联合工程实验室 沈阳，110168）

引 言

质量不平衡是主轴常见故障之一，对于类似机床主轴系统的高精密旋转机械，微弱的质量不平衡会严重影响运转精度和质量［1］。在线动平衡技术是解决旋转机械不平衡振动问题的有效方案，可以通过移动动平衡装置质量块来补偿不平衡质量的方式，达到在线动平衡的目的［2］。

实施动平衡的核心在于能高效、高精度地完成质量补偿，如何能够更准确地计算动平衡补偿量、且更快速地完成质量补偿是提高动平衡精度和效率的关键点。因此，针对在线动平衡调控方法以及质量补偿策略方面的研究成为近年来国内外研究的热点。张珂等［3］测试了一种电磁滑环式在线动平衡装置的平衡特性，基于影响系数法进行了在线动平衡实验研究，为高速主轴双面动平衡和模态分析研究打下了基础。Diaz 等［4］利用模态分析对平衡配重及其角度位置进行先验评估，从而使模态平衡过程更加简单安全。Tsai［5］同时利用影响系数法和遗传算法，得到每个平衡面的平衡配重和相位，从而可以使平衡配重同时放在多个平衡平面上，并减少轴承振动。Xu 等［6］采用同步电流降低的方法，提出了可变相位陷波反馈，可在线识别转子不平衡，通过离散的附加重量补偿转子不平衡和抑制谐波振动。运侠伦等［7］建立了动力学模型，采用有限元法对模型进行修正，抑制了主轴-转子系统不平衡引起的振动，提高了平衡效率。王仁超等［8］针对砂轮-电主轴系统的在线动平衡需求，设计开发的电磁式自动平衡头降低了加速度幅值。 Liu 等［9］为了解决磁悬浮轴承支承的刚性转子系统的不平衡振动问题，采用自动平衡方法有效抑制了转子系统的不平衡振动。Xu等［10］为了提高转子自动平衡的控制效率和平衡精度，提出了一种模糊自动校正的单神经元PID 控制方法。Ye 等［11］提出了一种基于动态相似比例模型的无试重平衡方法，消除了原型系统的重量测试过程。Jiang 等［12］将参数化时频分析和全息平衡法相结合，确定了转子的不平衡量和不平衡角。Zhang等［13］建立了振动响应与不平衡激励之间的数学模型，设计了动平衡模型的仿真程序。Larios 等［14］提出了一种基于代数识别技术的在线标识符方法，使2 个平衡盘可以同时平衡4 种振动模式。

综上所述，关于旋转机械在线动平衡的研究已经取得了一定成果，但是如何能够针对自动平衡装置进一步提高在线动平衡的质量和效率仍是目前亟待解决的问题。笔者主要围绕主轴系统的在线动平衡开展研究，在不平衡产生机理及动平衡调控方法的基础上，建立在线动平衡质量补偿策略优化数学模型，优化质量块的移动方案，从而实现更高精度、更高效的在线动平衡。

1 在线动平衡质量补偿优化模型

1.1 在线动平衡原理

主轴在线动平衡系统主要是通过平衡头内配重块的移动来补偿不平衡质量。计算机将控制命令传给控制装置，控制平衡头内部微型电机转速。振动传感器连接到主轴外壳，检测主轴转速脉冲信号并传递振动信号到控制单元，当传感器监测到不平衡振动量大于设定的阈值时，从而使配重块转动，直至2 个配重块产生的离心合力的大小与不平衡力相等，方向与不平衡力相位相反，这时可以认为主轴达到了平衡状态。

为了将动平衡原理表现的更直观，可将动平衡原理模型进一步简化，将2 个配重块等效为2 个质点，且其旋转半径相同。在动平衡装置中，2 个配重块的质量和体积一般都是相等的。建立如图1 所示的双配重块平衡力学模型。图中的A，B 小球代表2个配重块，C 小球代表主轴的固有不平衡量。当主轴平衡时，得到

其中：F为主轴的固有不平衡量；FA为配重块A 产生的质量补偿量；FB为配重块B 产生的质补偿量；mA为配重块A 的质量；mB为配重块B 的质量；ω为主轴的转速；φ为2 个配重块的夹角。

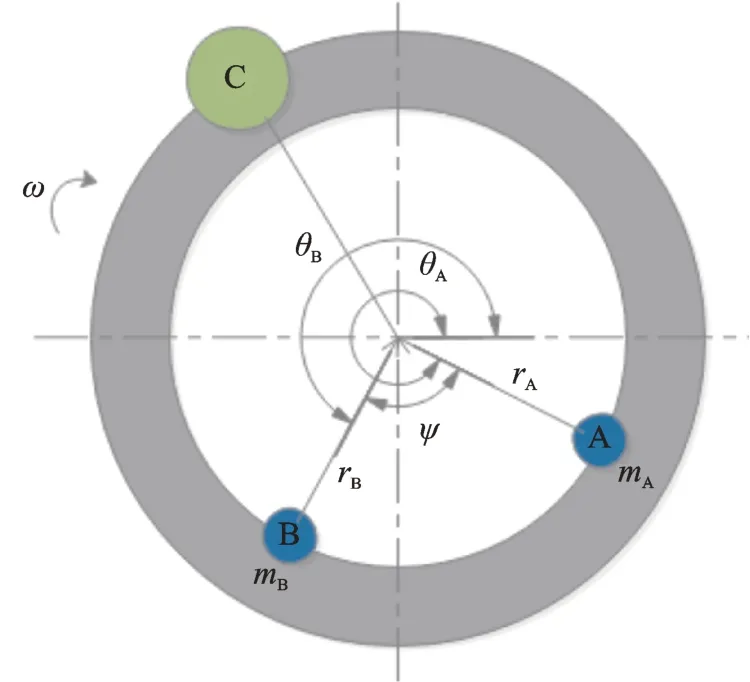
图1 双配重块平衡力学模型Fig.1 Balance mechanics model of double counterweight

1.2 优化模型

质量补偿策略优化就是对2 个配重块的移动策略进行优化。首先，对配重块的补偿策略进行数学建模；其次，在Matlab 中利用遗传算法优化出配重块的相位。图2 为质量补偿策略优化流程。

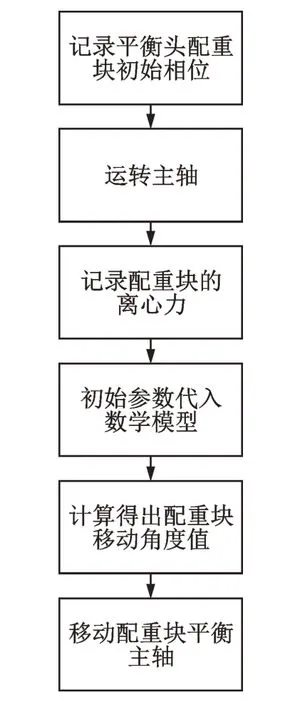
图2 质量补偿策略优化流程图Fig.2 Quality compensation strategy optimization flow chart

在对主轴进行平衡时，主轴残余不平衡力的表达式为

其中：P为主轴平衡后的残余力；W为主轴的固有不平衡力。

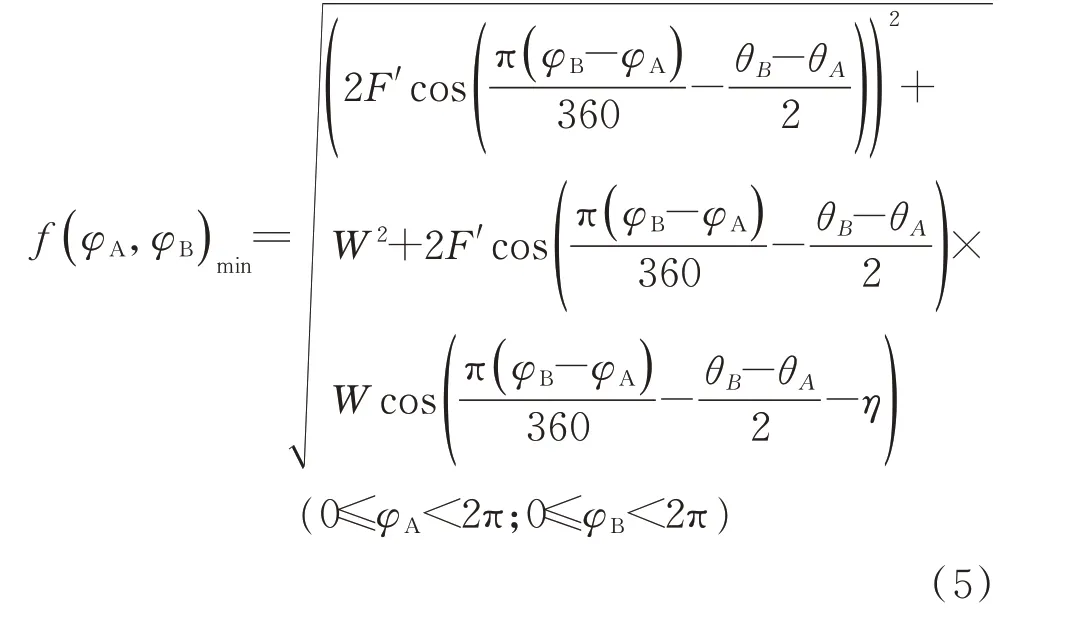
在对2 个配重块的移动策略进行模拟时，需要对配重块在极坐标下移动的角度进行建立数学模型。根据平衡原理，2 个配重块移动的角度φA和φB为优化变量，主轴的残余不平衡力为优化目标。数学模型为其中：φA和φB为平衡头中的配重块A 和B 在极坐标下的移动角度值；θA和θB为配重块A 和B 在平衡头中的初始相位；F'为配重块A 和B 离心力的合力；η为主轴固有不平衡量的相位；W为主轴的固有不平衡力。

通过计算机随机生成N组（φA，φB）作为第1 次迭代的初始解，即初始种群；计算第m次迭代时第j组初始解所对应的f(φA，φB)j，m，并根据f(φA，φB)j，m的大小进行选择淘汰，其中：j=1，2，…，N；m=1，2，…，H；H为预设迭代次数。

第j组初始解可以被保留的概率为

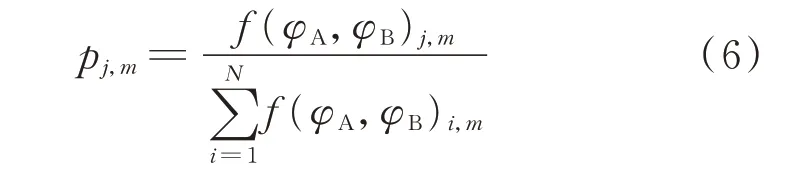
其中：f(φA，φB)i，m为第m次迭代时第i组初始解所对应的f(φA，φB)；i=1，2，…，N。

每个pj，m的累积概率qj，m为

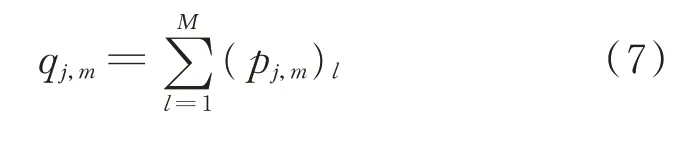
其中：(pj，m)l为第m次迭代时第l次计算得到的被保留概率；M为第m次迭代时N组初始解中被保留概率的总次数；r为在［0，1］区间内产生的一个随机数，若r＜qj，m，则保留第m次迭代时 第j组的初始解，否则，淘汰第j组的初始解。

图3 为模型通过遗传算法的迭代求解流程。将保留的第m次迭代时的第j组初始解转换为二进制，通过交叉变异得到最新解。将得到的最新解作为第m+1 次迭代的初始解，令m=m+1，并进行迭代计算，将H次迭代后的结果作为最终解。将最终解转换为十进制输出，作为优化后的2 个配重块在极坐标下的移动角度值（φAH，φBH）。

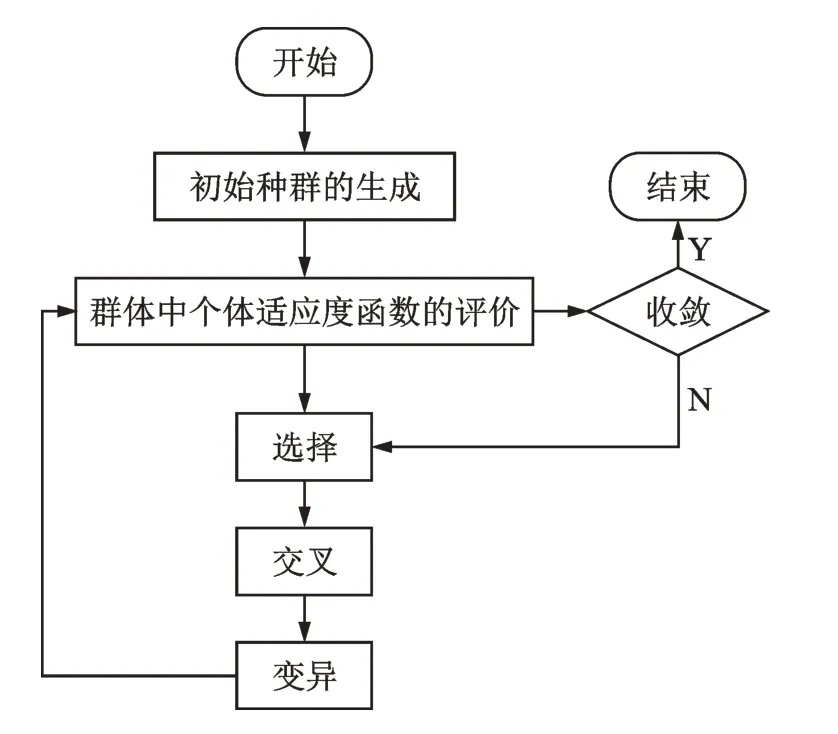
图3 迭代求解流程Fig.3 Iterative solution process

2 在线动平衡质量补偿优化实验

2.1 主轴系统动平衡实验平台搭建

在线动平衡实验平台由电机、主轴、计算机控制单元、振动传感器和电磁滑环式平衡头等组成。计算机将控制命令传给控制装置，控制平衡头内部微型电机转速。传感器与主轴外壳相连，检测主轴的转速信号以及振动信号，并传递振动信号到控制单元，调整平衡头内部质量块。图4 为实验平台示意图。

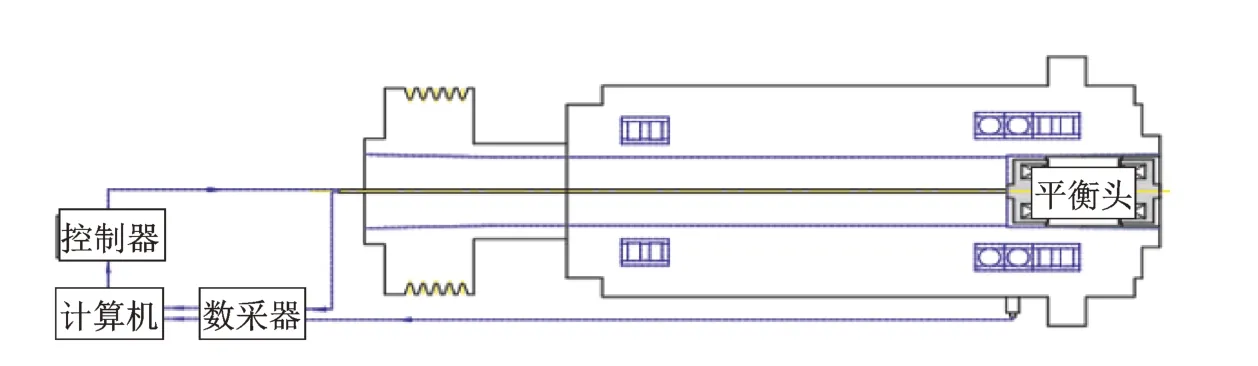
图4 实验平台示意图Fig.4 Schematic diagram of the test platform

2.2 主轴在线动平衡策略优化模拟实验

初选1.0，1.5，2.0，2.5，3.0 和3.5 kr/min 6 种不同的转速对主轴的不平衡进行研究。在没有负载的实验条件下，在主轴的前端加不平衡量来模拟主轴的不平衡。利用动平衡装置对主轴进行平衡，通过对比主轴平衡前后的振幅来验证笔者所提出的方法。将提出的配重块移动策略应用于平衡实验中，以优化平衡的调节方式对主轴进行平衡。该过程用于检验优化后得出的配重块位置的合理性，并将得到的平衡效果进行对比。

在 主 轴 前 端 分 别 添 加16.5，22.0 和27.5 g·mm的不平衡量，初始相位分别为180°，120°和240°。为了避免主轴在启动时振幅过大，则把配重块的初始相位设定为0°和180°。应用质量补偿优化方法计算出平衡装置的配重块相位如表1 所示。

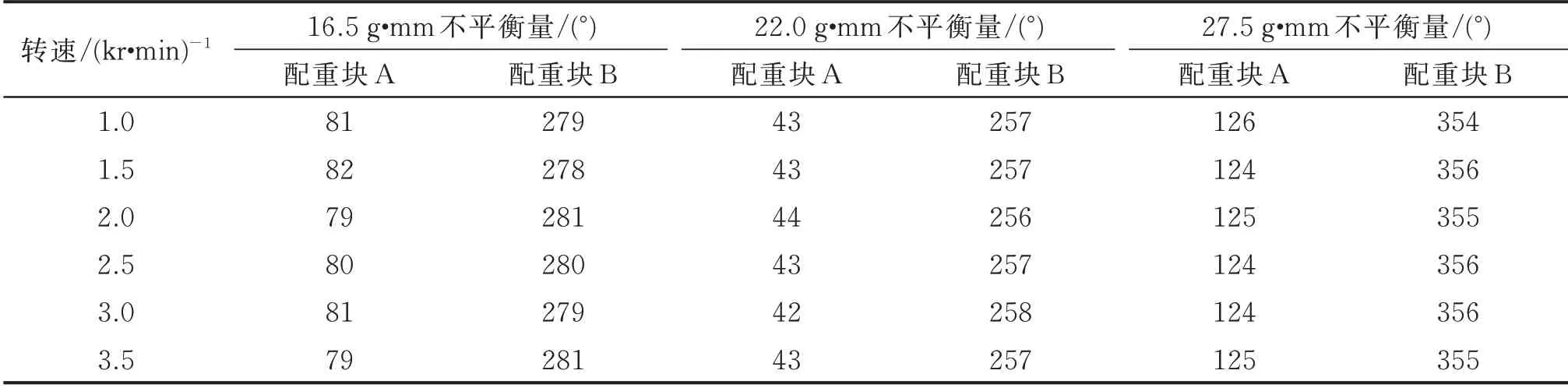
表1 优化后平衡装置的配重块相位Tab.1 The optimized phase of the counterweight block of the balancing device

由表1 可以看出，在不同速度、质量及相位下，每次实验时配重块应达到的平衡相位。在同一相位时，不同速度下的配重块的相位几乎都相等，这是由于配重块的质量远大于不平衡质量，在很小的范围内便可以平衡不同转速下的不平衡。质量补偿优化后的位置在理论上是配重块的最优相位，但由于实际工况复杂，在动平衡装置的自动平衡下，配重块位置达不到相应的相位，从而达不到上述精度。在手动调节模式下，完全可以使配重块达到相应的相位。

平衡前的不平衡力如图5 所示。可以看出，随着转速的上升，不平衡力也随之增大，最大的不平衡力为82.31 N，产生于外加27.5 g·mm 的不平衡量，转速为3.5 kr/min。

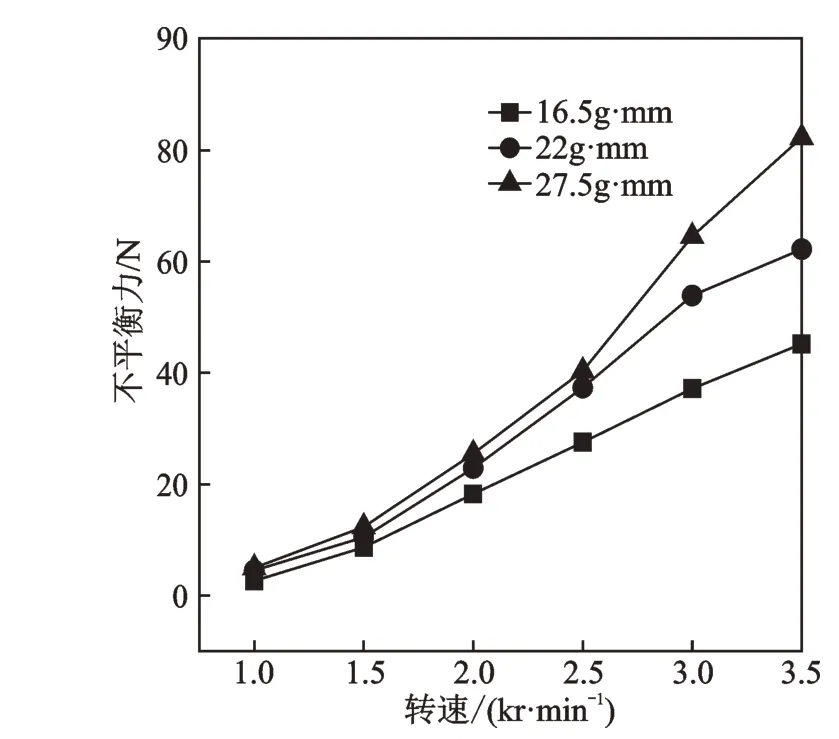
图5 平衡前的不平衡力Fig.5 Unbalance force before balance

图6 为平衡后的残余力。可以看出，在转速相对较高时，平衡装置的平衡能力下降，残余力大幅度增加。最小残余力在不平衡量为22 g·mm、转速为1.0 kr/min 时产生，其大小为0.07 N。最大残余力达到了4.9 N，在不平衡量为22 g·mm、转速为3.5 kr/min 时产生。残余力的变化表明调控策略优化得到的配重块的相位是正确的，可以有效平衡主轴。

图6 平衡后的残余力Fig.6 Residual force after balance

3 主轴在线动平衡优化对比实验

用动平衡装置对上述实验条件进行实验，可以得到3 种不同的外加不平衡量在平衡前后的振幅，如图7 所示。由于实验平台共振，在转速为1.5 kr/min 时，振幅波动较大。当转速为1.5 kr/min、不平衡量为27.5 g·mm 时，平衡前的最大振幅为26.98 μm。当转速为1.0 kr/min、不平衡量为16.5 g·mm 时，最小振幅为4.15 μm。当转速为3.0 kr/min、不平衡量为27.5 g·mm 时，最大平衡率为66%，平均平衡率为57.99%。

利用质量补偿优化方法对主轴进行优化平衡，初始条件与未优化平衡的条件相同，当动平衡装置中的2 个配重块准确达到质量补偿优化模型计算出的相位时，可以认为主轴达到了平衡。

未优化平衡时，2 个配重块的相位分布在优化平衡的相位周边，但是没有优化平衡的相位精确，且优化平衡时2 个配重块合力的相位与不平衡质量的相位呈180°，这就最大限度地抑制主轴的不平衡。未优化平衡与优化平衡的配重块相位属于合理的区间，2 个配重块的相位在3 种不同的外加不平衡量和转速的情况下，相位的波动更小，相位更精细。从实验对比得知，计算出的相位会更加合理。未优化平衡与优化平衡最大的区别体现在主轴的振动幅度上。图8 为优化平衡前后的振幅对比。可以看出，在低转速时，主轴的振动幅值较低，不管是优化平衡还是未优化平衡，都未能使主轴的振幅有较大的下降，但随着转速的上升，主轴的振动幅值大幅上升。未优化平衡时，主轴的幅值已经下降了一部分，但经过优化平衡，主轴的振幅较未优化平衡又有所下降，平均下降20.60%，最高下降29.64%。

图7 3 种不同的外加不平衡量在平衡前后的振幅Fig.7 Three different applied unbalance amplitudes before and after equilibrium

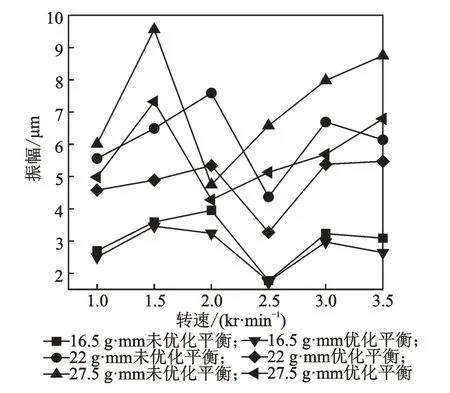
图8 优化平衡前后的振幅Fig.8 Amplitude before and after balance with optimized balance

图9 为优化平衡前后质量块移动步数。平衡装置的质量块移动一步需要5 s。图10 为未优化平衡时间与优化平衡时间的比较。由于设备老化和实际工况等原因，不管是未优化平衡还是优化平衡，时间都远超出平衡的理论时间。未优化平衡时，在转速为3.5 kr/min 时，平衡时间最长需要45 s，移动9 步；而优化平衡时间在转速为3.0 kr/min 时，最长需要30 s，移动6 步。平衡时间平均下降34.67%，最高可下降52.78%。

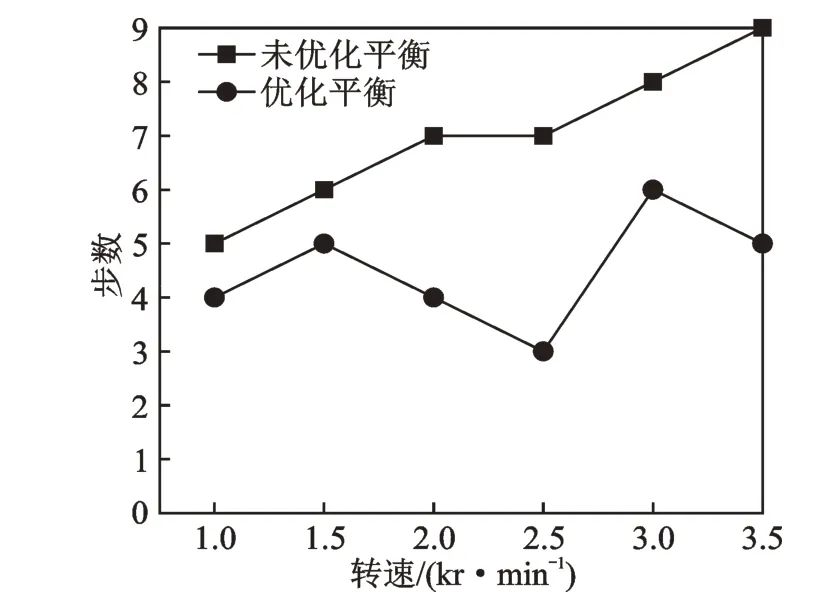
图9 质量块移动步数Fig.9 Number of mass movement steps

图10 平衡时间Fig.10 Balance time

用主轴在线动平衡装置来验证提出的质量补偿优化方法。实验结果表明：配重块的质量补偿优化方法提高了主轴的平衡精度，相比于未优化平衡，动平衡装置在优化平衡下可以使主轴的振动幅值进一步下降，平衡时间减少；精确移动配重块的相位，可以降低在未优化平衡下的振动幅值。

4 结束语

主轴系统的在线动平衡质量补偿策略通过建立优化模型、改变平衡头质量块的移动方式，准确得到配重块的相位，从而有效提高了平衡精度和效率，降低了平衡时间。通过实验可知，主轴在线动平衡装置优化后，主轴的振幅较未优化平衡平均下降20.60%，最高下降29.64%，平衡时间平均下降34.67%，最高下降52.78%。基于遗传算法的在线动平衡质量补偿优化方法为进一步实时降低主轴系统振动、提高加工精度和效率奠定了理论基础。