风力机轴承实时剩余寿命预测新方法∗

吕明珠， 苏晓明， 刘世勋， 陈长征

（1.沈阳工业大学机械工程学院 沈阳，110870）（2.辽宁装备制造职业技术学院自动控制工程学院 沈阳，110161）（3.中国质量认证中心（沈阳）北方实验室 沈阳，110164）

引 言

滚动轴承作为风力发电机组传动系统中的易损件之一，一旦发生故障需要耗费大量的时间和成本进行检修［1］。若能对风力机轴承的运行状态进行适时监测和寿命预测，变事后维修为视情维护，可有效避免重大安全事故的发生和降低运维成本，提高风力发电机组的安全性、可靠性和可利用率［2］。

目前，常用的寿命预测方法大体可分为基于数据驱动的方法和基于模型的方法［3-4］。基于数据驱动的方法是通过机器学习建立运行数据与退化状态之间的联系，无需研究退化机理，也无需大量的先验知识。Wang 等［5］采用主成分分析方法得到退化特征，建立了基于反向传播神经网络的预测模型，实现了对滚动轴承状态趋势的预测。Shivani 等［6］使用整体经验模式分解策略计算时域特征，同时构造支持向量回归模型对滚动轴承的健康状态进行预测。由于机器学习方法对历史数据依赖性较强，因此该预测方法存在一定的局限性，不合适解决风力机轴承这种长期处于交变载荷作用下且受各种不确定因素影响的预测问题。基于模型的方法是通过建立数学模型来描述整体衰退趋势，从而进行剩余寿命预测，并依据观测结果对模型参数实时更新。该方法可以充分挖掘经验知识和观测数据之间的对应关系，得到较为可靠的寿命预测结果。阙子俊等［7］利用振动信号建立特征指数，构建出非线性状态空间模型，并采用无迹卡尔曼滤波（unscented Kalman filter，简称UKF）算法对模型参数进行更新，实现了轴承性能评估和剩余寿命预测。由于UKF 需要状态变化服从高斯分布，因此不利于在实际应用中推广。文娟等［8］基于粒子滤波（particle filter，简称PF）和UKF，得到无迹粒子滤波算法，实现了滚动轴承的剩余寿命预测。该方法虽然解决了UKF 受高斯分布的限制和PF 中的粒子退化问题，但选择有效值作为退化指标对周期性冲击敏感度低，且易受到外界干扰的影响。

笔者提出了一种风力机轴承实时剩余寿命预测方法，该方法包含退化指标提取和剩余寿命预测2个步骤。退化指标提取是利用包络谐噪比对原始信号的早期退化点进行检测，以便于适时启动寿命预测机制，有效节约计算资源。寿命预测是通过历史数据进行退化模型构建，利用UPF 算法使重要性分布函数总能体现最新的观测信息，从而加强了粒子的跟踪能力，使模型参数不断更新，显著提高了剩余寿命的预测准确度。

1 理论基础

1.1 包络谐噪比算法简介

EHNR 是指对数据样本做包络处理后谐波能量与噪声能量的比值［9］，其大小不仅可以表征故障的强弱，还可以充分反映故障引起的周期性冲击，具有敏感性和鲁棒性，是一种用于滚动轴承故障诊断和预测的新指标。利用其敏感性可以检测轴承的早期微弱故障，利用其鲁棒性可以预测轴承退化趋势和剩余寿命。由于无需先验知识，有利于实现故障特征的自适应提取。

设任意时间序列x(t)有n个数据样本，每个样本有m个采样数据，即首先，对x(t)做Hilbert 变换，计算公式为

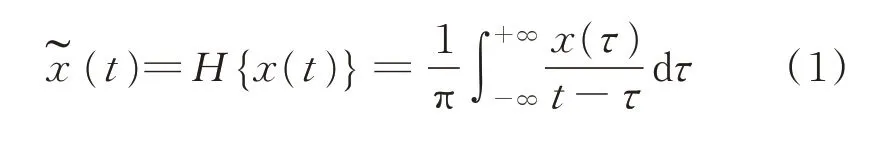
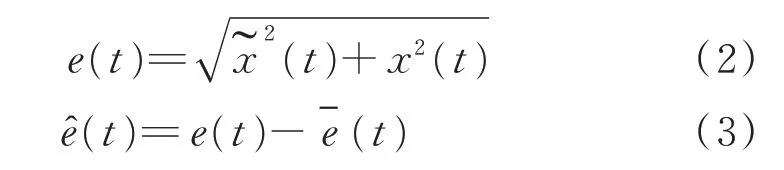
其中：e(t)为包络处理后的时间序列为均值；ê(t)为去除直流分量的新时间序列。

其中：τ为自相关函数的时间滞后量。

最后，确定原始信号的自相关函数在时间滞后域中的最大位置，即EHNR 定义为

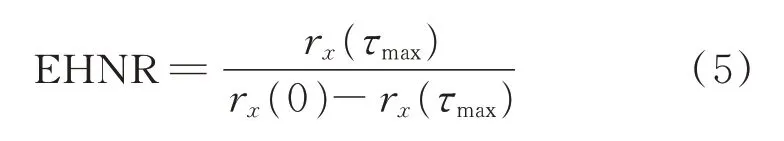
其中：τmax为rx(τ)自相关函数的最大位置为最大位置对应的幅值；rx(0)为包络总能量。

1.2 无迹粒子滤波理论

传统PF 算法是以贝叶斯理论为基础，通过观测数据对系统状态的概率密度函数（probability density function，简称PDF）进行估计［10］。

设离散时间序列在tk=kΔt时刻的状态方程和观测方程形式为

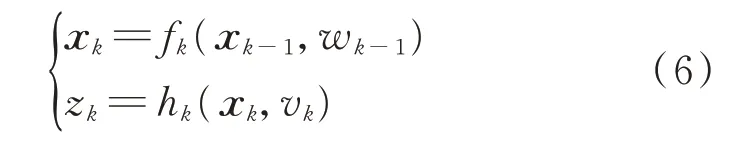
其中：xk为系统在tk时刻的状态；fk为系统状态传递函数；wk为系统噪声；zk为系统在tk时刻的观测值；hk为系统观测函数；vk为观测噪声。

后验概率密度为

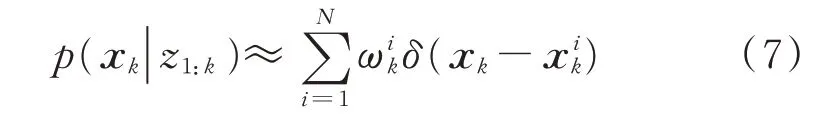
其中：p(⋅)为概率分布函数；δ(⋅)为狄拉克函数为粒子权重。

为了维持粒子的跟踪能力，需要对粒子和粒子权值不断更新，即重要性采样。由于直接从PDF 中采样较为困难，通常采用序列重要性采样（sequential importance sampling，简称SIS）算法，以一个先验概率近似代替PDF，如式（8）所示

其中：q(⋅)为重要性密度函数。

近似代替虽能简化计算，但容易使PF 算法陷入粒子退化问题，从而导致估计结果发散。UPF 使用UKF 来构造粒子滤波的重要性采样分布，将最新的观测信息融入重要性分布函数，加强了粒子的跟踪能力，提高目标跟踪的精度。UPF 算法步骤如下。

1）初始化。当k=0 时，从初始分布采样M个粒子生成原始粒子集且每个粒子对应的权值系数1，2，…，M；当k＞0 时，令k=k+1，经迭代得到一组新的粒子集1，2，…，M}。

2）重要性采样。用UKF 算法计算每一个粒子的均值和协方差矩阵，得到和根 据 高 斯分布得到重要密度函数中的采样粒子根据当前新测量值依据式（9）更新各粒子权值

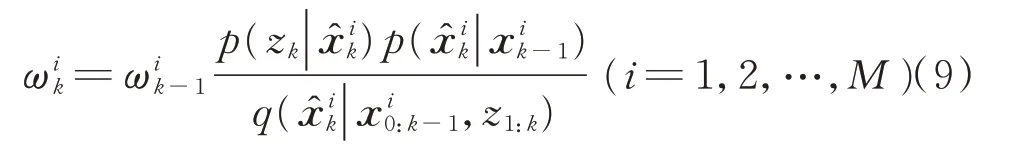
其中：下标0：k-1 表示0～k-1 时刻；1：k表示1～k时刻。

按式（10）进行归一化处理

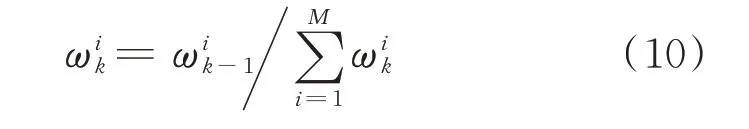
3）重采样［11］。按权值高低重排粒子，剔除权值较小的粒子，复制权值较大的粒子，增加有效粒子的数量。计算，若Neff＜Nthr（其中：Nthr为阈值，一般取M/3），则说明粒子已经严重退化，需要重采样。目前，常用的重采样算法有随机重采样、系统重采样和残差重采样，算法将处理后的粒子映射为等权重的M个粒子。

4）输出状态估计值和协方差矩阵，即

5）返回步骤2 重复以上步骤，直至满足终止条件。

2 风力机轴承的剩余寿命预测方法

风力机轴承的整个服役寿命可分为正常期、退化期和失效期3 个阶段。当轴承处于失效期时，无法可靠工作，必须及时维护或更换。因此，前2 个阶段的运行状态监测具有实际意义，而剩余寿命预测是从轴承进入退化期开始估计。通常振动信号对轴承的退化演变较为敏感且便于采集，故笔者选择振动信号提取退化指标。

EHNR-UPF 方法流程图如图1 所示。在对具体服役轴承进行剩余寿命预测时，首先要计算原始信号的EHNR，根据报警阈值判断是否进入退化期。若已开始退化，从监测到的早期退化点开始，利用UPF 方法结合退化模型和测量数据来更新模型参数，并依据EHNR 趋势特征评估故障的发展阶段，实现剩余寿命预测。

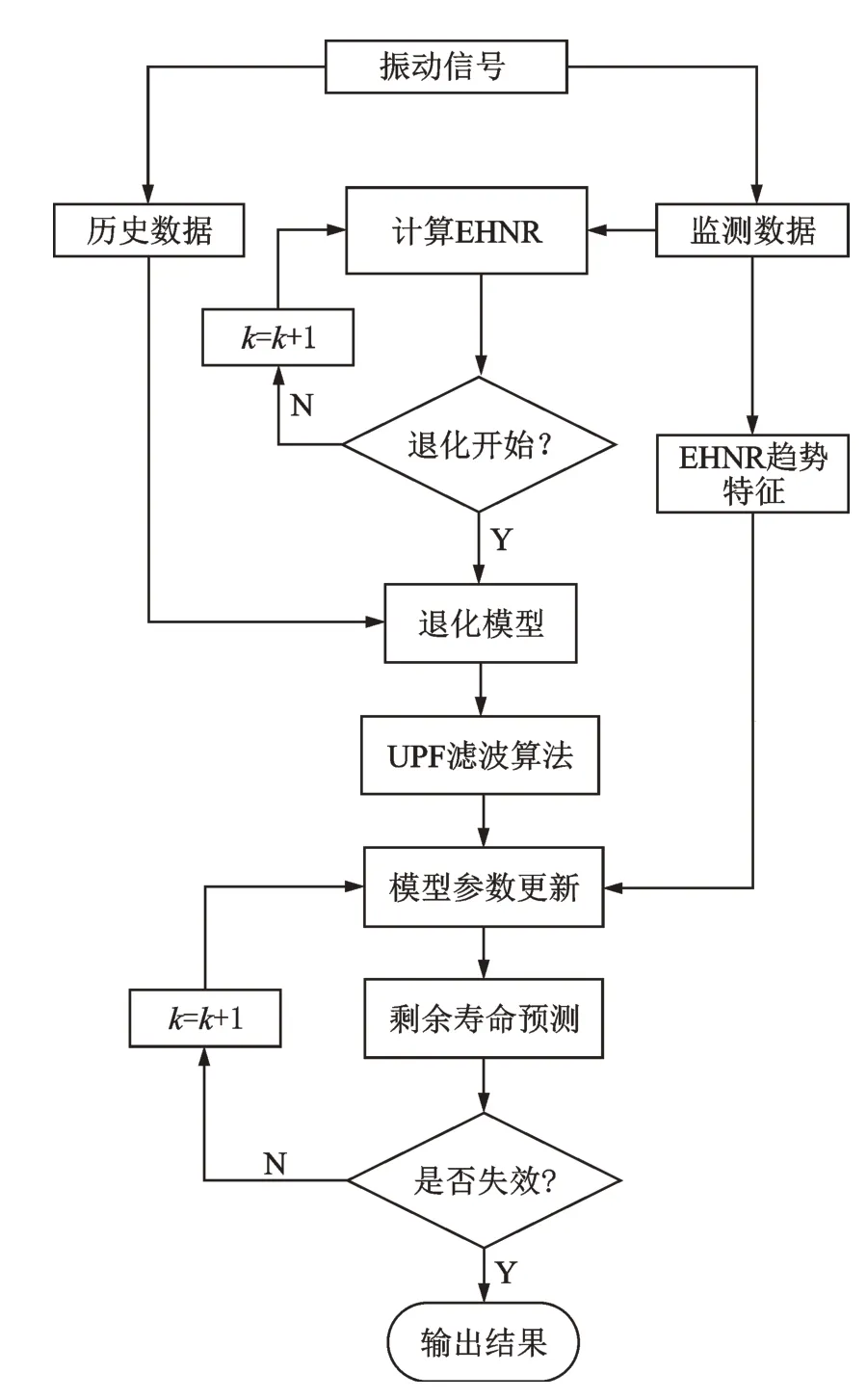
图1 EHNR-UPF 方法流程图Fig.1 Flow chart of EHNR-UPF method

2.1 早期退化检测

通常轴承处于正常期的时间比较长，EHNR 趋于平稳且数值较小，此时没有必要启动剩余寿命预测机制；而当轴承进入衰退期后，EHNR 会产生剧烈波动且持续增长。因此，监测早期退化的起点、适时启动剩余寿命预测预警工作，不仅可以节约计算资源，还能有效提高预测的准确度。

确定轴承进入退化期的报警阈值需要计算轴承处于正常期时相对稳定EHNR 的均值μ和标准差σ。根据高斯分布的4σ准则［12］，μ±4σ区间涵盖了99.99%的数据，超出这个区间的数据则为异常点。为了消除随机误差的影响，避免产生误报警，笔者引入多点触发机制来判断轴承的退化起点，即当监测到EHNR 连续l次（笔者l取5）超过异常阈值时，则认为轴承已开始进入退化期。

2.2 退化指标提取

由于EHNR 曲线通常呈振荡上升趋势，直接取其实测值不利于评估轴承退化的不同阶段，因此采用局部加权回归散点平滑法［13］拟合一条趋势性曲线作为退化指标。

对于指定窗口范围的每一个点xi（设窗口内有N个点，则0 ＜i≤N），其权值函数为

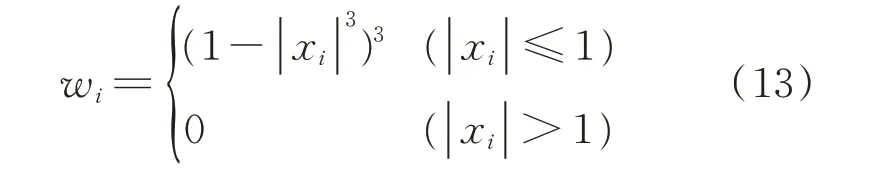
对应于原数据x和y的拟合方程ŷ=ax+b中，斜率a和截距b定义为

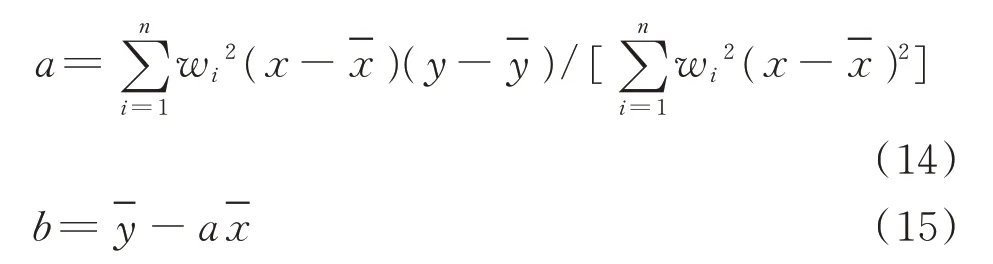
2.3 退化模型

通过对历史轴承退化期内退化指标数据的拟合分析发现，双指数模型能较好地反映轴承的退化趋势。因此，建立轴承的退化模型为

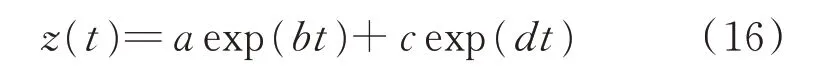
其中：z(t)为时刻t对应的退化性能趋势指标；a，b，c，d分别为模型待定参数。

根据轴承的退化模型，设观测值zk与状态值xk存在线性关系，得到其状态参数更新方程和观测方程为

其中：N(0，σ2)为系统状态方程的高斯白噪声；vk为观测方程的随机噪声。

利用当前观测值和UPF 算法更新式（17）中的4个状态变量，并预测下一时刻的退化指标，从而实现对轴承退化状态的实时评估。

2.4 剩余寿命预测

利用UPF 算法更新状态方程和观测方程参数至t时刻，依据退化模型可以估计t+p时刻的状态为

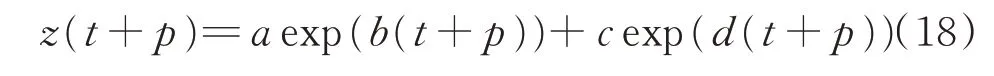
剩余寿命研究的目的是得到当前t时刻剩余寿命概率分布［14］，计算使不等式（19）成立的p值，记录p的最小值为t时刻预测的轴承剩余寿命，即可近似t时刻的剩余寿命概率分布

其中：threshold 为失效阈值。

另外，由于风力机轴承性能退化速度易受运行过程中不确定因素的影响，为了表征预测结果的差异程度，采用相对误差来表示其中：err(m)为轴承在第m个监测周期的寿命预测；

3 实例分析

3.1 实例说明

为了验证笔者所提出算法的有效性，以某风电场2.0 MW 风机采集的风力发电机前轴承振动数据为例进行验证。采集频率为25.6 kHz，每次采样长度为2560，采样间隔为10 min，持续跟踪467 h 至失效（约为20 d）。发电机前轴承测试现场照片如图2所示。

图2 发电机前轴承现场测试照片Fig.2 The test photo of front-end bearing of generator

图3 为轴承全寿命周期振动信号。可以看出，轴承经历了一段很长的正常工作期后开始出现退化，一旦进入退化阶段，轴承的振动信号幅值迅速增大直至失效。

图3 轴承全寿命周期振动信号Fig.3 The whole life cycle vibration signal of the bearing

3.2 剩余寿命预测与对比分析

轴承全寿命的EHNR 值如图4 所示。可以看出，轴承全寿命发展历程可以划分为3 个阶段。定义图4 中EHNR 波动较小且比较平缓的阶段为正常期，这一过程大约为200 h；EHNR 有轻度波动且有明显上升趋势的阶段为退化期，笔者所提方法要先判断轴承是否进入退化阶段，利用μ+4σ设置报警阈值。为了消除随机噪声的干扰，定义连续5 个以上的异常点为退化起始点。结果表明，当t约为226 h 时，轴承开始退化，如图4 中黄色圆圈点所示。此后，EHNR 随着退化程度的加深而持续增大。当EHNR 超过1.0 时，此时t约为411 h，轴承已经不能可靠工作。如果未能采取有效维护措施，最终将导致轴承失效，将该阶段定义为失效期。

为了更好地描述轴承的健康状况，提取EHNR的趋势线，如图4 中蓝色曲线所示。该趋势线具有单调性、连续性、鲁棒性和持久性等特点，可以作为衡量轴承退化程度的特征指标。根据历史失效轴承数据，将该指标等于1.0 作为失效判定的条件（实际失效时间约为462 h）。

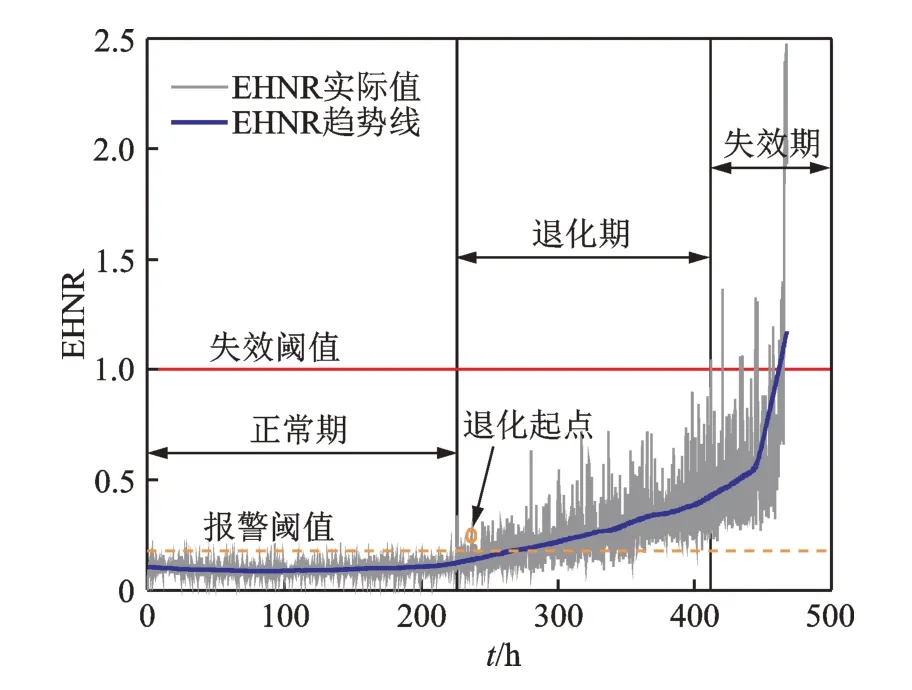
图4 轴承全寿命的EHNR 值Fig.4 The EHNR results of the whole life cycle of thebearing

轴承传统退化指标如图5 所示。均方根指标虽然能表征轴承退化过程的整体趋势，但对早期故障并不敏感，很难区分轴承退化发展的不同阶段。峭度值指标对较大的干扰冲击敏感，比EHNR 检测到的早期退化点晚（约为312 h），并随着冲击的密集这种敏感会逐渐失效。因此，笔者提出的特征指标能够更加准确地反映轴承的故障信息，便于进行后续的模型构建和寿命预测。

图5 轴承传统退化指标Fig.5 Traditional degradation indicators of the bearing

检测到轴承开始退化后，利用笔者提出的方法进行轴承剩余寿命预测。为了说明UPF 方法的优越性，将PF 方法作为对比，采用有效粒子数来衡量状态更新过程中粒子的退化程度。2 种方法的粒子数均选为1000 个，在状态估计过程中2 种方法的有效粒子数变化情况如图6 所示。从图6 可以看出，一旦迭代开始，2 种方法的有效粒子均出现不同程度的退化，但整体上看，UPF 方法的有效粒子数明显多于PF 方法的有效粒子数，这说明UPF 方法可以有效降低粒子的退化程度。

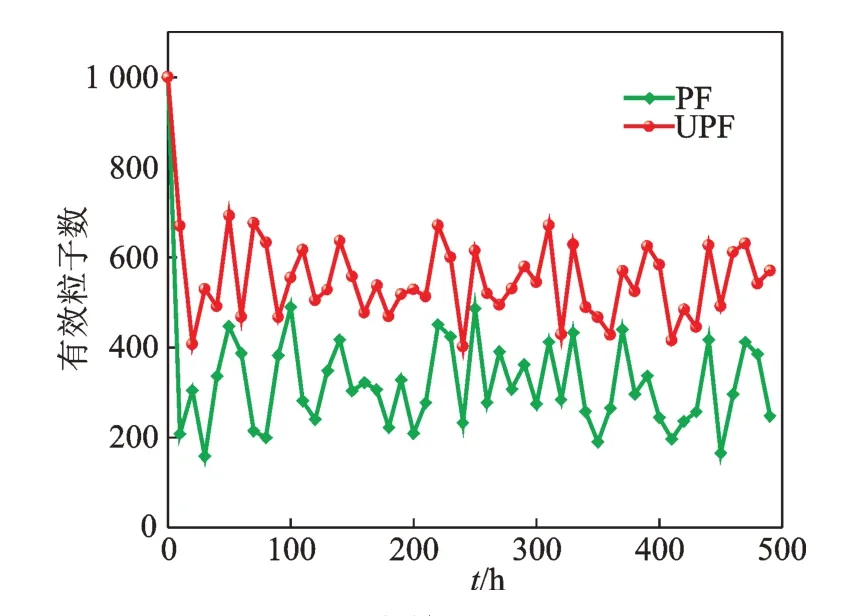
图6 有效粒子对比Fig.6 Comparison of the effective sample sizes

图7 和图8 分别为退化初期和退化末期的预测结果。图7（a）将预测起点设置为t=226 h（即退化起点），使用PF 方法预测到退化指标值超过失效阈值的时间为483 h，而真实的失效时间为462 h，因此其剩余寿命预测误差为21 h；而使用UPF 方法得到的预测时间为475 h，预测误差为13 h。图7（b）为预测结果的局部放大图。

图8 将预测的起点设置为t=411 h（之后进入失效期），从图8（a）可以看出，随着学习数据量的增加，2 种方法的预测结果均逐渐趋于真实值，但UPF方法的预测结果准确度仍高于PF 方法。图8（b）为预测结果的局部放大图。此时PF 方法预测轴承的失效时间为480 h，预测误差为18 h；而UPF 方法预测轴承的失效时间为472 h，预测误差为10 h。这是由于UPF 方法总能够将最新的观测信息融入粒子后续权重的更新过程，因而与实际状态产生的偏差较小，可有效避免大部分粒子权重过小而发生的退化，能够更好地估计系统的状态，故采用UPF 方法进行轴承剩余寿命预测可显著提高预测的准确度。

表1 为2 种方法在不同监测范围内的实际剩余寿命与预测剩余寿命之比，可以看出：①运行初期（周期1）的轴承处于相对稳定的状态，没有受到过多不确定因素干扰，但由于参与模型更新的数据点少而使相对误差较大；②运行中期（周期2～4）的轴承虽然受到各种外界不良因素的影响，但经过一段磨合期后基本处于稳定运行期，相对误差减小且波动不大；③运行后期（周期5）的轴承逐渐进入退化期，性能急剧劣化，由于退化速度过快而使相对误差又有增大趋势，但整体上看，UPF 方法的相对误差明显小于PF 方法。

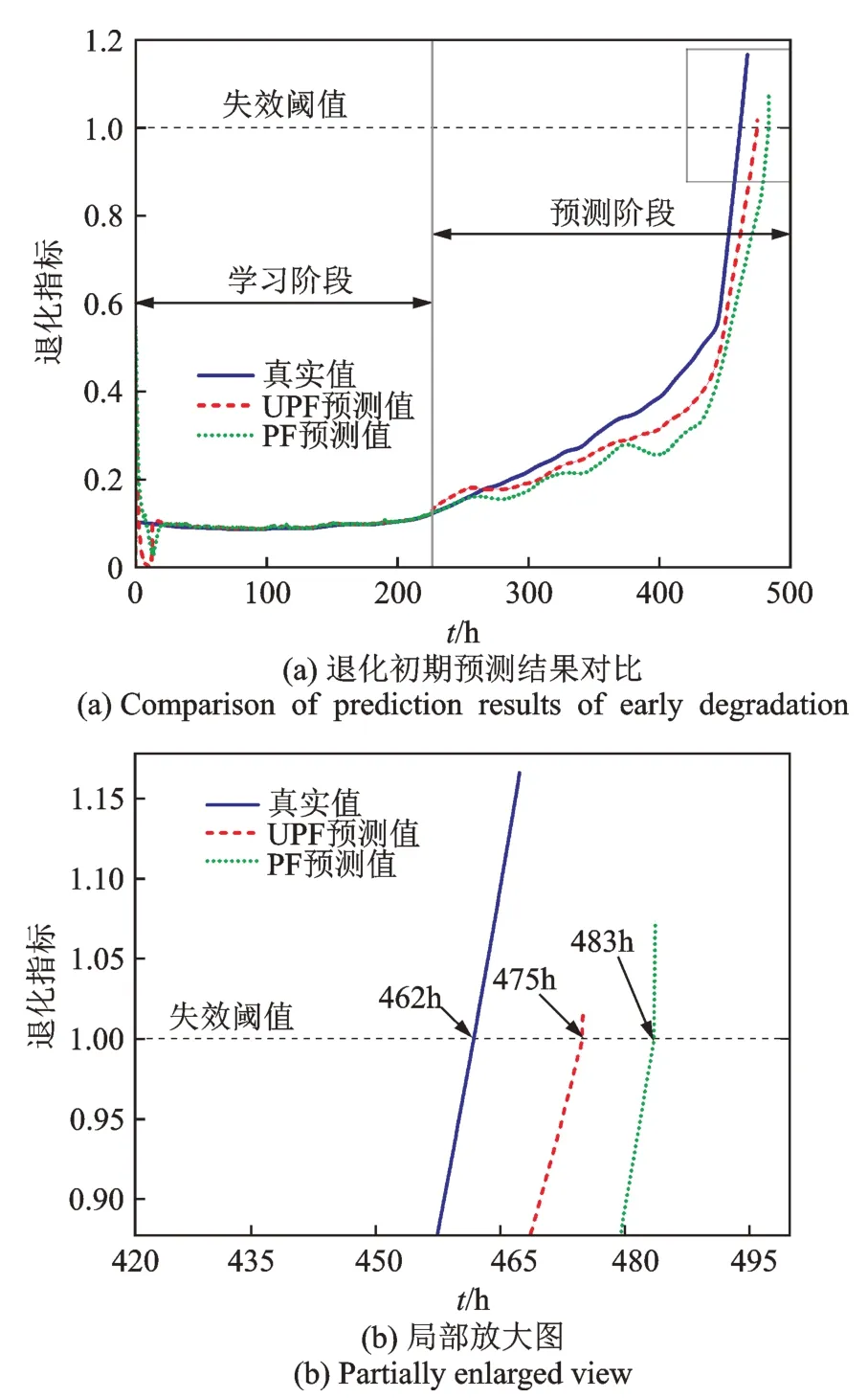
图7 退化初期的预测结果Fig.7 Prediction results of early degradation process

为了说明笔者提出的方法相比于其他寿命预测方法的优越性，选取了广泛使用的BPNN 和SVR 预测方法进行对比。模型均选用前226 h 的数据作为训练集，后236 h 的数据作为预测集。3 种寿命预测方法结果对比如图9 所示。其中：BPNN 的隐层数设为3，节点数设为8，学习率为0.01；SVR 采用径向基核函数，利用交叉验证法选择参数。从图9 可以看出，BPNN 和SVR 均没有得到有效的预测结果。这是因为BPNN 是一种局部搜索算法，当面对复杂非线性问题时易陷入局部最小值，从而导致网络训练失败。SVR 虽然可以解决非线性问题，但模型参数的选择对预测结果影响很大，从而导致预测结果不准确。

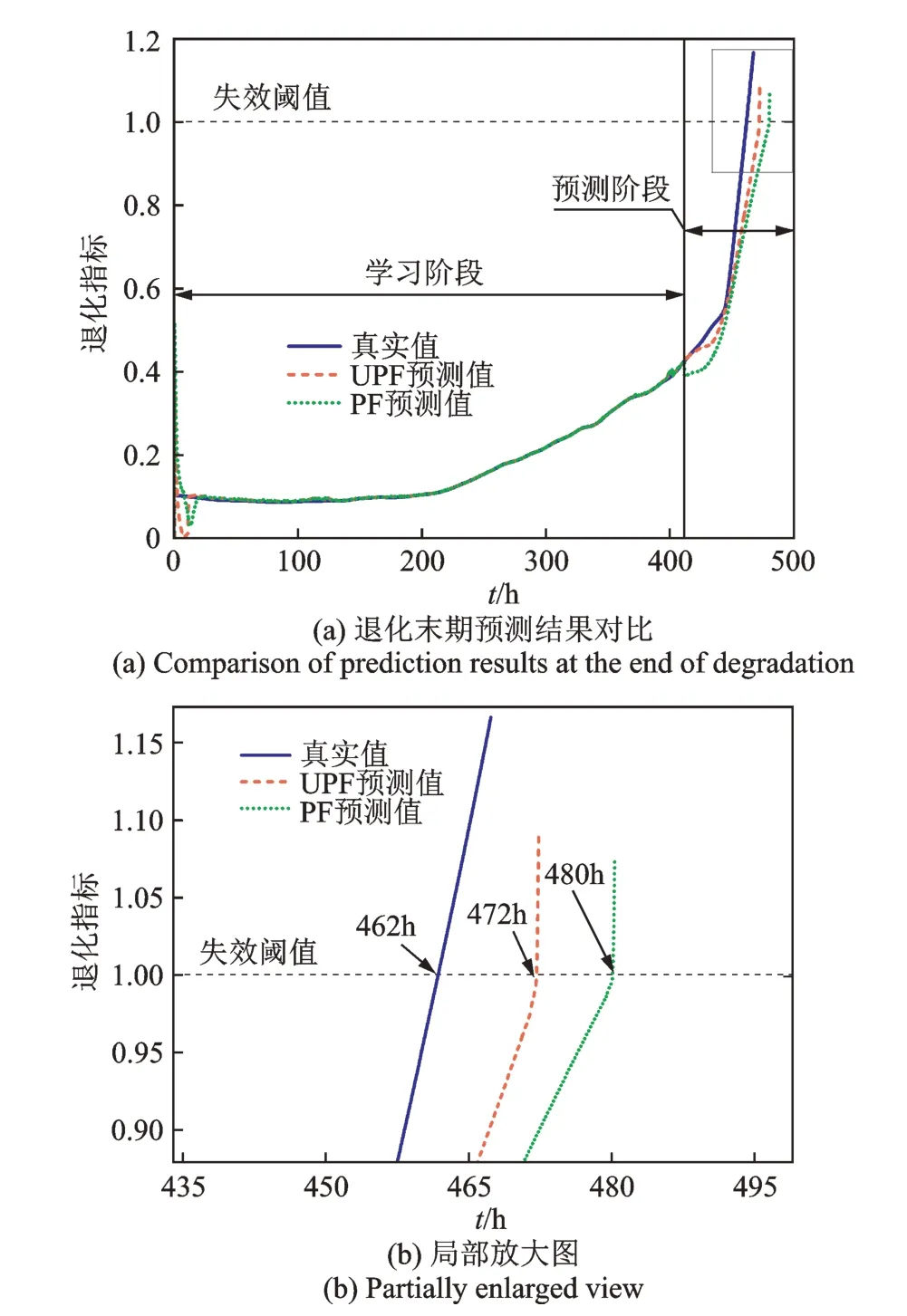
图8 退化末期的预测结果Fig.8 Prediction results at the end of degradation

表1 2 种方法的实际剩余寿命与预测剩余寿命之比Tab. 1 Comparisons of two approaches between actual and predicted remaining useful life

4 结 论

1）EHNR 值可以很好地反映出轴承故障冲击的周期性特征，与传统的有效值和峭度值指标相比，具有敏感性和鲁棒性双重特点，是一种可用于滚动轴承故障诊断与预测的新指标。

图9 3 种寿命预测方法结果对比Fig.9 Comparison of three life prediction methods

2）UPF 算法能把最新的观测信息融入粒子权值的更新过程中，从而有效降低粒子退化程度，并能根据不同时期的轴承运行数据实现退化模型的参数更新和状态估计。相比于传统的PF 方法，能显著提高预测的准确度。

3）提出的EHNR-UPF 风力机轴承剩余寿命预测方法与目前广泛使用的BPNN 和SVR 预测方法相比，具有良好的趋势性和较高的准确性，可用于风力发电机组轴承的状态监控和智能运维，为其健康状况管理和可靠性评估提供参考依据。