基于局部边缘判别投影的机械故障诊断方法∗

石明宽， 赵荣珍

（兰州理工大学机电工程学院 兰州，730050）

引 言

对旋转机械进行故障诊断时，为了获得可信度高的诊断结果，必须尽可能多的获取故障信息［1］。通常采用多个传感器进行多通道的监测，提取出多通道、多域的故障特征对故障进行全面描述［2］。这导致了大量的冗余信息和高度相关的信息形成了“维数灾难”，不仅加重了分类器的工作负担，同时也很难得到满意的诊断结果［3］。因此，对数据结构优化的数据降维问题进行研究，对于推动智能决策技术向工业大数据驱动的方向发展具有良好的促进作用。

局部保持映射（locality preserving projection，简称LPP）［4］是对传统拉普拉斯特征谱（Laplacian Eigenmap，简称LE）［5］嵌入进行线性化近似的结果，其继承了LE 算法保持样本局部邻域结构不变的特点，同时解决了样本外点学习能力不强的缺点。LPP 本质是无监督算法，忽略了有利于分类的判别信息，在投影之后会出现样本点重叠，分类时容易出现错分现象。线性判别分析（linear discriminant analysis，简 称LDA）［6］的 基 本 思 想 是 通 过 最 大 化Rayleigh 商的方式，实现类间散度最大的同时使类内散度最小，寻找一个最佳判别投影矩阵，从高维特征集中提取出最具有判别能力的低维敏感特征子集，使得同类特征聚集更紧密，异类特征更分散。这种基于Rayleigh 商的降维方法能够突出故障数据集之间的判别信息，在故障模式识别中具有一定的优势［7］。LDA 是基于保持全局结构信息的降维算法，忽略了特征集的局部几何结构信息，而局部几何结构信息更能反映数据的几何结构［5］，且LDA 容易产生小样本问题。针对上述问题，在LDA 的基础上，结合LPP 的基本原理，笔者提出一种局部边缘判别投影属性约简算法，以进一步提高LDA 的识别性能。LMDP 引入了局部类内相似度与局部类间相似度，不仅能够反映样本之间的近邻关系，而且能够反映类中心之间的近邻关系。为了避免在实际应用中可能出现的小样本问题，在低维嵌入过程中构建散度矩阵迹差形式的目标函数，同时加入正交化约束，以减小投影后特征分量之间的信息冗余。

基于上述分析，本研究对基于LMDP 的转子故障数据集降维方法进行研究，从海量数据中挖掘更充分的数据结构信息，为智能故障模式识别技术的发展提供了一种理论参考依据。

1 基于LMDP 的故障诊断方法

1.1 LDA 算法简介

设有M个训练样本X=［x1，x2，…，xM］∈RQ×M，且这M个训练样本被分为C类X1，X2，…，XC，每类含有n个样本。线性判别分析定义的样本类内散度矩阵、类间散度矩阵可分别表示为

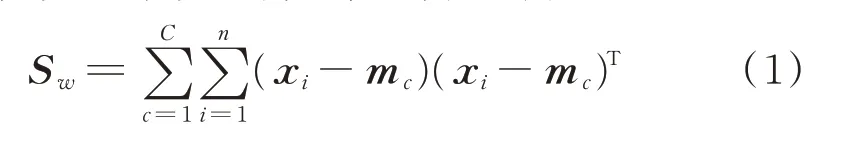
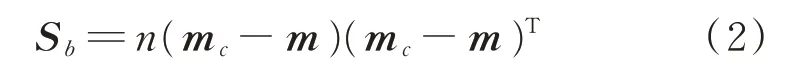
其中：mc为第c类样本均值；m为总体样本均值。

LDA 的目标准则函数为

1.2 LMDP 算法设计

1.2.1 基本思想

根据文献［8］，LDA 的散度矩阵Sb，Sw可等价表示为

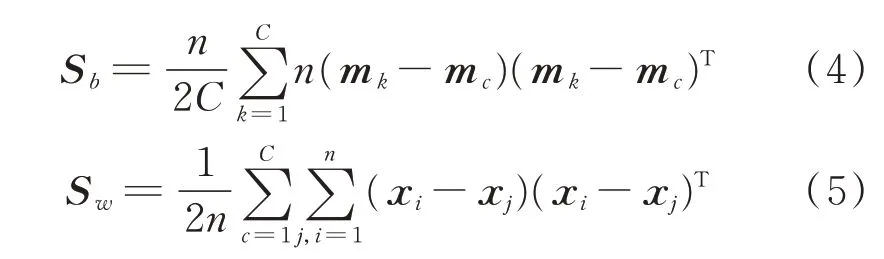
根据式（4），（5）可知，LDA 目标函数的实质是通过最大化异类中心点之间的距离，同时最小化同类样本点之间的距离，实现同类样本点相互靠近且异类样本点相互分离的目的。

LDA 是一种基于样本整体结构的属性约简算法，并不能描述样本之间的近邻关系，且容易产生小样本问题。针对LDA 的不足，LMDP 引入了同类样本之间的相似度权重来描述同类样本点之间的近邻关系；同时引入异类中心点之间的相似度权重来描述异类中心点之间的近邻关系；使相邻的异类之间离的更远，相邻的同类样本之间聚的更近，在低维空间中更好地保持了局部几何结构。

1.2.2 目标函数

对于数据分类，将相邻的类区分开比将相距较远的类区分开要困难的多，只要相邻的类的区分性好，那么与其他类将更容易区分和识别。因此，新的类间散度可定义为

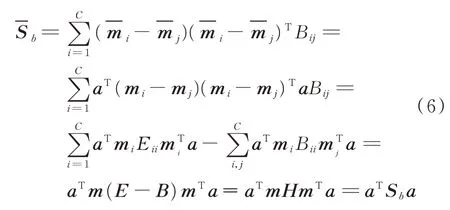
其中：C为样本类别个数为第i类样本投影后的均值为第i类样本均值；m=［m1，m2，…，mC］；E为对角矩阵，对角线元素Eii=为拉普拉斯矩阵；Sb为类间散度矩阵。

B为样本均值相似矩阵，其元素为

其中：N（mi）为类i的k1个近邻类组成的邻域；k1为相邻类的个数，即1≤k1≤C，本研究取k1=2；t为所有样本之间欧式距离均值的平方［9］。

根据LPP 算法的主要思想，高维空间中离的很近的点映射到低维空间后也应该离的很近［4］。因此，新的类内散度可定义为

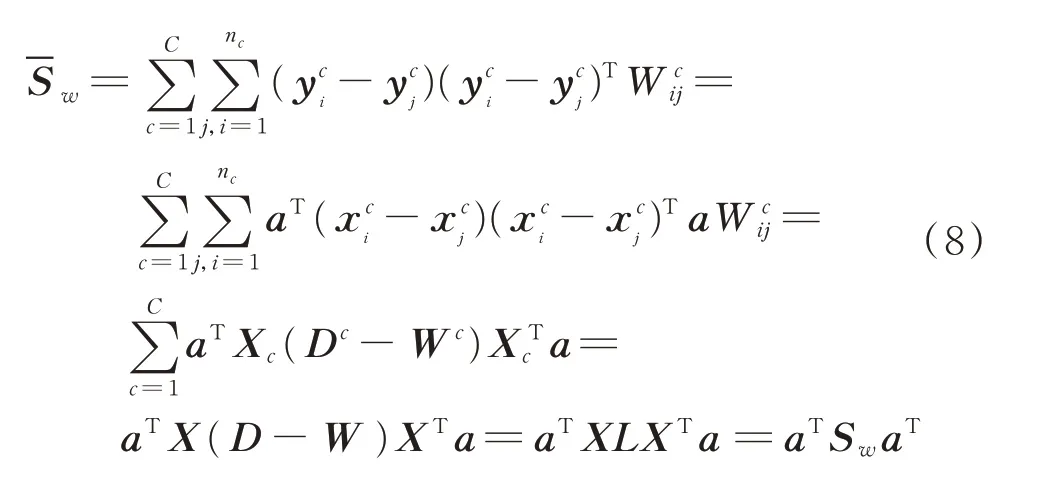
其中：nc为第c类样本的个数；Dc为对角矩阵，对角线元素为拉普拉斯矩阵；为类内散度矩阵

Wc为第c类样本的相似矩阵，其元素为

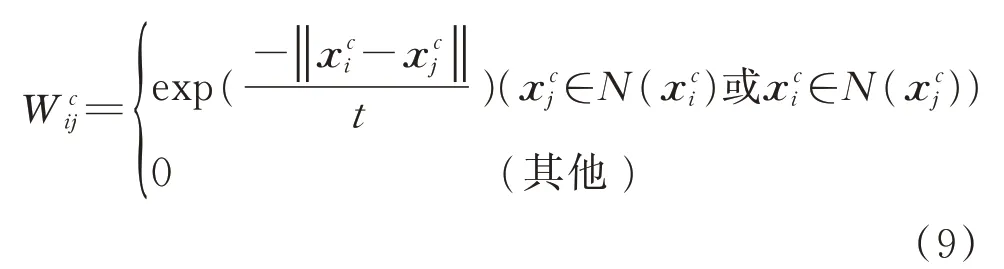
其中：N（xi）为xi的k2个近邻点组成的邻域，近邻值k2一般满足大于低维空间维数d，小于样本的个数Ni（i=1，2，…，C），即d＜k2＜Ni［10］，本 研 究 取k2=9。

为了避免小样本问题，同时寻找一个类间散度矩阵最大和类内散度矩阵最小的低维投影子空间，建立一个基于散度矩阵迹差的函数模型

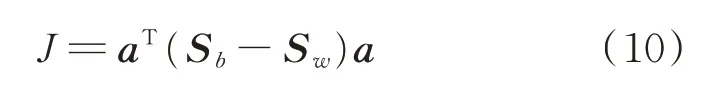
为了调节不同散度的贡献，将式（10）改写为线性组合形式

其中：α为调节参数，0≤α≤1。

为了降低投影后特征分量之间的信息冗余，保留原始故障特征集的几何结构信息，加入正交化约束［1］。建立的目标函数模型为

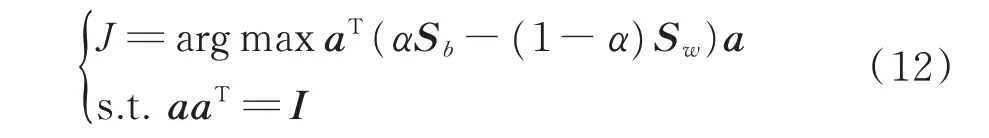
采用拉格朗日数乘法求解式（12），将其解转化为

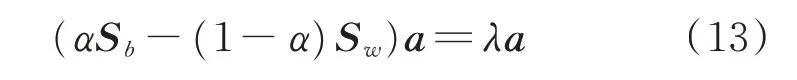
按照特征值由大到小的顺序排列，有λ1≥λ2≥…≥λd，取前d个特征值所对应的正交性特征矢量组成线性投影矩阵A=［a1，a2，…，ad］。

1.2.3 LMDP 算法步骤

LMDP 算法步骤如下：

1）根据式（7），式（9）分别计算类间、类内相似度矩阵B与Wc；

3）建立式（12）所示的目标函数，对其进行特征值分解；

4）按照特征值由大到小的顺序λ1≥λ2≥…≥λd，取前d个特征值所对应的特征向量组成线性投影矩阵A=［a1，a2，…，ad］，并将高维样本集X通过映射矩阵A投影到低维子空间上，得到映射后的低维特征子集Y=ATX。

1.3 基于LMDP 的机械故障诊断

图1 为基于LMDP 的故障诊断流程图，具体实现步骤如下。

图1 故障诊断流程图Fig.1 Procedure of fault diagnosis

输入：高维数据X=｛x1，x2，…，xn｝，LMDP 算法近邻值k1，k2，目标维数d以及调节参数α。

输出：低维敏感特征子集Y和投影矩阵A。

1）提取振动信号的11 个时域特征参数（P1～P11）和13 个频域特征参数（P12～P24），组合得到高维原始故障特征集［11］，统计特征参数如表1 所示。

表1 统计特征参数Tab.1 Statistical characteristic parameters.

2）对高维故障特征集归一化处理后分为训练集X1和测试集X2两部分，将X1输入LMDP 算法中进行训练，得到线性映射矩阵A。用A对X1，X2特征投影得到低维敏感特征子集Y1，Y2。

3）将Y1，Y2分别输入到KNN 分类器中进行故障分类。

2 实验验证及结果分析

2.1 转子故障模拟实验Ⅰ

为了研究LMDP 的可行性和有效性，笔者用图2所示的HZXT-DS-001 型转子振动实验台进行模拟分析。该实验台上4 个加速度传感器分别采集每个轴承座的2 个径向（x，y）和一个轴向方向（z）的振动信号；第5，6 个为电涡流传感器，采集轴的径向振动信号。在转速为2600 r/min，采样频率为20 kHz 的状态下，模拟6 种质量不平衡转动实验，分别记为不平衡1、不平衡2、不平衡3、不平衡4、不平衡5 和不平衡6。转子系统故障状态如表2 所示。采集每种故障的数据样本80 组，前30 组作为训练样本，后50组作为测试样本。对每个通道传感器采集的振动信号分别提取24 个特征参数，14 个通道共得到14×24=336 个特征。

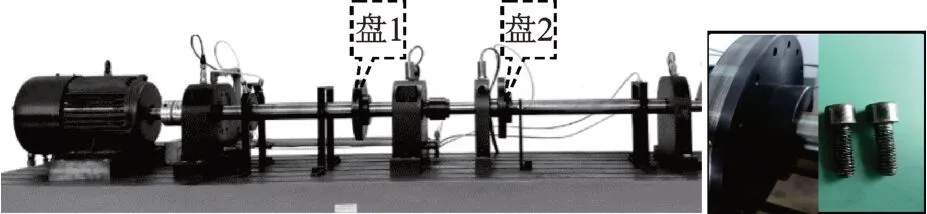
图2 转子振动实验台Fig.2 Experiment of rotor vibration

表2 转子系统的故障状态Tab.2 Fault conditions of rotor system

2.1.1 参数设定情况

笔者需要设定的参数包括LMDP 算法中的近邻值k1和k2，低维空间维数d以及调节参数α。这里，k1=2，k2=9；通常将目标维数d设为样本类别数减1［10］，即d=6−1=5。为了测试调节参数α对故障识别精度的影响，设定间隔为0.1，α为0～1。图3为不同调节参数α的故障识别率。可见，随着α的增大，识别率先增大后减小，在本研究中取α=0.1。

图3 不同调节参数α 的故障识别率Fig.3 Fault identification rate of different adjustment parameters α

2.1.2 高维数据低维可视化

为了验证LMDP 的有效性与可行性，选择与主成分分析（principal component analysis，简称PCA），LPP，LDA 等维数约简方法进行比较。基于上述方法的测试样本三维特征分布结果如图4 所示。可见：PCA 的降维效果最差，同类特征分散，数据的隶属关系非常模糊；LMDP 的降维效果最好，不同故障特征之间完全分离，各类数据清晰可见，相同类型聚集成团；LPP，LDA 两种降维方法的不同类型特征之间都存在一定的混叠，无法完全区分。

图4 基于不同方法的测试样本三维特征分布结果Fig.43-dimensional features scatter distribution of testing samples based on different dimensionality reduction methods

为了进一步说明本研究方法具有较好的降维效果，考察降维后的特征集的可分性，引入了类间、类内距离的可分性指标对测试样本集的分类与聚类程度给予量化评价［12］。低维测试集的C类样本数据为yri（r=1，2，…，C；i=1，2，…，N），其聚类中心为低维特征集的类间距、类内距和可分性指标分别定义为

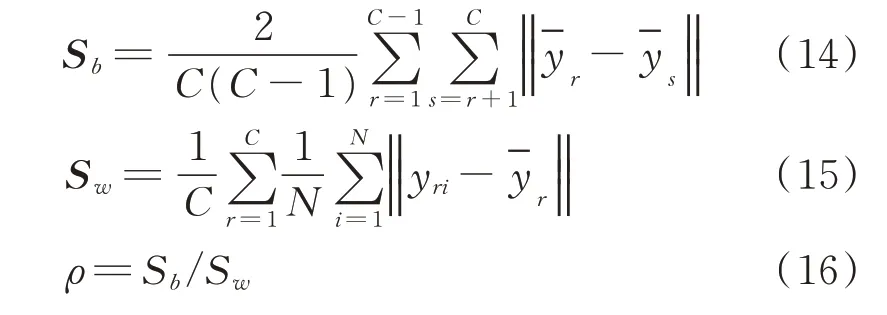
可见，类间距Sb反映了各类别之间的分离程度，类内距Sw体现了每类样本分布的紧凑程度。低维测试集的类间距越大，类内距越小，则可分性指标ρ就越大，特征集的分类聚类效果就越好。

各类算法降维后的可分性指标如表3 所示。可以看出，LPP 的可分性指标最小，只有8.4966；LMDP 的可分性指标最大，高达347.4101。可见，相对于其他算法，LMDP 具有较好的降维效果和较大的可分性，表明LMDP 具有较好的维数约简能力，在数据降维中有一定的优势。

表3 各类算法降维后的可分性指标Tab.3 The separability index based on different dimensionality reduction algorithms

2.1.3 故障分类效果

为了直观反映LMDP 等方法的降维效果，将各个算法降维后的特征子集输入到KNN 分类器中进行故障模式辨识。不同维数约简算法的识别准确率如表4 所示。

从表3 和表4 可知：PCA 的平均识别准确率最低，这是因为PCA 是无监督全局保持算法，在属性约简过程中忽略了样本类别信息，同时很难挖掘出数据的低维流行特征；LPP 的平均识别率略高于PCA，因为LPP 是无监督局部保持算法，没有利用类别信息，导致故障特征解耦不完全、各个特征之间仍存在混叠；LDA 的平均识别率高于PCA 和LPP，是因为LDA 利用了有利于分类的类别标签信息，充分考虑了样本的分散性和内聚性；LMDP的识别准确率最高，主要是因为LMDP 将样本的局部几何信息有效融入到维数约简中，实现了类别信息与数据集局部几何信息的有效结合，在挖掘原始故障数据集中蕴含的转子故障信息的同时，实现对不同转子故障的有效解耦，得到了最有辨别力的低维特征子集，一定程度上提高了故障特征集的可分性。

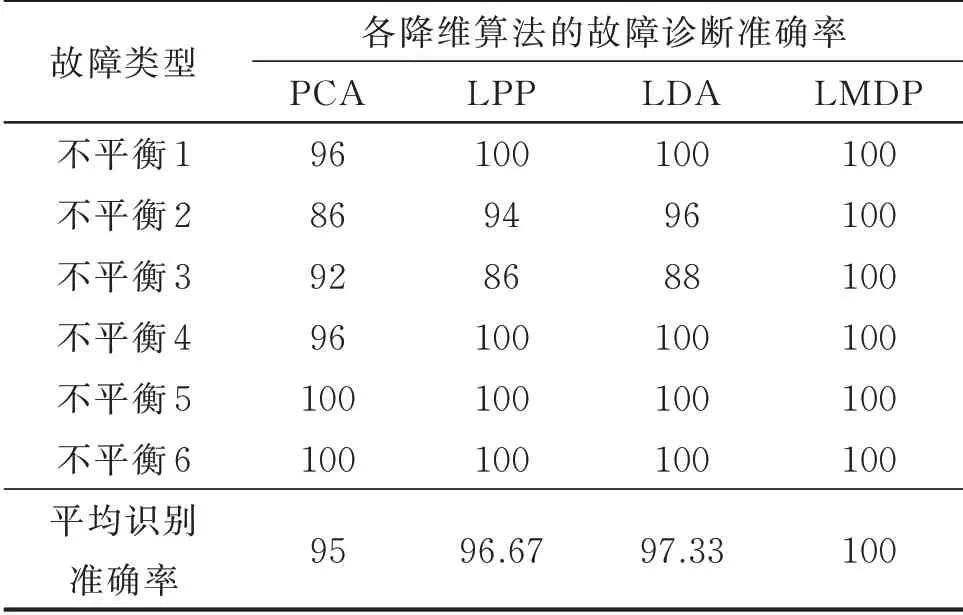
表4 不同维数约简算法的识别准确率Tab.4 The recognition accuracy of different dimensionality reduction algorithms %

为了验证LMDP 算法的泛化能力，将上述4 种算法在不同转速下降维得到的低维特征子集输入KNN 分类器中进行故障模式识别，不同算法在不同转速下的识别精度如图5 所示。可以看出，在不同转速下，LMDP 降维方法的平均识别率明显优于其他3 种降维方法，表明LMDP 具有广泛的适用性和较强的故障识别精度。

图5 不同算法在不同转速下的识别精度Fig.5 Identification accuracy of different algorithms at different speeds

2.1.4 算法复杂度分析

一般降维算法的复杂度O主要由样本个数M、原始维数Q、目标维数d以及近邻值k等因素决定［13］。所提出算法中的复杂度由3 部分组成，建立近邻图需要O（QMlogM），计算邻接权矩阵需要O（M2），对M×M矩阵进行特征分析，所需要的时间复杂度为O（pM2）（p为稀疏矩阵中非零元素与零元素比率）。4 种算法的时间复杂度如表5 所示。可见，由于LMDP 算法需要对局部特征进行提取，局部特征提取时同时考虑到邻域样本的相似性和邻域类别的差异性，计算量有所增加，但相差甚微，相对于提高识别精度，此计算代价是可接受的。

表5 算法的时间复杂度Tab.5 Time complexity of all the algorithms

2.2 转子故障模拟实验Ⅱ

本次实验研究对象为文献［14］中的一套双跨子转子实验台。该实验台上12 个电涡流传感器布置在6 个关键面处相互垂直的方位上，通过不同方位来采集转子系统的振动信号。在转速为2800 r/min，采样频率为5 kHz 的状态下模拟5 种典型转动状态实验，即转子不对中、质量不平衡、动静碰磨、轴承松动和正常状态。采集每种状态的数据样本80 组，其中30 组作为训练样本，剩余50 组作为测试样本。对每个通道的传感器采集的振动信号分别提取时域和频域共24 个统计特征参数，12 个通道共得到288 个特征参数。

2.2.1 高维数据低维可视化

本实验LMDP 所选近邻参数与实验1 相同，k1=2，k2=9，目标维数d=4，α=0.1。为进一步验证LMDP 的可行性与有效性，将原始高维故障数据集经PCA，LPP，LDA 和LMDP 降维，基于不同状态的测试样本三维特征分布结果如图6 所示。由图6可知：PCA 的聚类分类效果最差，各类特征比较分散；LPP，LDA 均存在一定的特征混叠；LMDP 的聚类分类效果最好，同类故障特征比较集中，不同故障特征完全分离。

为了进一步说明LMDP 的优势，按式（16）计算各降维算法降维后的特征集可分性指标，如表6 所示。可见，LMDP 的可分性指标远大于其他算法，进一步证明了LMDP 具有较好的降维效果。

2.2.2 故障分类效果

将低维特征子集用KNN 分类算法进行故障分类，上述4 种降维算法的识别准确率如表7 所示。由表7 可以看出，LMDP 的识别准确率高于其他3 种降维算法，表明LMDP 降维方法较其他方法有较好的维数约简能力，更有利于故障类别的划分。

图6 基于不同状态的测试样本三维特征分布结果Fig.63-dimensional features scatter distribution of testing samples based on different dimensionality reduction methods

表6 各类算法降维后的特征集可分性指标Tab.6 The separability index based on different dimensionality reduction algorithms

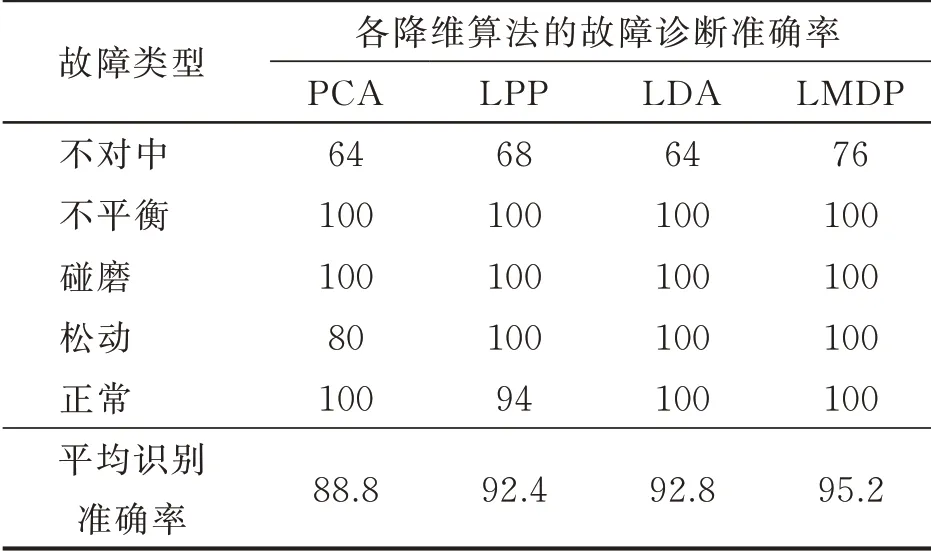
表7 不同降维算法的识别准确率Tab.7 The recognition accuracy of different dimensionality reduction algorithms %

3 结束语

针对转子故障特征集维数过高而导致的分类困难问题，笔者提出了一种基于局部边缘判别投影（LMDP）的故障数据集维数约简方法。首先，将转子振动信号转化为高维特征集；其次，采用提出的LMDP 从高维故障特征集中挖掘出最具有判别能力的低维敏感故障特征子集；最后，通过KNN 对低维敏感特征子集进行故障模式辨识。2 个转子实验结果表明：LMDP 相对于PCA，LPP 和LDA 等维数约简方法，可以提取出可分性更好的低维空间故障特征子集，在模式识别方面具有一定的优势，有效提高了转子故障诊断的精度，为旋转机械智能故障诊断提供了一种新的解决方案。