浮筏隔振系统拓扑优化研究与振动特性分析∗

崔洪宇， 朱海涛，2

（1.大连理工大学船舶工程学院 大连，116024） （2.中车青岛四方车辆研究所有限公司 青岛，266031）

引 言

随着现代舰船对隐身性和舒适性等需求的不断提高，基于浮筏隔振系统较好的隔振性能和系统稳定性，浮筏系统被越来越广泛地应用于舰船设备的隔振中［1-3］。由于舰船上空间限制和重量的严格要求，浮筏隔振系统面临着过多占用总体重量和空间的问题。因此，进一步提高浮筏系统的隔振性能，改善浮筏隔振装置的重量和空间尺寸，对浮筏隔振系统的优化设计具有重要意义。文献［4-5］对影响浮筏隔振性能的因素进行了研究。文献［6-7］将筏架的质量分布和尺寸参数作为优化设计的变量，对筏架结构形式进行了减重优化设计。文献［8-9］对浮筏隔振系统的隔振器数量、布置方式和刚度阻尼参数进行了优化设计，以改善浮筏系统的隔振性能。针对浮筏隔振系统，评定其隔振性能的指标主要有传递功率流、振级落差和力传递率等［10-13］。Goyder等［14］将传递功率流作为优化设计的评判标准，从理论分析和仿真实验2 个角度对浮筏结构的减振性能进行了研究。黎上达等［15］建立了浮筏筏架的参数化有限元模型，以振级落差作为隔振效果的评价指标，研究了筏架几何参数对浮筏系统隔振性能的影响。

笔者基于Optistruct 软件，采用变密度方法对浮筏隔振系统进行了减重拓扑优化设计。基于ANSYS 软件，采用有限元分析方法建立浮筏隔振系统模型，对其振动传递特性进行研究。选用空气弹簧作为隔振器，搭建了浮筏隔振实验系统，采用振级落差作为评价指标，研究了实际浮筏模型中的振动传递特性。

1 浮筏隔振系统的拓扑优化分析

结构拓扑优化技术中的变密度法是一种高效的结构优化方法，优化过程中假定材料密度可变，设计变量即为定义的材料密度，通过迭代计算得到优化结构中材料的最优分布形式。针对浮筏隔振系统的优化问题，建立数学模型为

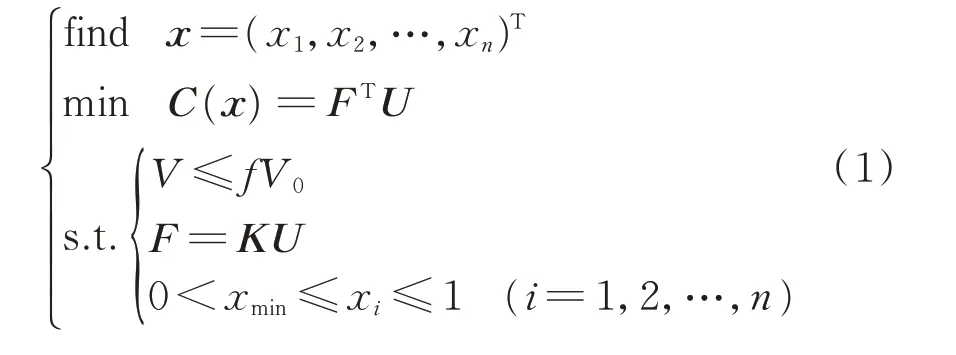
其中：n为设计变量个数；C(x) 为目标变量；F为作用在浮筏结构上的外载荷向量；U为浮筏结构的位移向量；V为浮筏结构优化后的体积；V0为浮筏结构的初始体积；f为浮筏结构的体积约束参数；fV0为优化后浮筏结构体积的上限值；K为浮筏结构的总刚度矩阵；xi∈[xmin，1]为设计变量，即筏架结构的密度参数，为了避免优化过程中总刚度矩阵奇异，取xmin=0.001。

笔者采用变密度法中的固体各向同性材料惩罚模型（solid isotropic material with penalization，简称SIMP），引入惩罚因子，避免在结构拓扑优化的过程中出现中间密度单元，其数学模型为

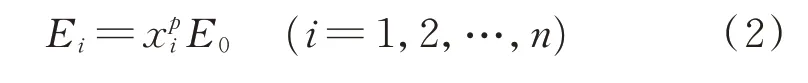
其中：Ei为单元i的弹性模量；p为惩罚因子；E0为单元xi=1 部分的弹性模量。

笔者采用优化准则算法求解建立的数学模型。基于SIMP 的拓扑优化模型为

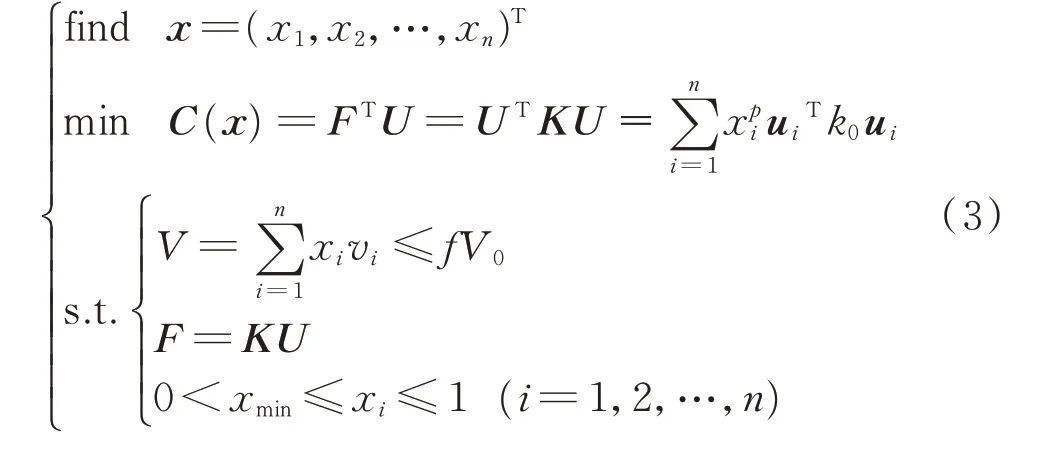
数学模型的拉格朗日函数表达式利用结构刚度矩阵的对称性，经过化简可得

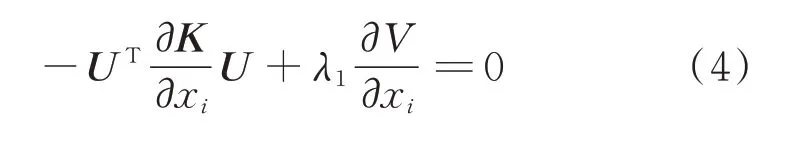
其中：λ1为拉格朗日乘子。

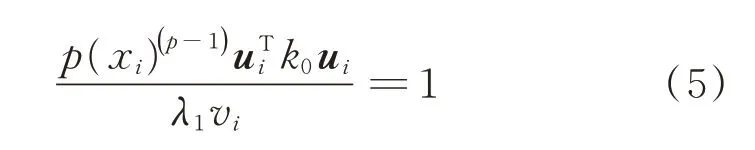
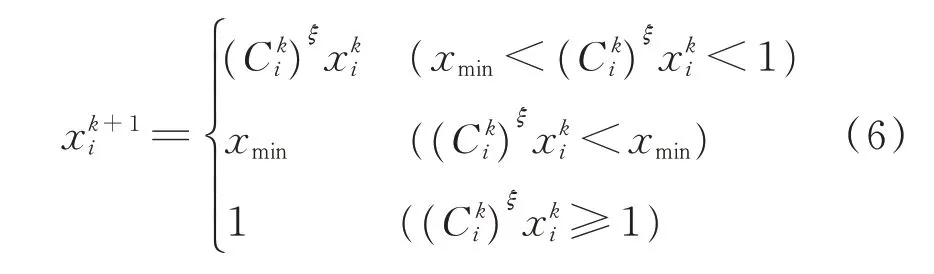
其中：ξ为阻尼系数，可使拓扑优化计算过程保证收敛。

对设计变量不断进行迭代更新，直至计算结果收敛，针对误差ε，即

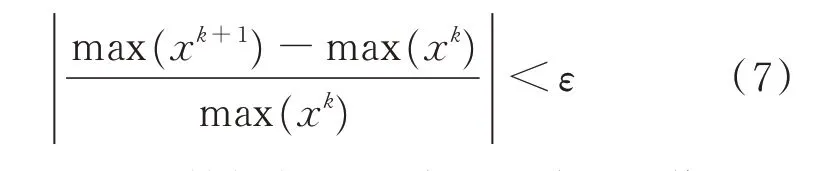
输出得到整个结构优化设计的设计变量值和最佳的筏架结构拓扑优化形式。

由于很难确定初始筏架结构形式，所以采用0.8 m×0.4 m×0.1 m 的立方体结构作为初始筏架，结构材料为Q235 钢，筏架的上下表面设置硬点作为隔振器连接点，优化空间采用solid 单元进行离散，得到筏架结构的有限元模型如图1 所示。

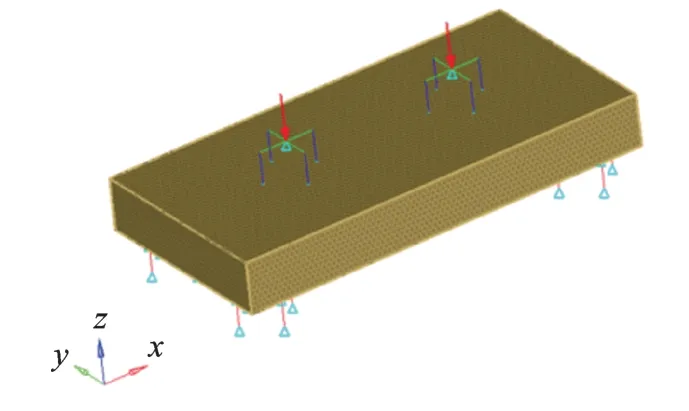
图1 筏架结构的有限元模型Fig.1 Finite element model of raft structure

浮筏隔振系统中的机械设备为振动电机，采用CONM2单元进行模拟，振动电机与上层隔振器上端多点约束。隔振器采用空气弹簧，用CELAS1单元进行模拟，每个空气弹簧采用4 个弹簧单元并联的建模方式。空气弹簧的刚度与其承受的载荷有关，经过计算，每个空气弹簧的刚度为70 N/mm。振动电机的最大激励力为920 N，由于激励力频率与筏架固有频率相差较大，为了简化计算，故仿真时将激励力设为静态力均匀分配到2 个CONM2单元上。

在考虑整个浮筏系统隔振性能和筏架刚度的情况下，设定约束条件为上下层隔振器与中间筏架连接点处的位移，设定优化目标为筏架的质量最小。通过迭代计算得到拓扑优化后整个筏架结构的材料密度分布云图如图2 所示，中间红色部分材料密度趋于1，四边深蓝色部分材料密度趋于0。

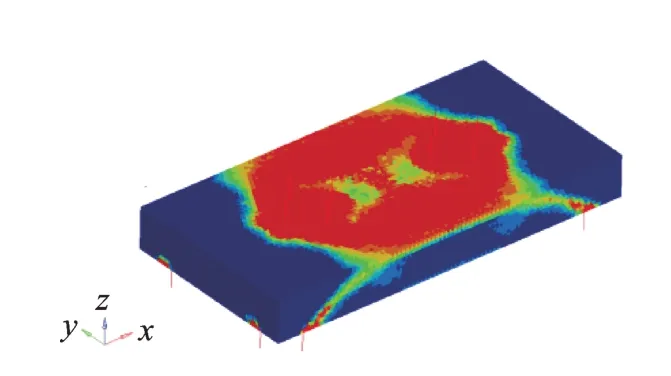
图2 拓扑优化后的材料密度分布云图Fig.2 Topologically optimized material density distribution cloud map

图3 材料密度分布云图（密度阈值为0.6）Fig.3 Material density distribution cloud map (density threshold is 0.6)

图3 为单元密度阈值为0.6 时的材料密度分布云图，即材料密度大于0.6。从图2，3 可以看出，上下层隔振器与筏架连接点处的材料比较集中，筏架中心处以及靠近筏架边缘的位置，材料分布较少。因此，在进行筏架结构优化设计时，可以将中间和两端设计为空心结构。

拓扑优化迭代计算得到的是一种理想的材料密度分布形式，很难直接应用于实际工程结构。运用OSSmooth 工具对筏架结构进行规则化处理，保留作用较大的材料，并考虑筏架的强度和刚度，得到规则化处理后的优化筏架如图4 所示。

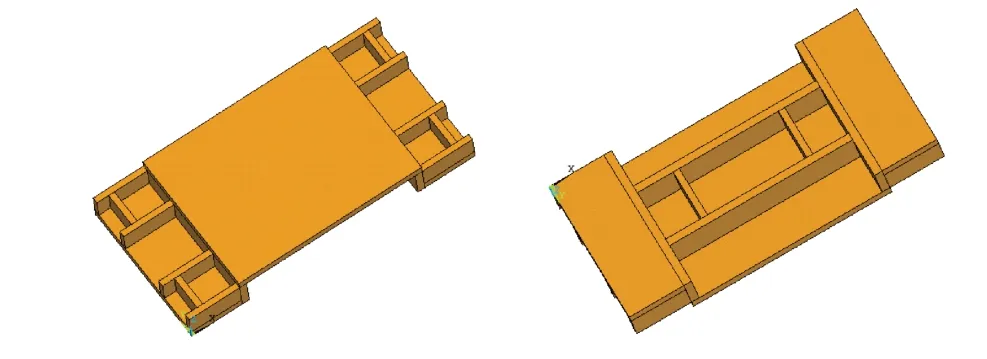
图4 规则化处理后的优化筏架Fig.4 Optimized raft after regular treatment

2 优化筏架的有限元分析

在整个浮筏隔振系统中，中间筏架的动力性能与系统整体动力性能有很强的相关性。因此，对中间筏架进行有限元分析十分必要。根据得到的优化筏架建立有限元模型，对其进行自由边界条件下的模态分析，计算得到优化筏架的前2 阶固有频率分别为228 Hz 和594 Hz，其振型如图5 所示。优化筏架的固有频率远大于激励频率，有效避免了共振的产生。

图5 优化筏架的前2 阶振型Fig.5 The first two modes of vibration of optimized raft

基于ANSYS 软件，采用有限元分析方法建立初始筏架与优化筏架模型，使用COMBIN14单元对隔振器进行模拟，隔振器与浮筏筏架通过共享节点的方式连接。对其进行静力分析，得到优化前后筏架的最大应力值分别为2.16 MPa 和0.64 MPa，优化前后筏架应力分布如图6 所示。优化后筏架最大应力小于初始筏架，且远小于材料的屈服应力，说明优化后筏架更不容易达到应力极限。

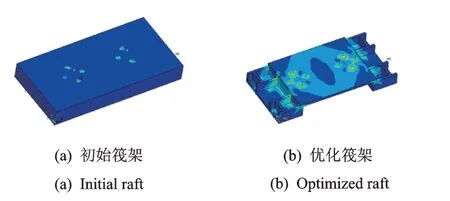
图6 优化前后筏架应力分布图Fig.6 Stress distribution of raft before and after optimization

3 浮筏隔振系统的功率流有限元分析

笔者采用振动功率流的方法研究振动能量在浮筏隔振系统中传递的特性。将力和位移写为

其中：T=为振动频率；̇为速度；和均为复数。

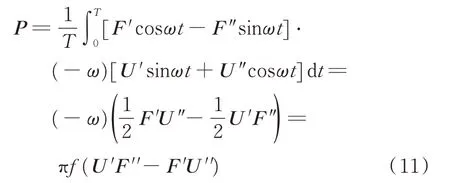
建立如图7 所示的浮筏隔振系统有限元模型。在机械设备上施加垂直方向的集中力，下层基础的底端施加全约束。对整个浮筏隔振系统进行谐响应分析，获取其在给定激励下的动态响应数据，从而得到各分析节点的传递功率流。

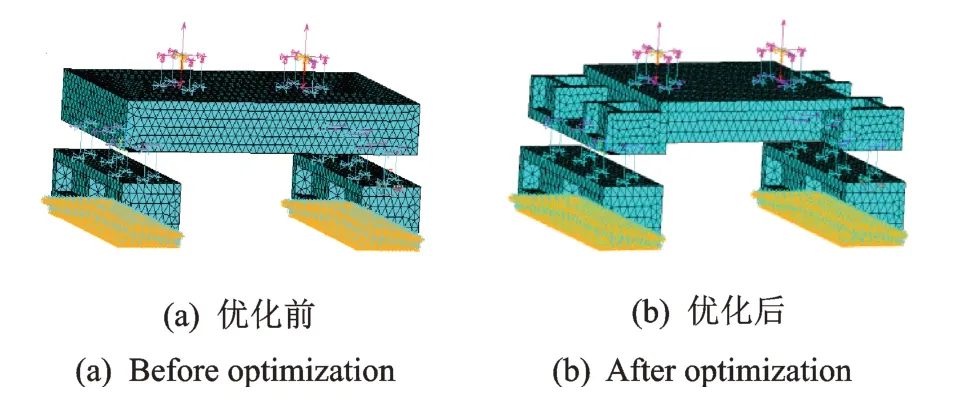
图7 浮筏隔振系统有限元模型Fig.7 Finite element model of floating raft vibration isolation system

在实际工程应用中，垂直方向的振动是浮筏隔振系统中振动的最主要形式，也是绝大部分能量的传递途径，故笔者仅考虑了垂直激励作用下浮筏系统中的功率流传递特性。图8，9 分别为仿真分析得到的优化前后浮筏隔振系统功率流传递曲线。

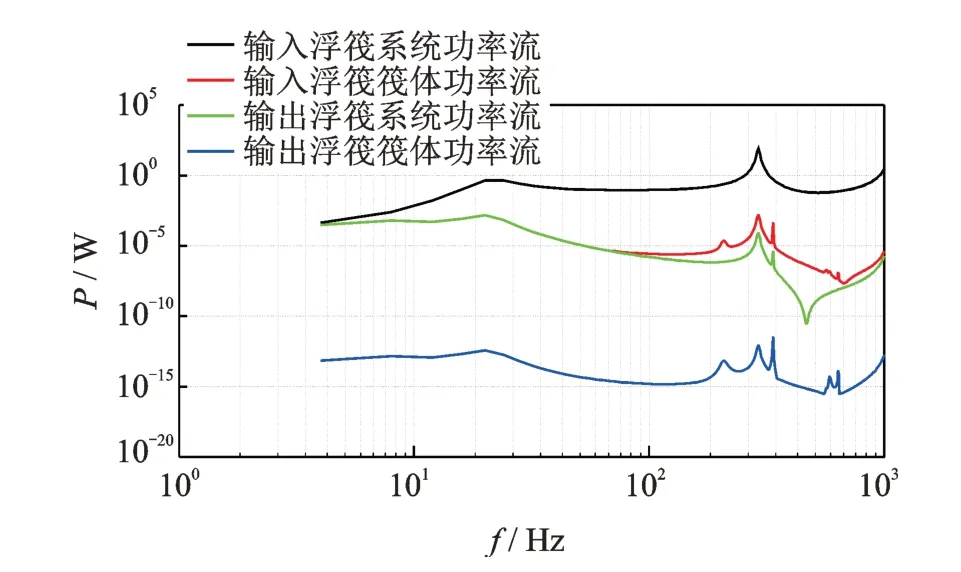
图8 优化前浮筏隔振系统功率流传递曲线Fig.8 Power flow transfer curve of floating raft isolation system before optimization

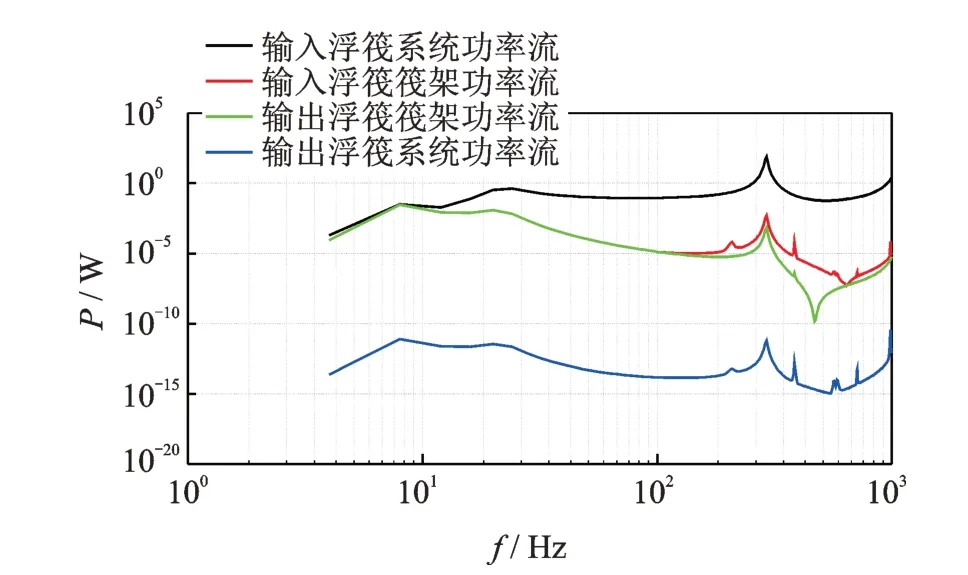
图9 优化后浮筏隔振系统功率流传递曲线Fig.9 Power flow transfer curve of floating raft isolation system after optimization

可以看出，优化设计之后，浮筏隔振系统的筏架质量减少了约60%，但仍具有较好的隔振性能。优化前后浮筏隔振系统的隔振效果基本不变，但筏架质量却大大减小，说明笔者较好地优化了筏架结构。

4 浮筏隔振系统实验

基于拓扑优化的结果，对优化筏架进行设计加工，加工过程中需在筏架上开设自锁接头孔洞和螺栓孔洞，以利于后期的实验搭建。优化筏架的详细设计如图10 所示。

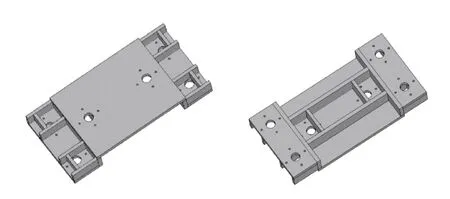
图10 优化筏架的详细设计图Fig.10 Detailed design of optimized raft frame

优化筏架加工完成之后，将振动电机、上层机座、中间筏架、下层基础和空气弹簧等进行组装连接，搭建整个浮筏隔振系统，并将其固定在实验台上，如图11 所示。

图11 浮筏隔振系统实验示意图Fig.11 Schematic diagram of floating raft isolation system experiment

笔者采用振动电机，其最大振动力为920 N，刚性安装在电机机座上。采用的空气弹簧为单囊式，充气压力范围为0.2 MPa～0.8 MPa。针对浮筏隔振系统的振动特点，在每层面板的空气弹簧附近布置加速度传感器进行振动测量。笔者共采用5 种实验工况对浮筏隔振系统振动性能进行分析，表1 为浮筏隔振系统实验工况汇总。

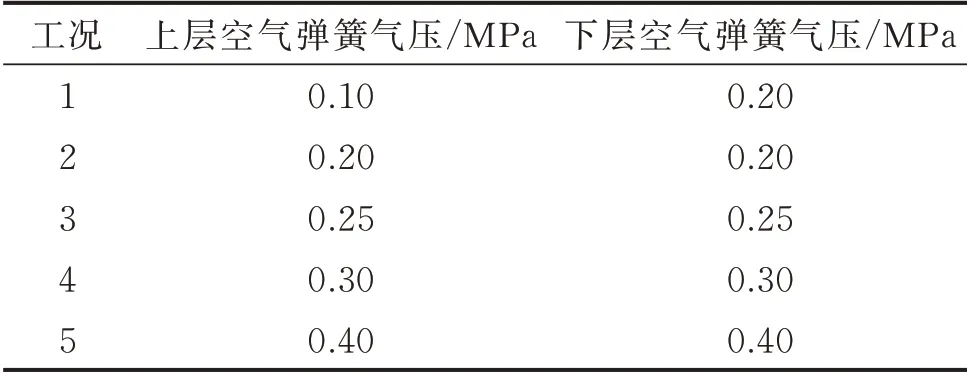
表1 浮筏隔振系统实验工况汇总Tab.1 Table of experimental conditions of floating raft isolation system

采用振级落差作为浮筏系统隔振效果的评价指标

其中：Li为第i个测点的振动加速度级为加速度有效值；a0为加速度基准值，取a0为10−6m/s2。

实验中振动激励频率的变化范围为15～50 Hz，相邻频率间隔为5 Hz。通过测量得到浮筏隔振系统在5 种工况下上层机座、中间筏架和下层基础的加速度振级曲线如图12 所示。

由图12 可以得出如下结论：

1）当上层空气弹簧的气压小于等于0.25 MPa时，中间筏架的加速度振级较小，上层机座与中间筏架之间的加速度振级落差较大；当上层空气弹簧的气压大于0.25 MPa 时，中间筏架的加速度振级明显增大，上层机座与中间筏架之间的加速度振级落差较小。这说明随着气压的增大，空气弹簧具有较大的刚度，振动衰减效果减弱，此时需要上下层空气弹簧共同作用才能将振动减小到较低水平。

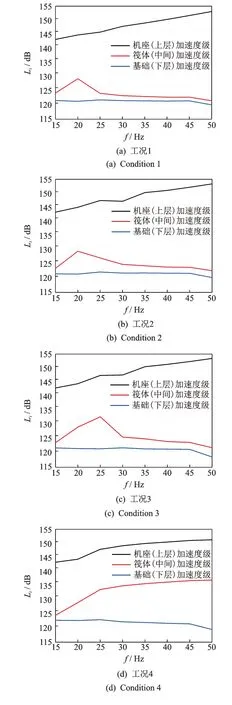
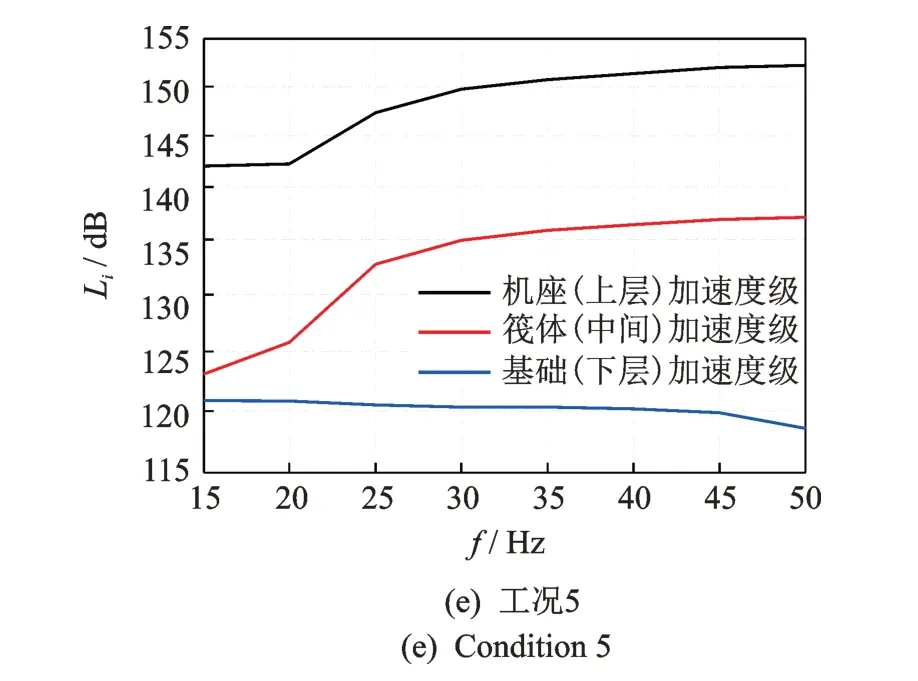
图12 浮筏隔振系统在5 种工况下的加速度振级曲线Fig.12 Acceleration vibration level curve of floating raft isolation system under five working conditions

2）频率越高，上层机座与下层基础之间的加速度振级落差就越大。这说明浮筏隔振系统高频区域的振动衰减效果比低频效果更好，随着激励频率的增高，振动能量衰减的越多。

图13 为有限元仿真和实验结果进行对比的浮筏隔振系统的加速度振级曲线。可以看出：

图13 仿真和实验下浮筏隔振系统的加速度振级曲线Fig.13 Acceleration vibration level curves of floating raft isolation system under simulation and experiment

1）仿真中浮筏隔振系统上层机座和中间筏架的振动加速度级与实验结果相差不大，但均小于实验结果。主要原因是振动电机产生的振动能量比较分散，除了垂直方向的振动，还有其他方向的振动以及扭矩产生的振动，而有限元仿真分析仅考虑了振动电机垂直方向的振动。

2）仿真中浮筏隔振系统下层基础的振动加速度级远小于实验结果。其原因主要是实验中浮筏隔振系统的下层基础与实验台之间通过螺栓连接，由于机械原因和振动的影响会有些许松动，并不是完全紧固，而有限元仿真中基础的下端是各个方向的全约束，下层基础几乎不会振动。

5 结束语

采用变密度法对浮筏隔振系统进行了拓扑优化分析，经过规则化处理，得到了满足约束条件的优化筏架形式。建立优化筏架的有限元模型，对其进行模态分析和静力分析，结果表明，优化筏架的固有频率远大于激励频率，避免了共振的产生，同时最大应力远小于材料的屈服应力，具有较大的强度。建立整个浮筏隔振系统的有限元仿真模型并进行系统的振动功率流传递特性分析，证明优化前后浮筏隔振系统的隔振效果基本不变，但筏架质量却大大减小，较好地优化了筏架结构。基于拓扑优化设计的结果，对优化筏架进行设计加工，采用空气弹簧作为隔振器，搭建整个实验系统，根据测试结果得到浮筏隔振系统各层振动加速度级曲线图。结果表明，空气弹簧的隔振效果与其气压有关，当气压较大，即刚度较大时，空气弹簧的隔振效果明显减弱。笔者对浮筏隔振系统的结构优化方法和振动特性分析方法为实际工程结构的优化设计提供了技术支持。