基于分层平衡抽样的多目标代表性样本设计——以住户调查为例

巩红禹,张士琦,王春枝

(内蒙古财经大学 a.统计与数学学院;b.内蒙古经济数据分析与挖掘重点实验室;c.经济应用统计评价研究中心,内蒙古 呼和浩特 010070)

一、引 言

抽样调查的目的是通过样本数据推断总体总量、总体均值、总体比例等特征。对总体特征的估计效率不仅与样本量多少有关,还取决于样本单元的权数设计及其代表性。样本单元的基础权数是该样本单元一阶包含概率的倒数,其涵义是代表含自身在内的总体单位个数,这是样本代表性的一个充分表现。充分利用总体的辅助信息,对样本施加约束条件,可以显著提高样本的代表性。这里所说的辅助信息是针对调查者所感兴趣的目标变量而言的,在抽样调查开始之前就已经为调查者所知。我们把与目标变量有联系的变量称为辅助变量,可以总结为如下两点:辅助变量必须是与目标变量高度相关的;辅助变量的信息质量较好,能够对目标变量的估计起到积极作用。辅助信息通常来源于近期的普查资料、企事业单位的生产经营和业务记录及各级政府部门的行政记录等。辅助信息可以是定量辅助信息,也可以是定性辅助信息,前者如人口数、年龄、税后收入等等,后者如性别、婚姻状况、居住地区等等。

1934年,波兰统计学家奈曼在英国皇家统计学会上宣读了奠定现代概率抽样方法基础的论文,提出随机抽样的合理性,并且提出了抽样的最优分层方法,这被认为是现代抽样历史的新纪元[1]。分层抽样设计一直是概率抽样研究的重要问题之一。

平衡抽样思想的先驱者是基尼。基尼提出了著名的基尼系数,用以衡量一个国家和地区的收入差距,他本人也因此被后人铭记。在意大利一次调查中,基尼以目的抽样方式,从214个区域中选择了29个区域作为非概率样本,他的目的抽样带有这样的约束,选择了与目标变量相关的几个辅助变量,使得其样本的简单均值等于其总体的简单均值,用以提高总体目标特征估计的准确性[2]。这里的样本事实上是简单平衡样本,但不是随机样本。基尼考虑到了利用辅助信息提高样本代表性,进而提高了总体特征估计准确性的问题。耶茨肯定了Gini平衡抽样思想的合理性,认为随机抽样与平衡抽样并不冲突矛盾,并且提出了一种以“替代”方式获取随机平衡样本的方法[3]。自此之后,众多统计学家在随机抽样的框架下研究平衡样本对总体目标特征估计的有效性,并将简单平衡拓展到一般平衡。平衡样本是指辅助变量总量的加权估计(霍维茨汤普森估计量)等于总量真值。平衡抽样设计是在传统等概抽样或者不等概抽样基础上,借助于与总体目标变量相关的辅助变量,通过对样本施加平衡约束,获得有效降低目标参数估计值离散程度的样本,进而达到降低目标估计方差,提高参数估计效率的目标。

统计学者已对平衡样本进行了卓有成效的研究。一是基于模型视角,平衡样本使得估计量对模型具有稳健性,这是它的一个突出优势。由于总体的真实模型未知,因此研究者利用观测数据统计建模时需要进行模型选择。如果选择模型与总体的真实模型吻合,总体总量或者总体均值的估计是最优线性无偏估计。但是一旦选择模型与总体的真实模型不符,估计量将不满足无偏性和有效性。如果超总体模型是线性模型,平衡样本对总量的最优无偏估计具有稳健性[4-5]。二是平衡样本的获取及应用。获取途径主要有拒绝抽样和立方体法。拒绝抽样(rejective sampling)算法基于初始的抽样设计随机抽样,通过控制平衡变量的估计与总体真值差异的容忍阈值,得到满足平衡约束的样本[6-7]。拒绝抽样方法能够精确满足包含概率,但耗费的时间成本比较高。Tille提出一种获取平衡样本的几何方法立方体法(the cube method)[8]。Chauvet等证明了立方体法获取的平衡样本具有设计无偏性[9]。法国住户调查采用平衡抽样设计获取初级样本单,平衡变量选择了收入和不同的年龄段[10-11]。

国内学者也对样本代表性分别从事前保证和事后评估两个视角进行了讨论。事前保证角度,冯士雍认为利用辅助信息获得好的代表性样本[12]。金勇进结合湖北省工业企业数据就工业企业规模的划分标准讨论规下工业企业抽样的代表性问题[13]。事后评估角度,王萍萍利用第二次农业普查数据和县市统计数据,探索调查县农民收入水平对所在省农民收入水平代表性的评估[14]。宋子轩等结合人口普查数据尝试从样本与总体结构差异角度构建一套指标和假设检验对样本代表性进行事后评估[15]。

分层平衡抽样设计也能实现多目标调查,即利用一套样本追求多个目标特征的总体或者层的信息。多目标调查中,由于总体单位在各个调查目标上可能存在着很大的差异,不同调查目标的分布差异显著,针对某个调查指标设计的抽样调查方案,可能会导致另一指标有较大的抽样误差,因而如何进行抽样设计使之对各个目标的抽样误差较小,是设计多目标调查方案的难点所在。美国农业部专家Bailey和Kott于1997年首先提出多变量PPS抽样(MPPS),并在农业抽样调查中成功应用[16]。金勇进提出使用一套地域样本的MPPS抽样方法同时进行规模以下工业企业和个体工业单位的调查思路,最终得出使用地域抽样进行规模以下工业调查具有可操作性[17]。澳大利亚普查局应用住户调查数据探索了基于平衡样本的多个目标参数的推断效率,结果表明目标估计的方差显著降低[18]。这里提出的分层平衡抽样设计通过选择与目标相关的多个辅助变量,使得样本对于多个目标参数而言,所选择的辅助变量与不同的目标有相关性,都具有良好的代表性,避免了一套样本在推断多个目标参数时顾此失彼的缺点,进而完成总体的多目标有效推断。

本文从抽样设计的事前保证和事后评估两个视角,研究分层平衡抽样的代表性及多目标性问题。分层抽样不仅提高目标特征的估计效率,还能够估计层的目标特征。平衡抽样控制辅助变量的离散程度进而降低目标估计的抽样误差。将分层与平衡抽样结合构成的分层平衡抽样方法不仅实现层内样本单元的平衡,也能实现样本的整体平衡。以住户调查的初级单元抽样框为例,对城镇化率采用累积平方根法进行分层,对分层平衡样本实证表明,对于平衡变量而言,样本与总体结构相近,而且层内样本结构类似于层结构。进一步对总体和层的多个目标特征进行估计,相对误差在合理范围内,说明分层平衡样本对总体或者层有良好的代表性。这为国内政府多目标调查设计代表性样本提供了新的思路,弥补了国内对代表性样本和多指标调查研究的相对不足。

二、分层平衡抽样设计

(1)

假设抽样设计之前抽样框包含辅助变量x=(x1,x2,…,xq)。如果抽样设计ph关于辅助变量x=(x1,x2,…,xq)满足第h层辅助变量的估计等于该层的总量,即:

(2)

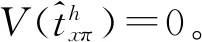
固定规模的分层抽样本身是平衡抽样的特殊情形。事实上,平衡变量只取包含概率x=π,那么由平衡方程(2)有:

即各层单元包含概率的和等于该层的样本量。实施平衡抽样设计时,选择平衡变量xk1=δk1,δk2,…,xkH=δkH,其中δkH=1,如果k∈UH,否则δkH=0。

通常来说,使样本精确地满足平衡方程是不可行的。假定第h层包含100个单元,其辅助变量x有两个值0和1,其中有53个单元的辅助变量取值为0,47个单元的辅助变量取值为1。等概率选择样本量为10的样本,那么由平衡方程有:

但是显然有:

平衡抽样设计可以通过立方体方法实现。立方体法以几何表现形式获取平衡样本,已经被嵌入权威的统计软件SAS、强大的矩阵计算软件Matlab、研究的开放软件R中,实践中具有很强的操作性。立方体法能够获取相等包含概率与不等包含概率的平衡样本,这里简要阐述立方体法的思想。在N维实数空间RN中,2N个样本对应于2N个向量。每个向量是N维立方体的顶点,样本的个数是N维立方体顶点的个数。S={S1,S2,…,SN},如果第k个单元入样,Sk=1,否则为0。样本S可以视为N维立方体的一个顶点。平衡方程通过N维实数空间的N-P维子空间表示,其中P为平衡变量个数。选择平衡样本即是寻找N维立方体与其约束N-P维子空间的交集。

立方体法可分为两个阶段,包括腾飞阶段与着陆阶段。腾飞阶段是以包含概率为起点的随机游走过程,随机选择K={[0,1]N∩Q}的顶点,当N维立方体与Q相交时停止。如果腾飞阶段结束时,仍然无法获得精确满足平衡方程的样本,此时需要实施第二阶段——着陆阶段。着陆阶段选择一个近似满足平衡条件的样本,使得E(S|π*)=π*,其中π*是腾飞阶段结束时总体单元的包含概率,通过下面的线性规划来实现:

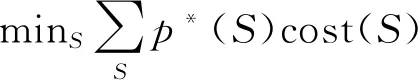
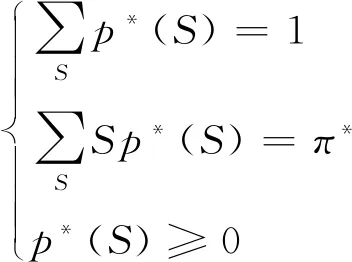
其中cost(s)是惩罚距离函数。

E(h*)=πh

(3)

(4)

(5)

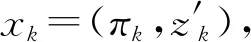
第一步实施腾飞阶段尽力确保层内样本对层保持平衡,当第一步结束时,式(4)变形为∀h=1,2,…,H,有下式:

(6)

对所有层加和,进一步有:

(7)

第二步实施腾飞阶段努力使得样本在总体内保持平衡,这一步结束时,式(4)变形为:

(8)

结合(7)、(8)两个表达式,有下式:

(9)

第三步放松平衡约束,通过线性规划完成平衡抽样过程。

π估计量的方差公式(1)与二阶包含概率πkl有关,但πkl的计算很复杂,对于平衡抽样设计,π估计量的方差和方差估计公式可以由下面的式(10)和(11)给出:

(10)

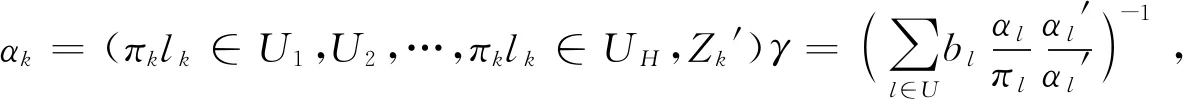
(11)

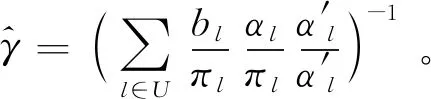
三、实证分析

(一)样本的事前设计

分层平衡抽样已用于1999年法国的INSEE调查初级单元的选择。主样本来自于住户调查,其抽样框来自1999年的人口普查。首先将住宅分为城市单位和农村单位。对于居民规模小于100 000的城市,从中选择大约为6%的居民作为样本进行调查。调查将行政区域分为8层,选择了四个辅助变量即税后净收入、三个年龄组,每个层采用平衡抽样设计。样本确保在每个层内关于辅助变量平衡,同时也满足样本关于辅助变量的整体平衡。

里选择城镇住户调查具有一定的典型性和代表性。以初级抽样单元县级行政单位为例进行说明。城镇住户调查的目标是了解人均可支配收入、劳动力从业状况、居民消费支出等住户的基本情况,服务于国家宏观经济管理,包括用于监测贫困人口、国民经济核算、CPI权数设计等。2010年第六次人口普查中的分县人口普查资料提供了分县的不同年龄阶段、性别等人口数量信息,这为平衡变量的选择提供了可行性。

城镇化作为社会经济发展的必然选择,在人口转移、产业调整、工业发展、科技进步、文化交流等方面发挥重要作用,是衡量区域经济社会发展水平的重要指标。城镇化水平采用通用的测度指标即县级单位的城镇人口除以县级单位的总人口。根据城镇化水平,采用累积平方根方法,对内蒙古80个旗县市进行分层,共分为4层。过程如下:根据城镇化率对旗县进行自然分组,然后给出频数分布表(表1),计算频数的平方根、累积平方根,确定分层间隔,找出分层界点,分别为8,16,24。分层结果见表2。

表1 城镇化分组

表2 累积平方根分层

住户调查中农村层的调查假定初级单元的样本量为3个,各层根据人口规模按比例分配样本量,分配结果如表3。各层分配的样本量分别为10,7,5,8。

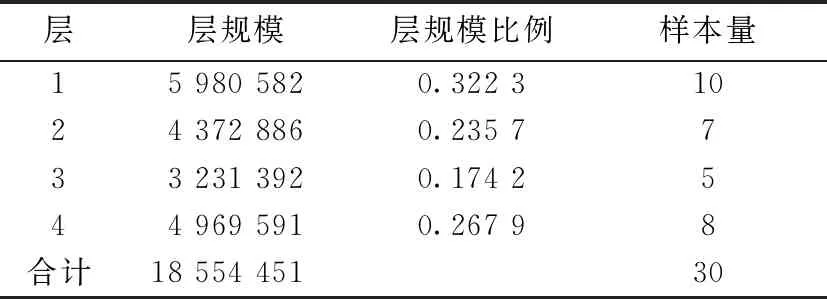
表3 样本量的比例分配

R语言中包Balanced Sampling中命令Cube Stratified或者包Sampling中命令balancedstratification实现分层平衡抽样。假设文件名data,户籍人口数量与一阶包含概率(pik)成正比,平衡变量选择了性别男(nan)、性别女(nv)、0～14岁(X014)、15～24岁(X1524)、25～44岁(X2544)、45～59岁(X4559)、60岁以上(X60ys)人口数,ceng为分层变量,关键代码如下:

Library(Sampling);#载入Sampling包

X=cbind(data＄nan,data＄nv,data＄hs,data＄X14,data＄X1524,data＄X2544,data＄X4559,data＄X60ys)#平衡变量

s=balancedstratification(X,data＄ceng,pik,comment=TRUE)# 获得平衡样本

fcs<-getdata(data,s)#获取文件数据

抽得样本结果如表4,抽样结果满足各层事先设定的样本量要求。

表4 分层平衡抽样结果

如表5所示,根据分层平衡抽样设计的原理,各层满足层平衡方程(2),也满足样本关于总体的平衡。从表5看出,平衡变量的π估计第二层男性估计的相对误差最高为4.60%,第三层45～59岁人口数量估计的相对误差最高为7.01%,处于合理的接受范围,其他各层平衡变量估计的相对误差都很小。

表5 各层样本与层、样本与总体关于平衡变量的π估计及相对误差

(二)分层平衡样本的事后评估

平衡样本获得之后,我们进行样本代表性的事后评估。事后评估从样本关于平衡变量的结构与总体的差异,目标参数估计的相对误差进行代表性评估。

选择结构代表性检验的差异率为:

比较样本总体属性水平之间的差异程度。其中p表示样本结构,P表示总体结构。

表6反映了样本结构与总体结构的差异,第二层60岁样本以上人口与总体结构的相对误差为7.51%,在合理的误差范围内,其他各层在平衡变量上样本与总体的结构相对误差都很小,这在一定程度上说明分层平衡样本对层有代表性,对总体也有代表性。

表6 各层样本与层、样本与总体关于平衡变量的结构差异

我们选择人口教育年限、男性教育年限、女性教育年限、城镇人均可支配收入和农牧民人均纯收入作为各层的目标特征或者总体特征。这些指标与年龄结构和性别结构密切相关。比较样本和总体的加权算术平均数与总体平均数的差异,以此进一步说明平衡设计的有效性,同时也说明平衡样本能够实现多目标调查。总体平均数通过下面的公式计算:

样本加权算术平均数可以作为总体平均数的估计,其计算公式为:

表7 层及总体的目标参数估计

第一层和第二层的农牧民人均纯收入相对误差分别为9.64%和9.13%,在合理的接受范围内,其他目标参数的估计相对误差很小,说明分层平衡抽样设计是有效的。

四、结 论

政府调查中,样本的代表性直接关乎政府的数据质量。平衡抽样设计并未使样本失去随机性,正如分层抽样不会使得样本失去随机性。平衡变量的选择不宜过多,根据Tille建议,40个以内为最佳。分层平衡抽样不仅实现样本的全局平衡,也能实现层内的局部平衡。本文提出的池着陆分层抽样算法能够实现这个目标。这里对住户调查的初级单元进行分层平衡抽样设计探索性研究,具有一定的代表性。分析结果表明,根据城镇化率进行分层,具有一定的合理性。将分层与平衡抽样结合构成的分层平衡样本具有层内样本结构关于平衡变量与层结构接近,样本与总体关于平衡变量相似的特点。本文提到的平衡抽样在抽样之前就把与不同总体目标相关的平衡变量作为选择,使得一套样本同时满足多个调查指标的要求,能够有效解决多目标推断的问题。通过估计与性别、年龄变量相关的人口教育年限、男性教育年限、女性教育年限、城镇人均可支配收入、农牧民人均纯收入等多个重要社会经济指标,说明了分层平衡设计的有效性,也说明了平衡抽样设计能够解决抽样调查中多指标调查问题,提高了样本的使用效率,为政府统计抽样调查提供了新的思路和途径。

对样本设置约束是使样本满足一定的条件,也意味着样本对总体的信息反映更多。样本规模固定和分层本身都是对样本设置约束。这里通过对样本进一步设置平衡约束,样本某些特征的估计量和这些特征的已知总量一致,这样能减少目标估计量的离散程度,即达到减少方差,提高参数推断效率的目标。

对样本施加约束似乎与随机化矛盾,因为它限制了具有非零概率的样本数量。然而,样本的可能数量非常巨大,以至于即使有几个约束,具有非零概率的可能样本数量仍然很大,假设估计值服从正态分布仍然是合理的,从而给出参数的区间估计。平衡抽样避免抽取到糟糕的样本,这些样本关于辅助变量的估计与总体的真值相差甚远。