变分模态分解模型中关键参数K的辨识研究——基于加权最大信息系数法

夏茂森,江玲玲

(安徽财经大学 a.统计与应用数学学院;b.会计学院,安徽 蚌埠 233030)

一、引 言

根据时间序列反映出来的相关发展过程、方向和趋势,并进行类推或延伸的时间序列预测,是当前社科研究的核心领域之一。时间序列预测也同时涉及到现代人们生活的许多方面,如商业、环境、能源和交通运输等。其预测方法有单变量、多变量和混合变量组合预测等多种方法。其中,对单个时间序列进行“先分解再组合”的预测方法一直都备受众多研究者的青睐。

时间序列分解预测较为常见的是将序列分解为趋势、季节、周期和随机这四个因素,也有将季节与周期合并且统称季节因素,亦即将时间序列分解为趋势、季节和随机这三个因素。在此基础上,逐项进行预测并通过加法或乘法模型进行组合,进而得到序列的外推预测。此外,还有傅里叶变换分解、小波变换分解和经验模态分解EMD(Empirical Mode Decomposition)等方法。其中,经验模态分解EMD方法是由Huang等提出的,该方法在时间序列预测方面有着十分广泛地应用[1]。EMD方法可用于分析非线性、非平稳序列,具有较高的信噪比和良好的时频聚焦特性。但该方法同时也存在诸多问题,如端点效应(End Effect)和模式混叠(Modal Aliasing)等[2]。随后,Wu等进一步提出了EEMD(Ensemble Empirical Mode Decomposition)方法[3]。Torres等提出了带有自适应噪声的完全集合经验模式分解CEEMD(Complete Ensemble Empirical Mode Decomposition)等方法[4]。但这些在EMD方法基础上的改进都面临着计算量较大,且分解过程中会出现较多伪分量问题[2],同时端点效应(End Effect)和模式混叠(Modal Aliasing)也是其难以根除的掣肘之痛。

近年来,Dragomiretskiy等提出了一个新的适应性分解方法—变分模态分解VMD(Variational Mode Decomposition),该方法主要是由多个自适应的维纳滤波所构成,并且具有良好的噪声鲁棒性。与EMD模型相比,VMD模型拥有强大的数学理论基础,且VMD可以有效缓解或避免EMD中出现的一系列问题,如模式混叠问题等,并且具有较高的分解效率[5]。Lahmiri、Zhu、Gu等通过股价和碳价格预测等问题实证研究表明,VMD模型相较于EMD和EEMD模型的预测精度更高[6-8]。但是VMD分解方法也面临着一个难题,即模态数目K的确定问题。通常在VMD模型中参数K是事先确定的,同时K的大小对序列分解和预测精度都有较大影响。如果K值设置太小,则序列将会不完全分解,若K值设置过大,则序列就会被过度分解,导致高频模式过多。这些都为VMD模型的研究和应用带来诸多困境。

因此,如何确定VMD模型中的参数K就成为了该分解预测方法理论研究和实践应用的关键环节和突破点。对于VMD模型的参数K确定,现有研究通常是基于经验或中心频率观测的方法来确定[9],以及运用预测测试法、皮尔逊相关系数法、空间尺度法、多指标评价法、粒子群优化算法和灰狼算法等。其中,预测测试法是通过不断改变K的个数,使得分解预测达到既定的预测精度,这是一种经验做法,通常参数确定效率低下且难以具有普适性。此外,该方法可能在训练集会达到预定精度,但难以保证在测试集也同样能够达到较高的预测精度[9]。

姜海旭等基于模态分量与原序列的皮尔逊相关系数来确定VMD模型的参数K[10]。皮尔逊相关系数是从线性相关角度来确定分量数目,具有模态数目的选取可解释性和实施简便性等特点,但模态分量与原序列可能存在线性相关,也可能存在非线性相关,因此其参数K的确定单纯以线性相关来进行测度选取,可能会存在一定偏颇。

Ma和Huang等采用了空间尺度和空间尺度谱分段的方法来估计模态分类数K[11-12]。Lian等通过反复搜索K,并采用多指标评价方法来考察分解效果进而确定K的取值[13]。Xiao等将VMD分解方法应用于图像分析,并根据图像大小来确定VMD参数K[14]。Cui等通过希尔伯特转换,确定各模态瞬时频率均值,然后通过载荷曲线曲率作为观察模态瞬时频率的指标,进而比较曲率性能获得最佳值K[15]。然而,这些方法都不能从根本上解决依赖有经验者的先验准则缺陷[9]。

唐贵基等利用粒子群优化算法,对VMD的最佳响应参数进行了搜索研究,进而确定VMD模型参数K[16]。Ren等提出了一种改进的自适应遗传算法来优化确定VMD的参数[17]。通过VMD分解获得分量的熵作为自适应遗传算法的适应度函数,由此利用自适应遗传算法来进行迭代优化,进而确定VMD的参数K。Gu等基于最小平均包络熵作为拟合值,并通过灰狼算法来确定VMD参数取值[8]。这些从算法层面上来确定VMD模型的参数K,逻辑严密且通常具有较好的自适应性。但算法层面的解决方法通常都存在初始参数确定依据先验、收敛速度慢和易陷入局部最优等问题。

总体而言,关于VMD模型参数K的确定,已成为目前VMD模型理论与应用研究的一个重要方向,引起了诸多研究者的广泛关注,同时也取得了一定的研究成果。然而,无论是皮尔逊线性相关还是谱分析思想,抑或是各种算法而实现的参数优化,都存在着一些难以解决的新问题,如模型预测精度不够以及参数确定收敛速度慢和易陷入局部最优等问题。其实,VMD模型的模态分量是基于原序列的分解而得,其模态数目K也应是结合目标设定下各分量特征以及各分量与原序列的关联紧密程度来确定。因此,要确定参数K的具体数值,就需要考察各个分量关于原序列的分解特征,以及各分量与原序列的线性或非线性的相关性。对此,本文尝试借助测算变量相关性的最大信息系数MIC(Maximal Information Coefficient)和主成份降维思想,构建加权MIC方法,通过设置阈值以及计算加权后MIC的累积贡献来辨识和确定VMD模型的参数K,助力于推进VMD模型的理论研究与实践应用。

二、VMD模型与加权MIC参数确定方法

(一)VMD模型

变分模态分解VMD模型是一种自适应信号处理方法[5],该方法能够自适应地将序列S(t)分解成K个模态分量uk,并通过迭代搜寻变分模态的最优解,不断更新各模态函数及中心频率,得到若干具有一定带宽的模态函数。VMD算法将分解转化为两个步骤,即构造变分问题和求解。变分问题的约束可由下式(1)来描述:

(1)

其中,S(t)为原始序列,{uk}={u1,u2,…,uk}是模态分量,{ωk}是{uk}的中心频率,∂(t)是脉冲函数,K是模态分量的数目。

求解公式(1),引入拉格朗日乘数λ和二次惩罚因子α(作用是降低高斯噪声干扰)将约束变分问题转变为非约束变分问题,得到增广拉格朗日表达式见下式(2)所示:

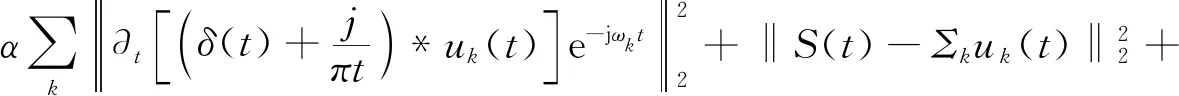
(2)

利用交替方向乘子迭代算法,结合傅里叶等距变换,优化得到相应的模态分量和中心频率,并搜索增广拉格朗日表达式的鞍点。交替寻优迭代后的uk、ωk和λ表达式如下:

(3)

(4)

(5)

(6)

通过VMD分解,可以获得K个不同中心频率的模态分量,且同时随着uk的不断迭代分解,中心频率在作差的过程中也表现为不断衰减。从参数角度而言,模态分量数K是至关重要的,而二次惩罚因子、噪声容忍度和收敛误差对分解结果影响相对较小,且为了便于比较分析,本文将二次惩罚因子α、噪声容忍度τ和收敛误差ε这三个参数均设置为默认值,分别为α=2 000,τ=0,ε=1e-7。另外,迭代次数N默认设定为500。

(二)MIC方法

测度变量间依赖关系的过滤或筛选方法(Filter Methods),通常是基于距离、一致性、相关性或特征信息来进行的。其中,信息度量被认为是最有效的测度之一,通过此种方式可以捕获变量间线性或非线性相关关联特征。为了探索变量间多种关联特性,Reshef等提出了最大信息系数(MIC)方法[18]。MIC不仅可以测度变量间线性和非线性等相关性,而且还可以在不局限于某特定函数类型下捕获其他多种有趣的关联。另外,MIC方法可以辨识出不同噪声水平下相同类型的关联特性。因此,MIC凭借其独特优势在诸多领域中都有着十分广泛的应用。

MIC的相关性测度源于互信息(Mutual Information)的应用。互信息是一种信息度量方法,可以看作是一个随机变量中包含另一个随机变量的信息量,抑或是一个随机变量由已知的另一个随机变量而减少的不确定性。

假设给定一个数据集D,其中包含x和y这两个二维数据变量,x与y的联合概率分布为p(x,y)。x与y的互信息则定义为:

(7)

x和y彼此关联性越强,I(x,y)的值越大。但由于联合概率分布p(x,y)通常获取较为困难,对此较为简单的处理方法是对数据进行分组,亦即通过对x-y散点图中叠加一个矩形网格,然后将每个连续的x(或y)分配给对应的列x组(或行y组),得到新的分组后的X与Y,在分组基础上(数据离散化)两个变量的互信息计算公式为:

(8)

通过分组方式来简单估计联合概率分布容易造成I(x,y)被系统性高估。因此,Reshef等在互信息基础上,进一步将测度两变量相关性的MIC定义为:

(9)

其中,B为x和y分组网格总数的限制,通常是样本容量N的0.6或0.55次方[18]。另外,MIC的取值在0～1之间。

(三)加权MIC与模态分量数K的确定

对序列进行VMD分解可以得到一系列模态分量,各模态分量对应不同的中心频率,且在一定程度上彼此独立,但随着模态分量数目的增加,原序列分解后中心频率会呈现出衰减趋势,同时各个分量对原序列的方差分解也随着既定幅度的数据变换和中心频率衰减这两者共同作用而表现出递减趋势。

MIC方法是基于网格化概率分布形式来考察变量间的相关特性,对中心频率衰减的反映往往较为敏感,但对各个分量关于总体方差分解的反映则相对缺乏灵敏性,由此可能会导致MIC出现厚尾现象,亦即难以由MIC的信息测度来准确判断边缘分量,从而也难以确定分量数目K。

因此,为进一步体现方差分解和中心频率两者的衰减特征,以及避免MIC厚尾而难以确定分量数目K的问题,本文尝试通过以各分量的方差贡献为权重来对MIC进行加权,在反映各分量方差分解特性的同时避免厚尾问题,进而快速有效地实现VMD模型分解参数K的确定。具体计算步骤如下:

第一步,假定VMD模型对序列S进行分解,得到初始化K个的模态分量uk(k=1,2,…,K)。由此我们首先利用MIC来测度各分量与原序列S的相关性。

第二步,将每一个分量,如第k个分量uk(k=1,2,…,K),与序列S进行网格化处理,并求出最大的互信息值。最大互信息值是基于落在各个网格的点数来确定各行与各列的边缘概率p(S)、p(uk)和联合概率p(S,uk),并基于公式(8)计算网格对应的互信息值I(S,uk),并选取出网格最大的互信息值。

第三步,对最大的互信息值进行归一化处理。亦即以最大互信息值除以log2(min(|S|,|uk|)),得到各个网格归一化处理结果。

第四步,选取出归一化结果中的最大值,进而得到分量uk与序列S的MIC(S,uk)。

第五步,重复上述步骤,得到K个分量与序列S的MIC值,分量对应的MIC值越大,该分量与原序列相关性程度越高。

第六步,计算各分量的方差贡献。对此,本文利用主成分分析思想,主成分是基于变量间相关性测度来实现选择性降维(通过方差累积贡献率)。而VMD分解后的分量数目确定也与此雷同,可以通过满足信息贡献率条件来确定边缘分量。因此,基于主成分降维思路,对K个分量进行类似的“降维”处理。首先通过计算得到K个分量的相似矩阵,由此获得K个相似矩阵的特征值ek(k=1,2,…,K),通过特征值ek计算得到每个分量的方差贡献率vcuk=ek/Σkek。

第七步,计算各个分量的加权MIC值和累积贡献率。将分量的方差贡献率作为权重,得到第k个分量加权MIC值:uvMICk=vcuk×MIC(S,uk)。第k分量的贡献率为:c_uwMICk=uwMICk/ΣkuwMICk,并由此可以计算各个分量的累积贡献率cul_uwMICk。

第八步,调整K值,重复上述步骤,得到不同K值下的加权MIC值和累积信息贡献率。

第九步,K值的确定。主要通过两个条件来确定:一是分量的累积信息贡献率,如可设定累积贡献率阈值为99%;二是累积信息贡献曲线的收敛临界点,对此可通过该曲线的曲率来判定。随着K值的增加,累积贡献百分比将逐渐收敛至1。由此可根据累积信息贡献率的离散点来计算其曲率并考察曲线的收敛情况,亦即确定贡献曲线收敛临界点,进而由此来确定参数K。常见的离散点计算曲率公式如下:

(10)

其中,x′(t)和y′(t)表示累积贡献离散点对应坐标函数的一阶导数,x″和y″表示二阶导数。基于曲率来判断累积贡献收敛情况和收敛时K值的标准是:随着K的变化,当某处曲率绝对值始终小于某一阈值,且后续曲率持续处于降低态势(表明曲线是逐渐收敛的),则该处为累积信息贡献曲线的收敛临界点,其对应的最小K值即为满足条件的最优参数值。对于曲率绝对值的阈值设定,可以根据实际情况的精细要求不同来进行确定,本文设定此阈值为0.001。总之,本文K值的最终确定是基于各分量累积信息贡献大于99%,且累积贡献曲线收敛情况下曲率小于等于0.001来确定参数K。

第十步,评价。对加权MIC方法确定参数K的效果,主要从两个角度来进行评价:一是加权MIC方法与皮尔逊相关系数、空间尺度谱分段等其他确定VMD模型参数K的方法进行比较分析;二是从序列预测效果角度来考察。通过与其他预测模型比较,进一步考察加权MIC确定参数K下的预测效果。预测效果的比较指标是选取序列预测的均方误差MSE(Mean Square Error)来作为误差衡量标准。MSE的计算公式如下:

(11)

三、算 例

在加权MIC方法构建基础上,进一步选取实际数据对该方法进行检验分析。序列长短是影响该序列分解的关键。对此,本文选取了两种数据,一是序列较长的美元兑人民币汇率日数据,二是序列相对较短的消费者信心指数(CCI)月度数据,以此来检验加权MIC方法在不同时间序列下VMD模型参数K的辨识效果。

(一)算例样本数据

1.美元兑人民币汇率

美元兑人民币汇率的样本指标为汇率的日线收盘价格(Ex_rate)。数据样本期为:2009年1月1日—2020年1月1日。观测样本容量为2 870个。数据来源于中国人民银行官网的外汇数据。样本数据的趋势图及相关描述统计数据见下图1和表1所示。在样本期内,美元兑人民币汇率的最大值为7.178 9,最小值为6.041 2。样本数据标准差为0.288,峰度为-1.313 3,偏度为0.044 2,样本数据总体呈现为右偏且较为平坦的数据形态。

图1 美元兑人民币汇率日线样本数据

表1 Ex_rate和CCI描述统计分析

2.中国消费者信心指数

选用样本期为2008年1月—2019年12月的中国消费者信心指数(CCI)的月度时间序列数据,样本容量为144。数据来源于EPS数据库。样本数据的趋势图与相关描述统计分析见图2和表1所示。在样本期内,CCI的最大值为126.6,最小值为86。样本数据标准差为10.410 3,峰度为-0.376 4(<0),偏度为0.239 0,样本数据总体呈现出存在波动相对较大的右偏分布形态。

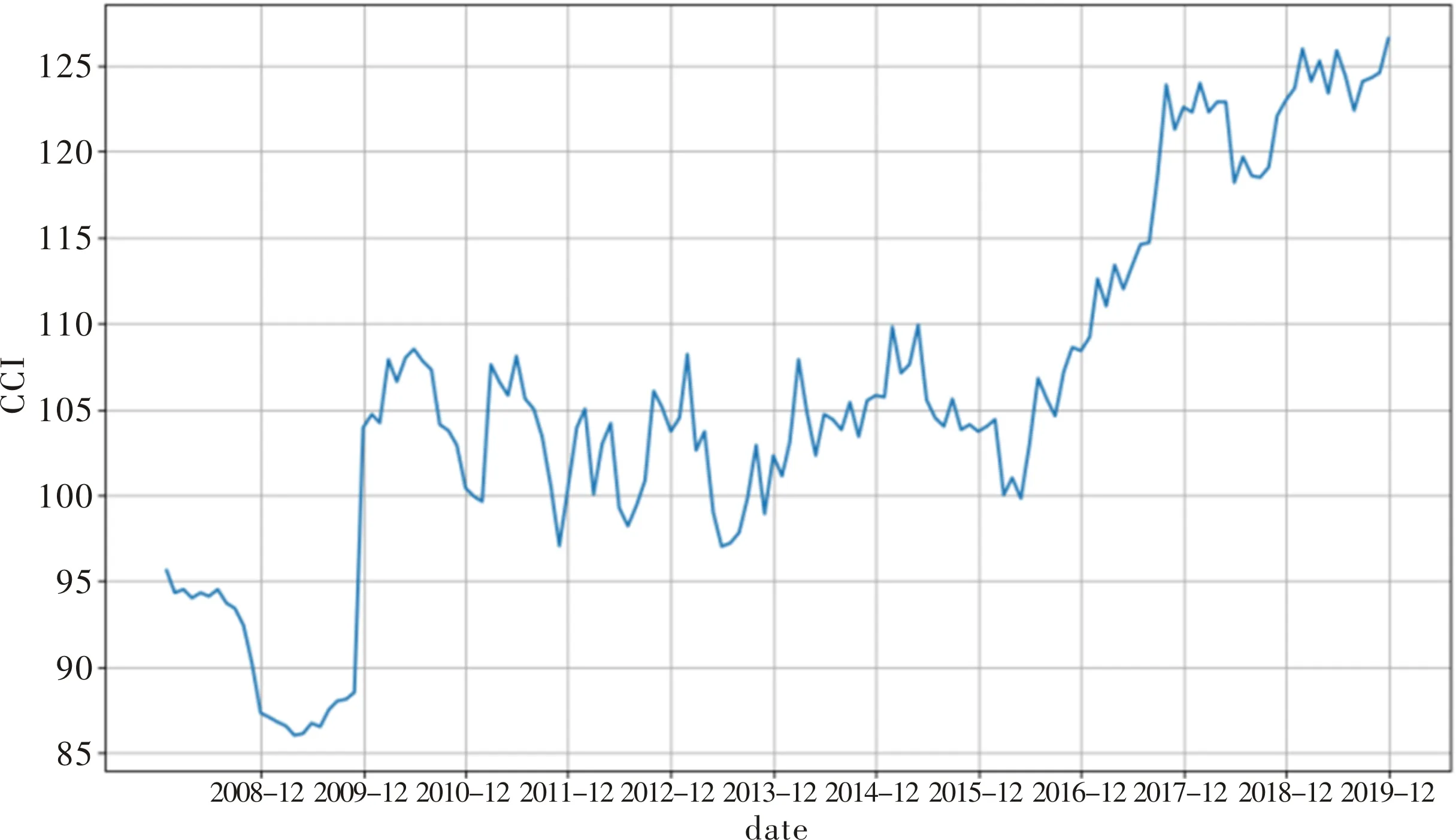
图2 CCI样本数据

(二)基于加权MIC模型的VMD分解参数K确定

针对上述两个算例的时间序列样本数据,运用VMD和加权MIC模型进行参数确定分析和检验。具体步骤主要包括三个方面:一是算例数据的VMD模型初始分解;二是计算不同K情况下序列分解的各分量MIC值和方差贡献率,以及计算方差贡献为权重的加权MIC值、累积信息贡献和累积信息贡献曲线的曲率;三是通过曲率变化的判断准则最终确定参数K。

1.美元兑人民币汇率算例

首先,序列初始分解。借鉴Lahmiri(2016)的做法,将算例序列从分量数K=2,3,…,20进行逐项的VMD模型分解,得到不同参数K的系列分量BIMF。其次,在序列分解的基础上,计算不同K情况下各分量的MIC和方差贡献率。汇率样本数据的各分量MIC和方差贡献计算结果见表2和表3所示。

表2 汇率数据不同K下的各分量MIC值

由表2可以看出,在不同分量参数K情况下,第一个分类BIMF1的MIC值始终都较大,此后随着分量数目增多,除残差外其余分量的MIC值都呈现出递减趋势,且递减幅度逐步放缓。由上述数据结果可以看出,我们难以通过MIC值的简单截断来确定参数K的取值。对此,我们进一步计算得到不同K值下各分量的方差贡献率(见表3)。

表3 汇率数据分解在不同K值下各分量的方差贡献率

由表3的结果可看出,与各分量的MIC值情况类似,不同K值下汇率数据的第一分量BIMF1的方差贡献都较大且均超过了0.9,远大于其他分量贡献率,此后各分量的方差贡献迅速衰减,通过如此“头重脚轻”的方差贡献率来简单确定参数K亦存在较大困难。因此,我们尝试利用各分量MIC和方差贡献率这两个方面的信息,计算以方差贡献率为权重的加权MIC,以此来考察确定参数K,可能会收到更好的效果。

对此,通过计算各分量MIC与相应方差贡献率的乘积,并进行归一化处理得到不同K情况下加权MIC的累积比率数据,见表4和图3所示。

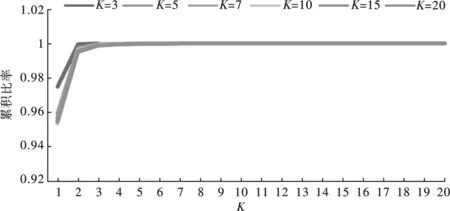
图3 K=3,5,7,10,15和20的加权MIC累积比率

表4 不同K情况下加权MIC的累积比率

由表4和图3可以看出,不同K值情况下,以分量方差贡献加权的MIC累积比率分布形态相似,且曲线收敛的规律性已昭然若揭,在数步累积后迅速收敛至1。

因此,进一步结合曲率计算,可以快速判断出曲线收敛的临界点以及其所对应的参数K值。通过前述判断条件:加权MIC累积贡献比率超过99%,且累积比率稳定收敛下的曲率临界点来判断参数K,对此相应的曲率计算结果见表5所示。由表5可以看出,在不同分量K情况下,最终K=4时曲率绝对值均小于0.001,且此后曲率都逐渐降低,曲线处于平滑收敛状态。由此初步可以确定VMD模型参数K=4。另外,当K从5增加到20来看,K>4之后的分量加权MIC贡献累积比例都不足0.000 6,总体贡献微乎其微。因此,最后确定VMD模型参数K为4。

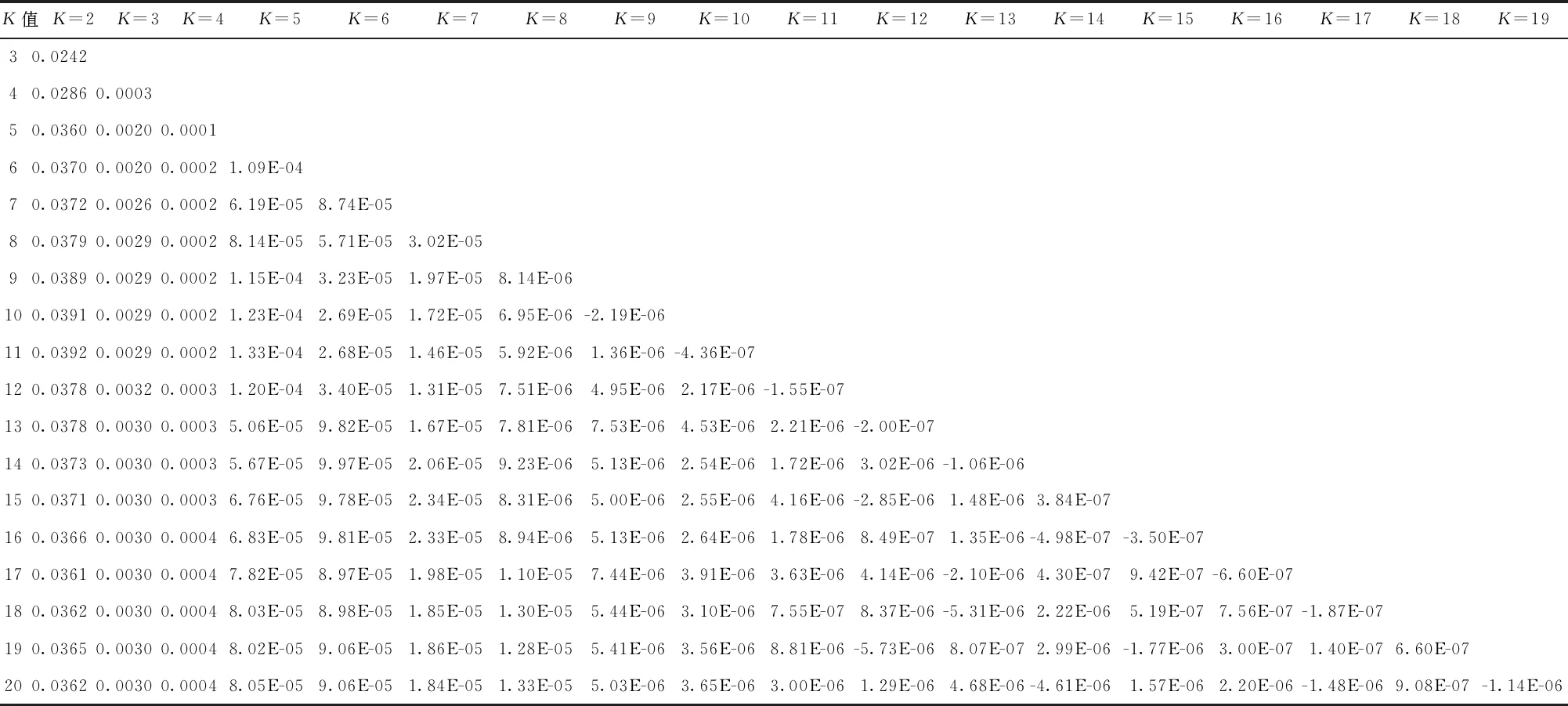
表5 汇率数据不同K情况下累积信息贡献曲线的曲率数值

最后检测K=4的分解效果。主要从两个方面来检测评价:一是加权MIC方法与其他VMD模型参数K确定方法的比较;二是考察参数K=4情况下序列预测的结果比较。

对此,加权MIC方法与皮尔逊相关系数法、空间尺度谱分段方法(Huang等,2019)、自适应遗传算法(Ren等,2018)和灰狼算法(Gu等,2020)这5种方法,对确定VMD模型参数K的结果见表6。

表6 加权MIC方法确定参数K与其他方法比较

由表6可以看出,除皮尔逊相关系数法外,加权MIC、空间尺度谱分段、灰狼算法和自适应遗传算法均确定参数K为4,且K=4时预测美元兑人民币汇率后10期的均方误差MSE小于K=3,说明参数K=4预测效果较好。另外,从平均迭代次数和达至收敛的运算时长方面来看,加权MIC方法平均迭代次数最少且用时最短,该参数确定方法优势较为明显。

进一步从序列的预测效果来考察加权MIC方法的参数确定效果。一是基于加权MIC的VMD模型与ARIMA、EMD和EEMD的模型预测比较。二是不同VMD模型参数K下的预测结果比较。

通过参数筛选,ARIMA模型的关键参数自相关滞后、差分和移动平均阶数最终确定为(2,1,2),即ARIMA(2,1,2)模型。EMD、EEMD和VMD模型的预测都是在分量基础上,借助其他预测模型来对各个分量进行预测,最后对各分量预测结果加总得到序列整体预测值。对此,在模型分解基础上,本文统一选取兼顾时间序列长短期记忆的LSTM(Long-Short Term Memory)模型来对各个分量进行预测。各分量的预测LSTM模型参数统一为隐层2个、隐层神经元个数为10个,学习率0.000 5。由此进一步得到各个模型对美元兑人民币序列后10期的预测结果见表7所示。

由表7可以看出,加权MIC确定参数K=4时,相较于K=2和K=3时预测MSE值下降明显,而对于K=5和K=6时预测MSE并未出现明显改进,说明了参数K=4相较于其他参数有较好的预测效果且分量数最少。另外,参数K=4的VMD模型分解预测误差也相应小于ARIMA、EMD和EEMD模型,模型预测效果较好。总体而言,加权MIC对VMD模型的参数K确定效果非常突出。

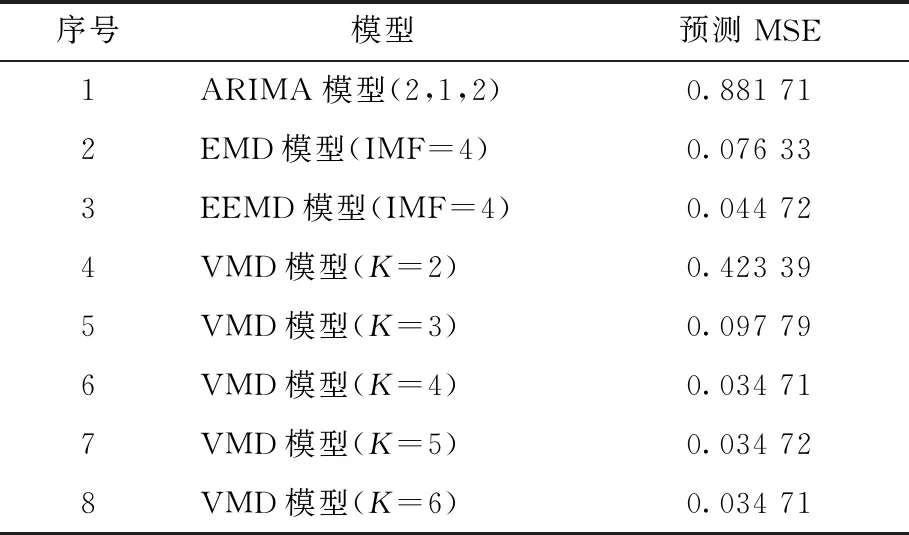
表7 加权MIC方法与ARIMA等模型的预测结果比较

2.CCI算例

在对CCI时间序列样本数据进行参数K=2,3,…,20的VMD模型初始分解基础上,得到各分量序列BIMF。在序列分解基础上,进一步计算各分量的MIC值和方差贡献率。具体结果见表8和表9所示。

表8 CCI序列数据不同K下的各分量MIC值

由表8可以看出,在不同分量K情况下,与汇率算例情况类似,第一个分类BIMF1的MIC值始终都较大,此后随着分量数目增多,除残差外后续分量的MIC值基本都呈现出递减趋势,且递减幅度逐步放缓,仅以MIC值难以进行截断来确定参数K值。

不同K值下各分量方差贡献率结果见表9所示,可以看出,与分量MIC值情况类似,CCI数据的第一分量BIMF1的方差贡献都相对较大,且都超过了0.5,也大于其他分量贡献,此后各分量的方差贡献迅速衰减。但引起注意的是,随着K值的增加,第一分量的方差贡献呈现下降趋势,最后数期的方差贡献基本稳定在0.52左右。因此,单纯依赖方差贡献来进行K值的确定也难以实现。

表9 不同K值下各分量的方差贡献率

进一步计算分量贡献率加权的MIC值,通过各分量MIC与相应方差贡献率的乘积,并进行归一化处理得到不同K情况下加权MIC的累积比率数据见表10和图4所示。

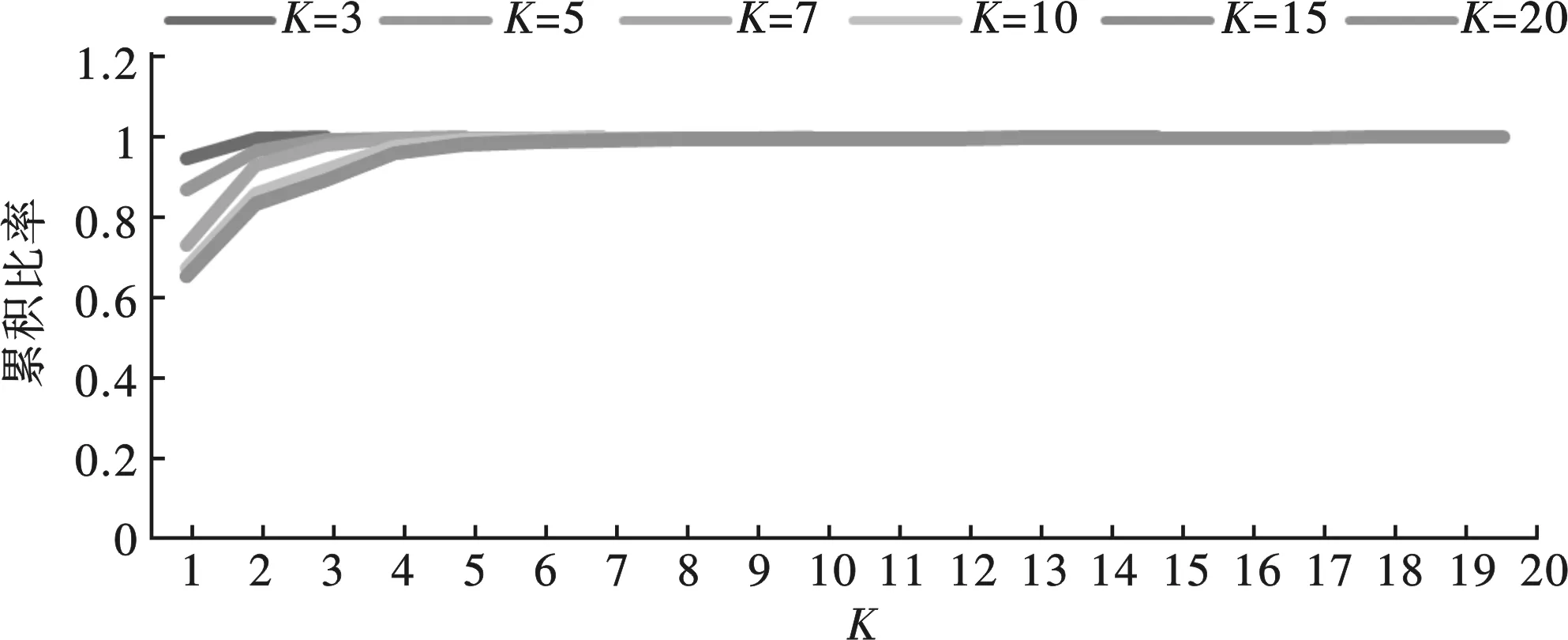
图4 K=3,5,7,10,15和20的加权MIC累积百分比

表10 不同K情况下加权MIC的累积比率

由表10和图4可以看出,不同K值情况下,分量方差贡献加权的MIC累积比率分布形态都十分相似,在数步累积后迅速向1收敛。与汇率算例相比,CCI分解后累积信息贡献收敛的速度相对慢一些。

对此,进一步结合曲率计算来判断出曲线收敛的临界点及其所对应的参数K值。通过前述的判定条件:满足加权MIC累积贡献比率超过99%,且累积比率稳定收敛下的曲率临界点对应的最小K值为最优值。由表10可以看出,K大于等于7之后累积贡献都大于99%。同时进一步计算累积信息贡献曲线的曲率,结果见表11所示。由表11可以看出,在不同分量K情况下,K=5时曲率大部分都小于0.001,但随后在K=6时曲率出现震荡而部分曲率大于0.001,直至K=8时曲率绝对值基本都小于0.001,且此后曲率呈现持续降低态势,满足判定要求。此外,当K从9增加到20来看,K>8之后的分量加权MIC贡献累积比率均不足0.008,总体贡献微乎其微。因此最后判定VMD模型的参数K为8。

最后检测参数K=8的分解效果。首先,在参数确定方法的比较方面,加权MIC方法与皮尔逊相关系数法、空间尺度谱分段方法、自适应遗传算法和灰狼算法的参数确定结果见表12所示。

由表12可以看出,加权MIC方法和灰狼算法均确定参数K=8。皮尔逊相关系数法、空间尺度谱分段方法和自适应遗传算法在参数K上均有不同,分别为6、7和10。在序列后10期的预测误差MSE方面,加权MIC法虽略大于自适应遗传算法(参数K=10),但其平均迭代次数和收敛运算时长都明显优于其他参数确定模型。

表12 加权MIC方法确定参数K与其他方法比较

进一步考察加权MIC确定参数K的序列预测效果。将加权MIC参数确定下的VMD模型与ARIMA、EMD和EEMD模型,以及不同K下的VMD模型进行比较研究。其中,ARIMA模型的关键参数自相关滞后、差分和移动平均阶数最终确定为ARIMA(1,1,0)。各分量的预测LSTM模型的参数仍统一为隐层2个、隐层神经元个数为10个,学习率0.000 5。各模型对CCI序列后10期的预测结果见表13所示。

由表13可以看出,加权MIC确定参数K=8时,相较于K=6和K=7时预测MSE值下降明显,而K=9和K=10时预测MSE并未出现明显改进,加权MIC确定的参数K=8预测效果较好。另外,参数K=8的VMD模型分解预测误差也明显小于ARIMA、EMD和EEMD模型,预测效果较好。总之,加权MIC对VMD模型的参数K确定效果优异。

表13 加权MIC方法与ARIMA等模型的预测结果比较

四、结 语

变分模态分解VMD是基于自适应的维纳滤波思想,通过不断迭代从原序列中剥离出分量,进而实现对序列的分解和特征表达。然而,现实序列数据中,不同序列之间的数据特征往往千差万别。那么,如何较好地实现特征表达和信息提取,并在此基础上确定最优分量数,亦即实现参数K值的最优辨识,是影响该方法理论研究和实践应用的一个关键,也是诸多研究者关注该模型方法的一个焦点问题。

对此,本文针对VMD模型参数K的辨识问题,尝试构建了基于分量方差贡献和最大信息系数MIC的加权MIC方法,并通过美元兑人民币汇率和消费者信心指数这两个实际数据的算例进行了分析检验研究。结果表明,针对不同数据特征序列,单纯的MIC方法或分量方差贡献都难以辨识出VMD分解的最优参数K值,而加权MIC则对于参数K的辨识确定具有良好效果,该方法可以自动辨识出序列分解要求下的最优K值,亦即在保证信息提取基础上有效地确定了可以舍弃的相对冗余分量。换言之,针对不同特征序列,通过初始分解,分量MIC和方差贡献计算,以及累积方差贡献曲线的临界点判定等,都可以实现流程化计算和识别,进而实现最优参数K的确定和模型应用,该方法在针对不同数据特征序列的应用方面具有一定的普适性。