SM4 算法的量子实现*

林 达, 向泽军, 张若琳, 张莎莎, 曾祥勇

湖北大学数学与统计学学院应用数学湖北省重点实验室, 武汉 430062

1 引言

随着量子信息科学的快速发展, 量子技术特别是量子计算机的研究取得了突破性进展. 量子计算机具有并行处理信息的能力, 这种特性使得一些经典计算机中的困难问题在量子场景下很容易被解决, 从而给公钥密码的安全性带来严重威胁. 特别是Shor 算法[1]的提出, 这一开创性工作可以有效地用来进行大整数因子分解和求解离散对数, 使得目前基于上述困难性问题的经典密码安全性受到严重挑战. 目前大规模通用量子计算机远未普及, 而且量子计算机的性能及相关技术的发展也具有一定的不确定性, 因此, 完成由现有的经典密码算法向后量子密码算法的过渡仍有许多问题亟待解决. 美国国家标准与技术研究院(National Institute of Standards and Technology, NIST) 于2016 年启动了后量子密码算法标准的征集工作[2]. 不同于经典密码算法安全强度的定义方式, 针对量子密码算法, NIST 根据AES[3]和SHA-3[4]提供的安全强度定义了一系列广泛的安全强度类别, 分别与穷举攻击上述经典密码所需量子资源有关. 由于Grover 算法[5]在遍历一个无序集合时能够实现二次加速, 研究经典密码算法利用Grover 算法穷举密钥的量子实现开销是当前量子密码领域的研究热点.

与经典电路不同, 量子电路具有可逆性特点. 在量子电路中实现经典电路逻辑门时, 可以分别使用Toffoli 门和CNOT 门模拟经典电路中的与运算和异或运算, 因此经典电路的功能都可以使用量子电路实现. 考虑到量子计算机的不确定性, 以节约量子比特为前提设计高效的量子电路是研究经典密码算法量子优化实现的一个主要关注点. 此外,由于Toffoli 门的实现代价远大于CNOT 门、Hadamard 门等Clifford门集中的通用逻辑门, 量子电路中消耗的Toffoli 门数量以及电路Toffoli 深度是评估量子电路实现代价的一个主要参考指标. 目前, 对对称密码算法量子优化实现的探索主要以AES 算法为研究对象[6–10]. 2016年, Grassl 等人[6]首次系统地提出了一种利用Grover 算法穷举搜索AES 密钥的量子实现方案, 并从量子电路大小、量子比特数量、量子电路深度等方面全面分析了该穷举攻击的量子资源开销, 其中量子电路的大小与整体电路消耗的通用量子逻辑门数量有关. 随后, Almazrooie 等人[7]针对AES-128 设计了一种可逆量子电路, 该电路采用Grassl 等人设计的zig-zag 结构[6]以节约量子比特. 不同于文献[6] 和文献[7] 基于有限域上的乘法以及求逆运算构造AES 算法S 盒的优化实现, Langenberg 等人[8]利用基于塔域分解生成的AES 算法S 盒的经典实现[11], 设计了一组全新的AES 量子优化实现电路并评估了利用Grover 算法进行穷举攻击的量子资源开销.

在统计电路的量子资源开销时, 上述研究主要关注量子比特以及量子逻辑门的使用数量. 近年来, 考虑到量子纠错码的应用, 越来越多的研究同时关注了量子电路的另一个评价指标: depth-times-width 值,即量子电路中量子比特数与电路深度之积[9,10]. 2020 年, Jaques 等人[9]以AES 和LowMC[12]为例研究了在电路深度受限情形下进行量子密钥搜索攻击的代价. 在ASIACRYPT 2020 上, Zou 等人[10]提出了一种改进的zig-zag 结构, 该结构基于对S 盒代数结构及其经典实现的进一步研究, 优化了AES 算法量子实现电路消耗的量子比特数目以及电路的depth-times-width 值.

SM4 算法[13]是我国商用密码算法标准, 并于2021 年正式成为ISO/IEC 国际标准. SM4 算法采用了与AES 算法类似的S 盒设计方法, 鉴于基于塔域结构构造AES 类算法S 盒的实现是目前较为高效的方法, 通过研究SM4 算法S 盒的代数结构设计其优化实现被广泛关注[14–17]. Bai 等人[14]采用Paar 提出构造同构映射的方法[18], 利用多项式基将F28表示成F24的二次扩域, 由此将F28上的元素分解为系数属于F24的线性多项式, 最终通过将F24上的运算进一步分解为一系列F22上的操作实现有限域上的求逆运算. 利用组合逻辑电路, Abbasi 等人[15]研究了SM4 算法S 盒适用于如智能卡等面积受限环境的紧凑实现, 并基于正交基的塔域表示F28→((F22)2)2提出了一种SM4 算法S 盒的新型组合结构. 2015年, 一种基于(F24)2上的复合域设计的SM4 算法S 盒新型结构被提出[16], 与之前的实现相比, 利用该结构能有效减少硬件实现所需异或门数量. 通过有限域上乘法逆及其仿射等价类的面积优化实现, Wei 等人[17]研究了基于正规基F28上逆的塔域表示, 同时利用既有简化组合逻辑电路的技术, 全面研究了所有可能正交基下F28上求逆运算的塔域表示, 并给出了SM4 算法S 盒更紧凑的硬件实现.

1.1 本文贡献

根据对塔域分解技术生成的S 盒经典实现的研究, 本文介绍了一种结合即有启发式算法设计SM4 算法S 盒的量子实现新方法, 该方法为构造高效的S 盒量子实现提供了新思路. 利用该方法, 本文设计了一种对S 盒输出量子比特初始值无任何要求的SM4 算法S 盒的量子优化实现方案; 进一步, 基于对SM4算法合成置换不同实现方法的探索, 本文提出了一种通过将线性变换前移以改进置换T和T′的量子实现优化技术. 利用该技术, 本文分别为SM4 算法的密钥扩展算法和轮函数设计了一种量子优化实现方案, 基于此, 本文针对SM4 算法, 结合其加密轮函数将合成置换输出异或到其中一个分支的特性, 提出了一套能有效节约量子比特的量子实现整体结构; 此外, 通过系统地研究电路并行处理的S 盒数量对SM4 算法不同实现方案的量子比特数以及depth-times-width 值等指标的影响, 本文对比了基于zig-zag 结构实现的AES-128 算法量子电路, 并提出了一种在上述指标上均优于AES-128 的SM4 算法量子实现方案; 最后,本文首次提出了结合Grover 算法对SM4 算法进行量子密钥穷搜的量子电路, 并分析了SM4 算法抗量子穷举攻击的安全强度. 本文的研究结果表明, 在考虑量子比特开销和depth-times-width 值等指标的情形下, SM4 算法抵抗量子穷举攻击的安全性要弱于AES-128 算法.

1.2 本文组织结构

第2 节引入本文所使用的符号, 并简要介绍Grover 算法和SM4 算法等预备知识. 第3 节给出SM4算法不同子部件的量子实现方案. 第4 节针对SM4 算法的密钥扩展算法和轮函数设计了相应的量子电路.第5 节介绍利用本文设计的SM4 量子实现方案进行量子密钥穷举的量子电路, 并评估该攻击的量子资源开销. 第6 节对本文的工作进行总结.

2 预备知识

本章介绍本文使用的符号、Grover 搜索算法以及SM4 算法及其S 盒的经典实现等背景知识.

2.1 符号说明

2.2 Grover 算法

Grover 算法的具体流程如图1 所示, 其中H为Hadamard 门.

图1 Grover 算法Figure 1 Grover algorithm

由文献[19] 式6.6 可知, 上式可以写为:

利用Grover 算法遍历无序集合的具体步骤如下:

(a) 将Uf作用于输入量子态.

(b) 应用H⊗n.

(c) 相位翻转.

(d) 应用H⊗n.

(3) 测量电路前n个量子比特位.

2.3 SM4 算法

SM4 算法分组长度与密钥长度均为128 比特, 采用32 轮非线性迭代结构, 其整体结构如图2 所示.

图2 SM4 算法流程图Figure 2 Procedure of SM4

2.3.1 轮函数

2.3.2 密钥扩展算法

记SM4 算法加密密钥为MK=(MK0,MK1,MK2,MK3)∈(F322)4, 则第i轮轮密钥的生成方式为:

其中CKi为给定常数,i= 0,1,··· ,31. (K0,K1,K2,K3) 初始化为(MK0⊕FK0,MK1⊕FK1,MK2⊕FK2,MK3⊕FK3), FKj(j= 0,1,2,3) 为系统参数. 变换T′由非线性变换τ和线性变换L′复合而成,与算法轮函数中T变换类似, 记变换τ的输出为B, 则L′的输出C为

2.3.3 SM4 算法S 盒的经典实现

SM4 算法S 盒的硬件实现被广泛研究[14–17], 表1 列出了各参考文献提出的SM4 算法S 盒实现方案中不同逻辑门电路的消耗数量.

表1 SM4 算法S 盒的硬件实现开销Table 1 Hardware cost to implement S-box of SM4

文献[17] 利用塔域分解技术以节约硬件面积为出发点研究了AES 类算法S 盒的优化实现, 并给出了SM4 算法S 盒的硬件实现方案(见文献[17] 附录C). 该方法将SM4 算法S 盒的实现分解为5 个部分,分别由以下5 个函数表示.

函数Input() 为SM4 算法S 盒实现中的第一层线性部分. 函数Input() 的输入为S 盒的输入, 记为(x0,x1,··· ,x7), 其输出为(y0,y1,··· ,y17), 且输出可如下计算:

函数Top() 为SM4 算法S 盒实现中的第一层非线性部分, 其输入为函数Input() 的输出, 即(y0,y1,··· ,y17), 其输出(p0,p1,p2,p3) 可如下计算:

函数Middle() 为SM4 算法S 盒实现中的第二层非线性部分, 其输入为函数Top() 的输出, 即(p0,p1,p2,p3). 记函数Middle() 的输出为(l0,l1,l2,l3), (l0,l1,l2,l3) 可如下计算:

函数Bottom() 为SM4 算法S 盒实现中的第三层非线性部分, 函数Input() 的输出(y0,y1,··· ,y17)以及函数Middle() 的输出(l0,l1,l2,l3) 作为其输入, 其输出(e0,e1,··· ,e17) 可如下计算:

函数Output() 为SM4 算法S 盒实现中的第二层线性部分, 其输入为函数Bottom() 的输出, 即(e0,e1,··· ,e17), 其输出即为S 盒的输出(s0,s1,··· ,s7).

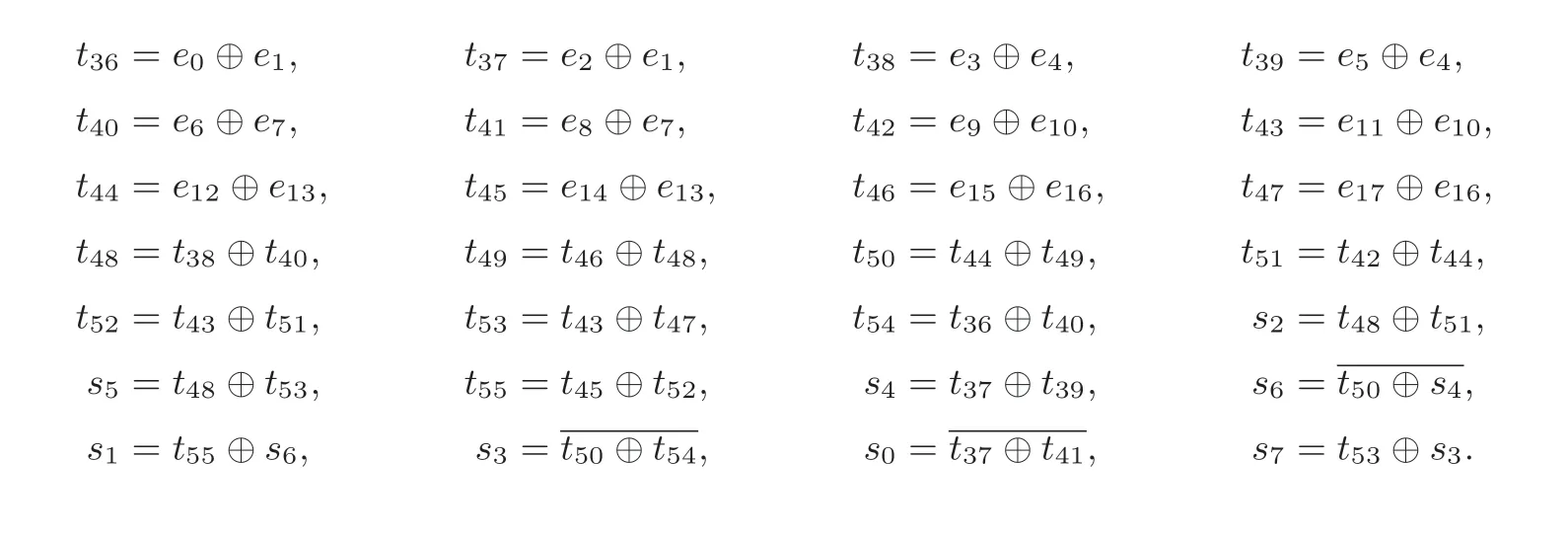
3 SM4 算法子部件的量子实现

本节给出SM4 算法子部件的量子实现构造方案.

3.1 SM4 算法线性变换的量子实现

SM4 算法状态位为128 比特, 分为4 个32 比特长的字进行处理. 算法轮函数(式(2)) 和密钥扩展算法(式(3)) 包含32 比特的异或, 均可由32 个CNOT 门并行实现.

合成置换T中的线性变换L可以表示成F2上32×32 的可逆矩阵, 具体如下:

其中,B1,B2,B3分别为:

同理, 密钥扩展算法中的L′变换可以由F2上32×32 的可逆矩阵表示, 具体如下:

其中,E为F2上8×8 的单位矩阵,分别为:

利用LUP 分解实现算法线性层是目前研究AES 算法量子优化实现时普遍采用的方法. 然而, 该方法生成的实现所需异或运算较多、电路异或深度较大. 2020 年, Xiang 等人[20]基于矩阵分解理论提出了一套搜索矩阵优化实现的启发式算法, 该算法同样能在不额外引入新变量的前提下搜索F2上二元矩阵的优化实现. 上述两种实现方法均生成矩阵的in-place 实现, 从而可借助CNOT 门模拟异或操作将利用上述方法得到的经典实现转换为量子实现. 与LUP 分解给出的实现相比, 通过文献[20] 中的算法获得的实现在异或门电路数以及电路深度方面具有一定优势. 因此, 本文采用文献[20] 中提出的算法实现SM4 算法的线性子部件(包括线性变换L和L′), 其中线性变换L对应矩阵的实现消耗83 个异或门电路, 电路深度为6, 线性变换L′对应矩阵的实现消耗78 个异或门电路, 电路深度为7. 线性变换L和L′的具体实现见附录中表4 和表5.

3.2 SM4 算法S 盒的量子实现

本节给出SM4 算法S 盒的量子实现方案:|x〉|b〉|0a-8〉 →|x〉|b ⊕S(x)〉|0a-8〉, 其中x,b,S(x)∈F28.

由本文第2.3.3 节所示SM4 算法S 盒的经典实现可知, 不同函数的输入输出之间存在一定的联系, 如函数Output() 建立了算法S 盒的输出(s0,s1,··· ,s7) 与变量y0,y1,··· ,y17以及变量l0,l1,l2,l3之间的关系. 上述变量分别是函数Input() 和函数Middle() 的输出. 函数Middle() 通过函数Top() 建立了变量y0,y1,··· ,y17与其输出l0,l1,l2,l3之间的联系. 因此, 本节将根据第2.3.3 节所示经典实现中函数之间的关系探讨SM4 算法S 盒的量子优化实现.

首先, 对于S 盒实现中的第一层线性部分, 即函数Input(), 注意到, 其输出y0,y1,··· ,y17同时为S 盒的第一层非线性部分(函数Top()) 和第三层非线性部分(函数Bottom()) 的输入. 并且,yi(i ∈{0,1,··· ,17}) 在上述两个函数中以一定的顺序被调用. 从节约量子逻辑门数量的角度考虑, 借助18 个量子辅助比特存储y0,y1,··· ,y17有利于减少量子电路中CNOT 门的数量. 然而, 这种实现方式会增加量子电路中量子比特的开销. 因此, 本文采用一种链式的方式计算两个非线性函数所需的y0,y1,··· ,y17,将函数Input() 的实现内嵌于函数Top() 和函数Bottom() 的实现之中. 具体思路为, 按照函数Top()和函数Bottom() 调用yi的顺序, 以S 盒的输入(x0,x1,··· ,x7) 为目标比特, 依次计算yi的自更新实现, 其中i ∈{0,1,··· ,17}. 需要注意的是, 计算函数Top() 中调用的yi时,xj的初值为S 盒的输入,其中i ∈{0,1,··· ,17},j ∈{0,1,··· ,7}. 而在计算函数Bottom() 中调用的yi(i ∈{0,1,··· ,17}) 时,xj(j ∈{0,1,··· ,7}) 的初值已不再为S 盒的输入, 而是等于经过函数Top() 后被更新的值.

而对于S 盒实现中的第二层线性部分, 即函数Output(), 其输入为函数Bottom() 的输出. 如本文第2.3.3 节所示, 函数Bottom() 的各输出之间并无相互影响, 且函数Bottom() 对其输出ei(i ∈{0,1,··· ,17}) 的计算顺序没有要求, 这意味着在函数Output() 初次调用具体的ei(i ∈{0,1,··· ,17})时, 函数Bottom() 能及时提供该参数即可确保函数Output() 正确计算S 盒的输出. 而函数Output()作为线性函数, 可由F2上的二元矩阵表示, 一旦获得该矩阵的自更新实现, 即可根据该实现中最初调用ei的顺序利用函数Bottom() 计算ei, 将函数Bottom() 与函数Output() 同步实现, 最终生成S 盒的输出, 其中i ∈{0,1,··· ,17}. 因此, 本文首先设计函数Output() 的优化实现, 接着在此基础之上实现函数Bottom(), 以此将后者的实现内嵌于前者的实现之中.

根据上述分析, 本节分三步探讨SM4 算法S 盒的量子实现方案: 首先设计计算p0,p1,p2,p3的量子电路, 接着研究生成l0,l1,l2,l3的量子电路, 最后基于上述实现设计S 盒的量子实现方案.

算法1 给出了利用本文第2.3.3 节所示函数Top() 计算p0,p1,p2,p3的量子实现方案, 该方案包含了函数Input() 的实现. 算法1 对应的量子实现资源消耗为: 13 个Toffoli 门, 136 个CNOT 门以及23 个X 门, Toffoli 深度为10.

算法1 共使用5 个辅助比特, 其中4 个用于存储其输出, 即p0,p1,p2,p3(分别存储于T0,T1,T2,T3).由经典实现可知, 利用算法1 的输出基于函数Middle() 可以计算l0,l1,l2,l3, 算法2 给出了该计算过程的具体实现方案, 其对应量子实现的资源消耗为: 11 个Toffoli 门, 25 个CNOT 门以及10 个X 门, Toffoli深度为8.

算法2 共消耗9 个辅助比特, 其输出l0,l1,l2,l3分别存储于p3,T8,T6,p0, 其中T6和T8为辅助比特,p0和p3为算法1 的输出比特. 需要注意的是, 经过算法2 第9 步, 辅助比特T2被初始化为零, 在后面的实现中, 该比特可以继续作为辅助比特使用.

在生成算法2 的输出后, 即可利用经典实现中的函数Bottom() 和函数Output() 计算SM4 算法S盒的输出. 由本节的分析可知, 实现函数Bottom() 和函数Output() 的关键在于找到函数Output() 对应矩阵的自更新实现, 该矩阵如下所示:上述矩阵为行满秩矩阵, 这意味着通过添加单位向量即可将其扩展为可逆方阵, 接着利用基于矩阵分解理论的启发式算法[20]搜索其自更新实现, 继而设计函数Bottom() 的优化实现并最终实现算法S 盒.

算法1 利用5 个辅助比特计算p0,p1,p2,p3 Input: S 盒的输入(x0,x1,··· ,x7); 量子辅助比特Ti = 0,i = 0,1,··· ,4.Output: T0 = p0,T1 = p1,T2 = p2,T3 = p3, T4 待重置; xi = xi,i ∈{0,1,··· ,7}.1 x4 = x4 ⊕x2 ⊕x7;2 x6 = x6 ⊕x2 ⊕x7;3 x7 =x7;x2 ⊕x6;31 x3 = x3 ⊕x0 ⊕x6 ⊕x7;32 x1 = x1 ⊕x5 ⊕x6;33 x5 =30 x2 =T0 ⊕(x4 ·x7);5 x7 =x7;4 T0 =6 x2 = x2 ⊕x0 ⊕x3;7 T3 =x5 ⊕x3 ⊕x4;34 T2 = T2 ⊕(x2 ·x3);35 x2 =T3 ⊕(x2 ·x6);8 x2 = x2 ⊕x0 ⊕x3;9 x6 = x6 ⊕x2 ⊕x7;10 x3 =x2 ⊕x6;36 T0 = T0 ⊕T1 ⊕T3 ⊕T4;37 T1 = T1 ⊕(x1 ·x5)⊕x1 ⊕x5;38 x5 =x3 ⊕x4 ⊕x5 ⊕x7;11 x4 = x4 ⊕x6;12 T1 =x5 ⊕x3 ⊕x4;39 x3 = x3 ⊕x0 ⊕x6 ⊕x7;40 x2 =T1 ⊕(x3 ·x4);13 x3 = x3 ⊕x0 ⊕x2 ⊕x4 ⊕x7;14 x1 =x1 ⊕x3;15 T2 = T2 ⊕(x1 ·x3);16 x1 =x1 ⊕x3;17 x3 =x2 ⊕x0 ⊕x6;41 x1 = x1 ⊕x6;42 T1 = T1 ⊕(x1 ·x2);43 x1 = x1 ⊕x5;44 x2 = x2 ⊕x0;45 T1 =x3 ⊕x0 ⊕x2 ⊕x5 ⊕x6;18 x4 = x4 ⊕x2 ⊕x6 ⊕x7;19 x0 = x0 ⊕x4 ⊕x6;20 x5 = x5 ⊕x0 ⊕x1 ⊕x3 ⊕x6 ⊕x7;21 T4 =T1 ⊕T2 ⊕T3 ⊕x3 ⊕x5 ⊕x6 ⊕x7;46 T3 = T3 ⊕T2 ⊕T4;47 x7 = x7 ⊕x0 ⊕x3 ⊕x6;48 T2 = T2 ⊕(x2 ·x7);49 x2 =T4 ⊕(x0 ·x5)⊕x0 ⊕x5;22 x5 = x5 ⊕x0 ⊕x1 ⊕x2 ⊕x4 ⊕x6;23 T0 = T0 ⊕(x5 ·x6)⊕x5 ⊕x6;24 x6 =x2 ⊕x6;50 x0 = x0 ⊕x4 ⊕x6;51 x7 = x7 ⊕x0 ⊕x2 ⊕x5;52 x2 =x6 ⊕x0 ⊕x2 ⊕x5;25 x7 =x7 ⊕x0 ⊕x1 ⊕x3 ⊕x4 ⊕x6;26 T0 = T0 ⊕(x6 ·x7);27 x7 =x7 ⊕x0 ⊕x1 ⊕x3 ⊕x4 ⊕x6;28 x6 =x6 ⊕x0 ⊕x2 ⊕x5;29 x5 = x5 ⊕x2 ⊕x3 ⊕x4 ⊕x7;x2 ⊕x0 ⊕x4 ⊕x7;53 x5 = x5 ⊕x1 ⊕x6;54 T4 = T4 ⊕T0 ⊕x1 ⊕(x2 ·x5);55 T2 = T2 ⊕T4 ⊕(x6 ·x7)⊕x6 ⊕x7;56 x5 = x5 ⊕x1 ⊕x6;57 x2 =x2 ⊕x0 ⊕x4 ⊕x7;58 x7 = x7 ⊕x2 ⊕x3 ⊕x4 ⊕x5;

?算法2 利用9 个辅助比特计算l0,l1,l2,l3 Input: 算法1 的输出p0,p1,p2,p3; 量子辅助比特Ti = 0,i = 0,1,··· ,8.Output: Ti 待重置, 其中i = 0,1,3,4,5,7; T2 = 0,p3 = l0,T8 = l1,T6 = l2,p0 = l3.1 T0 =T0 ⊕(p0 ·p3);2 T1 =T4 ⊕(p2 ·T2);9 T2 =8 T4 =T1 ⊕(T0 ·p1)⊕T0 ⊕p1;3 T0 = T0 ⊕T1 ⊕p1;4 T2 =T2 ⊕p2 ⊕(p1 ·p3);5 T5 =T2 ⊕p2 ⊕(p1 ·p3);10 T3 = T3 ⊕T5;11 T6 =T5 ⊕(p0 ·T2)⊕p0 ⊕T2;6 T7 =T6 ⊕(T0 ·T3);12 p0 =T7 ⊕(T1 ·T5)⊕T1 ⊕T5;7 T3 = T3 ⊕(p1 ·T2)⊕p1 ⊕T2;p0 ⊕T3;13 T8 =T8 ⊕(T4 ·T7);14 p3 = p3 ⊕(T7 ·p2);

接下来介绍S 盒的实现方案|x〉|b〉|014〉 →|x〉|b ⊕S(x)〉|014〉. 为了减少量子比特开销, 本节采用文献[10] 中的方法, 将两个量子比特经过Toffoli 门后的状态保存于新引入的量子比特Z中, 并将之借助CNOT 门异或到所有需要Z中存储值的S 盒相应比特之中, 接着将Z的值置零用于保存下一组中间值,具体实现如算法3 所示.

算法3 需调用两次算法1 和算法2, 并且算法3 需额外借助1 个辅助比特Z. 通过初始化算法2 中的辅助比特T2(对应算法2 中第9 步) 并将之作为Z输入算法3 即可计算S 盒的输出. 该实现方案共使用14个量子辅助比特, 消耗510 个CNOT 门, 82 个Toffoli 门, 87 个X 门, Toffoli 深度为68.

4 SM4 算法的量子实现

本节介绍本文针对SM4 算法密钥扩展算法和轮函数设计的优化实现方案.

4.1 SM4 算法密钥扩展算法的量子实现

根据公式(3)可知, SM4 算法轮子密钥具体由下列方式生成:

根据密钥扩展算法的更新方式, 图3 所示电路a 给出了生成轮子密钥rki的量子实现方案. 在经过τ变换时, 该实现方案对于每一个S 盒均需引入8 个量子比特存储其输出. 因此, 假设并行处理4 个S 盒,图3 所示电路a 需使用14×4+32×5=216 个量子比特计算rki. 值得注意的是, 为了节约量子比特, 在生成当前轮轮子密钥rki后, 32 个量子辅助比特需重置, 即对L′变换后的状态经过逆T′变换, 这使得电路消耗的Toffoli 门数量和Toffoli 深度翻倍.

对公式(4)的进一步研究我们可以发现, 当前轮子密钥只与紧随其后的四轮轮子密钥的生成有关. 以K4为例,K5,K6,K7,K8的生成均与K4有关. 从K9开始, 轮子密钥的生成便与K4无关, 这意味着可以将保存K4的量子比特用于生成或保存其他轮子密钥. 同时, 由K8的生成方式可知, 置换T′的输出值直接异或到K4用于生成第5 轮轮子密钥. 因此, SM4 算法所有轮子密钥均可以不借助其他存储比特在保存种子密钥的128 个量子比特上进行更新获得.

算法3 计算输出比特初始值不受限时的S 盒Input: 经过算法1 自更新后的xi,i = 0,1,··· ,7; 算法2 的输出l0,l1,l2,l3; 量子辅助比特Z = 0.Output: s0,s1,s2,s3,s4,s5,s6,s7.1 x2 =x2 ⊕x3 ⊕x4 ⊕x5;2 Z =Z ⊕(x2 ·l2);3 s2 = s2 ⊕Z;4 s5 = s5 ⊕Z;5 s7 = s7 ⊕Z;6 Z =95 s4 = s4 ⊕Z;96 s6 = s6 ⊕Z;97 Z = Z ⊕(x1 ·l2);98 x1 =x1 ⊕x0;99 x0 =Z ⊕(x2 ·l2);7 x2 =x2 ⊕x3 ⊕x4 ⊕x5;8 x4 = x4 ⊕x2 ⊕x6 ⊕x7;9 Z = Z ⊕(x4 ·l2);10 s0 = s0 ⊕Z;11 s1 = s1 ⊕Z;12 s3 = s3 ⊕Z;13 s4 =48 Z = Z ⊕(x7 ·l0);49 s1 = s1 ⊕Z;50 s2 = s2 ⊕Z;51 s5 = s5 ⊕Z;52 s6 = s6 ⊕Z;53 Z = Z ⊕(x7 ·l0);54 x7 = x7 ⊕x0 ⊕x3 ⊕x4;55 x6 =s4 ⊕Z;14 s6 = s6 ⊕Z;15 s7 = s7 ⊕Z;16 Z = Z ⊕(x4 ·l2);17 x4 = x4 ⊕x2 ⊕x6 ⊕x7;18 x0 = x0⊕x1⊕x3⊕x4⊕x5⊕x7;19 Z =x6 ⊕x2;56 Z = Z ⊕(x6 ·l0);57 s1 = s1 ⊕Z;58 s3 = s3 ⊕Z;59 s6 = s6 ⊕Z;60 s7 = s7 ⊕Z;61 Z = Z ⊕(x6 ·l0);62 x6 =x6 ⊕x2;63 l0 = l0 ⊕l1;64 x0 = x0 ⊕x2 ⊕x3;65 s0 =x0⊕x2⊕x3⊕x5⊕x6;100 l2 = l2 ⊕l1 ⊕l0;101 x5 = x5 ⊕x1 ⊕x6;102 Z = Z ⊕(x5 ·l2);103 s1 = s1 ⊕Z;104 s2 = s2 ⊕Z;105 s3 = s3 ⊕Z;106 s5 = s5 ⊕Z;107 s6 = s6 ⊕Z;108 s7 = s7 ⊕Z;109 Z = Z ⊕(x5 ·l2);110 x5 = x5 ⊕x1 ⊕x6;111 x3 =Z ⊕(x0 ·l3);20 s3 = s3 ⊕Z;21 s7 = s7 ⊕Z;22 Z = Z ⊕(x0 ·l3);23 x0 = x0⊕x1⊕x3⊕x4⊕x5⊕x7;24 x6 = x6 ⊕x0 ⊕x4;25 Z = Z ⊕(x6 ·l3);26 s1 = s1 ⊕Z;27 s2 = s2 ⊕Z;28 Z = Z ⊕(x6 ·l3);29 x6 = x6 ⊕x0 ⊕x4;30 x7 =x7;x3 ⊕x0 ⊕x5 ⊕x7;112 Z = Z ⊕(x3 ·l2);113 s2 = s2 ⊕Z;114 s3 = s3 ⊕Z;115 s6 = s6 ⊕Z;116 s7 = s7 ⊕Z;117 Z = Z ⊕(x3 ·l2);118 x3 =31 Z = Z ⊕(x7 ·l1);32 s1 = s1 ⊕Z;33 s3 = s3 ⊕Z;34 s5 = s5 ⊕Z;35 s6 = s6 ⊕Z;36 Z = Z ⊕(x7 ·l1);37 x7 =x7;s0 ⊕(x0 ·l0);66 x0 = x0 ⊕x2 ⊕x3;67 x2 = x2 ⊕x6 ⊕x7;68 Z = Z ⊕(x2 ·l0);69 s5 = s5 ⊕Z;70 s7 = s7 ⊕Z;71 Z = Z ⊕(x2 ·l0);72 x2 = x2 ⊕x6 ⊕x7;73 l0 = l0 ⊕l1;74 l1 = l1 ⊕l2;75 Z = Z ⊕(x6 ·l1);76 s1 = s1 ⊕Z;77 s4 = s4 ⊕Z;78 s6 = s6 ⊕Z;79 Z = Z ⊕(x6 ·l1);80 x5 = x5 ⊕x2 ⊕x3 ⊕x4 ⊕x7;81 s1 =x3 ⊕x0 ⊕x5 ⊕x7;119 l2 = l2 ⊕l3 ⊕l1 ⊕l0;120 l3 = l3 ⊕l0;121 x1 = x1 ⊕x5;122 Z = Z ⊕(x1 ·l3);123 s2 = s2 ⊕Z;124 s3 = s3 ⊕Z;125 s4 = s4 ⊕Z;126 s5 = s5 ⊕Z;127 s7 = s7 ⊕Z;128 Z = Z ⊕(x1 ·l3);129 x1 = x1 ⊕x5;130 x0 =38 x2 = x2 ⊕x4 ⊕x7;39 Z = Z ⊕(x2 ·l1);40 s0 = s0 ⊕Z;41 s1 = s1 ⊕Z;42 s2 = s2 ⊕Z;43 s5 = s5 ⊕Z;44 s6 = s6 ⊕Z;45 Z = Z ⊕(x2 ·l1);46 x2 = x2 ⊕x4 ⊕x7;47 x7 = x7 ⊕x0 ⊕x3 ⊕x4;s1 ⊕(x5 ·l1);82 x5 = x5 ⊕x2 ⊕x3 ⊕x4 ⊕x7;83 l1 = l1 ⊕l2;84 l2 = l2 ⊕l3;85 x0 =x0 ⊕x2 ⊕x3 ⊕x5 ⊕x6;86 Z = Z ⊕(x0 ·l2);87 s1 = s1 ⊕Z;88 s5 = s5 ⊕Z;89 s7 = s7 ⊕Z;90 Z = Z ⊕(x0 ·l2);91 x1 =x0 ⊕x2 ⊕x4;131 Z = Z ⊕(x0 ·l3);132 s1 = s1 ⊕Z;133 s2 = s2 ⊕Z;134 s3 = s3 ⊕Z;135 s6 = s6 ⊕Z;136 s7 = s7 ⊕Z;137 Z =x1 ⊕x0;92 Z = Z ⊕(x1 ·l2);93 s0 = s0 ⊕Z;94 s1 = s1 ⊕Z;Z ⊕(x0 ·l3);138 x0 =x0 ⊕x2 ⊕x4;139 l3 = l3 ⊕l0;140 运行算法1–2 重置辅助比特;

图3 轮子密钥rki 的生成Figure 3 Generation of subkey rki

下面介绍一种优化的生成轮子密钥rki的量子电路结构, 如图3 电路b 所示实现方案.

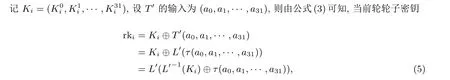
其中L′-1为L′的逆变换.

根据上述分析, 同时考虑到轮子密钥的特殊性(一方面, 轮子密钥需输入算法轮函数用于更新状态; 另一方面, 作为计算下一轮轮子密钥的参数其值需继续保留.), 本节利用算法3 设计了如图4 所示SM4 算法密钥扩展算法的量子实现方案.

值得注意的是, 图4 并未显示实现S 盒所需的量子辅助比特. 同时, 将给定参数异或到状态位中, 等价于将状态位中与固定参数中值为1 的比特对应的比特位取反. SM4 算法的给定参数中, 轮常量的汉明重量为503, 系统参数的汉明重量为64, 即使用503+64 = 567 个X 门即可完成异或轮常数和系统参数.图4 所示SM4 算法密钥扩展算法量子实现的资源开销分析如下:

图4 共消耗128 个基于32 比特的异或, 32 个τ变换, 每一个τ变换包含4 个S 盒. 此外, 该实现使用32 次逆线性变换, 由于量子电路要求可逆, 线性变换及其逆变换的量子实现代价相等. 考虑到量子比特数和电路深度对指标depth-times-width 值的影响, S 盒又是影响量子电路所需量子辅助比特和电路深度的主要组件, 因此τ变换中S 盒的实现方式直接关系着量子电路的整体表现. 综上所述, 假设一次τ变换中, 并行处理的S 盒数量为i(i ∈{1,2,4}), 图4 所示实现方案共需要128+14×i个量子比特,(82×4)×32 = 10496 个Toffoli 门, (510×4)×32+128×32+78×2×32 = 74368 个CNOT 门,87×4×32+1070=12206 个X 门, Toffoli 深度为(68×(4/i))×32, 其中i ∈{1,2,4}.

图4 SM4 算法密钥扩展算法的实现Figure 4 Implementation of key expansion of SM4

4.2 SM4 算法整体实现结构

由公式(2)可知, SM4 算法轮函数的展开与其密钥扩展算法类似, 因此, 本文利用算法3 设计了如图5 所示SM4 算法轮函数的实现方案.

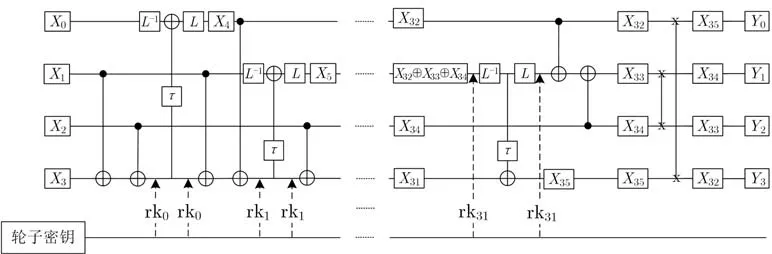
图5 SM4 算法轮函数的实现Figure 5 Implementation of round function of SM4

利用图5 所示结构更新SM4 算法轮函数的量子资源开销分析如下:

基于图4 的输出, 即算法轮子密钥已知的情形下, 图5 共消耗基于32 比特的异或150 个, 其中32 个用于异或轮子密钥, 86 个用于更新状态, 32 个用于消除状态位中被异或的轮子密钥以便进行下一轮状态更新. 电路还消耗32 个τ变换, 每一个τ变换包含4 个S 盒. 此外, 算法反序函数共需要64 次基于比特的SWAP 操作, 可由64×3 = 192 个CNOT 门模拟. 与密钥扩展算法量子实现方案的分析类似, 假设一次τ变换中, 并行处理的S 盒数量为i(i ∈{1,2,4}), 图5 所示实现方案共需要128+14×i个量子比特, (82×4)×32 = 10496 个Toffoli 门, (510×4)×32+150×32+83×2×32+192 = 75584 个CNOT 门, 87×4×32=11136 个X 门, Toffoli 深度为(68×(4/i))×32, 其中i ∈{1,2,4}.

考虑到密钥扩展算法与算法轮函数之间的关系, 本文结合图4 和图5 设计了SM4 算法量子实现整体结构, 如图6 所示.

图6 SM4 算法整体加密结构Figure 6 Whole encrypt sctructure of SM4

图6 中的虚线将SM4 算法的整体量子实现分为三个部分: 第一部分更新密钥, 生成rk0(K4). 该部分电路仅经过一次τ变换, 即包含4 个S 盒; 第二部分更新密钥和轮函数. 该部分电路计算算法第i轮的输出以及算法第i+1 轮的轮子密钥, 其中i=1,2,··· ,31. 因此, 图6 所示电路第二部分每一次更新经过两个τ变换(如图6 中虚线框所示), 即包含8 个S 盒; 第三部分生成密文. 此时电路仅经过一次τ变换, 即包含4 个S 盒.

由表2 中的结果可知, 采用本文设计的如图6 所示SM4 算法的量子实现整体结构, 随着i的取值变大, 即电路并行处理的S 盒数量增加, 电路所需量子比特数增加, 电路的depth-times-width 值减小. 与AES-128 的量子实现相比, 本文针对SM4 算法设计的量子实现整体结构使用的量子比特数明显减少. 这是由于, 一方面, 直接将针对AES 设计的zig-zag 结构运用于基于Feistel 结构的密码算法并不一定是最优选择; 另一方面, 利用本文提出的算法3 对SM4 算法合成置换T和T′的改进实现, 进一步减少了量子电路中量子比特的使用数量.

5 SM4 算法量子穷举攻击

本节基于如图6 所示整体实现结构评估利用Grover 算法搜索SM4 算法密钥的量子资源开销.

表2 SM4 算法与AES-128 算法实现开销对比Table 2 Comparison of cost to implement SM4 and AES-128

(1) 制备均匀叠加态以及|-〉所需的Hadamard 门;

(a)Uf的开销;

(b) 相位翻转的开销, 即实现2|0〉〈0|-1 的代价;

(c) 相位翻转前后所需的Hadamard 门.

针对分组长度为128 比特的分组密码，借助两对明密文对即可确定128 比特密钥的唯一值，因此，利用Grover 算法对密钥长度为128 比特的分组密码进行量子穷举攻击时所使用的量子电路Uf通常如图7 所示, 其中Enc 为密码算法的可逆量子电路, Enc-1为其逆电路.

图7 函数Uf 对应的可逆实现Figure 7 Reversible implementation of Uf

图7 所示量子电路中, 两个“Enc” 并行运行, 两个“Enc-1” 并行运行, 电路Toffoli 深度翻倍. 同时,文献[6] 指出, 根据文献[21] 的研究, 给定两组明密文对, 经过密码算法可逆电路之后判断输出值与密文是否相等需使用8·(128·2)-24 个Toffoli 门. 而对于相位翻转, 参考文献[6] 指出, 实现2|0〉〈0|-1 的量子资源开销为8·128-24 个Toffoli 门. 综上, 结合图1和图7 所示电路对分组长度和密钥长度均为128比特的分组密码进行量子穷举攻击的代价分析如下:

Toffoli 门的数量为

其中ΔToffoli为密码算法的量子实现电路中消耗的Toffoli 门数.

CNOT 门的数量为

其中ΔCNOT为密码算法的量子实现电路中消耗的CNOT 门数.

X门的数量为

其中ΔX为密码算法的量子实现电路中消耗的X 门数.

Hadamard 门的数量为

电路Toffoli 深度可参照文献[6] 近似为

其中ΔDepth为密码算法量子实现电路的Toffoli 深度.

电路所需量子比特数为

其中Δqubit为密码算法量子实现电路所需量子比特总数.

SM4 算法与AES-128 均为分组长度和密钥长度等于128 比特的分组密码, 将表2 所示算法的量子实现开销代入公式(6)—(11)即可计算利用Grover 算法搜索SM4 算法和AES-128 算法密钥的量子资源开销, 具体如表3 所示.

表3 SM4 算法与AES-128 算法的量子穷举攻击开销对比Table 3 Comparison of cost to conduct quantum exhaustive key search for SM4 and AES-128

一方面, 针对密码算法的抗量子攻击安全强度, NIST 定义了五种类别, 分别与对五种经典密码算法进行量子穷举攻击所需计算资源有关[2]. 以第一类为例, 满足第一等级安全强度的密码算法, 对其进行任意攻击的计算资源需与对AES-128 进行密钥穷搜的计算资源相当或比之更多. 由文献[2] 可知, 对密码算法进行量子分析所需的计算资源可以由经典环境下基本操作的数目或量子电路的大小等指标度量, 而量子电路的大小与该电路所需量子比特数有关; 另一方面, 文献[9] 指出, 量子逻辑门的消耗与NIST 定义的抗量子攻击安全类别相关,但是在考虑量子纠错的情况下,depth-times-width 值是更加实际的评估量子资源消耗的指标. 因此, 我们可以通过利用Grover 算法进行密钥穷搜的电路所消耗的量子比特数目和该电路的depth-times-width 值合理地比较SM4 算法与AES-128 算法抗量子穷举攻击的强度. 如表3 所示, 针对量子比特数量, 无论并行S 盒的数量如何, 利用本文设计的SM4 算法量子实现方案构造的量子穷举攻击所需量子比特均比对AES-128 进行密钥穷搜的量子电路所需量子比特少. 此外, 针对指标depth-timeswidth 值, 本文提出了一种并行处理S 盒数量为8 的SM4 算法量子实现方案, 利用该实现方案构造的量子穷举攻击具有比对AES-128 的量子穷举攻击更低的depth-times-width 值. 虽然比AES-128 更长的加密轮数一定程度增加了实现SM4 算法所需的量子资源, 但是从量子比特数目和depth-times-width 值两个指标出发, 本文的研究表明, SM4 算法的抗量子穷举攻击强度要弱于AES-128 算法.

6 总结

本文首先研究了SM4 算法线性层的量子实现, 不同于目前研究分组密码的量子实现时普遍采用LUP分解的方法, 本文利用基于矩阵分解理论的启发式算法生成了SM4 算法线性层异或门电路消耗更少、异或深度更小的经典实现, 该实现可通过借助CNOT 门模拟异或操作转换为量子实现; 其次, 从SM4 算法S 盒的经典实现出发, 利用基于矩阵分解理论的启发式算法实现其线性部分, 并在此基础上构造了SM4算法S 盒的量子优化实现方案, 该实现需借助14 个量子辅助比特并且对S 盒的输出比特初值没有任何限制条件; 借助本文设计的S 盒量子实现的上述性质, 同时考虑到SM4 算法的密码结构特性, 本文通过添加逆线性变换的方法构造了能有效节约32 个量子比特的T和T′的量子优化实现方案; 基于上述改进实现方案, 根据算法轮子密钥和状态更新的特点针对密钥扩展算法和轮函数分别设计了一种量子优化实现方案; 接着, 探索了适用于基于Feistel 结构密码算法的量子实现整体结构. 目前对称密码算法量子实现的研究主要集中在AES 算法上面, 为了减少量子比特开销, 学者基于AES 算法SPN 结构提出的zig-zag 结构需要计算轮函数的逆. 本文研究表明, 针对AES 算法设计的zig-zag 结构并不适用于实现基于Feistel结构的密码算法. 利用Feistel 结构轮函数输出异或到其中一个分支以及本文所设计S 盒的量子实现, 本文提出了一种具有较高灵活性、量子比特消耗比直接采用zig-zag 结构少、并且与zig-zag 结构相比无需对算法整轮求逆以节约量子比特的SM4 算法量子实现整体结构. 综合考虑电路所耗量子比特数和电路Toffoli 深度对量子电路整体性能的影响, 研究了当电路并行处理的S 盒数量分别为1、2、4、8 时SM4算法整体实现方案的量子资源开销; 最后, 基于本文设计的SM4 算法量子实现整体结构, 结合Grover 算法, 研究了对SM4 算法进行量子穷举攻击所需的量子资源开销, 并且比较了SM4 算法与AES-128 算法抵抗量子穷举攻击的安全性强度.