改进的五轮Grøstl-512 的量子碰撞攻击*

董炳佑, 刘 泰, 崔玉龙, 倪博煜, 秦岭月, 董晓阳

1. 清华大学高等研究院, 北京 100084

2. 中车青岛四方机车车辆股份有限公司, 青岛 266111

3. 山东大学密码技术与信息安全教育部重点实验室, 济南 250199

4. 山东大学网络空间安全学院, 青岛 266237

1 前言

在1994 年, Shor 算法[1]的提出, 说明一个足够大的量子计算机可以在多项式时间内分解大整数、计算离散对数问题等, 对目前使用的许多公钥密码方案都带来重大安全影响. 这激起了大家对抗量子计算机攻击的密码的研究兴趣, 公钥密码学社区和标准化组织在后量子公钥密码学的研究上投入了大量的精力.相比之下, 人们普遍认为, 量子计算攻击对对称密码安全性影响有限, 因为当攻击者使用量子计算机攻击对称密码时, 优势是使用Grover 算法[2]来加速密钥的搜索, 然而将密钥长度加倍就可以解决这个问题.直到2010 年, Kuwakado 和Morii 证明了经典可证明安全的Even-Mansour 结构密码和三轮Feistel 结构可以在量子计算机的帮助下在多项式时间内被破解[3,4]. 接下来的几年, 更多的对称密码设计结构被量子计算算法攻击[5–13]. 几乎所有这些指数级加速的攻击都是通过Simon 的算法[14]来找到一个依赖于密钥的隐藏周期, 在寻找这个隐藏周期时, 需要以量子明文叠加态访问加密算法, 并获得密文叠加态. 这是一个相当强的要求, 敌手需要在线访问一个用量子电路实现的加密算法. 因此, 如果不需要对密钥原语的量子叠加预言机进行在线查询, 那么使用更高复杂度的量子计算攻击仍然是有意义的[7,15].

与加密算法不同, 哈希函数不需要密钥. 因此敌手可以离线实现哈希函数的量子电路, 并利用量子叠加态访问该量子电路, 并获得量子叠加态. 一个安全哈希函数需要具备抗碰撞攻击、抗原象攻击和抗第二原象攻击等安全属性, 本文针对AES 类哈希函数抗碰撞攻击的安全性展开研究. AES 类哈希函数采用类似于AES 的轮函数设计, 典型AES 类哈希算法包括AES 哈希模式AES-MMO/MP、Grøstl[16]、Whirlpool[17]等. 经典计算环境下, 反弹攻击[18]是分析AES 类哈希函数的有效手段. 在量子计算环境下, Hosoyamada 和Sasaki[19]在2020 年欧密会上提出反弹攻击的量子实现算法, 给出了7 轮AESMMO 和6 轮Whirlpool[17]的量子碰撞攻击. 在2020 年亚密会上, 董晓阳等[20]提出了不使用qRAM的量子碰撞攻击, 首次超越Chailloux 等[21]给出的一般碰撞攻击界. 在2021 年美密会上, Hosoyamada和Sasaki[22]提出了一些列减轮SHA-2 算法的量子碰撞攻击. 在ToSC 2020 上, Chauhan 等[23]研究了双块AES 压缩函数模式的量子碰撞攻击. 在ToSC 2021 上, 倪博煜等[24]研究了Simpira v2 哈希模式的量子碰撞攻击. 在2021 年亚密会上, 董晓阳等[25]研究了哈希函数的自由起始的量子碰撞攻击.

对于一个输出为n比特摘要值的哈希函数, 在经典环境下, 需要O(2n/2) 的时间复杂度来寻找碰撞.在量子计算环境下, 根据已有的量子算法可以得到以下碰撞的一般界:

(3) CNS 算法[21]需要时间复杂度T=22n/5来找到一组碰撞, 另外需要大小为2n/5的经典内存.那么, 一个成功的量子碰撞攻击必须优于至少一种量子碰撞攻击一般界.

1.1 本文贡献

表1 针对Grøstl 的经典与量子碰撞攻击Table 1 Classical and quantum collision attacks on Grøstl

2 预备知识

本节简要介绍类AES 哈希函数、反弹攻击、量子计算和量子随机存储器(quantum random access memory, qRAM), 以及一些常用的量子算法.

2.1 类AES 哈希函数

为明确起见, 首先回顾AES-128 的轮函数. 它作用在排列成矩阵的16 字节状态上, 包括四个主要的变换: 字节替换SubBytes(SB)、行位移ShiftRows(SR)、列混合MixColumns(MC) 和密钥加AddRoundKey(AK), 如图1 所示. 对这些变换适当修改, 就可以改变轮函数的参数, 如矩阵的行列数量、单元的大小、变换作用的顺序, 乃至交换行列排列(亦即将矩阵转置), 进而新参数可以生成新的轮函数设计.这种在AES 轮函数上进行修改的设计可以粗略称为类AES 轮函数. 本文假定列混合(MC) 是将状态矩阵的每一列乘上一个MDS 矩阵的操作.

图1 AES 轮函数Figure 1 Round function of AES

Grøstl 算法是SHA-3 最终候选哈希函数之一, 有Grøstl-256 和Grøstl-512 两个版本. 处理两个消息分组的的结构如图2, 其中P和Q是两个n比特的类AES 置换. 在算法输出哈希值之前,一个基于P的输出变换和一个截断函数Ω :→会作用在h2上. 更多算法设计细节读者可以参考文献[16].

董晓阳等[20]给出了Grøstl-512 的4 轮、5 轮经典和量子碰撞攻击. 图3 展示了Grøstl 的等价描述.令P-和Q-为去掉最后一个MixBytes(MB) 操作的类AES 置换, 有如下等价表示, 其中1≤i ≤t,

图2 处理两个消息分组的Grøstl-Figure 2 Grøstl- with two message blocks

图3 处理两个消息分组的Grøstl-: 等价表示Figure 3 Alternative descriptionofGrøstl-n withtwomessage blocks

2.2 量子计算和量子随机存储器

一个拥有n个量子比特的系统状态可以描述为 C2n空间上的一个单位向量, 可取一组正交基{|0···00〉,|0···01〉,··· ,|1···11〉}来表示, 称为计算基(computational basis). 它是量子计算中常用的一组基, 亦可记为{|i〉: 0≤i ＜2n}. 一般来说, 量子算法的实现即是利用一系列的酉变换和测量对量子系统进行操控, 而所有的酉变换可以用一组单量子比特和双量子比特变换来表示. 这种表示即是标准量子电路模型下的量子门表示, 一个量子算法的效率就可以用表示该算法需要使用的量子门数量来定量描述.

2.2.1 经典电路的叠加态预言机

给定一个经典的布尔函数:f:→F2.f的叠加态预言机定义为作用在一个(n+1)-量子比特的系统上的酉变换Uf, 它将基态|x,y〉变为|x,y ⊕f(x)〉, 其中x ∈,y ∈F2. 作为一个线性算子,Uf作用在叠加态上将得到

注意到, 只要存在一个高效的经典电路可以计算f, 那么Uf就可以用量子电路模型高效实现, 而如前所述, 这只需要找到一个实现f的高效可逆电路, 再将其中的可逆门电路用量子门替代就可以了.

2.2.2 Grover 算法[2]

这里存在一个漏洞: Grover 算法的整体复杂性可能被隐藏在所调用的预言机电路的构造开销中了.除非预言机的电路可以被高效实现, 否则算法对于搜索的加速将会没有作用. 因此, 明确实现这样的预言机需要怎样的资源是十分重要的, 例如高效实现预言机可能需要一个大容量的qRAM.

2.2.3 量子振幅放大算法[31]

量子振幅放大可以视作Grover 算法的一种推广, 后者限制A产生所有基向量的均一叠加态. 类似地, 在分析量子振幅放大的复杂度时, 应当计入实现UP和A的复杂度.

2.2.4 量子随机存储器(qRAM)

量子随机存储器(qRAM) 是经典随机存储器(RAM) 的量子版本, 它使用n量子比特来表示任何2n个存储单元构成的量子叠加态. 给定一列经典数据L={x0,x1,··· ,x2n-1}, 其中xi ∈Fm2,L对应的qRAM 可以用一个酉变换

其中i ∈,y ∈, 且|·〉Addr和|·〉Out分别是地址和输出存储器. 这样一来, 就可以访问这些数据的任意量子叠加态, 输入对应地址的量子叠加态就能得到:

到目前为止, 如何构造一个可行的qRAM (至少说是大容量的qRAM) 仍旧未知. 尽管如此, 这一令人失望的事实并没有阻止研究者在假定大容量qRAM 可用的模型下开展工作, 就像人们在经典或量子计算机被建造出来之前早就开始研究经典或量子算法一样. 另一方面, 大容量qRAM 尚未出现, 而规模O(n) 的qRAM 可以用规模O(n) 的量子电路进行模拟, 因此尝试减少甚至避免qRAM 在量子算法中的使用进行研究是相当有意义的.

2.3 反弹攻击及其改进

反弹攻击是由文献[18] 首先引入的, 如图4 所示, 它包含入站阶段(Inbound) 和出站阶段(Outbound). 在入站阶段, 通过中间相遇降低复杂度, 从而找到满足入站阶段差分的数据对, 该数据对被称为起点(Starting Point). 然后在出站阶段, 通过大量的起点数据对分别向前和向后推算, 找到满足出站阶段差分的数据对.

图4 反弹攻击Figure 4 Rebound attack

为了提升入站阶段的差分路径可以覆盖的轮数, 文献[32,33] 分别独立地提出了超级S 盒技术, 把连续两轮类AES 轮函数视作一个由超级S 盒构成的整体. 后来文献[34] 指出利用非全活跃超级S 盒的差分性质可以显著地降低反弹攻击所需要的空间复杂度.

下面考虑更一般的情况: 某密码系统的内部状态是一个d×d矩阵, 每个单元代表c比特数据. 参考图5 是d=4 的情况, 对应有d=4 个超级S 盒.

2.4 全活跃超级S 盒

沿用图5 中的记号, 利用全活跃超级S 盒的反弹攻击的入站阶段, 步骤如下:

图5 全活跃与非全活跃超级S 盒差分路径对比Figure 5 Differential of full-active and non-full-active super S-box

对于给定的Δin, 可以生成2d·c对起点, 需要d×2d·c的空间来储存d个列表, 生成一对起点的平均时间复杂度为O(1).

2.5 非全活跃超级S 盒

考虑一列由d个c比特单元组成的状态A, 经过超级S 盒SSB = SB°MC°SB 被映射为状态D= SSB(A), 中间状态依次为B和C, 其中SB 是d个c×c的小S 盒的并联, 而MC : Fd2c →Fd2c是分支数为n+1 的MDS 线性变换, 那么有命题1 成立.

命题1(MDS 性质) 令MC·(X[0],X[1],··· ,X[d-1])T= (Y[0],Y[1],··· ,Y[d-1])T, 若X[0],X[1],··· ,X[d-1],Y[0],Y[1],··· ,Y[d-1] 中至少一半已知, 那么可以由等式关系推知其余未知项.

假设一个差分输入超级S 盒, 使得其中有s个c×c的S 盒不活跃, 那么活跃的S 盒有2d-s个. 而S 盒不会改变作用前后状态中各单元的差分, 所以(A,D) 和(B,C) 都各有s个单元不活跃. 为了生成一对数据, 使其满足给定的输入输出差分(ΔA,ΔD), 进行以下操作:

(1) 猜测(A,D) 的活跃单元中的d-s个单元.

(2) 由(A,D) 猜测的d-s个单元计算(B,C) 中对应的d-s个单元, 并计算差分(ΔB,ΔC).

(3) 结合(ΔB,ΔC) 中s个不活跃的单元差分, 共有d单元被MC 作用的输入输出差分已知. 根据命题1, 可以求得这一截断差分路径中的所有差分.

(4) 现在(B,C) 中d-s个单元已被确定, 另需确定s个单元才能通过MC 完全确定(B,C) 的全部单元. 通过查询DDTs次来获得这s个单元, 引入s比特辅助变量β来区分2s种可能的选择.

(5) 结合步骤(2) 获得(B,C) 的d-s个单元和由DDT 获得的s个单元, 根据命题1 可以确定余下的d个单元.

(6) 至此, 剩余未用的活跃S 盒数目为

可以当做一个(d-s)c比特的筛选器, 满足差分的过筛概率为2-(d-s)c. 这样就得到了满足给定SSB 差分的完整数据对(A,D) 和(A′,D′).

上述操作的复杂度包含s次DDT 查询和4(d-s) 次S 盒计算. 平均意义上, 成功找到一对数据需要重复操作2(d-s)c×2s次以遍历初始猜测和s比特辅助变量β, 对应大约2(d-s)c+s×s次DDT 查询和2(d-s)c+s×4(d-s) 次S 盒计算. 假设一次DDT 查询相当于一次S 盒计算, 那么经典设定下的整体时间复杂度为:

而在量子设定下, 利用Grover 算法得到加速后的时间复杂度(包括逆运算) 为:

同时需要216大小的qRAM 来存储DDT. 详细定义及实现参见文献[20].

根据式公式(1) 与(2), 复杂度主项为2(d-s)c(在本文中c=8), 因此最大化s可以降低复杂度.

3 董晓阳等的5 轮Grøstl-512 的碰撞攻击[20]

3.1 5 轮经典碰撞攻击

(1) 随机选取240对消息分组(m0,m′0), 计算差分Δv1=v1⊕v′1, 使得蓝色字节对应的差分满足初始条件, 平均而言可以得到一组满足条件的(m0,m′0) 和Δv1.

(2) 针对消息分组m1进行反弹攻击. 注意到输入差分Δin由Δv1唯一确定, 而输出差分Δout有8个活跃字节, 因此利用全活跃超级S 盒技术, 可以找到264个m1满足对应的入站阶段的差分路径. 而对于出站阶段的差分路径, 后向的截断差分路径(128→64→8→1→8→8) 成立的概率为2-56, 而前向的差分传播经过一次前馈8 字节异或, 差分抵消的概率为2-64. 因此可以以概率264×2-56×2-64=2-56确定满足要求的差分路径和中间状态v2, 对应的时间复杂度为264.如果没有求得所需差分, 那么用下一个消息分组和之前产生的中间状态来重复同样的攻击. 平均而言, 在对256个消息分组进行计算之后会成功消去差分, 得到正确的路径.

(3) 重复步骤(2), 不断逐列消去中间状态包含的活跃差分, 直到剩余两列活跃差分.

(4) 可以利用步骤(2) 的技巧同时消去最后两列活跃差分, 但反弹攻击的成功概率有所不同. 因为入站阶段的差分的输出状态中有16 个活跃字节, 可以利用全活跃超级S 盒技术得到216×8= 2128个起点, 对应的时间复杂度为2128. 接着考虑出站阶段的差分, 相应的截断差分路径(88→96→16→2→16→16) 成立的概率为2-112, 而两列之间的相互消去发生的概率为2-128. 因此在步骤(4) 之内, 有2128×2-112×2-128=2-112的概率得到满足要求的碰撞, 对应的时间复杂度为2128. 同样地, 在平均意义上用2112个消息分组重复步骤(4) 就能得到碰撞.

上述攻击的时间复杂度主项是步骤(4), 可以估计为2112×2128=2240. 存储超级S 盒需要空间复杂度264. 最终, 获得一组碰撞使用了2112个消息分组计算.

3.2 5 轮Grøstl-512 量子碰撞攻击

董晓阳等[20]中基于上述5 轮经典碰撞攻击, 利用量子算法可以得到加速后的5 轮量子碰撞攻击, 即用Grover 算法替代经典攻击中的穷举搜索.

图6 5 轮Grostl-512 的碰撞攻击Figure 6 Collision attacks on 5-round Grostl-512

(1) 利用Grover 算法,找到符合蓝色字节的初始条件的第一轮输入一对消息分组和对应输出差分,所对应的复杂度约是经典情况的一半规模, 即220.

(2) 逐列消去中间状态差分的多轮反弹攻击, 每一轮都需要检查264对起点(Δin,Δout) 是否能推导出8 个活跃字节的消除. 这里整个状态空间大小为264, SB 操作涉及16 个独立联合作用的超级S 盒, 利用2.5 节的技术, 需要增加15 比特的辅助变量α, 因而搜索空间扩大到264×215=279.

(3) 最后一轮反弹攻击同时消去两列差分, 与步骤(2) 相似, 也需要15 比特的辅助变量α, 搜索空间相应地扩大到2128×215轮Grøstl-512 中有5×2×128 = 1280 次S 盒计算, 这里与文献[20] 中用4 轮Grøstl-512 来估计不同., 这一部分是复杂性的主项.

相当于226.67/1280≈216.35次5 轮Grøstl-512 运算. 类似的,s=4 的SSB 有6 个, 每个对应的时间复杂度约为212.65次5 轮Grøstl-512 运算, 而s ≥5 的SSB 对应的时间复杂度可以忽略不计. 综上, 步骤(3) 的时间复杂度为

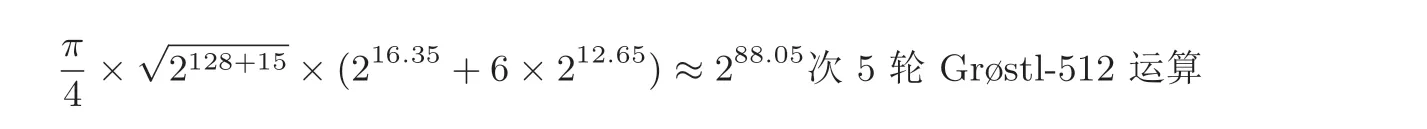
图7 五轮Grøstl-512 的碰撞攻击中的最后一轮反弹攻击差分路径示意图[20]Figure 7 Inbound phase of last step of collision attack on Grøstl-512 [20]

平均意义上, 成功找到一组碰撞需要运行14 轮步骤(2), 每轮重复256次, 还需要将步骤(3) 重复运行2112次, 前者相对后者可以忽略不计. 因此量子碰撞攻击的时间复杂度为288.05×2112≈2200.05, 同时需要216大小的qRAM 来储存DDT.

类似地, 为了成功找到一组碰撞平均需要将步骤(3) 重复运行2112次, 因此不需要qRAM 的量子碰撞攻击总的时间复杂度为289.00×2112≈2201.0.

因为使用5 轮Grøstl-512 (1280 个S 盒) 而非4 轮Grøstl-512 (1024 个S 盒) 来估计时间复杂度,这里给出的复杂度结论与文献[20] 中略有不同, 总体上少了大约1280/1024≈20.32.

4 改进的5 轮Grøstl-512 量子碰撞攻击

4.1 基本算法实现细节

为了明确使用振幅放大算法进行碰撞攻击的细节, 首先推导文献[20] 中Grøstl-512 碰撞攻击的实现细节, 这部分在文献[20] 作为利用非全活跃超级S 盒的AES-MMO 碰撞攻击的推广没有明确给出.

首先, 需要预先计算DDT 的输入输出差分, 存储在表中以便查询, 即文献[20] 中的算法1.

算法1 S 盒S(x) 的输入输出差分分布表[20]Output: T 1 Let T be an empty dictionary;2 for δin ∈F82 do 3for x ∈F82 do 4 x′ ←x ⊕δin, y ←S(x), y′ ←S(x′), δout ←y ⊕y′;5 if x ≤x′ then 6 Insert (x,x′,y,y′) into T[(δin,δout)];end 8end 9 end 10 return T;7

接下来着重分析反弹攻击最后一轮中用到的非全活跃超级S 盒的差分路径, 因为这一轮是整个碰撞攻击过程中复杂性的主项. 以图7 中红框标出的一个超级S 盒为例, 其不活跃字节数s=7, 截断差分路径如图8. 从这个例子出发, 整个攻击中涉及的其他超级S 盒的差分路径可以结合2.5 节的结论进行类推.

图8 Grøstl-512 最后一轮反弹攻击中一个非全活跃超级S 盒的截断差分路径Figure 8 Differential of one non-full-active super S-box in last round rebound attack of Grøstl-512

根据2.5 节的一般化讨论, 取Grøstl-512 对应的参数为d=8,c=8, 则可利用命题1 生成满足该SSB的差分路径的数据对, 具体步骤如算法2 所示. 这需要先猜测d-s= 1 个(A,D) 中的活跃字节(不妨设为A[0]), 作为输入传递给算法2 最终输出所需数据对. 算法2 的成功概率为2-7×2-8=2-15, 因此在平均意义下遍历15 比特输入(A[0],β) 后可以输出1 对满足SSB 输入输出差分的数据对. 算法2 运行一次需要执行s= 7 次DDT 访问(步骤3 到9) 和4 次S 盒计算(步骤1 和25), 因此输出所需数据对的平均复杂度为215×11, 这符合将d=8,c=8,s=7 代入公式(1)的结果.

算法2 生成非全活跃超级S 盒的输入输出数据对Input: (ΔA,ΔD), A[0], β = (β0,··· ,β7)Output: 数据A 满足SSB(A)⊕SSB(A ⊕ΔA) = ΔD 1 B[0] = S(A[0]), B′[0] = S(A[0]⊕ΔA[0]), ΔB[0] = B[0]⊕B′[0]/* 算上(ΔB,ΔC) 中7 个非活跃字节, 总计2 利用命题1, 计算ΔB[1],ΔB[2],ΔB[5],ΔB[7] 和ΔC[1],ΔC[3],ΔC[5],ΔC[7]/* 查询DDT 获取对应输入输出差分的数据,3 (A[2],A′[2],B[2],B′[2]) ←T[(ΔA[2],ΔB[2])]4 for i ∈{3,5,7} do 5(A[i],A′[i],B[i],B′[i]) ←T[(ΔA[i],ΔB[i])]6(C[i],C′[i],D[i],D′[i]) ←T[(ΔC[i],ΔD[i])]7 end/* 按β 的值选取(A[2],A[3],A[5],A[7],C[3],C[5],C[7]) 的组合: 若β0 = 0 则取β0 = 1 则取β0 ·ΔA[2] = ΔA[2] */8 A[2] = A[2]⊕β0 ·ΔA[2], A′[2] = A[2]⊕ΔA[2];9 B[2] = B[2]⊕β0 ·ΔB[2], B′[2] = B[2]⊕ΔB[2];10 for (i,j) ∈{(3,1),(5,2),(7,3)} do 11A[i] = A[i]⊕βj ·ΔA[i], A′[i] = A[i]⊕ΔA[i];12B[i] = B[i]⊕βj ·ΔB[i], B′[i] = B[i]⊕ΔB[i];13C[i] = C[i]⊕βj ·ΔC[i], C′[i] = C[i]⊕ΔC[i];14D[i] = D[i]⊕βj ·ΔD[i], D′[i] = D[i]⊕ΔD[i];15 end/* 加上步骤1 得到的B[0], (B,C) 有16 利用命题1, 求出B 和C 的所有值/* 在所有活跃的S 盒中, 只剩下(ΔC[1],ΔD[1]) 尚未考虑, 可17 if S(C[1])⊕S(C[1]⊕ΔC[1]) = ΔD[1]18 then 19return A ←SB-1(B) and A ⊕ΔA 20 end有8 字节差分已知*/成功的概率为2-7 */β0 ·ΔA[2] = 0, 若8 个字节已经确定*/以视作一个过滤器*//* 成功概率2-8 */

2注意到给定(Δvj,mj,Δuj) 推导16 个超级S 盒的输入输出差分时, 若对每个超级S 盒都存在一对满足条件的输入输出, 那么由此可以组合出216/2 = 215 种不同的起点, 因此需要引入15 比特的指标αj 来指示如何选择起点.

算法4 UFj 的实现Input: |mj,Δvj,Δuj;α〉|y〉, α = (α0,··· ,α14) ∈F152 Output: |mj,Δvj,Δuj;α〉|y ⊕Fj(mj,Δvj,Δuj;α)〉1 for k ∈{0,·,14} do 2ΔA(k)j ←Δvj; ΔD(k)j ←Δuj;3对函数G(k)j (mj,ΔA(k)j ,ΔD(k)j ;·) 运行Grover 搜索, 输出A(k)j [0] ∈F82 和β(k) ∈F7 2 j ←P(i)(mj,ΔA(k)j ,ΔD(k)j ,A(k)j {d-s},β(k),αj)5 end 6 ΔA(15)4A(k)j←Δvj; ΔD(15)j←Δuj;7 对函数G(15)j (mj,ΔA(15)j ,ΔD(15)j ;·) 运行Grover 搜索, 输出A(15)j {d-s} ∈F82 和β(15) ∈F7 2 8 A(15)j←P(i)(mj,ΔA(15)j ,ΔD(15)j ,A(15)j {d-s},β(15))/* 从|mj,Δvj,Δuj;α〉 生成反弹攻击起点*/9 A ←(A(0)j ,··· ,A(15)j )10 A′ ←(A(0)j ⊕ΔA(0)j ,··· ,A(15)j⊕ΔA(15)j )11 if (A,A′)满足出站差分路径then 12return |mj,Δvj,Δuj;α〉|y ⊕1〉13 else 14return |mj,Δvj,Δuj;α〉|y〉15 end

4.2 振幅放大算法实现

在3.2 节中,通过重复运行步骤(2)和步骤(3)来提高算法的成功概率,也即反复运行对UFj的Grover搜索. 注意到在量子环境下, 还可以利用振幅放大算法来改进提高成功概率的过程. 这就是说, 把步骤(1)和(2) 联合起来不进行重复运行, 整体可以看做一个过程, 它不需要给定输入而是进行一系列随机数据选取和操作, 最后(随机) 输出一对消息分组m0,m′0和一系列中间值, 使得得到反弹攻击最后一轮前只剩两列差分没有消去的状态vi-1, 而vi-1满足最后一轮88→96→16→2→16→16 的差分路线并最终得到一组碰撞的概率是2-112. 根据5 轮经典攻击的描述, 在经典环境下, 上述过程需要2128时间复杂度;而根据3.2 节, 在量子环境下, 上述过程需要288.05时间复杂度.

4.3 不使用qRAM 的改进量子碰撞算法

5 总结

我们利用振幅放大算法改进了文献[20] 中针对Grøstl-512 的5 轮量子碰撞攻击, 主要是优化了这一随机算法提高成功概率的流程,复杂度降低为原来的.可以看到,在构造与本文攻击类似地,基于反弹攻击的量子碰撞攻击时, 振幅放大算法的使用应当纳入考虑之中,它可以有效优化算法流程、提高运行效率. 振幅放大算法在这一方面仍有更大的应用空间, 值得进一步研究.