基于 ADMM 的非凸正则化轴承故障诊断方法研究
2021-03-03
北京化工大学机电工程学院 北京 100029
如今的工业生产中,机械设备不断向大型化、高速化和集成化的方向发展,在提高生产效率的同时,也带来一系列问题,比如设备长期工作于复杂工况下,测得的振动数据冗余。因此,如何从海量振动数据中获取有用的设备故障信息,成为当前设备诊断领域亟待解决的问题[1-2]。
近年来,基于l1范数正则化的稀疏表示模型在故障诊断领域得到了广泛应用,其在一定程度上降低了数据的冗余度和处理难度。然而,当故障信息非常微弱,且被淹没于多干扰源和强背景噪声中时,传统的稀疏表示模型不能得出较好的效果[3-4]。因此,一些研究人员便开展了基于非凸正则化的稀疏算法研究。在引入非凸正则化的同时,又增加了新的问题,目标函数较复杂,稀疏分解规模较大,使用传统的优化算法 (如梯度下降法、共轭梯度法)难以得到全局最优解[5-7]。针对这一问题,交替方向乘子法 (Alternating Direction Method of Multipliers,ADMM)提供了一个新的解决思路[8-9]。
ADMM 算法早在 20 世纪 70 年代就已经被提出,2010 年被 Boyd 等人[10]证明适用于具有可分离变量的大规模优化问题。ADMM 算法首先依据原始优化问题的目标函数和约束条件构造一个增广拉格朗日函数,然后通过对偶上升法交替更新变量。其本质是将原始优化问题等价分解为若干个低维子问题,使用传统的优化算法求出低维子问题的最优解,从而得到原始优化问题的全局解。多数情况下,分离得到的子问题不需要进行收敛性证明即可求得最优解[11-12]。相较于一些传统算法,ADMM 算法的求解速度快,收敛性能好,因此在统计、机器学习等领域应用广泛[13-14]。
Du 等人[15]提出了一种新型稀疏框架,即将时域波形不同,频谱相似的多个故障信号通过冗余字典来稀疏表示,把得到的稀疏系数作为优化目标函数的正则项,然后通过 ADMM 算法求解此优化问题,并使用风电场齿轮箱故障信号验证。与现有技术相比,该框架在故障诊断领域表现出一定的优越性。孙占龙等人[16]提出了一种基于 ADMM 字典学习的稀疏分解方法,该方法在字典学习阶段使用 ADMM 更新字典原子,稀疏编码阶段使用正交匹配追踪算法 (OMP)。与 K-SVD 字典学习相比,该方法构造的字典与滚动轴承振动信号更匹配,可以有效抑制原始信号中的高频噪声,准确提取故障特征。Song 等人[17]提出了一种新的滚动轴承振动信号稀疏重建算法,该算法在重构阶段采用最小二乘 QR 分解 (LSQR)算法优化 Lasso回归模型,并且使用 ADMM 算法求解该优化问题。与基追踪算法和 Lasso 回归相比,该算法重构误差较小,能在较高的压缩比下达到足够的重构精度。笔者将 ADMM 算法应用于非凸稀疏正则化问题的优化求解,充分利用了目标函数的可分离性,解决了目标函数较复杂和稀疏分解规模较大的问题。
1 ADMM 算法原理
ADMM 算法将对偶上升法的可分解性和乘子法的上界收敛性进行了整合,最初被用来求解以下等式的约束问题。
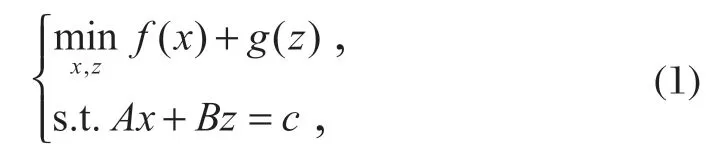
式中:x、z为优化变量。
作为一种原对偶方法,ADMM 将式 (1)中的目标函数和约束条件通过一个对偶参数耦合在一起,并且为了保证构造的函数是严格凸的,再增加一个惩罚项。于是,构成的增广拉格朗日函数为
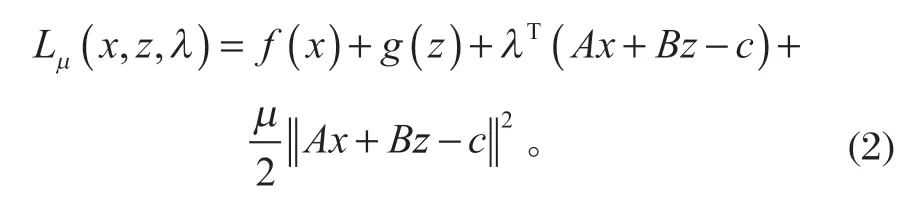
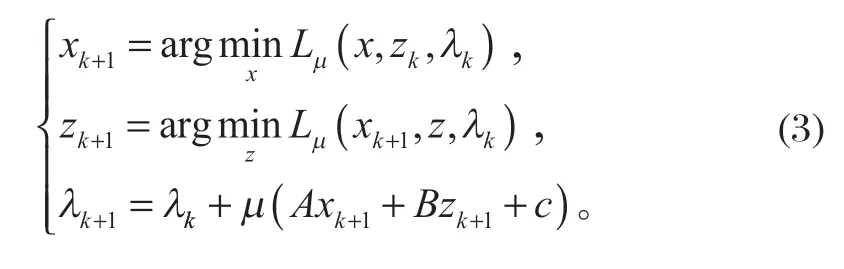
2 非凸优化稀疏表示
实际工业生产中,轴承所处的工作环境往往含有大量噪声干扰,再加上采集的振动信号故障较微弱,导致采用基于l1范数正则化的传统稀疏表示模型难以准确提取和识别信号特征频率。针对这一问题,笔者构造了一个新型稀疏表示模型,即在基于l1范数正则化的基础上增加非凸惩罚函数,然后利用 ADMM 算法进行求解。
2.1 基于 l1范数正则化的稀疏表示模型
旋转机械运行过程中,采集到的振动信号往往伴有大量的噪声干扰,因此观测信号通常表示为

式中:y为采集到的振动信号;s为仅包含故障特征的振动成分;w为噪声干扰,通常假设为高斯白噪声。
为了从采集到的振动信号y中提取出故障特征成分s,稀疏表示特征提取方法构造了如下无约束优化问题:

式中:F(x)为目标函数,由数据保真项和惩罚函数项组成;α为正则化参数,用来调节目标函数中 2 个部分的权重。
虽然基于l1范数的优化方法可以使得提取出的故障特征成分呈现稀疏性,但是往往会低估高振幅分量,导致特征成分提取不够准确[18]。基于非凸惩罚函数的优化方法可以更准确地提取信号的特征成分,考虑在传统稀疏表示模型基础上增加非凸惩罚函数,以提高滚动轴承故障特征提取精度。
2.2 非凸惩罚函数
笔者选用非凸惩罚函数来增强重构信号的稀疏性,选用的非凸函数φ∶R→R 应满足以下条件:
(1)φ在 R 范围内连续;
(2)φ在 R≠0 范围内二阶可微;
(3)φ在 R+范围内是凹函数,且是递增的;
(4)φ是偶函数;
(5)∀x≠0,。
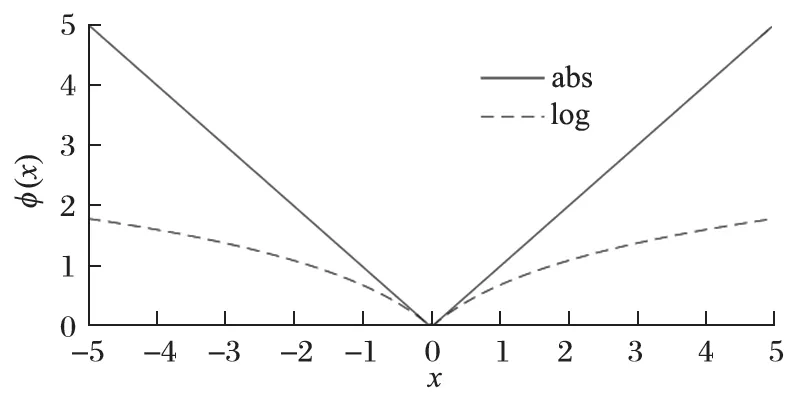
图1 绝对值函数和对数函数图像 (b=1)Fig.1 Graph of absolute function and logarithmic function (b=1)
2.3 ADMM 算法求解非凸正则化问题
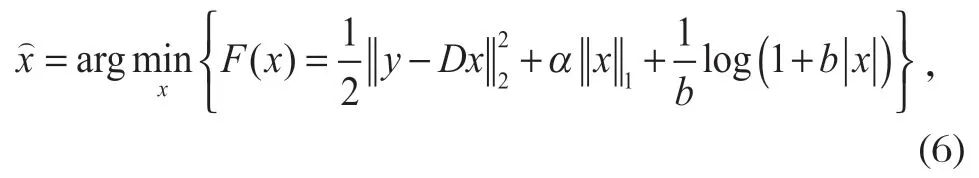
式中:b为标量参数,可以调节惩罚函数的非凸程度[19]。
将函数F对b做微分,针对不同的x取值,选取最优标量参数b。
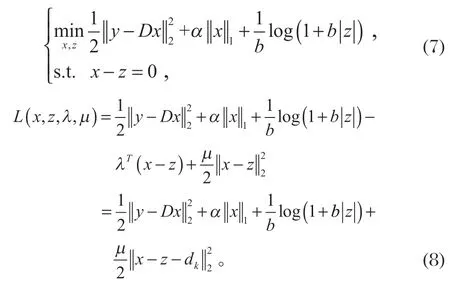
此时式 (3)变为
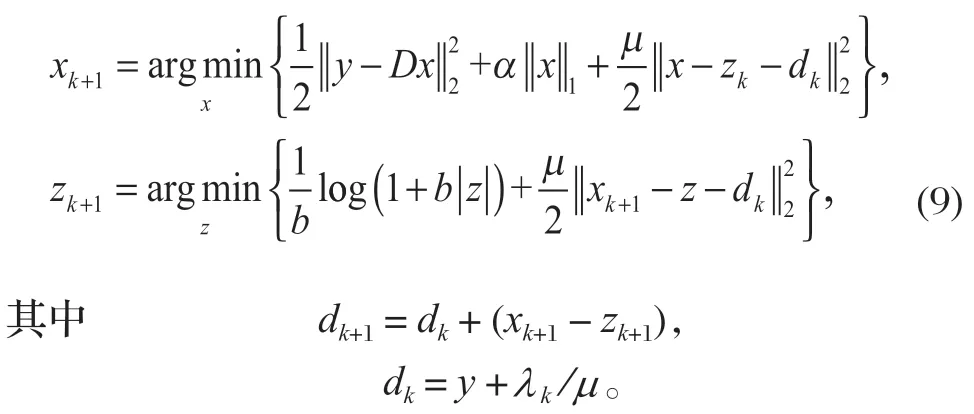
式中:x、z为优化变量;D∈RN×M为稀疏字典;y∈RN为待分析信号;λ为对偶参数;α、μ为惩罚参数。
2.4 非凸优化稀疏表示方法流程
基于上述思想,笔者提出了基于 ADMM 算法的非凸优化稀疏表示方法。轴承微弱故障诊断流程如图2 所示。
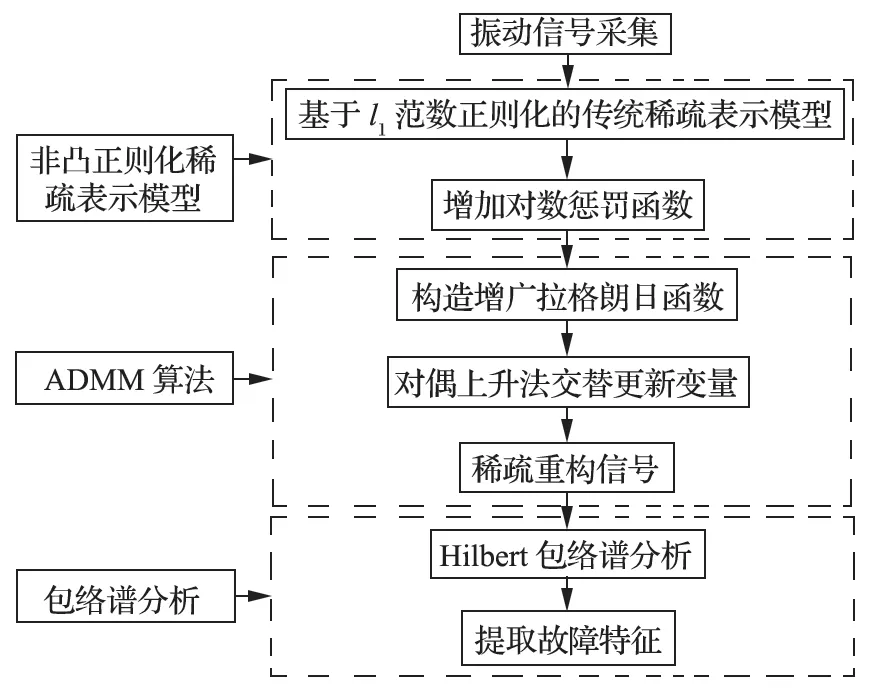
图2 轴承微弱故障诊断流程Fig.2 Process flow of bearing minor fault diagnosis
3 仿真信号验证
为了验证所提方法的有效性,采用如下仿真信号进行试验。
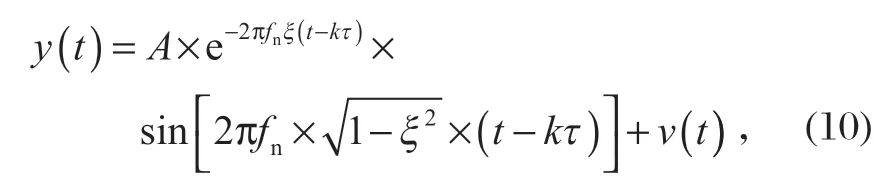
式中:A为信号幅值;ξ为衰减阻尼系数,ξ=0.1;k为周期冲击个数,k= 0,1,2,…;τ为冲击时间间隔,τ=0.02 s;fn为系统固有频率,fn=3 kHz;v(t)为高斯白噪声,用来模拟背景噪声。
采样频率为 10 kHz,故障特征频率为 50 Hz。
仿真加噪信号的时域波形图和包络频谱图如图 3所示。由图 3 可以看出,背景噪声和信号特征成分混杂在一起,在时域图和频谱图中难以区分。

图3 仿真加噪信号Fig.3 Simulation of noisy signal
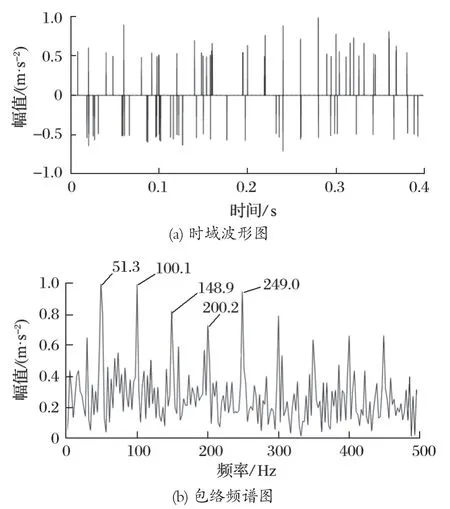
图4 改进算法的稀疏重构信号Fig.4 Sparse reconstructed signals obtained by applying improved algorithm
根据图 2 所示方法流程图,利用笔者所提方法对上述仿真加噪信号进行处理,其中标量参数b=1.25,得到稀疏重构信号的时域波形图和包络频谱图,如图 4 所示。从图 4 可以看出,原始仿真信号中的高频噪声得到有效剔除,稀疏效果好;对稀疏重构信号进行包络分析,从包络频谱图中能够较为清楚地辨认出 51.3、100.1、148.9、200.2 和 249.0 Hz 等频率成分,这与仿真加噪信号特征频率 50 Hz 的 1~5 倍频非常接近。说明采用基于 ADMM 算法的非凸优化稀疏表示方法处理仿真加噪信号,能够剔除大量背景噪声干扰,增强特征频率成分,诊断效果较为理想。
为了验证笔者所提方法的优势,与稀疏优化领域常用的 OMP 算法作对比,经 OMP 算法处理后的稀疏重构信号如图 5 所示。由图 5 可以发现,原始仿真信号中的背景噪声被剔除的同时,某些周期性冲击成分也被剔除了,特征频率增强效果明显不如笔者所提方法;对此稀疏重构信号进行包络分析,包络谱虽然能勉强提取到 51.3 Hz 的特征频率,但是其倍频成分均被淹没,且存在大量干扰谱线,并不能确定信号故障类型。由此可见,笔者所提方法在去噪和特征增强方面较 OMP 算法具有一定的优势。
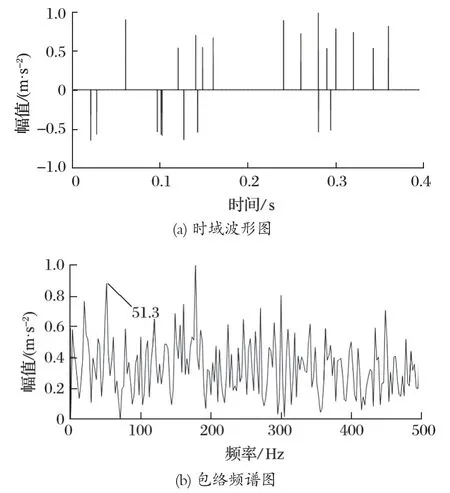
图5 OMP 算法的稀疏重构信号Fig.5 Sparse reconstructed signals obtained by applying OMP algorithm
4 试验验证
4.1 试验条件
为了再次验证所提方法的有效性,采用实测的故障轴承振动信号进行试验。采用型号为 NTN-N204的圆柱滚子轴承,利用线切割技术分别在轴承内圈和外圈上加工深度为 0.05 mm、宽度为 0.3 mm 的凹槽,将此故障轴承安装在图 6 所示旋转机械故障模拟试验台,并利用固定在轴承座 CH1 处的加速度传感器采集轴承振动信号。试验过程中,设定电动机转速为 1 300 r/min,采样频率为 100 kHz,该轴承的理论内、外圈特征频率分别为 145.8、86.3 Hz。

图6 轴承故障模拟试验台Fig.6 Bearing failure simulation test platform
4.2 试验结果
将上述采集到的轴承外圈故障振动信号截取 0.12 s,作为试验对象进行研究。轴承外圈原始信号的时域波形图和包络频谱图如图 7 所示。
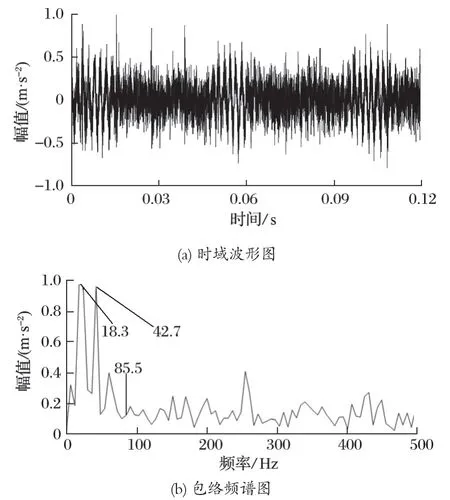
图7 轴承外圈原始信号Fig.7 Original signals of bearing outer ring
从图 7 可以看出,该原始信号含有大量噪声和谐波干扰,波形比较杂乱,冲击成分周期性不明显。对其进行包络分析,只能提取出接近轴承转频 2 倍频的频率成分 42.7 Hz,且存在干扰谱线 18.3 Hz,频谱能量集中在低频区段,转频的 1 倍频成分和故障特征成分淹没在干扰成分中,无法识别轴承故障类型。
采用非凸正则化轴承故障诊断方法对上述采集到的信号进行处理,其中标量参数b=0.52,得到稀疏重构信号的时域波形图和包络频谱图,如图 8 所示。由图 8 可以看出,原始振动信号中的高频噪声被有效剔除,稀疏效果好;对稀疏重构信号进行包络分析,从包络频谱图中能够较为清楚地辨认出 85.5、170.9、256.3、341.8 和 427.3 Hz 等频率成分,与轴承理论外圈故障特征频率 86.3 Hz 的 1~5 倍频非常接近,说明轴承外圈出现了故障。可见,非凸正则化轴承故障诊断方法能够有效提取滚动轴承微弱故障特征,实现轴承故障状态识别。
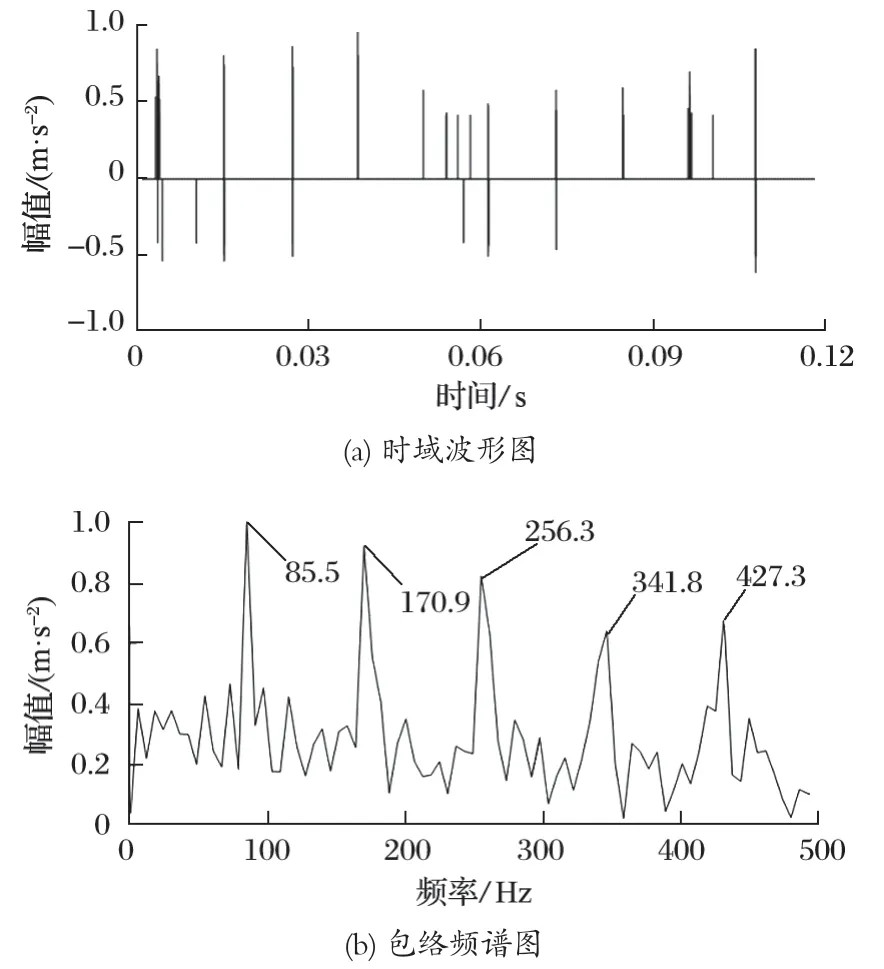
图8 轴承外圈改进算法的稀疏重构信号Fig.8 Sparse reconstructed signals of bearing outer ring obtained by applying improved algorithm
同样采用 OMP 算法对采集到的轴承外圈信号进行处理,得到稀疏重构信号的时域波形图和包络频谱图如图 9 所示。从图 9 可以看出,原始振动信号中的噪声被剔除的同时,也剔除掉了某些故障冲击,只能从重构信号中恢复一部分故障冲击成分,特征提取效果明显不如采用非凸正则化轴承故障诊断方法;对此稀疏重构信号进行包络分析,得到如图 9(b)所示的包络频谱图,虽然提取出了接近轴承转频 2 倍频的频率成分 42.7 Hz,但是转频的 1 倍频成分和故障特征成分淹没在干扰成分中,并且存在干扰谱线 18.3 Hz,无法有效诊断轴承故障。可见,基于 ADMM 的非凸正则化轴承故障诊断方法与 OMP 算法相比,有着更好的去噪能力和特征增强能力。

图9 轴承外圈 OMP 算法的稀疏重构信号Fig.9 Sparse reconstructed signals of bearing outer ring obtained by applying OMP algorithm
同样将试验中采集到的轴承内圈故障信号截取0.12 s,作为试验对象开展研究。轴承内圈原始信号如图 10 所示,时域图的波形杂乱,冲击成分被背景噪声淹没,冲击成分周期性不明显。这可能是由于故障尺寸较小,与噪声成分相比能量较微弱。对其进行包络分析处理,只能提取出接近轴承转频 2 倍频的频率成分 42.7 Hz,且存在较多干扰谱线,转频的 1 倍频成分和故障特征成分淹没在干扰成分中,无法识别轴承故障状态。
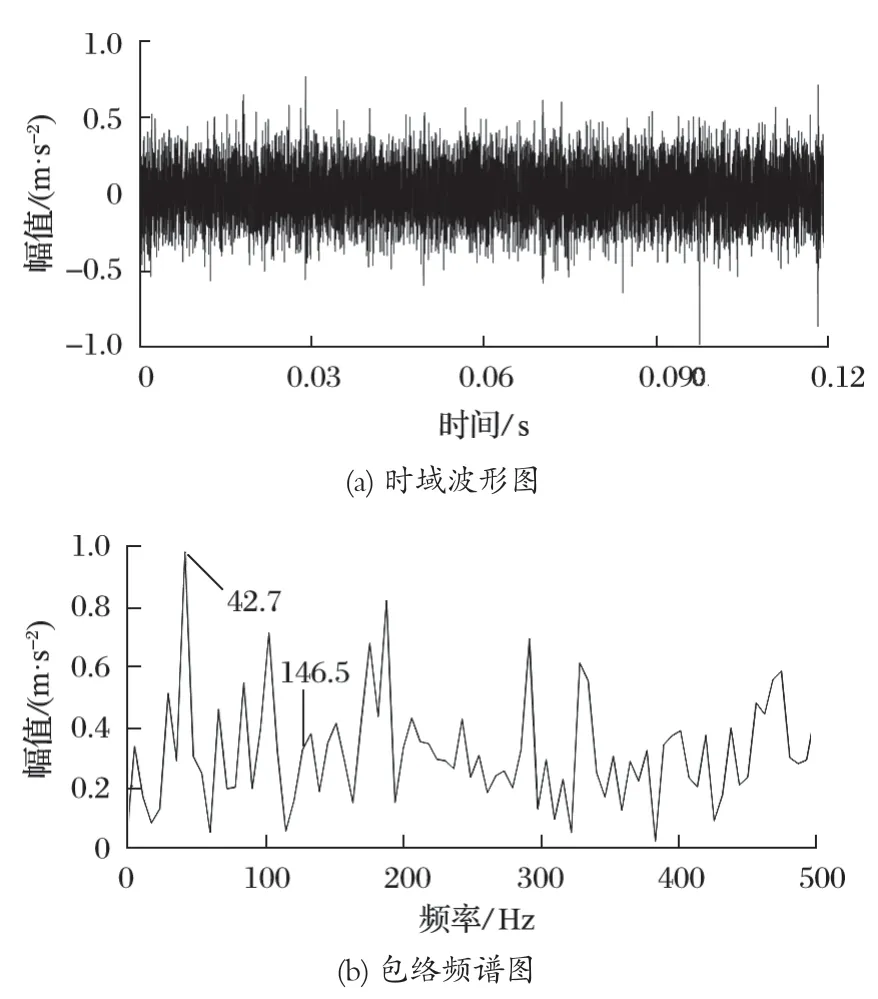
图10 轴承内圈原始信号Fig.10 Original signals of bearing inner ring
采用非凸正则化轴承故障诊断方法对上述试验采集的内圈故障信号进行处理,其中标量参数b=0.84,得到稀疏重构信号的时域波形图和包络频谱图,如图 11 所示。由图 11 可以看出,此方法能够有效消除原始信号中的噪声干扰,稀疏效果好。对稀疏重构信号进行包络分析,其中 42.7、146.5 和 293.0 Hz 等频率成分被提取出来,这分别与轴承转频的 2倍频,轴承理论内圈故障频率 145.8 Hz 的 1、2 倍频非常接近。虽然干扰谱线仍然存在,但是能够辨认出此时轴承内圈发生了故障。轴承转频的 2 倍频被提取出来的原因可能是试验装置存在缺陷 (例如结构未对中)。
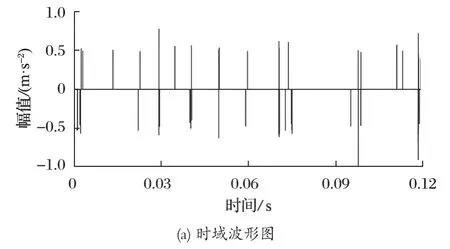

图11 轴承内圈改进算法的稀疏重构信号Fig.11 Sparse reconstructed signals of bearing inner ring obtained by applying improved algorithm
为了进一步验证笔者所提方法的优势,同样采用OMP 算法对采集到的轴承内圈信号进行处理,得到稀疏重构信号时域波形图和包络频谱图,如图 12 所示。由图 12 可以看出,原始振动信号中的噪声被剔除的同时,也剔除掉了某些故障冲击,只能从重构信号中恢复一部分故障冲击,特征提取效果明显不如采用非凸正则化轴承故障诊断方法;虽然包络谱提取出了 42.7 和 146.5 Hz 频率成分,但是干扰谱线的能量占据主导地位,故障特征频率的幅值较小,无法识别轴承故障类型。可见非凸正则化轴承故障诊断方法较OMP 算法在去噪和特征增强方面具有一定优势。
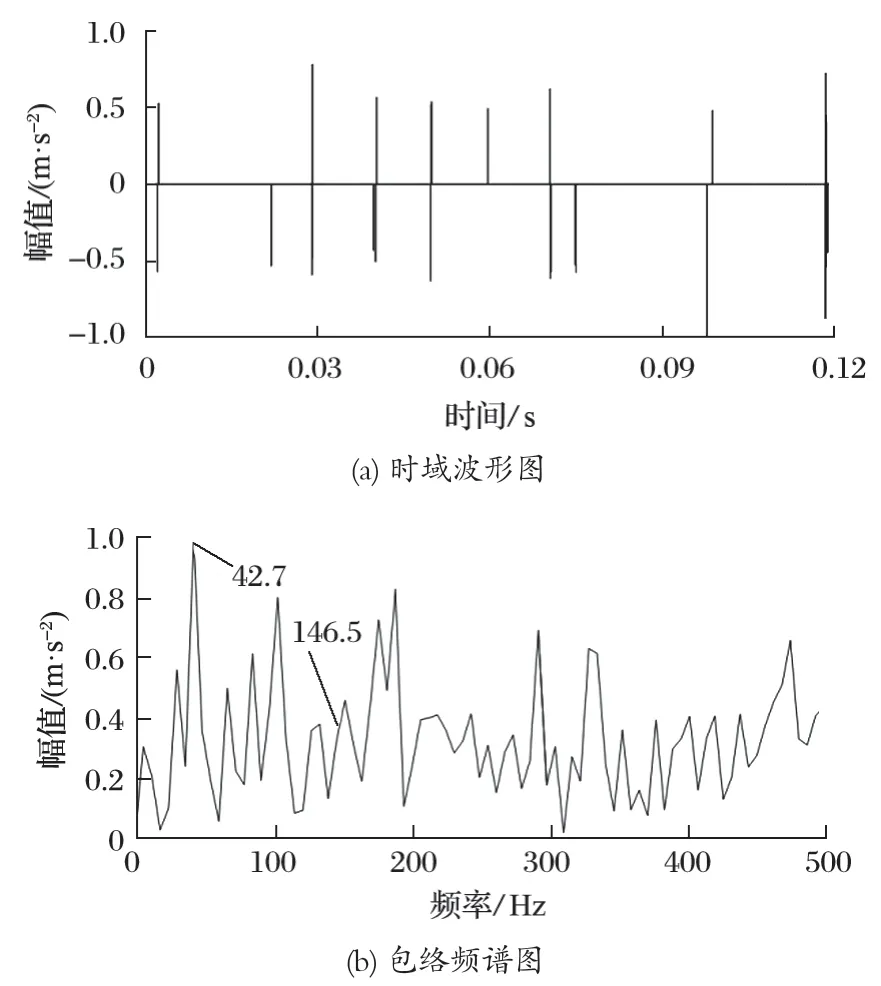
图12 轴承内圈 OMP 算法的稀疏重构信号Fig.12 Sparse reconstructed signals of bearing inner ring obtained by applying OMP algorithm
5 结语
通过利用基于 ADMM 的非凸正则化轴承故障诊断方法对复杂工况下轴承微弱故障信号进行提取,以仿真加噪信号和滚动轴承实际信号作为试验对象进行验证。试验结果表明:基于 ADMM 的非凸正则化轴承故障诊断方法显著消除了原始信号中的噪声干扰,有效增强了微弱故障特征,并实现了振动信号微弱故障的准确诊断。该方法在基于l1范数正则化的传统稀疏模型基础上增加了对数惩罚函数,增强了微弱故障特征,解决了传统稀疏表示模型难以准确提取微弱故障特征的问题。引入 ADMM 算法,解决了加入非凸惩罚函数后目标函数复杂,无法使用单一优化算法求解的问题。
