基于非线性波动网络模型的股票市场关联特征研究

李为波，郭雪

(武汉纺织大学经济学院，湖北 武汉 430200)

0 引言

近年来，复杂理论应用于金融领域的研究越来越多，将证券市场看成一个系统，研究系统中金融个体之间的相互影响.因此，基于网络理论构建金融网络来解释并研究证券市场中股票之间的相互关系具有重要意义.以证券市场为例，将证券市场上的每只股票看成是该网络的节点，从复杂网络的角度分析股票市场中股票之间的关联性和等级聚类结构.这方面开创性的研究可参考文献[1-2].

复杂网络理论可以解决金融市场中的投资组合优化和风险管理等方面的问题(Heiberger，2014；Longfeng Zhao，2016)[3-4]，这类研究通常以股票价格的影响力或对数收益率作为研究对象，以收益率的相关系数度量两个节点股票之间的联系，在此基础上建立股票网络.在现有的文献中，度量股票价格波动之间相关性的工具主要是Pearson相关系数[2，5]，Pearson相关系数主要测度变量间的线性相关关系，又因其具有比较好的性质，应用比较广泛.随着金融市场的发展，金融变量之间的价格波动关系呈现出非正态分布及非线性等特征，如果以线性相关系数的方式度量，会掩盖金融市场波动信息的损失，无法体现市场的风险特征.Carsten等(2004)[6]提出以互信息(mutual information，简写为MI)为基础建立基因网络，互信息是基于信息理论的测度方法，可以度量各种类型的相关关系.Fiedor(2014)[7]将互信息和互信息率运用于股票网络，并与相关系数进行比较；在此基础上，Guo等(2018)[8]及宁瀚文等(2019)[9]将互信息引入股票市场分析市场结构及风险特征.

在构建网络方面，研究者根据需要运用不同的算法构建金融网络.常见的有最小生成树法(minimal spanning trees,简写为MST)，极大平面过滤图(planar maximally filtered graph,简写为PMFG)和相关系数阀值法(asset graph).MST构造的网络结构是最精简的，在N个节点的网络中，MST生成N-1条边(Aste等，2004)[10]，而在PMFG中(Tumminello,2006)[11]，每个节点至少与其他两个节点相连，共生成3N-6条边，从聚类的角度分析网络拓扑结构特征.Tumminello(2008)[12]选择了美国纽约证券市场上2001—2003年间资金集中的300只股票，PMFG保留了股票之间更多的聚集信息.相关系数阈值法(Onnela,2004)[13]根据网络中所有节点两两之间的相关性程度排序，给出一个阈值水平，超过阈值水平的节点之间相连.

本文中以信息理论为基础，提出非线性关系网络模型的构建.已有的非线性关系研究中，互信息在离散变量相关性的度量中，需要对时间序列进行网格的划分，网格的规模及划分形式对互信息的度量有一定的干扰.Reshef(2011)[14]提出最大信息法，通过网格优化的方式测度非线性关系，相比互信息，最大信息法更具优势.因此，本文中以最大信息法作为变量间关联性的度量工具，构建股价波动网络模型，从相似性和差异性两方面刻画股票网络的聚类特性，探析股票市场中信息的传导机制，揭示股票在信息传递中的地位和功能.实证分析选择的样本为上证180指数中金融成分股票时间序列，验证股票价格波动非线性网络模型的应用价值.

1 理论模型

1.1 互信息互信息是信息论里一种有用的信息度量，它反应变量间广义的相关程度，反映一个随机变量中包含的关于另一个随机变量的信息量，也即一个随机变量由于已知另一个随机变量而减少的不确定性.

“信息熵”解决了对信息量化度量问题，一条信息的信息量大小决定于它的不确定性.对于任意一个离散随机变量X，它的熵(1)一般情况下，log是以2为底，因此香农熵是用比特(bit)这个概念来度量信息量.比如，投掷一枚质地均匀的硬币，它的熵为1比特，特殊情况有0log=0定义如下：

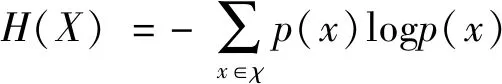
(1)

记事件x发生可用随机变量x表示，发生的概率记作p(x)，即事件发生所提供的信息量I(x)是该事件发生的先验概率p(x)的函数I(x)=-log(p(x))，其中p(x)为消息的先验概率，我们称I(x)为自信息量，表示当事件x发生以前，I(x)是事件x发生的不确定性；其次当事件x发生以后，I(x)表示事件x在无噪声情况下所提供的信息量.

对于一组随机变量(X,Y)的联合熵和单个离散随机变量的熵定义类似，(X,Y)看成向量随机变量，联合熵H(X,Y) 定义为：

(2)

相应地，互信息公式可以表示成：

I(X;Y)=H(X)+H(Y)-H(X,Y)

(3)

其中，H(X)>0，H(Y)>0，H(X,Y)>0，I(X;Y)>0.如果是连续型随机变量，类似地利用概率密度函数来计算香农熵.

公式(2)～(3)是互信息的理论公式，应用前需得到随机变量的概率分布，在实际应用中随机变量的概率分布通常是未知的，在数据量足够的前提下，我们考虑采取频率分布替代概率分布，具体计算过程如下：

(4)

类似可计算X和Y的联合熵：X和Y在 [minX，maxX]×[minY，maxY] 区域时，将该区域划分成k1×k2个等间距区域(k1，k2为正整数)，分别计算(X,Y)在每个区域的频数，记fq,r为(X,Y)在区域(q,r)里的频数，则(X,Y)的联合频数分布：

(5)

则随机变量X和Y之间的联合熵为：

(6)

注意到，每个网格在X方向和Y方向上分别是等间距的.当pq,r=0时，即区域(q,r)里的频数为0，pq,rlogpq,r=0.

最后，将计算得到的H(X)，H(Y)以及H(X,Y)代入式(3)，则可得到随机变量X和Y之间的互信息量.为了便于比较，对式(3)进行标准化，可得到X和Y的标准互信息量(2)在后面没有特别说明的条件下，提到的互信息均是标准化后的互信息：

(7)

标准化的互信息值取值范围为0-1，根据数值大小，我们可以判断X和Y之间相关性强弱.

1.2 最大信息系数最大信息系数(maximal information coefficient，简称MIC)，衡量两个变量X和Y之间的(线性或者非线性)关联程度(Reshef,2011)[14],它属于最大的基于信息的非参数性探索(maximal information-based nonparametric exploration，简称MINE).该方法取值的大小仅与变量之间相关性强弱有关，而与变量之间的函数关系无关.当样本容量足够大时，能够捕捉各种形式的关联(郭雪，2018)[15].

最大信息系数法是以互信息为基础，在X，Y方向上分别划分一定的区间数，即通过k1，k2的选择使得随机变量X，Y的互信息量达到最大.最大信息系数的计算公式可表达为

(8)

最大信息系数的计算步骤与计算互信息量过程类似：第一步，给定k1，k2，对X，Y构成的散点图进行网格化，根据式(4)～(6)计算最大的互信息值，式(8)中|X| (|Y|)代表在X(Y)方向上总共被分成多少段，且|X||Y|

2 实证分析

2.1 样本选择选取上证180指数金融成分的股票作为样本进行实证分析，上证180指数的股票市值规模大、流动性好，因此具有较强的代表性.由于各个金融机构上市时间不一致，剔除研究期内数据不全的金融机构，从2014年1月2日—2020年7月31日，共有34家金融机构符合样本要求.对于样本期间因停牌导致的股票价格数据缺失采取停牌前的最后一个交易日的数据替代.

为了研究股价波动之间的非线性相关，本研究选取两个指标进行分析，一个是以股价的对数收益率为指标：考虑n支股票，pi,t和pi,t-1为第i只股票第t个和第t-1个交易日的收盘价，定义Ri,t为第i只股票在第t个时间段收益率：Ri,t=ln(Pi,t/Pi,t-1)，(i=1,2,…，n,t=1,2…，d)，这样可以去除随机趋势；第二个指标是选择股票的换手率，换手率越高，股票的交易越活跃，股价波动也就越明显.

在已有的研究中，两只股票间的线性相关系数计算公式为：

(9)

2.2 线性相关系数、互信息与最大信息系数的比较为了比较互信息和最大互信息在度量股票价格波动之间相关影响的特性，我们分别采用线性相关系数、互信息和最大信息系数计算股价对数收益率和换手率的相关性.在计算互信息时，需将收益率区间平均分成若干个子区间，本文划分为10个子区间，每个子区间步长为l=0.02，根据每只股票在样本研究期内的股价收益率的最大值和最小值确定区间范围，再由式(4)计算股价波动落到每个子区间的频率，再代入到式(5)和(6)中计算互信息.

图1 基于3种方法计算相关性的分布图

表1 股价波动相关性的描述性统计分析

由于股价收益率指标是根据每日收盘价数据计算得到的，会丢失很多每日交易的信息，换手率反映了股票的交易活跃程度和流通性，直接导致股价的波动，因此我们考虑换手率指标分析股价波动的相关性.表1给出了基于换手率相关性度量的统计分析，图1(A)～(F)分别为基于换手率的线性相关系数、互信息及最大信息系数的分布图.从表中数据对比发现，无论用哪种方法计算，股票换手率之间的相关性更强.线性相关系数的取值为[-0.111 9,0.924 5]，标准差为0.279 7，仅有4.28%的股票对之间存在非常弱的负相关；互信息取值为[0.013 5,0.568 6]，标准差为0.140 4；最大信息系数取值范围为[0.289 3,1]，标准差为0.139 6；相比之下，最大信息系数对非线性的识别更加敏感.从分布图上看，线性相关系数的分布出现了明显的双峰，在0附近出现了一个峰值，互信息的分布中有一小部分比例聚集在0附近，而最大信息系数的分布适中，具有良好的区分度.

3种方法进行比较，与线性相关系数相比，互信息和最大信息系数能够较好地识别变量之间的非线性影响，最大信息系数在非线性的区分度上比互信息更具有优势.由于互信息划分的区间模式和数量的调整，对计算的结果产生一定的偏差，而最大信息系数是从所有可能的互信息值中选取最大值.在计算互信息划分收益率区间时，还可由中国股市的交易规则“每日的涨跌幅不超过10%”，将收益率区间统一设置为[-10%,10%]；其次，子区间个数k的选择，随着k的增加，结果的精确度越高，Fiedor(2014)[7]指出当区间划分网格超过10个及其以上时，平均绝对误差越来越小.在以股价对数收益率为指标计算的过程中，有涨跌幅的限制，所以区间的改变对结果影响不大，但是在以换手率为指标的计算中，换手率的取值没有范围限制，所以区间模式和数量的调整对互信息的结果有一定的干扰.

3 网络模型的构建

3.1 极大平面过滤图算法股票价格的波动具有聚类效应，在得到股票两两之间相关性的基础上，我们构建网络模型分析股票之间的聚类效应，对网络中的聚类信息进一步筛选，主要研究网络中小规模的聚类，也可称为小集团(clique).小集团一般是由3个及3个以上的节点组成的全连通子网络KN(N≥3)，即集团内的任意两个节点之间直接相连.分析集团内部的结构，比较聚类的相似性和差异性.

如果能将网络图在平面内画出且使其边各不相交，那么这个图就是可平面的，否则是不可平面的.当网络图的边数达到最大且被画成平面图时，称为极大平面过滤图(PMFG).该网络图基于平面图的前提下，提取较强相关性的边，从而分析聚类过程中的相似性和差异性.该算法构建网络的过程为：第一步，计算邻接矩阵AN×N，即相关性度量矩阵；然后对矩阵里的上三角(或下三角)元素从高到低排序；第三步，从最高相关性的边开始逐步连接，每增加一条边都要验证是否构成K3，最后输出边集合和节点集合，构建网络.

3.2 网络拓扑结构分析根据上述算法，我们得到样本在研究周期内的极大平面过滤图(如图2和图3).图中34个节点由96条边连接起来，不同节点在网络中的地位不同.在无权关联网络中，节点vi的度ki定义为与该节点连接的边数.一个节点的度越大，这个节点在某种意义上越重要.以股价对数收益率为基础构建的股价波动网络中，平均度为5.647 1，中信证券(600030)、兴业银行(601166)、光大证券(601788)和兴业证券(601377)居于中心位置，节点度分别为12，12，11，10；光大银行(601818)和华夏银行(600015)为次中心节点，节点度均为9.以换手率为基础构建的股价波动网络中，平均度为5.647 1，华夏银行(600015)和工商银行(601398)是网络中心节点，节点度分别为10和13，国金证券(600109)、恒生电子(600570)和华泰证券(601688)居于次中心位置，节点度均为9，网络中其他股票节点度相对比较低，处于边缘位置.从节点度分布不难发现，股票网络中具有影响力的股票仅占少数，大多数股票节点处于被影响的地位.

图2 股价对数收益率相关性网络

图3 股票换手率相关性网络

为了进一步揭示信息在网络中传递的特征，本研究分析小集团特征对网络聚集.在股价对数收益率相关网络中，产生了11个K4和16个K3，从这27个集团内部的角度考虑，集团的平均最大信息系数落在区间[0.288 8，0.517 0]内；在换手率相关网络中，一共构成了14个K4和13个K3，平均最大信息系数位于区间[0.694 0，0.943 1]内(4)K4中4个节点两两相邻，则任意3个节点也是两两相邻，但不能说K4包含K3.

集团特征反映了股票节点之间的相似性，那集团内部的股票之间关联性的差异性则通过每两个节点之间相关系数占集团内部相关系数和的比值的平方和来度量(Tumminelloet等，2005)[11]，即：

(10)

我们分别考虑K4和K3的内部差异性，股价对数收益率相关性网络中，K4的内部差异值主要集中在[0.166 8，0.182 8]；K3的内部差异值落在[0.333 8，0.369 6]；换手率相关性网络中，K4的差异在[0.167 2，0.169 5]；K3的内部差异值落在[0.333 3，0.342 0].由此可知，极大平面图在构建网络时既考虑了聚集特征，又体现出相关性水平的差异性.PMFG在经过平面嵌入时，充分体现了网络层级结构的特征，保证了相关性在不同水平的股票节点都能包含进小集团.

4 结论

本研究基于股票价格波动相关性的背景，介绍了以信息论为理论基础的相关性度量方法，互信息和最大信息系数，并与线性相关系数进行对比.以上证180指数金融成分股票为研究样本，选取股价对数收益率和换手率为指标，用3种不同方法分别度量股票价格波动之间的关联性.实证分析可知，线性相关系数主要度量线性趋势，在该样本中，线性相关系数的度量呈现出双峰状态，部分股票对之间的相关系数聚集在0附近；而以互信息值和最大信息系数为关联的度量方法，可以较好地识别股票之间的非线性趋势，互信息值在计算的过程中受到网格划分的影响，结果存在一定的偏差，最大信息系数能够较好地区分不同程度的非线性趋势.因此，在非线性相关性的度量中，最大信息系数具有优势.

然后基于最大信息系数构建股价对数收益率和换手率的相关性网络，考虑到股票价格波动的聚集性，我们采用极大平面过滤图的算法构建网络，通过对网络拓扑特征的统计分析，发现股票网络中仅有极少数的股票节点属于具有影响力节点，大多数股票节点处于被影响的地位.此外，股票网络中信息的传递具有分层特征，信息在网络不同层级间传播，有助于分析金融风险的传播方式及途径.

本文中的研究方法可以进一步地拓展应用于建立高维度金融网络模型，尤其是在金融大数据背景下，可以更全面地挖掘金融市场的内部特征，从风险传染及预警的角度为当前的金融体系提供实践意义.