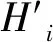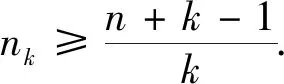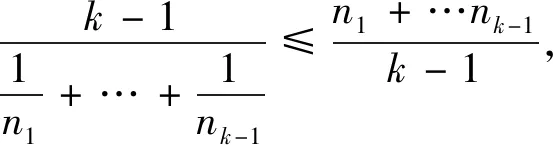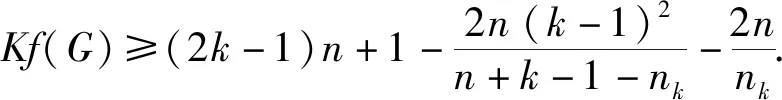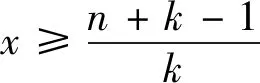图的基尔霍夫指数的下界
2021-03-03喻莹莹高珊
喻莹莹,高珊
(1.湖北大学数学与统计学学院,湖北 武汉 430062;2.湖北大学计算机与信息工程学院,湖北 武汉 430062;3.应用数学湖北省重点实验室(湖北大学),湖北 武汉430062)
0 引言
设G=(V(G),E(G))是一个有限的简单无向图,G中顶点数|V(G)|称为图G的阶数.对图G的任意顶点x,G-x是指从G中删除顶点x后得到的图,G-xy是指从G中删除边xy后得到的图.设G是连通图,如果G-x不连通,那么顶点x成为G的的割点或分离点.图G的极大不可分离图称为G的块(block).图G的每一个阶数至少为3的块是2-连通的.如果连通图G的每个块都是完全图,则称G是块图.n阶完全图和n阶星图分别记为Kn和Sn.
图G中顶点u到顶点v的最短路的长度称为顶点u与v间的距离,记为dG(u,v).图G中顶点u到顶点v的有效电阻距离记为rG(u,v).图G的基尔霍夫指数Kf(G)定义为
Kf(G)=∑u,v∈V(G)dG(u,v).
点v到图G中其余所有点的电阻距离之和,定义为Kfv(G)=∑u≠vr(v,u),记为Kfv(G).在不引起混淆的情况下,常用d(u,v),r(u,v)来代替dG(u,v),rG(u,v).

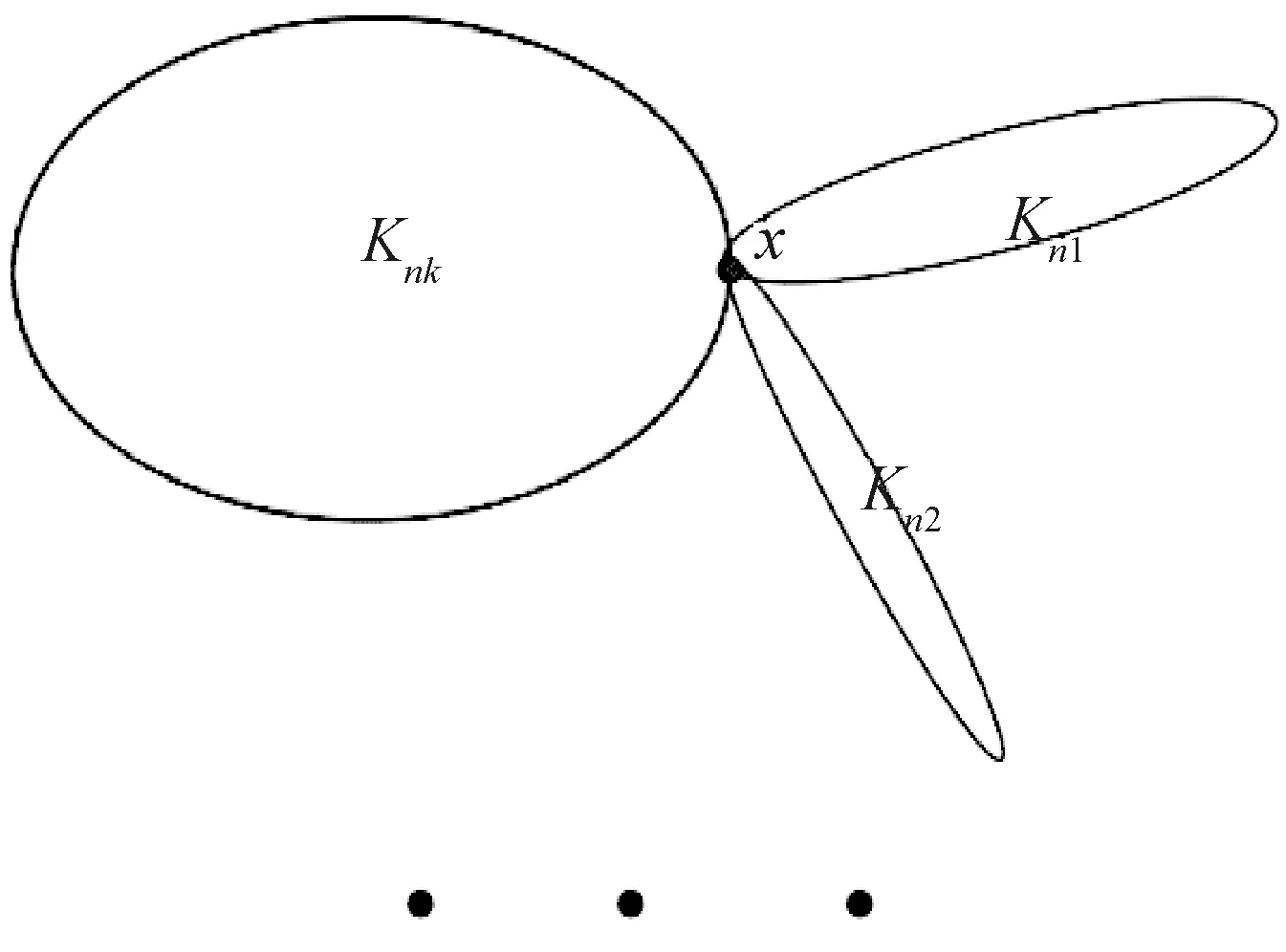
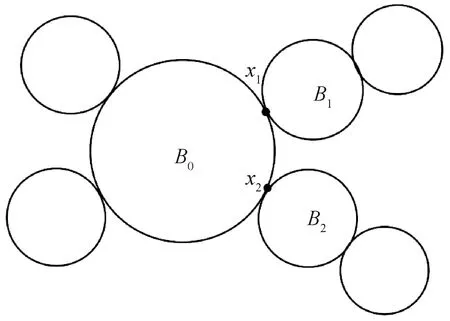
图1 S[n1,n2,…,nk]
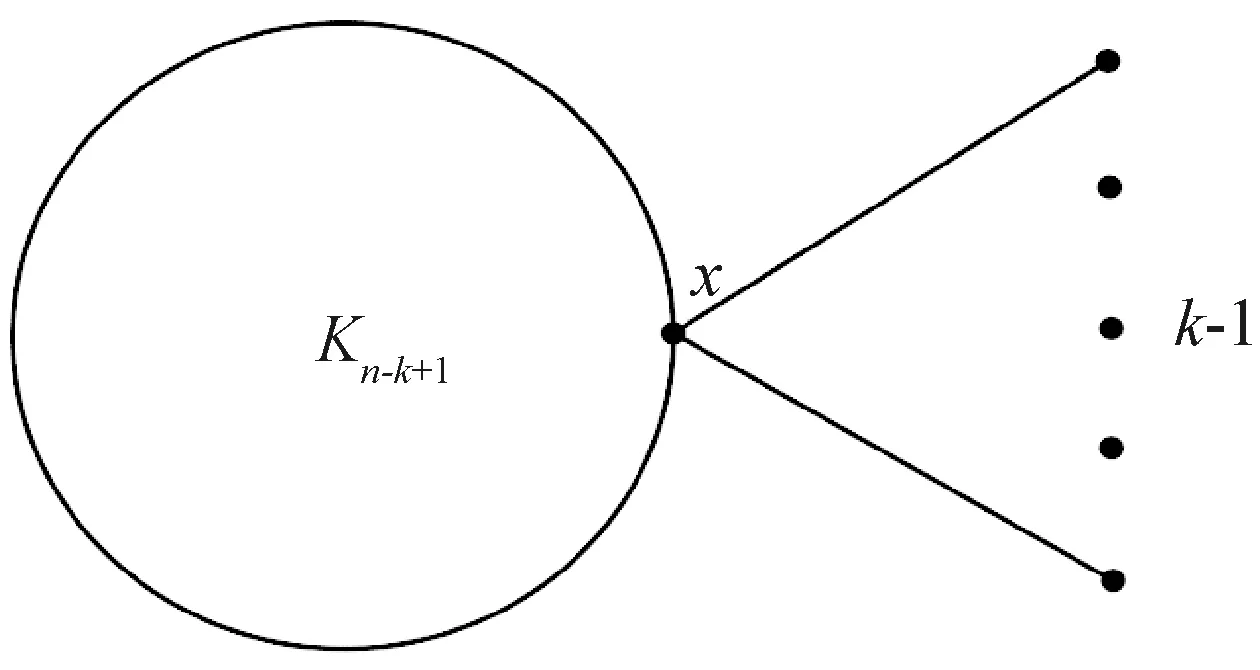
图
设G是一个连通图,G1和G2是G的两个非空连通子图,若V(G1)∩V(G2)={x},则记G=G1xG2.本文中没有给出的符号和概念可参考文献[8-9].
1 基尔霍夫指数的性质
本节中我们给出了图基尔霍夫指数的基本性质及相关运算,这些性质和运算在本文中主要结论的证明中经常用到.
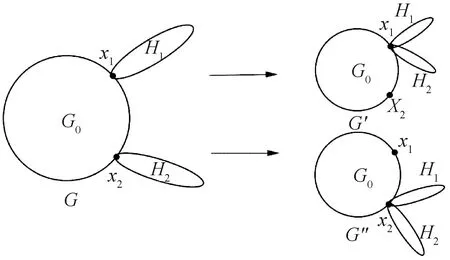
引理1[10]设图G=(V(G),E(G))是非完全图.若uv∉E(G),则有Kf(G+uv) 引理2[6]设图G1,G2是两个连通图,令G=G1xG2,其中V(G1)∩V(G2)={x},则有 Kf(G)=Kf(G1)+Kf(G2)+(|V(G1)|-1)Kfx(G2)+(|V(G2)|-1)Kfx(G1). 引理3[11]设图G是一个连通图,x是图G的割点,令G1和G2分别是G-x两个的连通分支,则对于任意的a∈V(G1),b∈V(G2),均有rG(a;b)=rG1(a;x)+rG2(x;b). 引理4[10]n阶完全图的基尔霍夫指数具有下列性质: 1)Kf(Kn)=n-1; 命题5对任意的星块图G=S[n1,n2,…,nk],我们有 (1) 命题5的证明对k归纳证明(1)式.当k=1时,S[n1,n2,…,nk]=Kn1,则由引理4可知Kf(G)=n1-1,即(1)式成立.当k=2时,则由引理2和引理3可知 即(1)式成立.假设2≤k 又由引理2和引理3可知 即k=l时,(1)式成立,从而 本节中我们研究具有k个块的n阶连通图的基尔霍夫指数. 令Bn,k={G:G是一个有k个块的n阶连通图}.注意到Bn,1={Kn}.因此下面可以假设k≥2.在给出我们的主要结果之前,先证明如下的引理. 图3 G,G′,G″ 引理6的证明由引理2可知 于是 =(|V(H2)|-1)[Kfx2(G0)+r(x2,x1)(n(H1)-1)+Kfx1(H1)-Kfx1(G0)-Kfx1(H1)] =(|V(H2)|-1)[Kfx2(G0)-Kfx1(G0)+r(x2,x1)(|V(H1)|-1)] (2) 类似地,可得 Kf(G)-Kf(G″)=(|V(H1)|-1)[Kfx1(G0)-Kfx2(G0)+r(x1,x2)(|V(H2)|-1)] (3) 如果Kfx2(G0)≥Kfx1(G0),则由(2)式及r(x2,x1)>0,|V(H1)|≥2可知:Kf(G)>Kf(G′). 如果Kfx1(G0)≥Kfx2(G0),则由(3)式及r(x1,x2)>0,|V(H2)|≥2可知:Kf(G)>Kf(G″). 接下来证明下面的论断. 推论1G=S[n1,n2,…,nk],这里n1+n2+…+nk=n+k-1. 图4 G 由调和平均数与算数平均数的关系可知: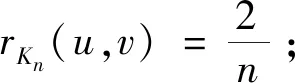

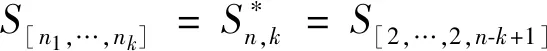
2 主要结果