浅谈教材的创造性使用

汪昭潮

教师要创造性地使用教材，用教材教，而非教教材。笔者以人教版四年级下册第三单元《乘法分配律》的教学为例，浅谈如何创造性地使用教材。

一、置换情境，激发学习兴趣

兴趣是最好的老师。当教材提供的情境离学生较远时，教师可以置换情境，激发学生的学习兴趣。

《乘法分配律》教学中，教材选取的是植树情境：参加植树活动的同学一共有25个小组，每组4人负责挖坑种树，2人负责抬水浇树，要求一共有多少人。由于很多学生没有参加集体植树活动的生活經验，很难激起他们的学习兴趣。因此，笔者根据执教班级学生的特点，尝试更换学生更加熟悉的场景。教学片段如下：

师：学校每个月都要收取午餐费，每个学生每餐是12元，五（5）班有男生24人，女生20人。对此你能提出什么数学问题？

生1：五（5）班一天要交多少餐费？

生2：五（5）班男生一天交多少餐费？

生3：五（5）班女生一天交多少餐费？

生4：五（5）班一个月要交多少餐费？

……

师：大家提的问题都很有意义，我们这节课主要解决第一个问题：五（5）班一天要交多少餐费？哪位同学愿意上台来交流你的算法？

生5：我们可以先算出全班男生一天的餐费，即12×24=288（元），再算出全班女生一天的餐费，即12×20=240（元），然后把这两个结果相加，即288+240=528（元）。

生6：我和他的方法一样，用的综合算式：12×24+12×20=528（元）。

生7：我是先算出全班总人数，24+20=44（人），因为每人餐费12元，所以全班总共餐费是12×44=528（元）。综合算式是12×（24+20）=528（元）。

师：这两种不同的方法都能正确求出全班的总费用，说明这两个综合式有什么关系？

生（齐）：相等。

师：关于这两个相等的综合算式，同学们有什么要提醒别人要注意的吗？

生8：12×（24+20）≠12×24+20，不能直接把括号拿掉，等号右边应当是两个乘法算式，里面都要有12。

生9：我补充，因为12×24表示男生一天的餐费，而20是女生人数，男生一天的餐费和女生人数相加没有意义。

“收餐费”这一和学生生活息息相关的情境，能激活学生的生活经验，激发学生的学习兴趣，让学生认真参与到教学活动中。在教师的引导下，学生把目光聚焦到提出的第一个问题，兴致勃勃地去解决它。此外，学生还能结合这一具体事例，解释为什么“12×（24+20）≠12×24+20”，从而在理解的基础上认识了乘法分配律的基本特征，为正确抽象出乘法分配律模型奠定基础。

二、增添素材，丰富认知体验

数学是抽象的学科，抽象是数学学习的重要目标。仅仅使用上述一个例子必然会造成学生感知素材单一、体验匮乏，达不到抽象出乘法分配律模型的要求。这个时候，教师需要适当增加一些素材，让学生在多样化的情境中，充分积累经验，丰富认知体验，加深对乘法分配律特征的认识。

首先，教师可以创造性地使用课本例题，让学生用两种不同的方法求参加植树的人数;然后，创编一道求长方形植树地周长的题（如下图），让学生结合长方形实物图，说明两种求周长的方法分别是（37+13）×2和37×2+13×2;最后，让学生根据上述算式的特征，举出一些类似的例子，让学生对乘法分配律的特征有足够清晰的认识。有了上述充足的认知体验后，再让学生尝试抽象出乘法分配律的字母公式“（a+b）×c=a×c+b×c”，就水到渠成了。

三、多维思考，探寻内在道理

在抽象出数学模型后，教师可以让学生多维度探寻内在道理，加深对知识的理解。教师可以通过提出“怎样理解a×（b+c）=a×b+a×c呢？”这个问题驱动学生的思维走向更深层次，去探寻知识的本质。

首先，学生已经有了上面例题的铺垫，会从整数乘法的意义去解释：a×（b+c）可以理解为（b+c）个a的和，a×b可以理解为b个a的和，a×c可以理解为c个a的和，因此（b+c）个a的和就等于b个a的和加c个a的和。

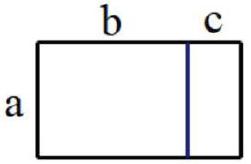
其次，乘积与长方形的面积计算可以密切结合起来，教师可以构造出求长方形面积的直观图形来解释乘法分配律（如下图）。

求大长方形的面积有两种思路。一是分别求出两个小长方形的面积，即左边长方形的面积为a×b，右边长方形的面积为a×c，再把两者相加，所以整个大长方形的面积可以表示为：a×b+a×c。第二种思路是把上图看作一个整体，长为（b+c），宽为a，所以大长方形的面积也可以表示为a×（b+c）。既然都是求长方形的面积，那么自然可以得到a×（b+c）=a×b+a×c。结合图来看，乘法分配律可以这样理解：乘法分配律的实质就是对大长方形面积求法的两种不同方法，要么先求出每个小长方形的面积，再把二者相加，要么当作一个整体，先求出大长方形的长再直接求大长方形的面积。更简单地说，就是大长方形的面积，可以先求部分再求和，也可以整体来算。

四、适度拓展，诱发头脑风暴

数学课绝不仅仅是教学知识、技能，更重要的是数学承载着发展人的思维的功能。作为一名数学教师，要给学生提供良好的平台，让学生的思维得到充分发展。

在经过上述充分的挖掘后，教师还可以围绕乘法分配律进行适度的拓展，放飞学生的思维，诱发一场头脑风暴。比如a×（b-c），括号里是两个数的差，应该等于什么？a×（b+c+d），括号内部推广到三个数，又该等于什么？甚至还可以将括号内的数推广到n个，即a×（b1+b2+…+bn）又等于什么？学生有了对上述知识的探索，推理能力、创新能力都会得到显著提升。

（作者单位：武汉经济技术开发区神龙小学）

责任编辑 张敏