基于元胞自动机微观模拟的随机车流与桥梁耦合振动数值研究

周军勇，苏建旭，齐 飒

(广州大学土木工程学院，广东，广州510006)

车桥耦合振动特性是桥梁在移动车辆荷载作用下结构响应行为的重要表征，不仅可以揭示桥梁结构参数、力学行为和损伤特性[1]，还能反演移动车辆荷载特性[2]，是桥梁工程领域一直以来的研究热点[3-4]。目前，车桥耦合振动的数值研究主要针对确定(有限)车辆荷载工况，发展了针对车桥耦合系统的整体分析和分离迭代等方法[1,4]，针对单元形函数插值的Hermit、Lagrange和样条函数等方法[3]，针对迭代求解的Newmark-β、Wilson-θ和精细积分等方法[1,5]。然而，实际的桥梁结构往往承受时间与空间均高度随机的车流荷载作用，发展随机车流与桥梁耦合振动的数值分析方法具有重要价值，可以提高随机车流作用下桥梁振动响应的评估精度，为在役桥梁的健康诊断与寿命预测提供理论与方法。

随机车流与桥梁耦合振动是在经典车桥耦合理论基础上考虑了车队及其随机特性。Zhang 等[6]较早将车队概念引入车桥耦合动力分析中，研究了自由和拥堵车队作用下桥梁的动力冲击系数与等效均布荷载集度；Cai和Chen[7]建立了随机车流-风-桥的耦合振动系统，研究了车队在横风作用下的车桥耦合特性；韩万水和陈艾荣[8]根据我国实测交通数据，建立了风-随机车流-桥梁空间耦合振动分析模型；李岩等[9]提出一种时变维度的随机车流与桥梁耦合振动分析方法，以提高计算效率。这些研究采用蒙特卡洛抽样方法建立随机车队模型，通过车桥耦合经典理论建立随机车队与桥梁的耦合振动分析方法。然而，基于实测车流数据的蒙特卡洛抽样方法难以真实而高效地反映车队行进过程中的动态演化，例如加速、减速、换道等[9]。因此，O’Brien 和Caprani等[10-11]引入智能驾驶员模型进行车流荷载的微观仿真，仿真结果通过视频车流荷载得到了验证；Chen 和Wu[12]采用元胞自动机交通仿真模型，微观仿真大跨径桥梁车流荷载；Ruan 和Zhou 等[13-15]在文献[12]基础上引入多轴单元胞自动机模型(multi-axle singlecell cellular automaton,MSCA)以改进车流荷载模拟精度，并通过实测WIM数据得到了验证。这些研究提升了实际车流荷载的模拟精度，但主要分析车流静力荷载效应，而未考虑车流与桥梁的耦合动力。

Chen 等[16-17]将元胞自动机微观车流模拟与车桥耦合振动理论进行融合，形成了微观车流与桥梁耦合振动模型，发展了等效动力车轮荷载等简化方法。此后，诸多学者在此基础上研究随机车流与桥梁耦合振动下各类桥型的动力特性和可靠度[18-20]，为运营桥梁的荷载管理和结构评估提供支持。然而，这些研究采用的是经典的N-S随机交通元胞自动机模型(stochastic traffic cellular automaton,STCA)，STCA 模型可以很好地仿真各种交通情形，但其模拟时间步长是1 s，且车辆尺寸及车头间距都是元胞尺寸(通常5 m～7.5 m)的整数倍，这对于桥梁车流荷载的分析难以满足精度需求。Ruan 和Zhou 等[13-15]提出了改进经典N-S模型精度的MSCA 模型，能够适应任意模拟时间步长和精确车辆尺寸和车头间距，但相关研究主要针对静力车流荷载效应。

本文在MSCA 的研究基础上，提出基于元胞自动机微观模拟的随机车流与桥耦合振动理论和方法，充分利用元胞自动机时间与空间均离散、局部规则作用于全局演化、状态更新效率高等优点，实现精细化微观车流与桥梁的高效率动力耦合分析。首先，综述基本车桥耦合振动模型，将“车辆”“路面”和“桥梁”3个子系统进行耦合分析；其次，提出车桥耦合振动分析的MSCA 模型，详细阐述车流演化及车流-桥梁耦合振动的实施过程，并通过MATLAB平台进行程序实现；再则，通过一个连续梁桥的跑车试验数据，验证了本方法在车桥耦合振动分析中的准确性；最后，结合一座大跨径斜拉桥，首先验证了本文所提基于MSCA 的随机车流与桥梁耦合振动分析方法的有效性和准确性，其次阐述了基于本方法进行随机车流激励下的桥梁振动响应分析及结构性能评估的工作展望。

1 车桥耦合振动基本理论

车桥耦合振动理论是将车辆与桥梁两个振动系统通过车桥接触点的力平衡和位移协调建立耦合方程。本文采用半车模型[3]，考虑其沉浮、伸缩和点头三个运动特性，能较准确地反应整体杆系受力特性的桥梁结构在车辆作用下的耦合动力特性。根据虚功原理，半车模型的车辆振动方程如下：

式中：下标v 代表车辆；M、C和K分别代表质量矩阵、阻尼矩阵和刚度矩阵；Z表征运动自由度，对车辆而言包含了各个车轮的竖向位移、车体的竖向位移及纵向转角；Z˙ 和Z¨分别代表运动自由度的一阶和二阶导数，即速度和加速度；Fvb为振动过程中的接触力向量；FGv为车辆在各个自由度的自重向量。

考虑桥梁结构的整体杆系受力特征，车辆作用下的桥梁振动方程如下：

式中：下标b代表桥梁；Z表征自由度，对桥梁而言包含了竖向位移和纵向转角等自由度；Fbv为振动过程中的接触力向量。

车轮与桥面接触需要考虑路面的粗糙度影响，路面粗糙度采用国际标准化协会的ISO SCI/WG4标准，模拟为各态历经的平稳Gauss随机过程，采用功率谱描述路面特性，表达如下：

式中：x为桥梁纵向坐标；k为波数；N为充分大的整数；nk=n0+(k-0.5)Δn且n1＜nk＜n2, Δn=(n2-n1)/N;n0为间断频率，取值1/2π；φ(n0)为桥面不平整度系数，表征极好(A)、好(B)、一般(C)、坏(D)和极坏(E)5种道路平整度级别；n2和n1分别为截止频率的上限和下限。

根据车辆与桥梁在车轮接触点的粗糙度，可以通过位移协调方程建立车桥耦合的振动平衡方程。为提高分析效率，采用模态综合法降低桥梁方程的计算自由度，改写后车桥耦合系统振动方程为：

式中：I为n阶单位矩阵；ω和ξ 分别为桥梁结构频率和阻尼比；Cbv和Kbv分别为经过耦合的阻尼项和刚度项；Φ 为桥梁的模态坐标；Φb为车辆轮胎与桥梁接触位置的模态插值向量；V为车辆的行驶速度；q¨r、q˙r和q r分别为桥梁结构的r阶模态坐标下的加速度、速度和位移向量。

采用分段三次样条函数构造梁单元模型的插值振型函数，将此代入车桥系统耦合方程式(4)，采用Newmark-β 逐步积分法求解系统的动力响应。

2 基于MSCA的随机车流与桥梁耦合振动

2.1 多轴单元胞自动机模型MSCA

元胞自动机将研究对象离散为有限而连续元胞所组成的空间系统，各类参数和信息均存储于元胞状态中，并按照一定的局部规则使得元胞状态在离散的时间尺度上进行演化，从而实现研究系统的动力演化。元胞自动机目前广泛应用于交通微观仿真中，能够根据个体车辆的各类随机状态和选择，进行交通系统的模拟仿真，呈现各种实际可观测的交通情形，是交通微观仿真分析的重要工具[21-22]。Chen 和Wu 首次将元胞自动机引入进行大跨径桥梁微观交通荷载仿真分析[12]，主要采用交通领域广泛应用的N-S随机交通元胞自动机模型，将车辆荷载信息融入模拟中，从而呈现不同交通状态(自由流、拥堵流和堵塞流)的车流荷载信息。然而，N-S模型包含了诸多假定：①单个车辆占据一个元胞；②车辆速度和车头间距都是以元胞整数倍演化；③模拟的时间迭代步长为1 s，这些假定使得车辆与车队的加载精度无法满足桥梁车流荷载的精细化分析需求[10]。针对N-S经典模型无法满足精细化车流荷载模拟需求，Ruan 和Zhou 等[13-15,23]提出多轴单元胞自动机模拟方法，并通过动态称重数据对MSCA 的静力车流模拟效果进行了验证。本文以MSCA 为基础，提出随机车流与桥梁的耦合振动高精度数值计算方法，实现运营车流作用下的桥梁结构响应精细化分析。

在车流与桥梁耦合分析框架中，MSCA 将车辆首轴所占据的元胞定义为有车元胞，其余均为无车元胞，如图1所示，任意有车元胞包含了如下信息：

1)车辆状态参数，表征元胞类型的参数f，f=1和f=0分别代表有车元胞和无车元胞；

2)车辆静力参数，包含首轴所在元胞位置q(0≤q＜1)，轴数k，轴间距p(pi,i=1,2,···,k-1)、前悬of和后悬or；

3)荷载参数信息，车体质量G，车体俯仰惯性矩J，轴重g(gi,i=1,2,···,k)，轮重w(wi,i=1,2,···,k)；

4)车辆动力参数，车轴上层悬挂系统刚度ku(kui,i=1,2,···,k)，车轴上层悬挂系统阻尼cu(cui,i=1,2,···,k)，车轴下层悬挂系统刚度kd(kdi,i=1,2,···,k)，车轴下层悬挂系统阻尼cd(cdi,i=1,2,···,k)；

5)跟车运行信息，当前速度V，车辆间距gapf、gapr,f、gapr,b、gapl,f和gapl,＞b(前后车辆的保险杠距离)；

6)桥梁特征信息，有车元胞左右节点的模态向量nl(nlj,j=1,2,···,M)和nr(nrj,j=1,2,···,M)。

元胞空间、元胞状态、领域和交通规则是元胞自动机的4个基本要素，元胞状态和领域在图1中清晰阐述，元胞空间则是研究对象的总体描述，包含了道路模拟长度l、车道数量n、元胞形状s(矩形)、元胞尺寸Δl、时间步长Δt和道路信息r(包括路面粗糙度函数、是否车道关闭、是否换道限制、是否跟车距离限制、是否限重和是否限速)。交通规则是实现元胞状态变化的驱动力，也是实现车流荷载行进演化的根本算法。

图1 MSCA 元胞状态及领域的图示Fig.1 Diagram of cells'statesand neighborsin MSCA

2.2 基于MSCA 的精细化微观车流模拟

跟驰和换道是交通模拟的两个重要规则，本研究采用STCA 的随机跟驰和随机换道模型进行车流荷载的微观仿真。注意到，MSCA 为了提高车流荷载的加载效率，将时间步长定义为自设定(通常Δt＜1 s)，然而大量研究证明驾驶员的行驶操作反映时间通常都不低于1 s，因此，所有的交通规则定义为基于1 s的单位时间进行演化，但不影响车流荷载的加载步长Δt＜1 s下的演化。根据定义的跟驰和换道规则，动态更新所有元胞的状态。

MSCA 跟驰模型，包含了加速、减速、随机慢化和匀速4个驾驶操作：

1)加速：

图2 MSCA 元胞领域内精细化车流模拟的参数示意图Fig.2 Diagram of critical parameters in the microscopic traffic modeling in the MSCA cell neighbors

MSCA 通过车辆最小间距为准则进行随机换道，当满足如下条件时目标车辆以某一概率换道：

式(10)～式(12)中，各参数如图2所示。一般在中国交通运输环境下，车辆向内侧和外侧车道的换道概率是不同的，需结合特定地点交通状态进行校核确定。

2.3 基于MSCA 的随机车流-桥耦合振动数值分析

目前多数随机车流仿真都是从车辆出发，识别每个车辆在演化过程中的参数，这无疑加大了计算成本。MSCA 改进了随机车流的模拟方式，把关注点从车辆转移到元胞，所有车辆仅以车头元胞呈现，但车辆运动学参数和荷载参数均储备在车头元胞中进行同步演化，通过元胞状态参数的更新来实现整体车流变化，由于桥梁被划分为一系列元胞，在任意时间段下的车流模拟都可以通过有限数量的元胞状态呈现出来，其计算简洁的特点在车流－桥耦合振动研究中十分高效。此外，在MSCA 中车辆可以精细化地以轴加载到桥梁结构，并且车头间距、车速演化都可以根据用户需求进行精度调整。

图3给出了基于MSCA 的随机车流-桥耦合振动数值分析框架，也是进行程序实现的流程。首先，对模拟道路桥梁进行元胞空间初始化，这包括预设基本的道路参数，将路面不平整函数融入元胞空间，同时基于桥梁有限元模态分析结果将插值模态向量及结构模态频率存储进入元胞空间，这些参数在车流模拟演化过程中是恒定的，不随时间变化。其次，根据路段交通荷载统计数据建立车队与车辆的系列生成模型，基于这些数学统计模拟就可以实现任意交通状态的随机车队循环模拟[13,15]。最后，将随机循环产生的车队作用于元胞空间，通过时间的推进，实现车队在桥梁上的动力作用，这包括两个环节：①根据3.2节的微观车流驾驶规则不断作用于行进中的车队，使得车队满足驾驶条件并在桥面随机行驶；②提取每一时刻的有车元胞，将有车元胞中的元胞状态参量组装车流与桥梁的矩阵，实现耦合振动分析，这一细节列述如下：

1)提取t时刻下所有的有车元胞(f=1)，根据车辆静力参数确定桥上车队中所有车轴所在空间位置，并结合车辆静力参数和动力参数构建式(1)所示的车辆振动方程对应的Mv、Cv、Kv和FGv；

2)根据t时刻所有车轴所在位置信息，通过桥梁特征信息获得车轴加载处的模态向量与路面不平度，插值计算加载点的模态位移Φ；

3)计算式(4)中的车桥耦合矩阵Cbv和Kbv等，提取上一时刻桥梁模态位移和有车元胞中的车辆位移，通过Newmark-β 逐步积分法进行求解，存储求解所得桥梁模态位移，更新t时刻有车元胞中储存的车辆位移；

4)对于t+1时刻，再次提取有车元胞，重复操作①②③步骤，直至所有车辆离开桥梁或者达到模拟截止时间，最终获得车与桥的动力效应时程。

3 车桥耦合分析的工程案例验证

采用工程算例进行MSCA 车桥耦合分析的验证。由于车队与桥梁耦合振动的数据较难获取，也不存在理论解答，因此以下通过单车与桥梁耦合振动分析结果进行模型和方法验证，此外MSCA对于车流仿真的准确性和效率已在文献[13,15]进行了详细验证，综合本节验证结果，可以说明MSCA 对车桥耦合振动分析的准确性和精度，具体对于随机车流激励下的桥梁耦合振动将在以下进行验证分析。

基于某三跨连续梁桥的跑车试验结果，验证本文所提出车桥耦合分析方法和模型的准确性。桥梁基本概况如图4所示，为40 m+60 m+40 m 的三跨变截面预应力混凝土连续梁桥，主梁采用C50混凝土，跑车试验采用38 t 三轴整体式载重货车，根据文献[24]对我国车辆动力参数的调研分析，该三轴车的静动力参数如图5所示。

通过对桥梁实地勘测，发现路面已经出现一定程度的退化，路面粗糙度按照“一般”等级进行模拟分析。考虑到桥梁设计图纸与实际施工的差异性，以及桥梁运营使用中可能出现的结构性能退化，根据现场采集的桥梁基频进行结构有限元模型修正，模型修正的基本原则是使得计算模型的基频与实测基频相同。现场采集的桥梁基频为2.138 Hz，为简化有限元模型的更新过程，通过等比例调整桥梁所有材料的弹性模量进行模型修正。图6呈现了不同的混凝土弹性模量对桥梁基频的影响变化关系，发现当材料弹性模量取值3.49×104MPa 时，有限元计算模型的基频为2.147 Hz，与实测基频2.138 Hz 的误差为4.2%，基本满足结构计算的精度要求，尽管可以通过数据内插获得误差更小情况下的混凝土弹性模量，但是2.147 Hz的误差结果已然能够满足精度要求。因此在车桥耦合分析中，以混凝土弹性模量3.49×104MPa 为基础，提取模态向量矩阵，进行车桥耦合动力分析。

图3 基于MSCA 的随机车流与桥梁的耦合分析流程图Fig.3 Flowchart of traffic-bridgeinteraction using MSCA

图4 跑车试验桥梁的立面布置图 /m Fig.4 Vertical layout of the bridge under moving truck test

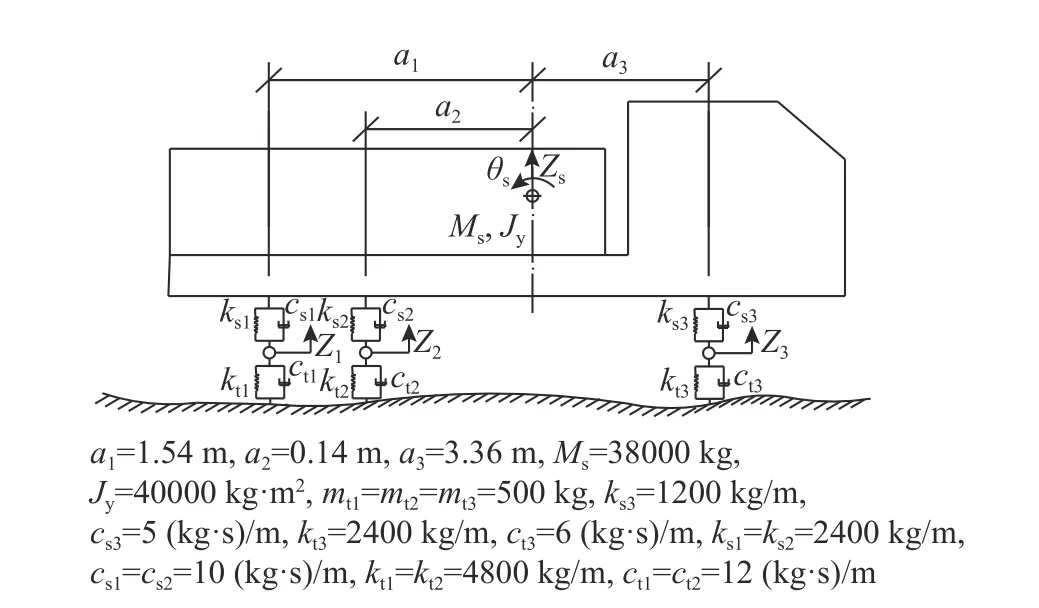
图5 试验用三轴车辆的外形图及静动力参数Fig.5 Layout and static/dynamic parameters of the 3-axle experimental truck

跑车试验采集了38 t 单车以10 km/h、20 km/h和30 km/h 的速度匀速过桥时主梁中跨跨中位移时程，基于此采用本文所提出的模型和方法进行车桥耦合动力分析并提取主梁中跨跨中位移时程，实测值与计算值分别呈现于图7中。总体上程序计算与实测结果具有较好的吻合趋势，最大挠度出现的位置及其数值比较吻合，振动规律基本一致。然而，由于实际跑车试验中司机对速度的控制并不完全规范，会出现通过完试验跨就减速(如图7(a)实测数据衰减迅速)以及跑车过程速度过慢(如图7(c)实测数据更分散)等情况。

进一步将跑车试验中的程序分析及实际采集的跨中最大挠度进行对比，如表1所示。同时通过对采集的实测时程挠度进行十点滑动平均处理(采样频率10 Hz)，得到滤波后的准静态挠度时程，本文方法获得的静态挠度则通过车桥耦合振动方程中剔除动力项的方法迭代计算获得。可以看到理论与实测结果存在最大11.61%的误差，通过滤波处理后的准静态挠度误差只有8.62%，这对于现场工程试验而言是可以接受的，验证了本分析方法的准确性。

4 随机车流-桥耦合分析的工程应用

4.1 分析概述

本节通过一个具体的桥梁案例，利用MSCA进行随机车流与桥梁的耦合振动分析，验证所提模型和方法在随机车流与桥梁耦合振动分析的准确性。案例桥梁是一座双塔双索面钢箱梁斜拉桥，跨径组合为70 m+160 m+448 m+160 m+70 m，桥塔为钻石型混凝土塔柱结构，桥梁设计行车速度100 km/h，采用双向6车道高速公路标准建设，如图8所示。由于本桥采用整体式钢箱主梁结构，汽车荷载在横向不同车道上的作用对主梁挠度影响很小，因此不详述车道荷载响应差异，而只给出结构总体振动响应规律。

元胞空间基本参量定义如表2所示。桥梁位于模拟道路的末端位置，随机减速因子和换道概率根据文献[13]的校核结果取用。

同时，建立该桥梁的三维杆系空间有限元模型，进行模态分析获取该桥梁的前20阶模态数据，如表3所示，输入MSCA 模拟系统中。路面不平整度按照式(3)输入元胞空间中，并根据需求选择道路状况等级。

图6 混凝土弹性模量对桥梁基频的影响关系Fig.6 Influence of theelastic modulusof concrete on the fundamental frequency of the bridge

图7 不同跑车速度下桥梁中跨跨中竖向振动位移的实测与模拟对比Fig.7 Comparison between measurement and simulation of the vertical girder deflection in the mid-span of the bridge subjected to a moving truck at different speeds

结合某收费高速公路采集的双向6车道WIM数据，根据文献[13-15]的方法进行统计分析，获得的车辆与车队参数模型输入到MSCA 中，不同轴型车辆的动力参数参照文献[8]等结果，根据图3编制的MATLAB程序进行随机车流与桥梁的耦合动力分析，获得随机车流作用下的桥梁振动响应时程。模拟了双向6车道46000 veh/d 的交通流量，关于该组WIM 数据的统计特性，请查阅文献[25]中地点2的车辆荷载分析结果，限于篇幅这里仅给出两个行车方向的时均交通流量变化规律及时均货车比例，如图9所示。两个行车方向都呈现两个峰值交通量(即上午和下午)，日间交通流量远大于夜间，但是夜间货车比例很大，最大达到了80%，而日间货车比例只有25%左右。这种日夜间的交通流及货车比例特点，反映了我国高速公路夜间重载交通的行驶特点，这是我国高速公路的典型运输情况。

图9 WIM 数据的交通流时变特性Fig.9 Thetime-varying characteristicsof WIM data

4.2 随机车流与桥梁耦合振动的验证分析

目前还没有可供随机车流与桥梁耦合动力分析验证的基准模型和数据，主要是因为：一方面，实测车流作用下的桥梁动力响应获取较为简单，但是与之对应的过桥随机车流在时间和空间上的复杂演化历程还难以准确采集；另一方面，模拟车流本身由于高度的随机性难以完全重现，因此也无法提供数值解唯一的基准模型。已有的随机车流与桥梁耦合振动分析方法，主要根据其动力计算结果与静力计算结果(或工程判断)的一致性进行验证[7-9]。基于此，本节将随机车流与桥梁耦合振动分析的动力效应和静力效应进行对比，间接验证本文所提方法和模型在随机车流与桥梁耦合振动分析方面的准确性与精度。

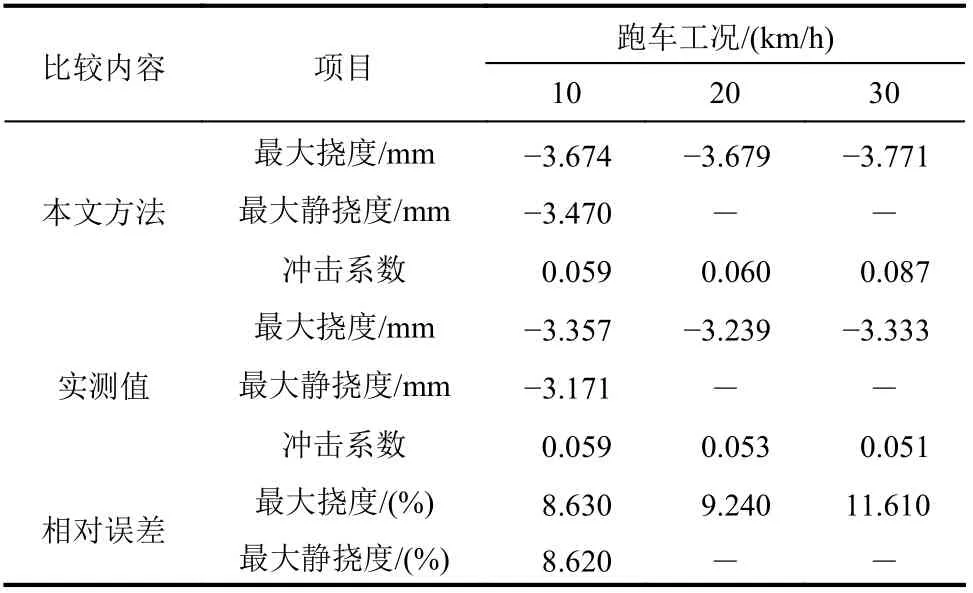
表1 不同车速下桥梁跨中竖向位移的理论与实测对比Table 1 Comparison of themid-span vertical displacements between theoretical calculation and experimental testing subjected to a moving truck with different speeds

表2 MSCA 输入参数的取值列表Table 2 A list of input parametersin MSCA

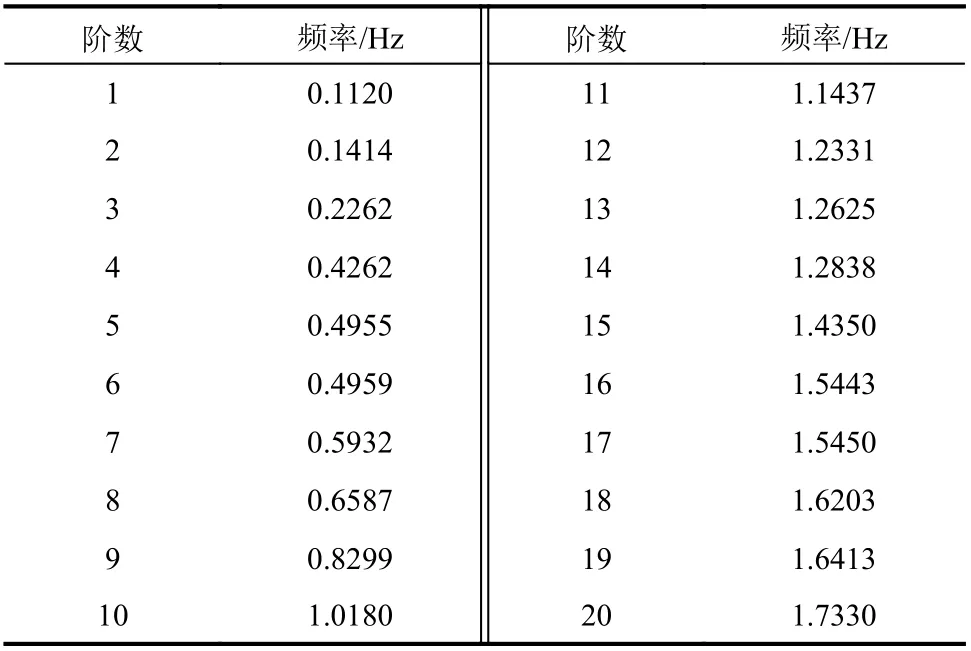
表3 桥梁有限元分析的前20阶频率特性Table 3 The first 20 natural frequencies based on finite element analysis of the bridge

图8 斜拉桥的立面布置图 /m Fig.8 Vertical layout of the cable-stayed bridge

分别考虑路面不平度为A 级、C级和E 级情况下随机车流激励桥梁的振动响应。选取了随机车流运行10 min 的主梁中跨跨中振动位移时程，同时提取该随机车流作用下的静态位移时程(静态效应通过剔除式4中的动力项获得)，结果比较如图10所示。当路面粗糙度等级为A 级时(图10(a))，结构的振动响应不显著，动力时程挠度与静力时程挠度基本吻合，在局部区域动力时程挠度存在一定程度的振荡，但是振荡误差非常小。当路面粗糙度等级为C 级时(图10(b))，结构振动响应较为明显，但仍然可以看出动力效应与静力效应时程规律基本一致，在最大挠度位置的静力效应与动力效应的误差不超过10%。当路面粗糙度等级为E 级时(图10(c))，结构振动响应非常显著，振动挠度甚至达到静力挠度的2倍～4倍，但是从时程走势来看，振动挠度与静挠度的走势规律基本一致。这些比较说明，本文所提出的基于MSCA的随机车流与桥梁耦合振动分析方法和模型，可以准确反映大跨径桥梁在随机交通激励下的振动响应特性。

图10 不同路面等级下桥梁的振动位移比较Fig.10 Comparison of girder vibration deflections under different road roughness levels

4.3 随机车流下结构振动挠度

结合前述验证，可以采用本方法和程序模拟任意周期和交通参数下的随机车流与桥梁耦合振动效应。图11(a)是某一天获得的随机车流作用下案例桥梁中跨跨中位置主梁振动位移时程效应，由于该桥是重要跨海通道因此路面等级考虑为C级，时程挠度可知静动力挠度具有相同走势的时程曲线，但是动力挠度在局部区域要显著大于静挠度；此外该位置的主梁基本处于下挠状态，最大下挠位移达到了10 cm，而最大上挠位移仅仅不到2 cm。日间交通流量大因此时程挠度均值要显著大于夜间的，但是从最大挠度来看，夜间与日间相差不大，主要原因是夜间虽然交通流量小但是货车平均载重要更高(图9(b))。

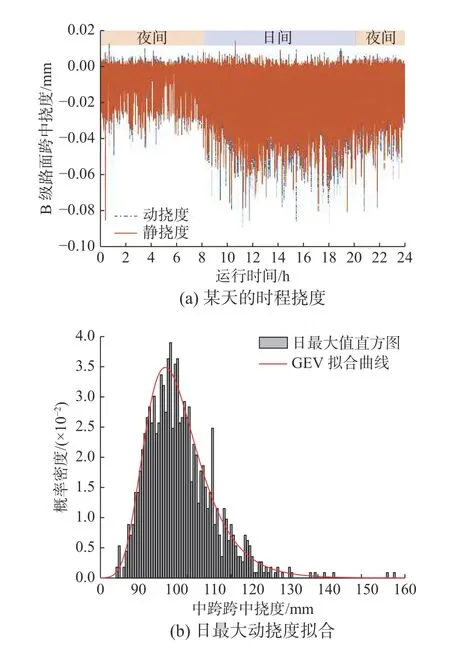
图11 随机车流作用下中跨跨中主梁时程动挠度分析及日最大值GEV 拟合Fig.11 Time-history analysis and block maxima GEV fitting of mid-span girder dynamic deflections under random traffic excitation

图11(b)是模拟了90 d 时程挠度数据获得的日最大动挠度效应的概率密度直方图，并对直方图分布进行广义极值分布(generalized extreme value distribution,GEV)拟合。可以看到，最大值样本基本服从GEV 分布，拟合效果较好，基于此可以建立桥梁在随机车流作用下的极值挠度分布模型，用于评估该桥梁在随机车流激励下因桥梁变形引起的行车舒适性是否满足运营需求，这将是课题研究的后续工作，限于文章篇幅不做详细介绍。

5 结论

本文将经典车桥耦合振动理论融入最新提出的多轴单元胞自动机(MSCA)微观车流荷载模拟方法中，形成了一种精细化的随机车流与桥梁耦合振动数值分析方法；对该数值方法进行了程序实现，并通过工程算例进行了程序验证；最后将该数值分析方法应用于某斜拉桥的动力分析中。本文主要结论及展望如下：

测试了某连续梁桥跑车试验的动态挠度时程，并与MSCA 数值分析结果进行对比，两者具有高度的一致性，尽管由于实桥试验受到各种因素影响，理论与测试结果具有一定的误差(最大达11.6%)。该工程算例证明了MSCA 进行车桥耦合动力分析的准确性，由于MSCA 开展静态车流的精度和效率已在先前研究中验证，因此MSCA 可以用于随机车流激励下的桥梁各类动力效应分析中。

将MSCA 用于某斜拉桥的动力挠度分析中，计算了各种路面粗糙度下的随机车流激励桥梁产生的动力和静力挠度时程，分析两者具有很好的一致性，随着路面粗糙度等级提升两者差异更加显著，这些证明了本模型和方法在开展随机车流与桥梁耦合振动分析的可靠性。

已有研究证明了MSCA 能高效率高精度地仿真随机车流在桥梁上的微观动态加载作用。本研究将MSCA 与经典车桥耦合振动理论进行融合，拓展了MSCA 在随机车流激励下分析桥梁动态响应的能力，可以用于各类复杂交通场景下的桥梁结构可靠性评估，为量化高度随机的交通荷载对桥梁的作用效应，提供了高效分析工具。限于文章篇幅，后续研究可以进一步将MSCA 与桥梁健康监测系统进行融合，实现桥梁车辆荷载的实时在线评估与管理。