基于敏感性分析的协方差随机子空间方法参数优化
2021-03-02刘威,杨娜,2,白凡,2,常鹏,2
刘 威,杨 娜,2,白 凡,2,常 鹏,2
(1.北京交通大学土木建筑工程学院,北京100044;2.结构风工程与城市风环境北京市重点实验室,北京100044)
对于大型工程结构,通过环境激励[1-3]的工作模态分析(operational modal analysis,OMA)既能确保结构的安全,还能降低维护和管理的成本[4]。通常将环境激励视为平稳白噪声,基于这一信号输入假定以及线性结构分析的前提,可仅通过输出响应进行结构模态识别。在众多时、频域识别方法中,随机子空间法(stochastic subspace identification,SSI)属于现代谱分析的范畴,为参数化的计算方法,凭借较强的鲁棒性和有效性而被广泛使用[5]。
基于统计概率意义的多维数据模态分析,SSI具有同时处理多维数据特点[6]。由于其直接利用测试得到的响应数据构建计算结构模态参数的矩阵,避免了传统的模态识别方法中采用傅里叶变换造成的谱泄漏等问题。识别过程中根据算法不同可分为数据驱动随机子空间(data-driven stochastic subspace identification,SSI-Data)及协方差驱动随机子空间(covariance-driven stochastic subspace identification,SSI-Cov)。由于前者涉及投影矩阵的计算,计算效率较低,因此本文选择SSI-Cov进行研究。
SSI-Cov 中涉及一些重要参数,如系统阶数N、Hankel 矩阵中过去输出子矩阵的行块数g和未来输出子矩阵行块数h、Toeplitz 矩阵的行块数i和列块数j等[7]。其识别模态参数的精度不仅取决于环境因素的影响,还依赖于人为选择参数的合理性[8]。合理的参数选择是准确识别结构模态的前提[9],而准确识别结构的模态对于结构的健康监测及损伤评估至关重要。


因此,对相关参数进行敏感性分析以及提出建议取值对模态参数的准确识别具有重要意义。此外,目前关于利用SSI-Cov 对藏式古城墙进行模态识别的研究相对匮乏,并且用于SSI-Cov 的参数选择研究更是鲜有报道。本文基于敏感性分析,结合一经典数值算例分析了系统阶数N及Toeplitz 矩阵行块数i对模态识别过程中稳定图及计算结果的影响规律。提出在利用SSI-Cov进行模态识别过程中,可引入奇异熵增量理论确定系统阶数N,并给出i的建议取值范围。最后根据藏式古城墙模态识别的应用,说明了本文所研究的参数优化方法可准确识别结构的动力特性。
1 协方差随机子空间算法
SSI-Cov 基于随机状态空间模型[6],首先将响应数据表达为Hankel矩阵,然后通过计算响应数据的协方差序列组成Toeplitz 矩阵,最后通过对Toeplitz 矩阵进行奇异值分解和特征值分解得到系统矩阵,从而完成结构的模态参数识别。
Hankel 矩阵定义为:

对于离散系统,最终只需要求出系统矩阵A及输出矩阵C即可完成模态参数的识别,其中C为 Γi的前l行。
模态参数识别过程中,稳定图法广泛应用于真假模态的鉴别。由于实际工程结构的系统阶数往往未知,因此通常假定系统阶数为Nmin至Nmax。系统的特征值两两共轭,阶数必须为偶数。通过将计算结果绘制在二维坐标图上(横轴为频率、纵轴为系统阶数),从而形成稳定图[14]。其中,对于相邻系统阶数为2n和2n+2下的识别结果,需要进行稳定准则(式10(a)~式10(c))判断,只有满足稳定准则的模态结果才绘制在稳定图上。

式中:H为Hermit 转置;MAC为模态置信因子[11]。
2 数值模型
为了研究SSI-Cov 的关键参数对模态识别的影响,基于MATLAB语言设计程序,通过参考相关算例[15]建立一个5自由度质量-弹簧-阻尼系统的数值模型(如图1所示)。

图1 5自由度质量-弹簧-阻尼系统模型Fig.1 A 5-DOFmass-spring-dashpot system
模型中每个单元质量、刚度、阻尼系数分别为:mn=50 kg,kn=2.9×107N/m,cn=1000(N·s)/m。通过特征值分析,模型前5阶频率、阻尼比以及振型系数理论值分别,如表1、表2所示。

表1 模型理论频率和阻尼比Table 1 Theoretical values of model frequency and damping ratio
利用MATLAB对首个质量块m1输入高斯白噪声激励,采样频率700 Hz,采样时间50 s,各通道采集的数据长度为35 000。提取各质量块输出信号如图2所示。

表2 模型理论模态振型Table 2 Theoretical value of modal shape of the model

图2 白噪声下各质量块输出信号Fig.2 Output signal of each massblock under whitenoise
3 SSI-Cov 算法的模型修正及参数优化
利用SSI-Cov 进行系统识别时,是基于构建的数学模型与测量数据的拟合,以提取未知的模型参数。通过对Toeplitz 矩阵T1|i进行奇异值分解以及对系统矩阵A进行特征值分解,从而完成未知模型参数的计算。
在利用SSI-Cov 进行模态识别涉及的参数中,j应趋于无穷大,然而由于测试数据长度不可能为无限,为充分利用所测试数据,设数据总长度为s,则可得:

在对li×li维的矩阵T1|i进行奇异值分解时可知i与N在算法上需要满足以下关系:

由式(12)可知,当系统阶数N确定时,i的选择存在一个下限值。但实际应用中,当结构基频f0相对于采样频率fs较低情况下,此时i又设置的较小时,会使得Hankel块矩阵中的输出协方差数据信息不全,从而导致部分模态信息的缺失。因此,Reynders[16]通过不确定性分析给出了i的建议值,令 β=fs/f0,则:

本文主要针对N、i这两个自定义参数的选择对计算精度的影响展开分析。由于在对Toeplitz 矩阵进行奇异值分解以及对系统矩阵进行特征值分解过程中涉及到逆问题的求解,故引入条件数κ来衡量数值误差对识别精度的影响:

式 中,λ1、λN分 别为Toeplitz 矩阵T1|i(系统 矩阵A)中的第1个和第N个奇异值。
根据稳定图的工作原理,为了准确量化模态识别的稳定性,通过计算识别结果中频率(阻尼比)的总变异系数δF|D作为评价指标:
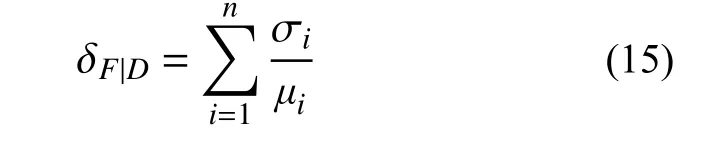
式中:n为目标识别模态的阶数; σi、μi分别对应第i阶模态在Nmax阶下计算结果的标准差和均值。
3.1 系统阶数N
本数值模型中,目标识别模态为系统的前5阶,即n=5;理论系统阶数为10。为分析参数N对识别结果的影响,结合式(13)暂取i=3β ≈60,j=s-2i+1=34881。
由于噪声的影响不可避免,使得高阶的原本等于零的奇异值不完全等于零,从而无法直接通过对Toeplitz 矩阵进行奇异值分解确定系统阶数。在使用稳定图方法时,要先假设一个较大的系统阶数N,N的选取是否合理,直接影响稳定图的效果:取值偏大,导致稳定图中出现较多虚假模态;取值较小,则发生系统真实模态遗漏。因此,设置最大系统阶数为Nmax∈[6,42],且公差为4的等差序列。
图3~图5分别给出了在不同系统阶数下(N=10、26、42)识别结果的稳定图、条件数及相应的变异系数。其中,对于该数值算例,频率识别精度相对较高,故仅针对阻尼比变异系数进行比较;另外,为了分析计算精度与变异系数之间的关系,同时在图5中加入阻尼比总误差,即所识别的各阶阻尼比与理论值的绝对误差的平均值,其中所识别的各阶阻尼比是指稳定图各极轴中对应阻尼比的平均值。

图3 不同系统阶数下的稳定图Fig.3 Stability diagrams at different system orders
由图3可知:随着系统阶数的增大,频率稳定极轴逐渐出现数学虚假模态的干扰。部分可能的模态与数学模态相关联而围绕在物理极点附近形成新的极轴,从而给各阶模态的准确识别带来困难。当N=10,即等于理论系统阶数时,可以发现系统的前5阶模态均很好的识别,并且无数学模态出现。
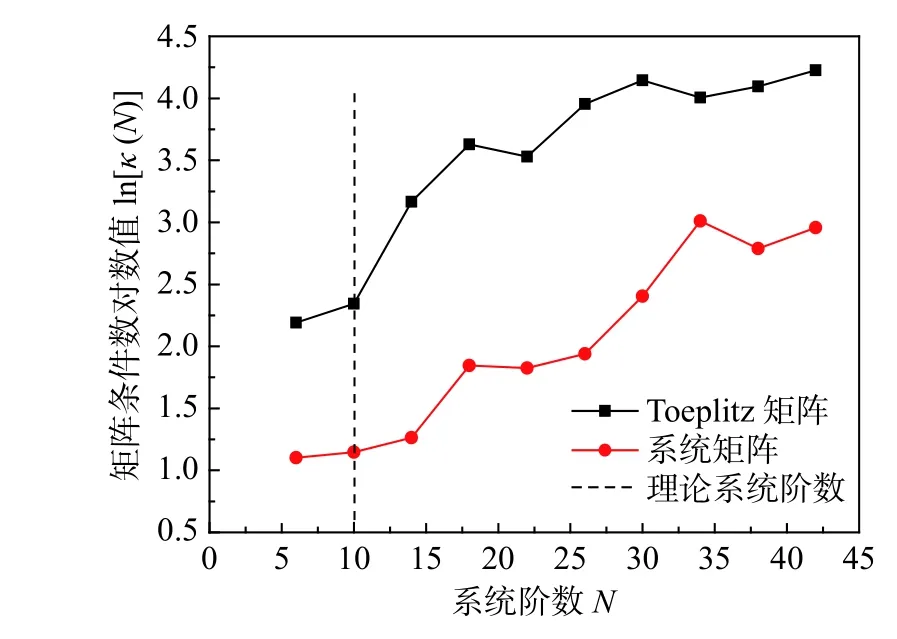
图4 条件数随系统阶数的变化规律Fig.4 Variation law of condition number with system order

图5 阻尼比识别结果变异系数及平均误差Fig.5 Coefficient of variation and average error of damping ratio recognition results
条件数反映了逆问题求解过程中线性方程组的病态与否。当条件数越小,求解精度越高,响应数据的扰动对系统的扰动越小。图4给出了Toeplitz 矩阵以及系统矩阵A的条件数随系统阶数的变化规律,可以发现二者均随N的增大而增大,整体呈正相关关系。
图5根据式(15)计算了阻尼比在不同系统阶数时的总体变异系数:当N<26时,总变异系数及平均误差均维持在相对较低的水平;当N>26时,阻尼比变异系数急剧增大,平均误差也越来越大。二者表现出一定的相关性,原因在于变异系数反映了不同系统阶数下模态识别结果的稳定性,当变异系数值较大时,往往对应于稳定图中出现较多的数学极点干扰,从而影响模态识别精度,造成较大误差。另外,当N=6时,第4和第5阶模态出现遗漏,原因在于系统阶数太低(低于真实系统阶数)。
为了对系统阶数进行准确识别,本文通过引入奇异熵增量理论来确定N。首先,奇异谱表示的是各个状态变量在整个系统中所占能量的相对关系;而熵是一切事物状态不确定性的度量,信息熵是考察信号包含信息量的有效指标之一[17-19];因此,奇异熵对信号信噪比的变化反映非常敏感,可用于系统阶数的识别。
假定系统有m个状态,每个状态存在的概率为pi,则该系统的熵E可表示为:

在无噪声或高信噪比情况下,通过对Toeplitz矩阵进行奇异值分解得到其特征值对角矩阵为:

式中,k为奇异熵的阶数,k≤N。ΔEi表示奇异熵在阶数i处的增量,其表达式为:

当奇异熵增量降低到渐近值时,信号的有效特征信息量才算基本完整;此时,对于同一信号,不论其信噪比高低,对应的奇异谱阶数完全相同。基于奇异熵这一特性,当奇异熵增量趋于稳定时,所对应的奇异谱阶数即可认为是系统阶数。
随着系统阶数的增大,对于指定的一个系统,不同N值下的奇异熵增量计算结果相同。以N=10、26、42为例,截取计算结果的前30阶进行绘图,该系统奇异熵增量均如图6所示。在实际工程应用中,通过对奇异熵计算一阶灵敏度可以进一步直观的观察系统阶数。由图6可知,当N=10时,奇异熵增量的一阶灵敏度降低为0,即该数值模型的系统阶数为10,结果与理论值一致。
3.2 Toeplitz 矩阵行块数i

图6 奇异熵增量及其一阶灵敏度Fig.6 Singular entropy increment and its first-order sensitivity
结合式(12)、式(13)可知,当系统阶数N确定,i≥max(N/l,0.5β)。即便如此,对于参数i,仅可以得到其下限值,并没有确保子空间模型和响应数据拟合更优、稳定图更清晰的取值范围,而i的取值对计算结果和稳定图的影响不可忽视[20]。因此,在数值模型和实际应用中,首先基于奇异熵理论确定系统阶数N,然后通过分析i的取值对Toeplitz 矩阵T1|i(系统矩阵A)的条件数以及稳定图识别质量的影响,分析其最优化取值区间。
根据数值算例,取N=10,i=[β:0.5β:5β]。图7反映了不同i值对条件数的影响,即在β ~5β,Toeplitz 矩阵T1|i(系统矩阵A)的条件数对i的取值不敏感,整体波动较小。i=β 、 3β 、 5β时的稳定图结果如图8所示。当i>4β时,由于i的取值过大而导致第5阶模态在稳定图上出现遗漏的现象(如图8(c)所示)。由于该5自由度数值模型系统阶数较小,仅为10阶,所以在实际绘制稳定图时N的取值也可适当大于基于奇异熵识别的系统阶数。

图7 条件数随i 值的变化规律Fig.7 Variation law of condition number with i value

图8 不同i 值下的稳定图Fig.8 Stability diagramsat different valuesof i
图9给出了阻尼比在不同i值下的变异系数及平均绝对误差。由图可知:识别的前5阶目标阻尼比的变异系数在i=β~2β时逐渐增大,在i=4β~5β时逐渐减小,在i=2β~4β时呈现先减后增的趋势。结合平均绝对误差先减小后增大的规律可得:当i=2β~4β时,阻尼比变异系数和平均绝对误差均相对较小。其中,i=3β时阻尼比的变异系数最小,为0.89%,前5阶阻尼比平均绝对误差为8.75%,前5阶理论与识别的振型MAC值分别为1、1、0.994、0.996、0.993。因此,基于数值算例分析可得:当i=2β~4β时,模态识别的精度较高。

图9 阻尼比识别结果的变异系数及平均误差Fig.9 Coefficient of variation and average error of damping ratio recognition results
4 应用
4.1 现场测试
4.1.1结构概况
本文研究的藏式古城墙为西藏地区某典型古城墙。该城墙被门楼、塔楼分为5段。由于墙体周边地面有起伏,从不同位置测量高度有差异,各段高度为6.0 m~6.9 m(不考虑女儿墙高度)。底部厚度为4.2 m~5.8 m,顶部为3.1 m~3.8 m。
古城墙原为夯土墙,夯土中掺入了卵砾石,后来先后在城墙内外立面各增加一层0.5 m 厚的石砌体。墙体采用收分设计,高大厚重,两侧的石砌体为方石叠压片石的结构,沿石砌体墙面不同高度处还不规则的设置了透气孔。根据上述建造工艺,从而形成了藏式传统古城墙独特的建筑风格。然而经历数个世纪的自然灾害洗礼,古城墙局部出现了较严重的病害,如东墙北段曾发生大面积坍塌,如图10所示。

图10 E 段墙发生坍塌Fig.10 Collapse of section E wall
4.1.2环境激励测试方案
对于城墙结构,振动主要体现为平面外振动。为了获取其平面外振动特性,从而了解各段墙体的模态信息,具体包括结构频率、阻尼比、振型。根据结构特点以及测试条件限制,按照图11所示的截面(A1~E2)分别对5段城墙进行加速度信号动力测试,截面选取原则为:1)对于较短的墙A、D,选择跨中作为测试截面;2)对于较长的墙B、C、E,选择近似三分点处;3)考虑墙体中部透气孔分布的随机性。

图11 城墙测试截面示意图/m Fig.11 Schematic diagram of the test section of the city wall
为避免对城墙结构造成影响和破坏,采用环境激励法进行动力测试。测点布置原则为:1)结合城墙结构分布有透气孔这一特点,各测试截面按照内侧墙底、内侧墙中、内侧墙顶、外侧墙顶、外侧墙底分别布置5个测点(如图12);2)其中内侧墙中测点优先选在1/2高处,实际布置高度均予以测量;3)测点方向布置为朝墙体内侧方向,即南墙传感器方向均为由南向北,东(西)墙传感器方向均为由东(西)向西(东)。各测点传感器通过快干粉固定并调至水平。

图12 墙体透气孔分布及传感器布置情况Fig.12 Distribution of air permeability holesin wallsand arrangement of sensors
测试设备如图13所示:数据采集设备为北京东方所INV3062T 四通道采集仪,测试时最多需要3台采集仪同时工作(对于A、D两段墙为5通道,B、C、E三段墙为10通道);传感器为941B型超低频加速度测振仪,内置前置放大器功能。采样频率为128 Hz,采样时长为50 min,每个测点采集加速度数据总量为384000个。测试过程中,确保附近无其他干扰激励源。

图13 现场测试设备Fig.13 Field test equipment
4.2 模态识别与参数分析
4.2.1系统阶数N的确定
本文以E段墙为例,进行其模态参数的识别。主要针对古城墙面外振动的前3阶模态进行识别,即n=3。根据频域谱分析可知,结构基频约为6 Hz。为分析参数N对识别结果的影响,结合3.1节的分析结果先选定i=3β ≈66,j=s-2i+1=383869,设置最大系统阶数为Nmax∈[18,58],且公差为4的等差序列。
图14给出了N=22、38、54时的稳定图识别结果。可以看出:随着系统阶数的增大,SSI-Cov识别的稳定图中数学模态随之而增多。对于识别的前3阶目标模态,当N=22时物理极轴相对稳定,干扰最小;N=38时,第3阶模态附近开始出现数学模态的极点;N=54时,第1阶和第3阶模态周围出现较多的数学模态形成的极轴。
图15、图16分别为不同系统阶数下,条件数及变异系数变化规律:1)Toeplitz矩阵及系统矩阵A的条件数随系统阶数的增大近似呈线性增大;2)识别结果中阻尼比的变异系数明显比频率大,且阻尼比变异系数随系统阶数的变化波动较大,而频率变异性很小。
根据3.1节奇异熵理论,识别藏式古城墙的E 段墙的系统阶数:该结构奇异熵增量及其一阶灵敏度如图17所示,当N在22附近时,奇异熵增量一阶灵敏度趋于0,因此识别出该系统阶数为22。结合图14(a),同时也说明了当系统阶数设置的越接近实际值,基于SSI-Cov 方法识别的稳定图越稳定。
4.2.2 Toeplitz 矩阵行块数i的选择
已知藏式古城墙面外振动系统阶数N=22,取i=[β:0.5β:5β]。图18反映了不同i值对条件数的影响,与数值算例不同的是:在 β ~5β,Toeplitz矩阵T1|i(系统矩阵A)的条件数随i的增大而减小,且减小速率逐渐变缓。频率和阻尼比的变异系数在2β <i<4β时变化趋势相对平缓,随后急剧增长(图19)。i=β 、3 β 、5 β时的稳定图结果如图20所示。当i=β时,第2阶模态在稳定图上出现遗漏的现象(图20(a));当i=5β时,第2阶模态周围出现数学模态干扰。综合来看,当i=2β~4β时,既能得到清晰的稳定图,又能满足识别结果的数值稳定性,i的建议取值范围与算例结论一致。

图14 不同系统阶数下的稳定图Fig.14 Stability diagrams at different system orders

图15 条件数随系统阶数的变化规律Fig.15 Variation law of condition number with system order

图16 频率、阻尼比变异系数随系统阶数的变化规律Fig.16 Variation law of variation coefficientsof frequency and damping ratio with different system orders

图17 奇异熵增量及其一阶灵敏度Fig.17 Singular entropy increment and itsfirst-order sensitivity
4.2.3模态识别结果
根据上述系统阶数及Toeplitz 矩阵行块数的选择分析,再次验证了基于奇异熵理论确定系统阶数N,且i选择为2β~4β时,可更好地识别结构的模态参数。文中针对藏式古城墙结构最终选择N=22,i= 3β进行模态识别。表3给出了E段墙的前3阶频率和阻尼比信息。由于各段城墙两端均连接着角楼或者门楼,故假定各段城墙两端为固接。由于E段墙沿高度方向布置了上、中、下3处测点,沿长度方向布置了两处截面,故仅将前两阶振型绘制如图21所示。
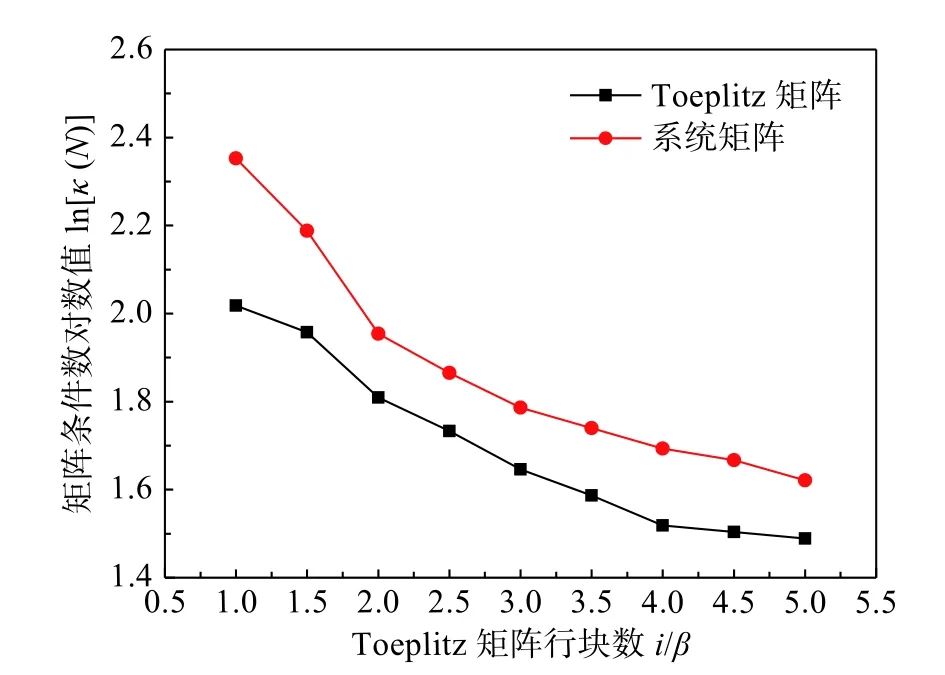
图18 条件数随i 值的变化规律Fig.18 Variation law of condition number with i value

图19 频率、阻尼比变异系数随i 值的变化规律Fig.19 Variation law of variation coefficient of frequency and damping ratio with i value


图20 不同i 值下的稳定图Fig.20 Stability diagramsat different valuesof i

表3 E 段墙面外振动前3阶模态参数Table 3 The first third-order modal parametersof external vibration of section Ewall

图21 E 段墙面外振动模态识别结果Fig.21 Modal recognition results of out-of-plane vibration of section Ewall
根据图21可知,E 段城墙面外振动的一阶振型中两截面振动方向相同,截面E1、E2均近似为弯曲型;二阶振型中两截面振动方向相反,截面E1、E2均为弯曲型,此时沿墙体纵向发生一定程度扭转变形。
5 结论
本文通过对协方差驱动随机子空间法中的几个参数优化进行敏感性分析,重点研究了系统阶数N及Toeplitz 矩阵行块数i对模态识别过程中稳定图及计算结果的影响规律。首先,结合Toeplitz矩阵和系统矩阵的条件数分析计算模态结果的精度;然后,基于模态参数识别结果的变异系数分析其与稳定图质量的关系。利用一经典数值算例(五自由度质量-弹簧-阻尼结构)进行了验证,进而应用于藏式古城墙结构模态参数的现场实测。主要结论如下:
(1)Toeplitz 矩阵或系统矩阵A的条件数越小计算结果精度越高;识别频率、阻尼比的变异系数越小,对应的模态稳定图质量越好。
(2)通过奇异熵增量理论可准确识别结构的系统阶数N,奇异熵增量的一阶灵敏度降至0时对应的阶数即为系统阶数。
(3)协方差驱动随机子空间法中,Toeplitz 矩阵行块数i的建议取值范围为2β~4β ( β为采样频率与结构基频的比值)。
(4)基于本文提出的参数优化方法,利用协方差随机子空间法能有效识别藏式古城墙的动力特性,包括频率、振型和阻尼比:识别该结构的前3阶频率分别为5.93 Hz、7.80 Hz、11.15 Hz;前3阶阻尼比分别为0.0238、0.0364、0.0479。
